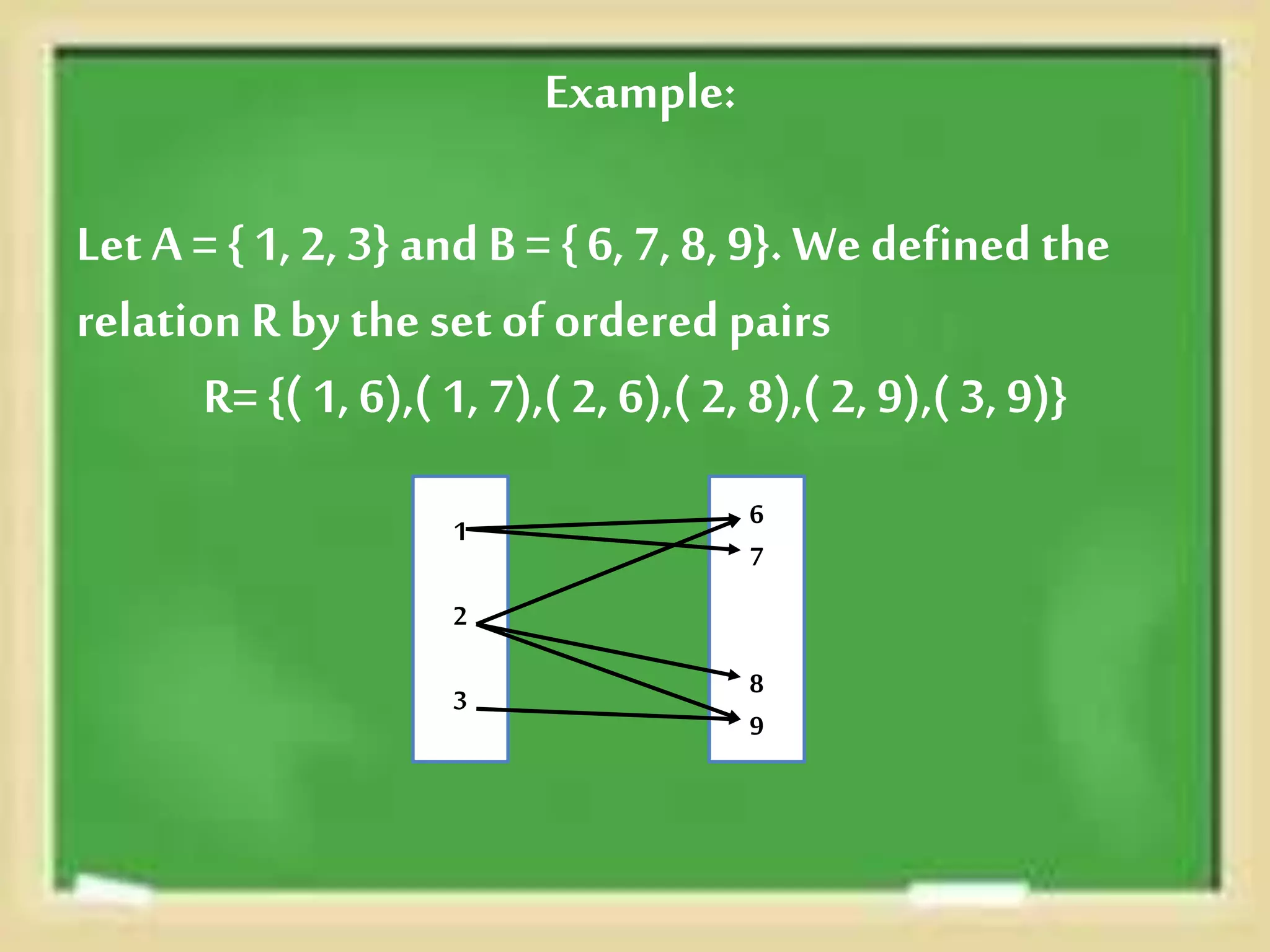
A relation is a set of ordered pairs that shows a relationship between elements of two sets. An ordered pair connects an element from one set to an element of another set. The domain of a relation is the set of first elements of each ordered pair, while the range is the set of second elements. Relations can be represented visually using arrow diagrams or directed graphs to show the connections between elements of different sets defined by the relation.

1. RELATIONS
PearlRoseCajenta
REPORTER

2. What is a 'relation'?
In math, a relation is just a set of
ordered pairs.
- is a pair of numbers used to
locate a point on a coordinate plane;
the first number tells how far to move
horizontally and the second number
tells how far to move vertically.
*OrderedPair
*Set
- is a collection.

3. Note:
{ } are the symbol for "set“
Some Examples of Relations include:
{ (0,1) , (55,22), (3,-50) }
{ (0, 1) , (5, 2), (-3, 9) }
{ (-1,7) , (1, 7), (33, 7), (32, 7) }

4. Given a sets A and B, a binary relation from A to
B is a set of ordered pairs (a,b), whose entries a ϵ
A and b ϵ B. Each orderedpair (a,b) in a
relation is a memberof the Cartesian set A x
B. Hence,arelation from A to B is a
subset of A x B.
Clickfor some Examples

5. Domain and Range of a
‘Relation’
The Domain:
Is the set of all the first numbers of the ordered
pairs.In other words, the domain is all of the x-
values.
The Range:
Is the set of the second numbers in each pair,
or the y-values

6. Example 1:
of the Domain and Range
RELATION {(0,1) , (3,22) , (90, 34)}
Domain : 0 3 90
Range: 1 22 34

7. Example 2:
Domain and rangeof a relation
RELATION {(2,-5) , (4,31) , (11, -11), (-
21,3)}
Domain: 2 4 11 -21
Range: -5 31 -11 3

8. Example3
What is the domain and range of the followingrelation?
ANSWER:

9. Arrow Diagram
-is use by describingthe
relationfrom A into B sets.

10. Example:
Let A = { 1, 2, 3} and B = { 6, 7, 8, 9}. We defined the
relationR by the set of orderedpairs
R= {( 1, 6),( 1, 7),( 2, 6),( 2, 8),( 2, 9),( 3, 9)}
1
2
3
6
7
8
9

11. DirectedGraph
Is a set of vertices and a collection
of directed edges that each
connects an ordered pair of
vertices.

12. Let A = {1,2,3}. Let R be the relationdefined by the
followingsets.
R= { (1,1), (1,2), (2,1),(3,1), (3,3)}
Let us construct the digraphof the relation.
3
1 2
NEXT

14. Examples
1.We can take the set A of students and the set
B of programs. We Can relate the elements of A
to the elements of B by defining that an element a
of A is related to an element b of B if a takes b.
A= { Beth, Mita, Recca, Jean}
B={Computer Science, Information Technology,
Information Science, Civil Engineering}
Answer:
R={(Beth,ComputerScience),(Mita,InformationTechn
ology),(Recca,InformationScience),(Jean,Civil
Engeneering)
More Examples

15. Let A = {1,2,3,}, then each of the following is a
relation in A:
R1 ={(a,b)| a < b} = {(1,2),(1,3),(2,3)}
R2={(a,b)| a = b} = {(1,1),(2,2),(3,3)}
R3={(a,b)| a > b} = {(2,1),(3,1),(3,2)}
R4 ={(a,b)| a + b =4} = {(1,3),(2,2),(3,1)}
R5={(a,b)| b = 4a} = 0
R6={(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),
(3,2),(3,3)}
R2 is called the identity relation. R5 is called trivial
relation or void relation or empty relation. The
universal relation on a set consist of all possible
ordered pairs of elements of a set, example is R6.
NEXT

17. 2. Let A = {1,2,3,4} and B = {u,v,w}, Let
R = {(1,u),(2,u),(3,v),(4,w)}
Then R is a subset of A x B so R is a relation from
A to B. Notice 1Ru but 3R u.
3.Let A = {1,2,3,4} and B = {1,2 ,3,4}, where R is a
relation from A to B defined by a|b, “a divides b,
(a,b) ϵ R. We see that
R = {(1,1),(1,2),(1,3),(1,4),(2,2),(2,4),(3,3),(4,4)}
NEXT

18. Let A={ 1, 3 } and B= { 2, 5 }. Then we
ask how elements in A are related to
elements in B via the inequality `` ''.
The answer is
1 2,1 5, 3 2, 3 5 .
R= { (1, 2), (1, 5), (3 ,5) } ,
NEXT

19. Let A ={ 1,2} and B={ 1,2,3} and define a binary
relation R from A to B by for any (x,y) AxB: (x,y)
R iff x-y is even
(a) Give R by its explicit elements.
(b) Is 1R1 ? Is 2R3 ? Is 1R3 ?
Solution
(a) For any (x,y) pair in AXB ={ (1,1), (1,2), (1,3),
(2,1), (2,2), (2,3) }, we must check if xRy or if x-y
is even. This is done in the following table
NEXT

20. (x,y) property of x-y conclusion
(1,1) 1-1 even (1,1) R
(1,2) 1-2 odd (1,2) R
(1,3) 1-3 even (1,3) R
(2,1) 2-1 odd (2,1) R
(2,2) 2-2 oven (2,2) R
(2,3) 2-3 odd (2,3) R
Hence R={ (1,1), (1,3), (2,2)}.
(b)
Yes. 1R1 since (1,1) R.
No. 2R3 since (2,3) R.
Yes. 1R3 since (1,3) R.
NEXT

21. Let A={1,2,3} and a binary relation E be defined by
(x,y) E iffx-y is even and x,y A. Then E={ (1,1),
(2,2), (3,3), (1,3), (3,1)} can be represented by the
following digraph
(2,2):
2-2=0 even, hence the loop at vertex labelled by 2
A.
(1,3):
1-3=-2 even, hence the arrow from vertex 1 to
vertex 3. >>>>>