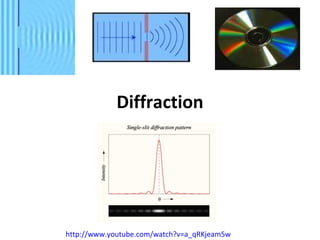
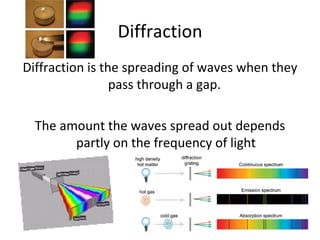
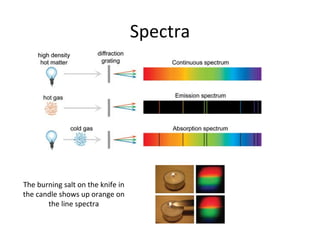
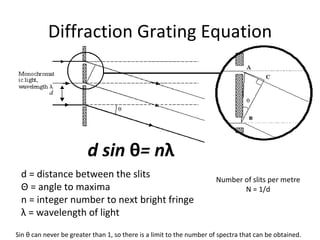
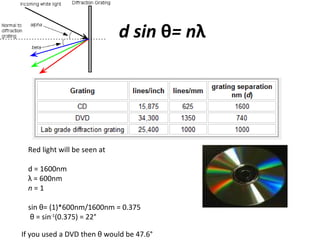
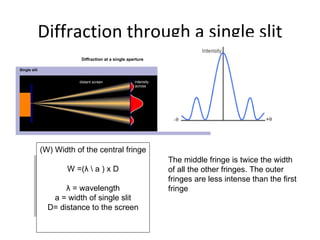
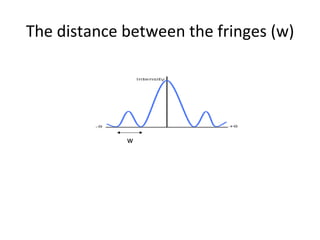
The document discusses the principles of diffraction gratings and how they can be used to calculate various properties of light. Specifically, it explains the diffraction grating equation, provides examples of how to use it to determine the wavelength of light and angle of diffraction for different grating spacings and orders. It also describes how a grating's line spacing can be used to calculate the slit spacing and discusses the angular spread of a spectrum produced from a grating.

1. Diffraction http:// www.youtube.com/watch?v =a_qRKjeam5w

2. Diffraction Diffraction is the spreading of waves when they pass through a gap. The amount the waves spread out depends partly on the frequency of light

3. Spectra The burning salt on the knife in the candle shows up orange on the line spectra

4. Diffraction Grating Equation d sin θ = n λ d = distance between the slits Θ = angle to maxima n = integer number to next bright fringe λ = wavelength of light Number of slits per metre N = 1/d Sin θ can never be greater than 1, so there is a limit to the number of spectra that can be obtained.

5. d sin θ = n λ Red light will be seen at d = 1600nm λ = 600nm n = 1 sin θ = (1)*600nm/1600nm = 0.375 θ = sin -1 (0.375) = 22° If you used a DVD then θ would be 47.6°

6. Grating question A grating is labelled '500 lines per mm'. 1. Calculate the spacing of the slits in the grating. 2. Monochromatic light is aimed straight at the grating and is found to give a first-order maximum at 15 0 . Calculate the wavelength of the light source. 3. Calculate the position of the first-order maximum when red light of wavelength 730 nm is shone directly at the grating. 4. The longest visible wavelength is that of red light with λ = 750 nm. The shortest visible wavelength is violet where λ = 400nm. Use this information to calculate the width of the angle into which the first-order spectrum is spread out when white light is shone onto the grating. A grating is illuminated with a parallel beam of light of wavelength 550 nm. The first-order maximum is in a direction making an angle of 20 0 with the straight-through direction. 5. Calculate the spacing of the grating slits. 6. What would be the angle of the first-order maximum if a grating of slit spacing of 2.5 x 10 –6 m were used with the same light source? 7. Calculate the wavelength of light that would give a second-order maximum at q = 32 0 with a grating of slit spacing 2.5 x 10 –6 m d sin θ = n λ

7. Grating answers d sin θ = n λ 3.

8. Grating answers 4.

9. Diffraction through a single slit The middle fringe is twice the width of all the other fringes. The outer fringes are less intense than the first fringe (W) Width of the central fringe W =( λ \ a ) x D λ = wavelength a = width of single slit D= distance to the screen

10. The distance between the fringes (w) w