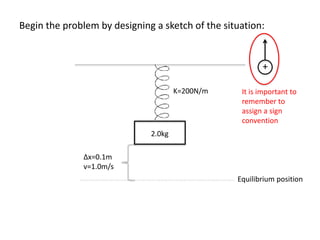
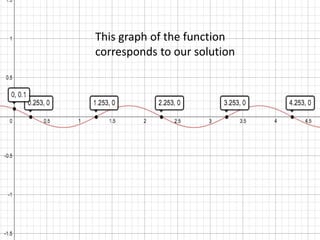
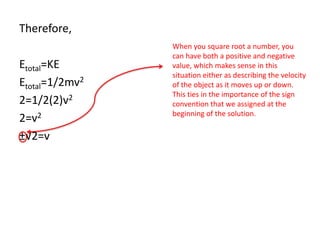
This document describes a 2kg mass oscillating on a vertical spring with a spring constant of 200N/m and completing one oscillation every 2 seconds. An equation of motion is derived using the given information and simple harmonic motion equations. The equation is x(t)=0.14cos(πt+0.775), which models the position of the mass as a function of time t. The intervals when the displacement is negative are (0.253+2n, 1.253+2n) where n is an integer. The maximum velocity achieved by the mass is determined to be ±√2 m/s through an energy analysis.

1. Physics Learning Object
SIMPLE HARMONIC MOTION OF
A MASS ON A VERTICAL SPRING

2. Consider a 2.0kg mass hanging from a vertical
spring with a spring constant, k, of 200N/m. The
mass is oscillating, completing 1 oscillation every
2.0 seconds. At a given time, the mass is travelling
at 1.0m/s when it is 0.1m away from the
equilibrium position. If we consider the distance of
0.1m as the starting point of the oscillation (at t=0),
a) Write an equation to model the position of the
simple harmonic motion described using the
cosine function.
b) Determine the intervals during which the
displacement is negative.
c) Determine the maximum velocity that the mass
achieves.

3. Begin the problem by designing a sketch of the situation:
Equilibrium position
K=200N/m
Δx=0.1m
v=1.0m/s
2.0kg
+
It is important to
remember to
assign a sign
convention

4. a) Write an equation using the cosine function to
model the position of the simple harmonic motion
described.
Consider the equation of simple harmonic motion:
x(t)=Acos(ωt+Φ)
In order to write the equation for this particular
situation, we must determine constants A, ω, and Φ

5. To find the constant A, we must first find the total
energy of the system. Since the mass is already in
motion, we can think about the total energy as the sum
of the potential energy and of the kinetic energy:
Etotal=PE+KE
Substituting the work equation for a spring into the
potential energy, we get:
Etotal=1/2kΔx2+1/2mv2

6. Now plug in the given values and solve for Etotal:
k=200N/m m=2.0kg
Δx=0.1m v=1.0m/s
Etotal=1/2kΔx2+1/2mv2
Etotal=1/2(200)(0.1)2+1/2(2.0)(1.0)2
Etotal=1+1
Etotal= 2 J

7. Now that we have the total energy, we can solve for the
maximum amplitude. At the maximum amplitude, all of the
energy in the system is transformed into potential energy:
Etotal=PE+KE
Etotal=1/2kΔx2
We can now solve for Δx
Etotal=1/2kΔx2
2=1/2(200)Δx2
0.02=Δx2
0.14m=Δx
Since the amplitude is equal to Δx,
A=0.14
0

8. Now we need to find the angular frequency, ω. We
know the time it takes for one period is 2.0s, so we can
easily solve for ω:
ω=2π/T
ω=2π/2
ω=π

9. Plugging in A and ω into the equation for simple harmonic
motion we get:
x(t)=0.14cos(πt+Φ)
We also know that at t=0, the mass is 0.1m away from the
equilibrium point:
x(0)=0.14cos(π(0)+Φ)
Simplify:
0.1=0.14cos(Φ)
0.714=cos(Φ)
cos-1(0.714)=Φ
0.775=Φ

10. So the equation of the function that describes the
position of the mass as a function of time is:
x(t)=0.14cos(πt+0.775)

11. b) Determine the intervals during which the displacement is
negative.
To answer this question we need to first find the zeros of the
function and then use the symmetry of the cosine function to
find where these zeros repeat.
We begin by setting the cosine function to zero:
0=0.14cos(πt+0.775)
Simplify:
0=cos(πt+0.775)
cos-1(0)=πt+0.775
1.57-0.775=πt
0.253=t

12. The first zero of this function is at t=0.253 and we know
from the question that it will repeat this oscillation
every 2 seconds, crossing the x-axis once in between
this oscillation. So the zeros of the function can be
described as:
0=x(0.253)
0=x(0.253+1)
0=x(0.253+2)
0=x(0.253+2)
Etc..
0=x(0.253+n), where n is an integer

13. Now we plug in a point between any of these zeros to
determine whether the value is positive or negative:
X(0.5)=0.14cos(π(0.5)+0.775)
X(0.5)= -0.098
Since the value is negative we know that the interval
(0.253,1.253) is negative, and repeats every 2s. So the
displacement is negative for
(0.253+2n,1.253+2n), where n is an integer

14. This graph of the function
corresponds to our solution

15. c) Determine the maximum velocity that the mass
achieves.
Again we can think about this problem in terms of
energy. At maximum velocity, all of the potential energy
of the system has been transformed into kinetic energy.
(Note that this occurs when the object passes through
the equilibrium point).

16. Therefore,
Etotal=KE
Etotal=1/2mv2
2=1/2(2)v2
2=v2
±√2=v

17. Therefore,
Etotal=KE
Etotal=1/2mv2
2=1/2(2)v2
2=v2
±√2=v
When you square root a number, you
can have both a positive and negative
value, which makes sense in this
situation either as describing the velocity
of the object as it moves up or down.
This ties in the importance of the sign
convention that we assigned at the
beginning of the solution.