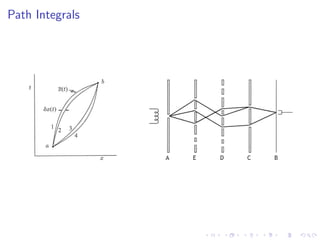
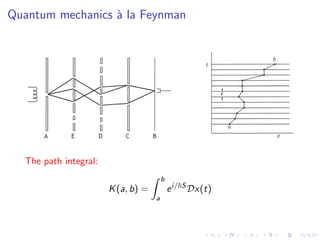
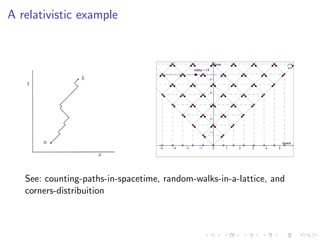
This document discusses the path integral formulation of quantum mechanics and its application to relativistic theories like general relativity. It introduces causal dynamical triangulations as an approach to quantizing gravity by defining a path integral over causal triangulations of spacetime geometries. This allows imposing global hyperbolicity and causality constraints to avoid issues like wormholes and baby universes. The approach aims to make quantum gravity computations possible using desktop computers by dynamically triangulating Lorentzian spacetimes.

1. Causal Dynamical Triangulations
Israel Garc´ıa
@renegarxia
20 de mayo de 2015

2. Table of contents
The classical action
Quantum mechanics
Path Integrals in relativity

3. Path Integrals

4. Some waves

5. More waves (click to watch them)

6. Path Integrals
With xa, xb fixed, how do we minimize S?
S =
tb
ta
L(˙x, x, t)dt (action)
L =
m
2
˙x2
− V (x, t) (Lagrangian)

7. Path Integrals
Set x → x + δx, then
L →
m
2
(˙x + δ ˙x)2
− V (x + δx, t),
=
m
2
˙x2
+ m ˙xδ ˙x +
m
2
δ ˙x2
− V (x, t) − ∂x V (x, t)δx − O(δx2
),
Therefore,
L → L + m ˙xδ ˙x +
m
2
δ ˙x2
− ∂x V (x, t)δx − O(δx2
),
What happens to the action? (S)

8. The Action
S →
tb
ta
L + m ˙xδ ˙x +
m
2
δ ˙x2
− ∂x V (x, t)δx − O(δx2
) dt,
= S +
tb
ta
m ˙xδ ˙x − ∂x V (x, t)δx dt (up to first order)
With fixed extremes, δxa = δxb = 0. Integration by parts follows:
S → S −
tb
ta
(m¨x + ∂x V (x, t)) δx dt

9. Least action
The true x is such that, if
x → x + δx,
then S is the same, to first order. The true trajectory obeys this
equation:
m¨x = −∂x V (x, t),
which is the second law of mechanics in disguise.

10. Quantum mechanics `a la Feynman
The path integral:
K(a, b) =
b
a
ei/ S
Dx(t)

11. A relativistic example
See: counting-paths-in-spacetime, random-walks-in-a-lattice, and
corners-distribuition

12. Path integrals in relativity
There’s an action principle for general relativity:
SEH =
1
G
d4
x det g (R − 2Λ) (Einstein-Hilbert action)
Problem: Make sense of the path integral:
g∈G
Dg eiSEH

13. So, you want to quantize gravity?
String theory.
Loop quantum gravity.
Euclidean quantum gravity.
Causal dynamical triangulations.

14. What is curvature?

15. Discrete curvature

16. Euclidean Gravity
This is Wick’s rotation:
−dt2
+ dx2
→ d(i t)2
+ dx2
It makes gravity euclidean.
And turns amplitudes into probabilities!

17. First attempt: failed!

18. Causality (you can’t kill your parents...)
...before you are born...

19. Global hyperbolicity
This is acceptable: This is not:
Wormhole, baby universes.

20. Causal triangulations

21. Quantum gravity in your desktop

22. References I
J. Ambjorn, A. Goerlich, J. Jurkiewicz, and R. Loll, Quantum
Gravity via Causal Dynamical Triangulations.
Jan Ambjorn, J. Jurkiewicz, and R. Loll, Dynamically
triangulating Lorentzian quantum gravity, Nucl.Phys. B610
(2001), 347–382.
J. Ambjorn, J. Jurkiewicz, and R. Loll, The Universe from
scratch, Contemp.Phys. 47 (2006), 103–117.
R. Loll, The Emergence of spacetime or quantum gravity on
your desktop, Class.Quant.Grav. 25 (2008), 114006.