1. 分枝カット法に基づいた線形符号の復号法に関する一考察 堀井 俊佑 松嶋 敏泰 平澤 茂一 早稲田大学

2. 研究背景 対象とする問題 無記憶通信路に対する 2 元線形符号の最尤復号 LDPC 符号・ターボ符号に対しては，確率伝搬法が幅広く用いられている 近年，線形計画法に基づいた復号法に関する研究が盛ん（ LP 復号法 ） LP 復号法の性能 整数解が得られれば最尤であることが保証される 計算量は一般的に，確率伝搬法より多い 復号誤り率も，確率伝搬法より劣ることが多い ⇒ 復号アルゴリズムを改良する研究が多く存在

3. 関連研究と本研究の目的 分枝限定法に基づく復号 [Yang et al.] 分枝限定法を利用 逐次的に等式制約を問題に組み込む 最尤復号が保証される Adaptive LP (ALP) 復号 [Taghavi et al.] LP の計算量削減 逐次的に不等式を問題に組み込む 不等式の候補を増やすことで， 復号誤り率が改善 組合せ 分枝限定法と ALP の組合せ． 逐次，等式制約・不等式制約を問題に組み込む． 最尤復号が保証される． 分枝カット法に基づく復号という形で一般化 本研究 [Draper et al.] によって提案されている復号法も分枝カット法の 1 つと見ることができる

4. 線形符号の最尤復号問題 （通信路は無記憶を仮定． AWGN 等） 最尤復号問題 最適化問題の形に変換 (1) (2)

5. 従来研究： LP 復号法 LP 復号法 得られた解が整数解ならば，その解は最尤解である． (6)

6. 従来研究： Adaptive LP 復号法 必要な不等式を逐次問題に組み込んでいく Adaptive LP ( 切除平面法 ) 不等式が見つかる 新たな不等式が無い． 最後に解いた最適化問題の最適解を出力 ※ 途中で見つかった不等式を カット（切除平面） と呼ぶ． 探索する不等式の範囲が (6) 式であれば，出力は LP 復号法と同じ．

7. 従来研究： Adaptive LP 復号法 不等式の探索範囲を広げることで， 新たなカットが見つかれば，復号誤り率が改善される場合がある． ただし，計算量も増大する． 符号の場合，パリティ検査式の排他的論理和をとることで，冗長なパリティ検査式 (RPC) を構成できる． [Taghavi et al.] による RPC の探索アルゴリズム Step1: ALP の結果得られた解を とする Step2: タナーグラフから，整数解のノードを取り除く Step3: 得られたグラフ上でランダムウォークもしくは探索によりサイクルを見つける Step4: サイクルに含まれるパリティ検査式の排他的論理和をとる Step5: パリティ検査式がカットを生成すれば終了．そうでなければ Step3 に戻る． 上記を決められた回数だけ行う．回数が多ければカットが見つかる確率が大きくなるが，計算量が多くなる．

8. 従来研究：分枝限定法に基づく復号 LP decoder の出力が，非整数ならば，等式制約を加えて解きなおす． 復号の過程は，木で表現できる． 各ノードは， LP とその解，目的関数値を保持．根ノードには (6) の LP ．その他のノードは，親ノードの LP に等式制約を 1 つ加えた LP が対応する． 分枝限定法 Step.1 ： Step.2 ： Step.3 ： Step.4 ：

9. 従来研究：分枝限定法に基づく復号 復号過程の例 : 最尤符号語

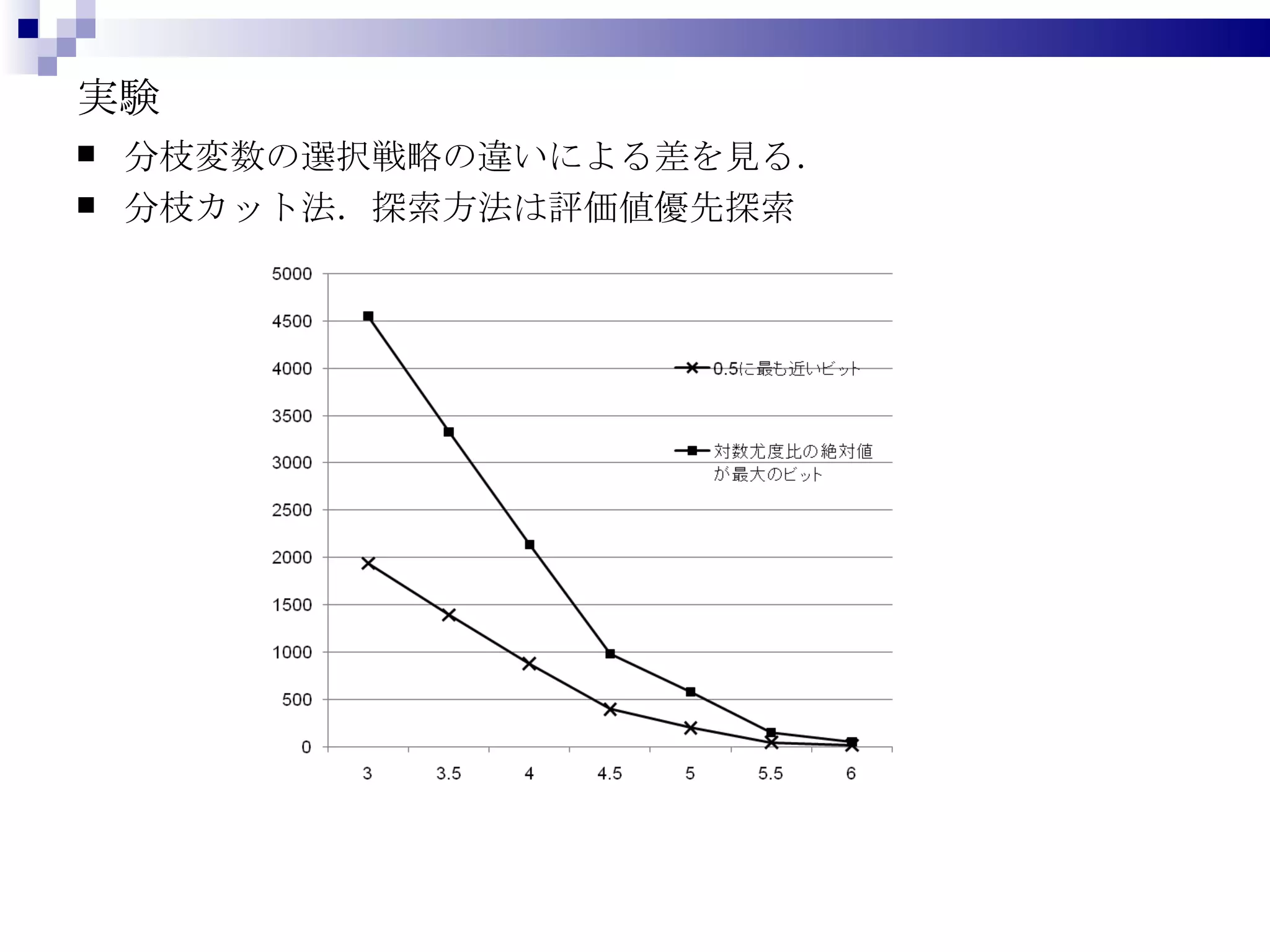
10. 分枝限定法の計算戦略 探索の仕方には，幾つかの選択肢がある 深さ優先探索 幅優先探索 評価値優先探索 ヒューリスティック探索 etc 子問題を生成する際に，どのビットに整数制約を入れるか（分枝変数の選択）によってもアルゴリズムの性能は大きく変化する． 親ノードの LP の最適解において，値が 0.5 に最も近いビット 対数尤度比が最も大きいビット ループが多く解消されるビット etc. ※ [Yang et al.] では，深さ優先・幅優先のみ ※ [Yang et al.] では， (6) の LP の最適解が， 0.5 に近い順．これだと，子ノードの LP が親ノードの LP と変わらない場合が生じる．

11. 分枝カット法に基づいた復号 Step.1 ： Step.2 ： Step.3 ： Step.4 ： 分枝限定法にカットの探索を組み込む

12. 分枝カット法の計算戦略 分枝限定法と同様，探索の仕方・子問題の選択に自由度がある． その他に，「カットの候補となる不等式の集合」の取り方に関する自由度がある． 不等式の集合を多く取っておけば， 1 つ 1 つの LP を解く時間が大きくなるが，探索ノード数の減少が見込める． 符号語であることを保証するためには，全ての不等式を満たす整数ベクトルが符号語であることが条件 以下のようにすると， [Draper et al.] のアルゴリズムが復元される 探索方法は，幅優先探索 子問題の生成は， 「親ノードの最適解が 0.5 に近いビット」に等式制約を入れる． 不等式の探索範囲は (6) 式

13. 実験 探索の仕方の違いによる，探索ノード数の差を見る 分枝限定法・子問題の生成法は [Draper et al.] のもの (60,30)- 正則 LDPC 符号を使用 評価値優先探索が一番少ない．

14. 実験 評価値優先探索では，リストのソート作業が入るので，ノード数の比較だけでは公平でない．計算時間で比較． グラフの形が，探索ノード数と殆ど変わらない．ソートにかかる時間に比べて， LP を解く時間の方が支配的．

15. 実験 分枝変数の選択戦略の違いによる差を見る． 分枝カット法．探索方法は評価値優先探索

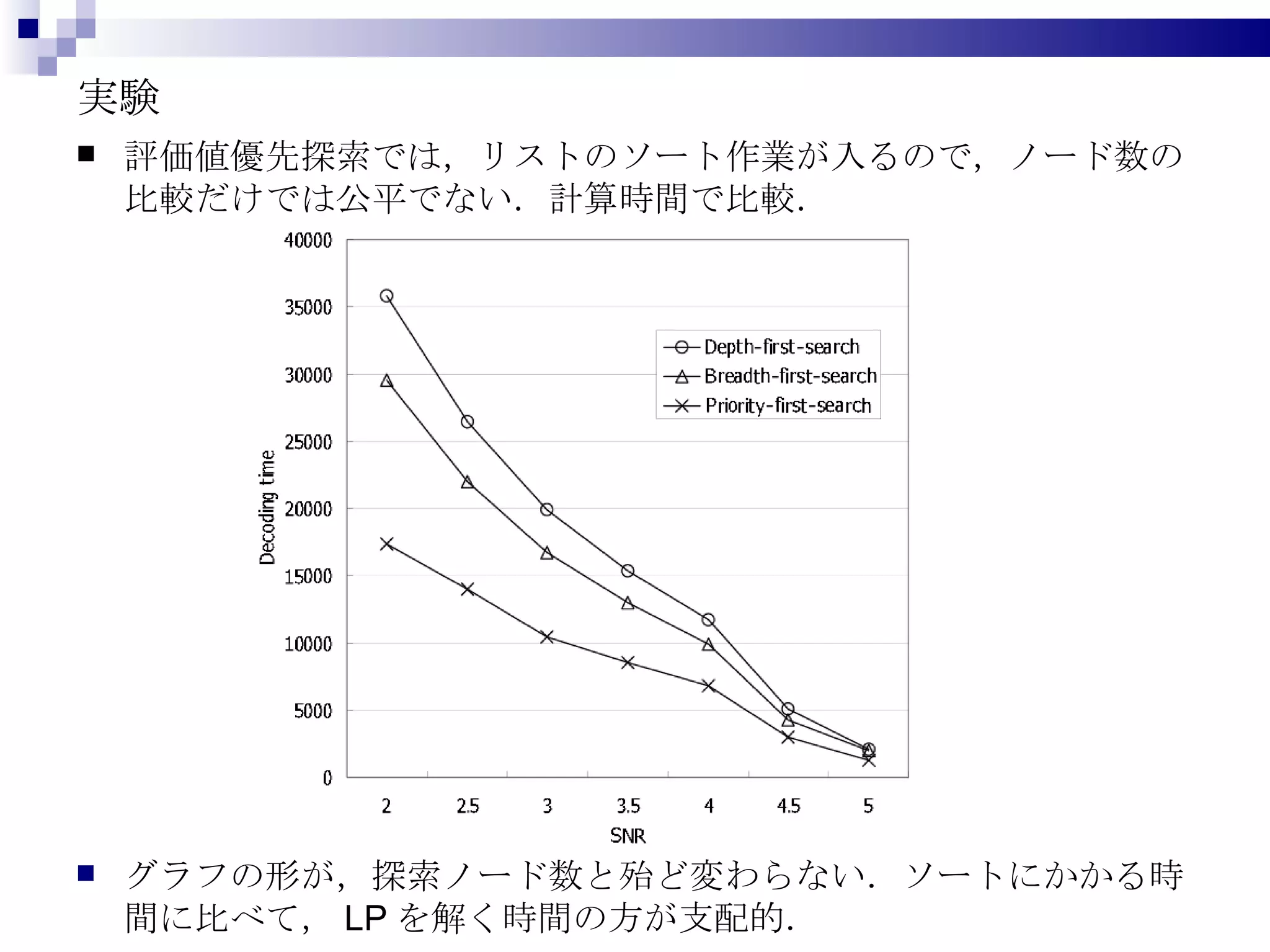
16. 実験 分枝限定法と分枝カット法の違い 探索方法は評価値優先探索．子問題の生成法は [Draper et al.] のもの．カットの候補となる不等式集合は元の LP （分枝限定法と同じ探索） 分枝カット法のほうが早い（ LP と ALP の差が出ているのみ．）

17. 実験 分枝カット法におけるカット探索範囲の違い 探索方法は評価値優先探索．子問題の生成法は [Draper et al.] のもの． [Taghavi et al.] の RPC 探索アルゴリズムを使用．（最大繰り返し回数 10 回）

18. まとめと今後の課題 分枝カット法に基づいた復号法というアルゴリズムの枠組みを提案した． いくつかの従来の復号法がこの枠組みに含まれることを示した． ノードの選択・分枝変数の選択・不等式の探索範囲などを変更することで，より良いアルゴリズムが得られることを示した． 符号の構造を活用したより良い計算戦略の提案が今後の課題である．

19. 付録 (6) 式の制約を満たさない⇒符号語にならない 符号語が (6) 式を満たさないとする ⇒ N ( j ) において， S に含まれるビットは 1 ，それ以外のビットは 0 ⇒ 対応するベクトルは j 行目のパリティ検査式を満たさず，符号語にならない． 符号語でない整数ベクトル⇒ (6) 式を満たさない 符号語で無ければ，パリティ検査式を満たさない行 j が存在する． ⇒ 以下を満たす V が存在する．