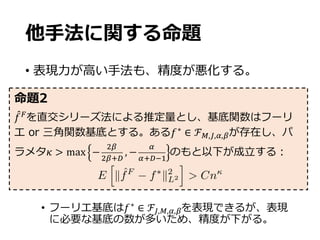
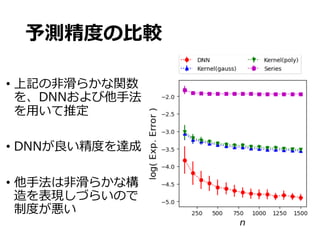
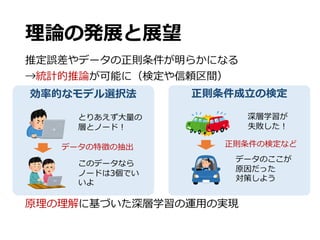
The document appears to discuss mathematical functions, particularly focusing on piecewise smooth functions and their characterizations. It introduces various mathematical concepts including norms, smooth function sets, and optimization criteria. Additionally, there are references to specific formulations and calculations related to these functions.

1. ()0 () +) q
r s

2. ”
A& YNVfaYV &:aWaYVfa
h8RR BRa NX BR c W RN Z B Z FY U :aZP V Z
9SSRP VbRXei U 2 N dVb& T NO )0( &(,,/,
y k

3. m

4. • r q n8BBs
8BB o
w
q
uhi t
)m5X UN
m

5. ” zyz y y
v l k
”
” p
y
y
x p
q

6. x
•
• 7U YNZ WN ()- 5 FG5GF
• ~ NcNTaPUV ()/ B DF
•
• LN We ()/ BB
• q FNS NZ ()/ 7A
• F
• MUNZT ()/ 7 E
• FafaWV ()0 5 FG5GF
8BB ”

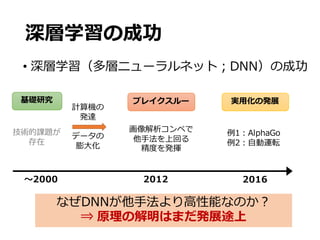
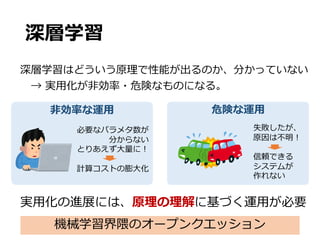
7. S
• !" ∈ ℱ%%
!∗
: [0,1]-
→ ℝ
Y = !∗
2 + 4
5 i.i.d. 26, 76 689
:
ℱ%% DNN
7
d
k ˆf f⇤
k2

8. 00snt
<2 r s =ℓ2
?: ℝ@ℓ → ℝ@ℓ2 r s ℓ = 1, … ,<
!ℓ B ≔ ? DℓB + Eℓ ℓ = 1, … , <
rDℓ: =ℓ×=ℓG9 Eℓ2 =ℓ s
snt
ℱ%% ≔ ! B = !H ∘ !HG9 ∘ ⋯∘ !9 B

9. 00
?”ER H
? B = (max B9,0 ,… ,max B-,0 )
8BB r < = 6s
!ℓ B ≔ ? DℓB + Eℓ
B
? B
0

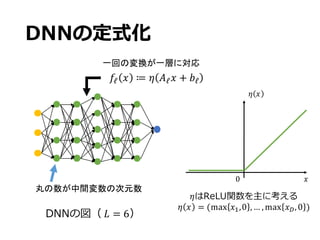
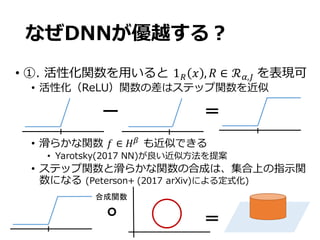
10. S
• x
• 8BB !" ∈ ℱ%% ”
~y o
!∗
: [0,1]-
→ ℝ
Y = !∗
2 + 4
5 i.i.d. 26, 76 689
:
ℱ%% DNN
d
k ˆf f⇤
k2

11. dg m
• y
!∗
c x 8BB
r q q BB Z RR s
k
q !"(B) = ∑ RST(B,2S)S
T B, B′ 2 q
q !"(B) = ∑ RSVS BS
VS B 2 rR&T& q s

12. dg m
• y
!∗
”8BB” y
2 6 ( ,2
!∗
: 0,1 -
→ ℝ x
!" ”
k ”YVZVYNd q x k
E
h
k ˆf f⇤
k2
2
i
= O
⇣
n 2 /(2 +D)
⌘

13. q

14. c
•
”
y
Pd c WX
~
r ” s
Y∗
!∗
c 8BB o

15. • 8BB l
• FafaWV G& ()0 & :N XRN ZVZT N R S RR XRN ZVZT bVN N
WR ZRX R RP VbR& A E J 7D 5 FG5GF
• FPUYV VROR & ()/ & B Z N NYR VP RT R V Z a VZT
RR ZRa NX ZR c W cV U ER H NP VbN V Z SaZP V Z& &
• BRe UNOa 6& G YV WN E& F RO B& ()- & B Y
ON R PN NPV e P Z X VZ ZRa NX ZR c W &
• FaZ F& 7URZ J& JNZT & Va G& L& ()- & N TR
YN TVZ RR ZRa NX ZR c W 2 UR e NZ NXT V UY
• ” ” y

16. d c
r 0,1 Z + ~ y s
w c
196 6A9 6 2 8 9
”
” B9
BZ
! B9,BZ

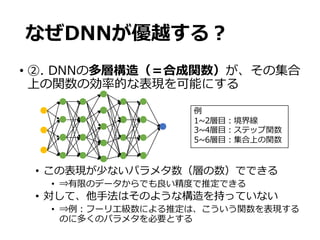
17. w c
•
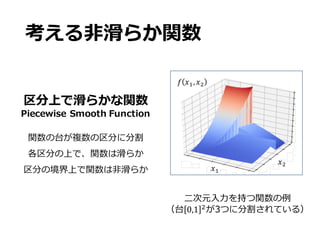
• 1. [0,1]-
• 2. [0,1]-
• )& [0,1]-
• m q
• m q
G[✓`](x) = x(`)
,
where x` is defined inductively as
x(0)
:= x,
x(`0)
:= ⌘(A`0 x(`0 1)
+ b`0 ), for `0
= 1, ..., ` 1,
where ⌘ is an element-wise ReLU function, i.e., ⌘(x) = (max{0, x1}, ..., max{0, x
Here, we define that c(✓) denotes a number of non-zero parameters in ✓.
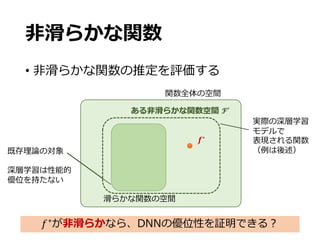
1.2. Characterization for True functions. We consider a piecewise smooth
functions for characterizing f⇤. To this end, we introduce a formation of
some set of functions.
Smooth Functions Secondly, a set for smooth functions is introduced.
With ↵ > 0, let us define the H¨older norm
kfkH := max
|a|b c
sup
x2[ 1,1]D
|@a
f(x)| + max
|a|=b c
sup
x,x02[ 1,1]D
|@af(x) @af(x0)|
|x x0| b c
,
and also H ([ 1, 1]d) be the H¨older space such that
H = H ([ 1, 1]D
) := f : [ 1, 1]D
! R |kfkH  CH ,
where CH is some finite constant.
Date: January 13, 2018.
H = H ([0, 1]D
) = f : [0, 1]D
! R|kfkH < 1

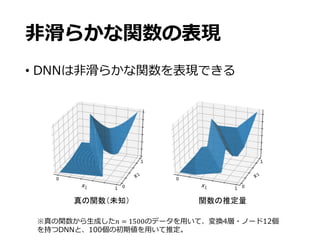
18. ℝ-
[0,1]-
]
^ k R k
w c
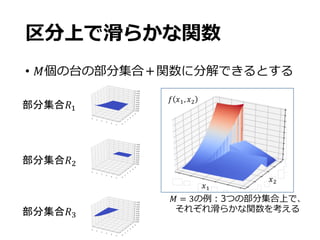
• 2. [0,1]-
• m
• _-G92 ` _̅-G92 `
• b9,… ,bcmℝ- dS2_̅-G9 → bS 2
ℬc,f ≔ E: _-G9
→ ℝ-
g5hijkgli,E@ ∘ dS ∈ mf
, = ∈ ` , h ∈ ^
E_-G9

19. w c
• 2. [0,1]-
• n(⋅)
•
ℛc,f ≔ n E ∩ 0,1 -
: E ∈ ℬc,f
3 3 6
8a XRe )1/, 5G
n E
” y R
R = 2 [0,1]-

20. w c
•
• 0,1 -
• r
• 1s(B)” t rB ∈ t 1 s
• tu ”R
• !u”v
ℱc,w,f,x = y !u B 1sz
B
u∈ w
: !u ∈ mx
, tu ∈ ℛc,f

21. w c
• r t
B9
BZ
! B9,BZ
t9
r = 3 m+
“
tZ
t|

22. •
• ~
•
!"H
≔ argmin
Å∈ℱÇÇ
∑ 76 − ! 26
Z:
689
N
D

23. •
• y
• ” y
ΠÖ ! S ! ∈ ℱ%%
ΠÖ ”BB r s
dΠÖ !|` ∝ exp −∑ 76 − ! 26
Z
6∈ : ãGZ
dΠÖ !
` = 26, 76 6∈[:]2 q ãZ
2
!"å ≔ ∫ !=ΠÖ(!|`)
rh y
N
D

25. • ” q
!∗
∈ ℱw,c,f,x k éè 1 +
x
-
+
f
Z-GZ
Θ 5
ë
íìîë + 5
ëïñ
óîëïñ 8BB z
m
x m ! ∈ mx
q
m E ∈ ℬc,f q
éè
k ˆfL
f⇤
k2
L2 = ˜O
⇣
max
n
n 2 /(2 +D)
, n ↵/(↵+D 1)
o⌘

26. • q
!∗
∈ ℱw,c,f,x k éè 1 +
x
-
+
f
Z-GZ
Θ 5
ë
íìîë + 5
ëïñ
óîëïñ 8BB z
m
8BB ” q
E
h
k ˆfB
f⇤
k2
L2
i
= ˜O
⇣
max
n
n 2 /(2 +D)
, n ↵/(↵+D 1)
o⌘

27. 00
• q ”
q x
• u o 9 9 3B yy
y k
!̅ k x ò > 0
m
inf
¯f
sup
f⇤2FM,J,↵,
E
⇥
k ¯f f⇤
k2
L2
⇤
> C max
n
n 2 /(2 +D)
, n ↵/(↵+D 1)
o

28. d
• y ” y
• !∗
∈ ℱc,w,f,x z ” q
E F ” y
!"ö
q k q ”
Na VNZ q k
x !∗
∈ ℱc,w,f,x òö > 0 m
E
h
k ˆfK
f⇤
k2
L2
i
! CK > 0.

29. d
• y k
• q ”!∗
∈ ℱc,w,f,x
y k
!"õ
q ” q
kx !∗
∈ ℱw,c,f,x
ú > max −
Zx
Zxù-
, −
f
fù-G9
m
E
h
k ˆfF
f⇤
k2
L2
i
> Cn

30. ec c d
• r s
• 8BB
• ” y 8BB
k
• 8BB ”
• ” ~
x
-
+
f
Z-GZ
x
• ” q Θ 5
ë
íìîë + 5
ëïñ
óîëïñ

31. 8BB” y o

32. 00S d
• & y 1s B , t ∈ ℛf,c
• rER Hs ”
• ! ∈ mx
• LN We ()/ BB y
• ”
DR R Z ()/ N KVb
∘

33. 00S d
• & 8BB
• y r s
• w q y
• ” z y y
• w m q ” zyz
)g m
+g, m
-g. m

35. c
• 8BB”
u 5 = 1500 q y , l q )
8BB )(( y k

36. •
8BB
y
• 8BB y
• ”
y
y

38. a
•
• 8BB y
•
• 8BB
• 8BB r
s
8BB o
x n d S c c

39. ×
q
v r s
y
snt
x
q p
q
q ”+ y
y
q
p
q
z

40. x z y k

41. • F ZR 7& & )10 & C VYNX TX ONX N R S P ZbR TRZPR S Z Z N NYR VP RT R V Z&
GUR NZZNX S N V VP )(,( )(-+&
• FafaWV G& ()0 & :N XRN ZVZT N R S RR XRN ZVZT bVN N WR ZRX R RP VbR& A E
J 7D 5 FG5GF &
• FPUYV VROR & ()/ & B Z N NYR VP RT R V Z a VZT RR ZRa NX ZR c W cV U
ER H NP VbN V Z SaZP V Z& N KVb&
• BRe UNOa 6& G YV WN E& F RO B& ()- & B Y ON R PN NPV e P Z X VZ ZRa NX
ZR c W & A E J 7D 7C G &
• FaZ F& 7URZ J& JNZT & Va G& L& ()- & N TR YN TVZ RR ZRa NX ZR c W 2
UR e NZ NXT V UY N KVb&
• 7U YNZ WN 5& RZNSS A& AN UVRa A& 5 a & 6& R7aZ L& ()/ GUR X
a SNPR S YaX VXNeR ZR c W & A E J 7D 5 FG5GF &
• NcNTaPUV & (). & 8RR XRN ZVZT cV U a X PNX YVZVYN& Z 5 bNZPR VZ BRa NX
ZS YN V Z D PR VZT Fe RY &
• LN We 8& ()/ & 9 O aZ S N dVYN V Z cV U RR ER H ZR c W & BRa NX
BR c W 1, )(+ )),&
• FNS NZ & FUNYV C& ()/ & 8R U cV U N R SS VZ N dVYN VZT ZN a NX SaZP V Z
cV U ZRa NX ZR c W & A E J 7D 7A &
• MUNZT 7& 6RZTV F& N A& ERPU 6& IVZeNX C& (). & HZ R NZ VZT RR
XRN ZVZT R aV R R UVZWVZT TRZR NXVfN V Z& 7 E&
• Ka 5& ENTVZ We A& ()/ & ZS YN V Z UR R VP NZNXe V S TRZR NXVfN V Z PN NOVXV e
S XRN ZVZT NXT V UY & Z 5 bNZPR VZ BRa NX ZS YN V Z D PR VZT Fe RY &

42. • y
• U 2 ccc&V N a eN&P Y