The document discusses the application of formal language concepts, specifically context-free grammar and hyperedge replacement grammar (HRG), to the problem of molecular graph generation. It introduces a molecular hypergraph grammar (MHG) that aims to satisfy certain constraints, particularly valence conditions essential for valid molecular structures. The document also outlines a corresponding HRG inference algorithm that helps reconstruct input hypergraphs and ensures the proper generation of molecular graphs through a probabilistic model.














![© 2019 IBM Corporation
/52
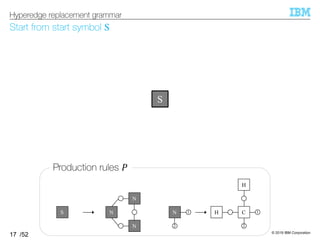
Hypergraph is a generalization of a graph
§Hypergraph W = (T, X) consists of…
–Node Y ∈ T
–Hyperedge Z ∈ X ⊆ 2 ]
: Connect an arbitrary number of nodes
cf, An edge in a graph connects exactly two nodes
15
Hyperedge replacement grammar
HyperedgeNode](https://image.slidesharecdn.com/20191120ibis-191120000917/85/Graph-generation-using-a-graph-grammar-15-320.jpg)
![© 2019 IBM Corporation
/52
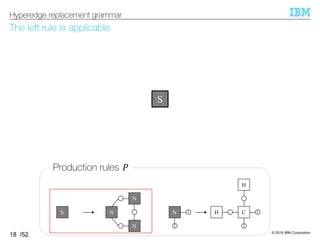
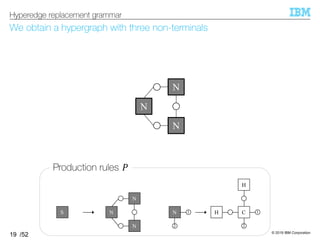
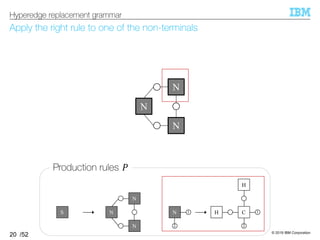
HRG generates a hypergraph by repeatedly replacing
non-terminal hyperedges with hypergraphs
§Hyperedge replacement grammar (HRG) 5 = (T, Σ, U, =)
–T: set of non-terminals
–Σ: set of terminals
–=: start symbol
–U: set of production rules
– A rule replaces a non-terminal hyperedge with a hypergraph
16
Hyperedge replacement grammar
1C
2
H
H1N
2
N
N
NS
Labels on hyperedges
C
N
S
[Feder, 71], [Pavlidis+, 72]](https://image.slidesharecdn.com/20191120ibis-191120000917/85/Graph-generation-using-a-graph-grammar-16-320.jpg)
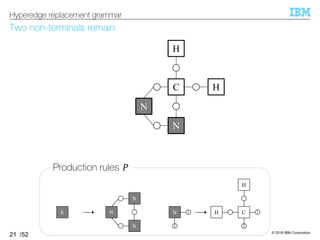
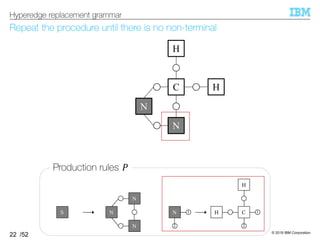
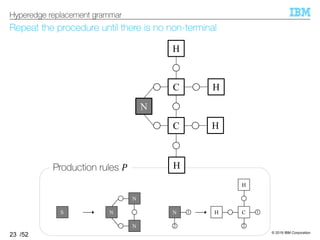
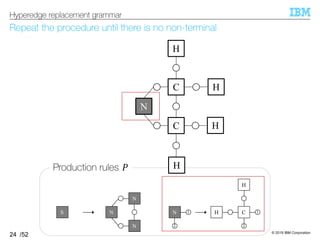
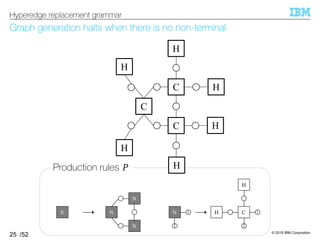

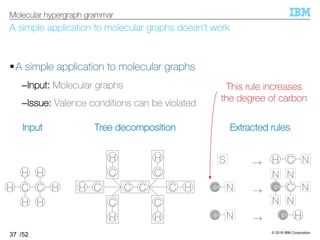
![© 2019 IBM Corporation
/52
HRG inference algorithm outputs HRG that can reconstruct the input
§HRG inference algorithm [Aguiñaga+, 16]
–Input: Set of hypergraphs ℋ
–Output: HRG such that ℋ ⊆ ℒ(HRG)
Minimum requirement of the grammar’s expressiveness
–Idea: Infer production rules necessary to obtain each hypergraph
Decompose each hypergraph into a set of production rules
27
HRG inference algorithm
Language of the grammar](https://image.slidesharecdn.com/20191120ibis-191120000917/85/Graph-generation-using-a-graph-grammar-27-320.jpg)
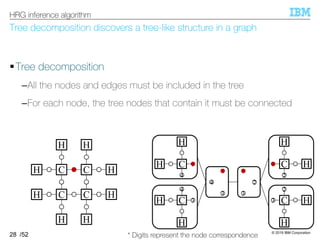
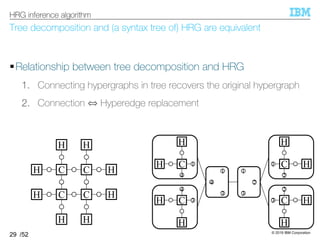
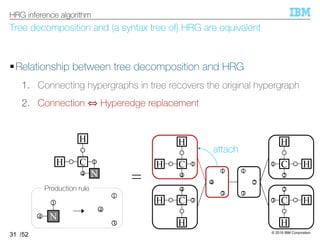
![© 2019 IBM Corporation
/52
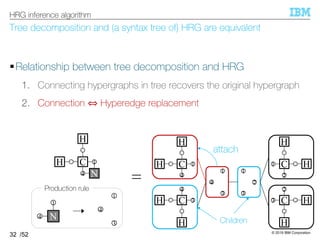
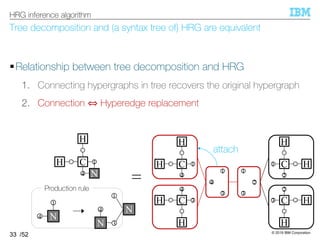
HRG can be inferred from tree decompositions of input hypergraphs.
§HRG inference algorithm [Aguiñaga+, 16]
–Algorithm:
–Expressiveness: ℋ ⊆ ℒ(HRG)
The resultant HRG can generate all input hypergraphs.
(∵ clear from its algorithm)
34
HRG inference algorithm
1. Compute tree decompositions of input hypergraphs
2. Extract production rules
3. Compose HRG by taking their union](https://image.slidesharecdn.com/20191120ibis-191120000917/85/Graph-generation-using-a-graph-grammar-33-320.jpg)



![© 2019 IBM Corporation
/52
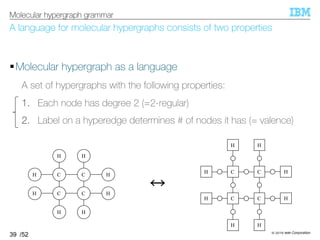
MHG, a grammar for the language, is defined as a subclass of HRG
§Molecular Hypergraph Grammar (MHG)
–Definition: HRG that generates molecular hypergraphs only
–Counterexamples:
40
Molecular hypergraph grammar
MHG
HRG
C C
H
H
HH
H
HH
C C
H
H
HH
H
HH
Valence #
2-regularity #
This can be
avoided by
learning HRG from
data [Aguiñaga+, 16]
Use an irredundant
tree decomposition
(our contribution)](https://image.slidesharecdn.com/20191120ibis-191120000917/85/Graph-generation-using-a-graph-grammar-39-320.jpg)

![© 2019 IBM Corporation
/52
A naive application of the existing algorithm doesn’t work
§Naive application of the HRG inference algorithm [Aguiñaga+, 16]
–Input: Set of hypergraphs
–Output: HRG w/ the following properties:
• All the input hypergraphs are in the language $
• Guarantee the valence conditions $
• No guarantee on 2-regularity %
42
MHG inference algorithm
C C
H
H
HH
H
HH
This cannot be transformed
into a molecular graph](https://image.slidesharecdn.com/20191120ibis-191120000917/85/Graph-generation-using-a-graph-grammar-41-320.jpg)
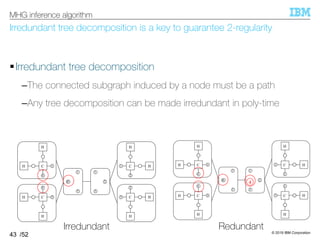
![© 2019 IBM Corporation
/52
MHG inference algorithm is different from the existing one by two steps
§MHG Inference algorithm [Kajino, 19]
–Input: Set of molecular graphs
–Output: MHG w/ the following properties:
• All the input hypergraphs are in the language $
• Guarantee the valence conditions $
• Guarantee 2-regularity &
44
MHG inference algorithm
1. Convert molecular graphs into molecular hypergraphs
2. Compute tree decompositions of molecular hypergraphs
3. Convert each tree decomposition to be irredundant
4. Extract production rules
5. Compose MHG by taking their union
Thanks to HRG
Our contribution](https://image.slidesharecdn.com/20191120ibis-191120000917/85/Graph-generation-using-a-graph-grammar-43-320.jpg)

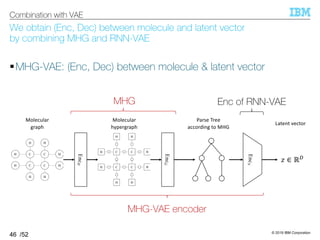
![© 2019 IBM Corporation
/52
First, we learn (Enc, Dec) between a molecule and its vector
representation using MHG-VAE
§Global molecular optimization [Gómez-Bombarelli+, 16]
–Find: Molecule that maximizes the target
–Method: VAE+BO
1. Obtain MHG from the input molecules
2. Train RNN-VAE on syntax trees
3. Obtain vector representations f. ∈ ℝh
.i%
)
1. Some of which have target values {j. ∈ ℝ}
4. BO gives us candidates fk ∈ ℝh
ki%
l that may maximize the target
5. Decode them to obtain molecules !k ki%
l
47
Combination with VAE
Image from [Gómez-Bombarelli+, 16]](https://image.slidesharecdn.com/20191120ibis-191120000917/85/Graph-generation-using-a-graph-grammar-46-320.jpg)
![© 2019 IBM Corporation
/52
Given vector representations and their target values,
we use BO to obtain a vector that optimizes the target
§Global molecular optimization [Gómez-Bombarelli+, 16]
–Find: Molecule that maximizes the target
–Method: VAE+BO
1. Obtain MHG from the input molecules
2. Train RNN-VAE on syntax trees
3. Obtain vector representations f. ∈ ℝh
.i%
)
1. Some of which have target values {j. ∈ ℝ}
4. BO gives us candidates fk ∈ ℝh
ki%
l that may maximize the target
5. Decode them to obtain molecules !k ki%
l
48
Combination with VAE
Image from [Gómez-Bombarelli+, 16]](https://image.slidesharecdn.com/20191120ibis-191120000917/85/Graph-generation-using-a-graph-grammar-47-320.jpg)
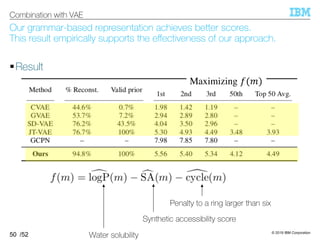
![© 2019 IBM Corporation
/52
We evaluate the benefit of our grammar-based representation,
compared with existing ones
§Empirical study
–Purpose: How much does our representation facilitate VAE training?
–Baselines:
• {C,G,SD}VAE use SMILES (text repr.)
• JT-VAE assembles molecular components
– It requires NNs other than VAE for scoring
–Tasks:
• VAE reconstruction
• Valid prior ratio
• Global molecular optimization
49
Combination with VAE
Image from [Jin+, 18]](https://image.slidesharecdn.com/20191120ibis-191120000917/85/Graph-generation-using-a-graph-grammar-48-320.jpg)

![© 2019 IBM Corporation
/52
[Aguiñaga+, 16] Aguiñaga, S., Palacios, R., Chiang, D., and Weninger, T.: Growing graphs from hyperedge
replacement graph grammars. In Proceedings of the 25th ACM International on Conference on Information and
Knowledge Management, pp. 469–478, 2016.
[Feder, 71] Feder, J: Plex languages. Information Sciences, 3, pp. 225-241, 1971.
[Gómez-Bombarelli+, 16] Gómez-Bombarelli, R., Wei, J. N., Duvenaud, D., Hernández-Lobato, J. M., Sánchez-
Lengeling, B., Sheberla, D., Aguilera-Iparraguirre, J., Hirzel, T. D., Adams, R. P., and Aspuru-Guzik, A.: Automatic
chemical design using a data-driven continuous representation of molecules. ACS Central Science, 2018. (ArXiv ver.
appears in 2016)
[Jin+, 18] Jin, W., Barzilay, R., and Jaakkola, T.: Junction tree variational autoencoder for molecular graph generation.
In Proceedings of the Thirty-fifth International Conference on Machine Learning, 2018.
[Kajino, 19] Kajino, H.: Molecular hypergraph grammar with its application to molecular optimization. In Proceedings of
the Thirty-sixth International Conference on Machine Learning, 2019.
[Pavlidis, 72] Pavlidis, T.: Linear and context-free graph grammars. Journal of the ACM, 19(1), pp.11-23, 1972.
[You+, 18] You, J., Liu, B., Ying, Z., Pande, V., and Leskovec, J.: Graph convolutional policy network for goal-directed
molecular graph generation. In Advances in Neural Information Processing Systems 31, pp. 6412–6422, 2018.
.
52
References](https://image.slidesharecdn.com/20191120ibis-191120000917/85/Graph-generation-using-a-graph-grammar-51-320.jpg)