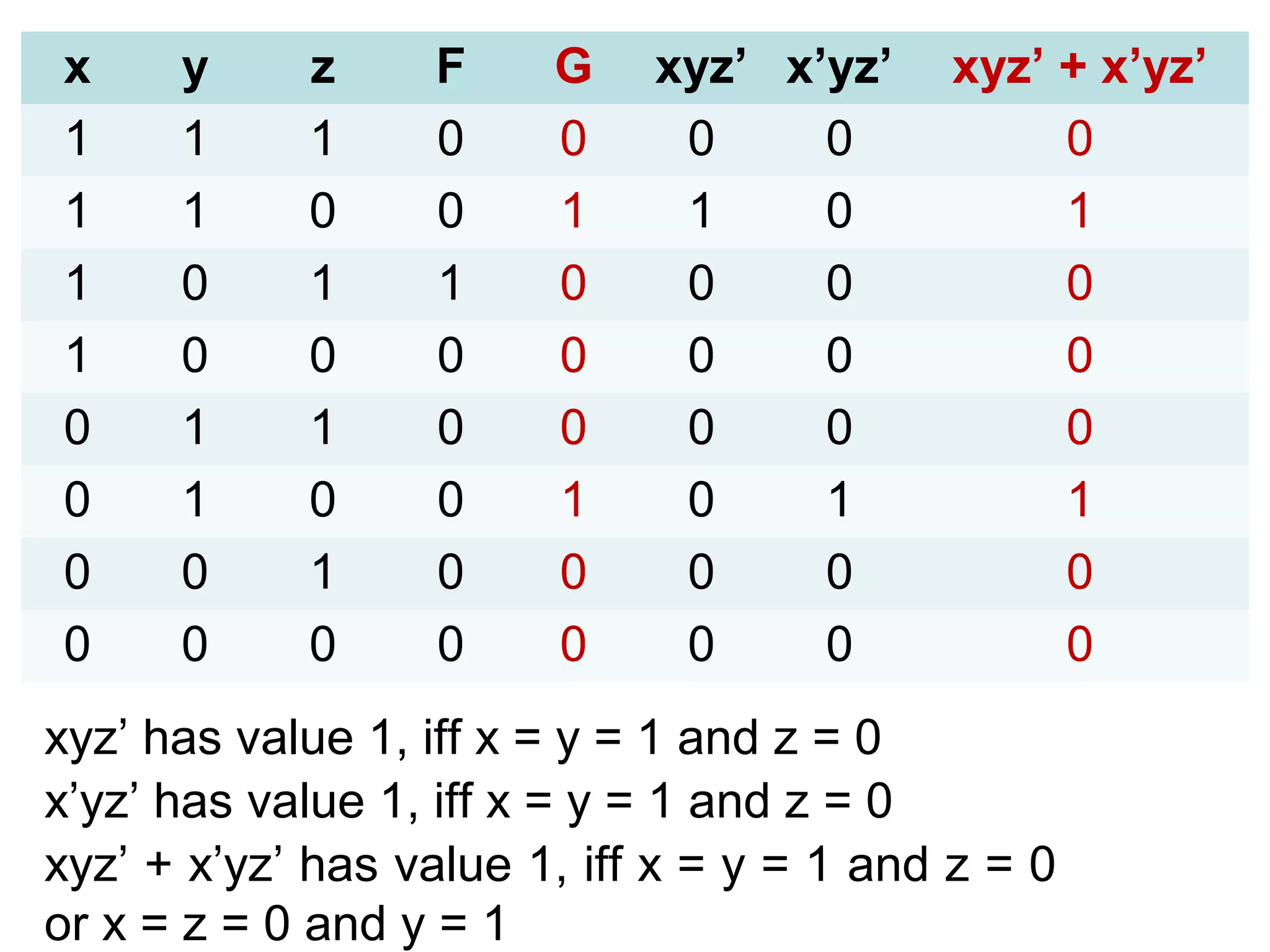
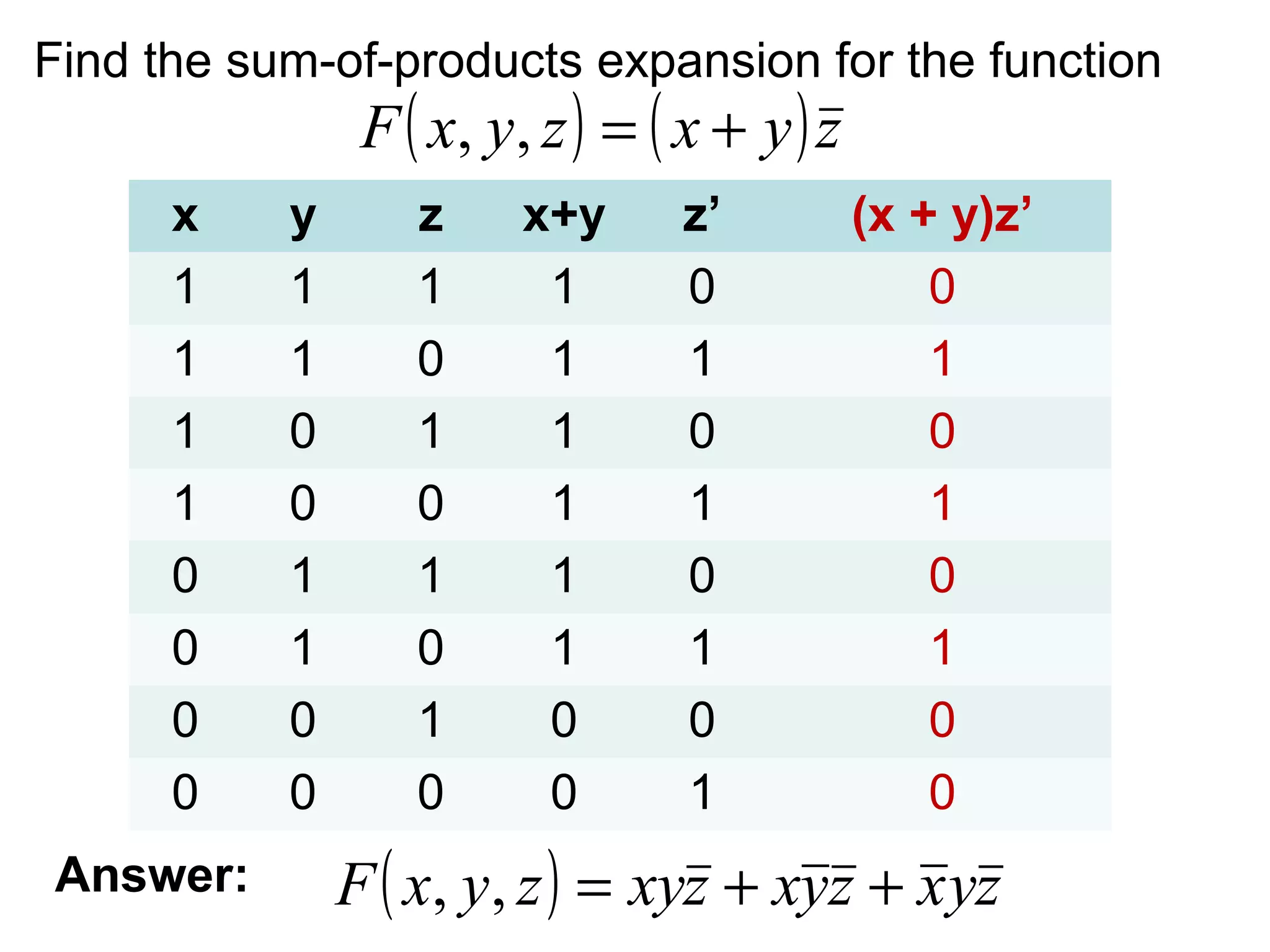
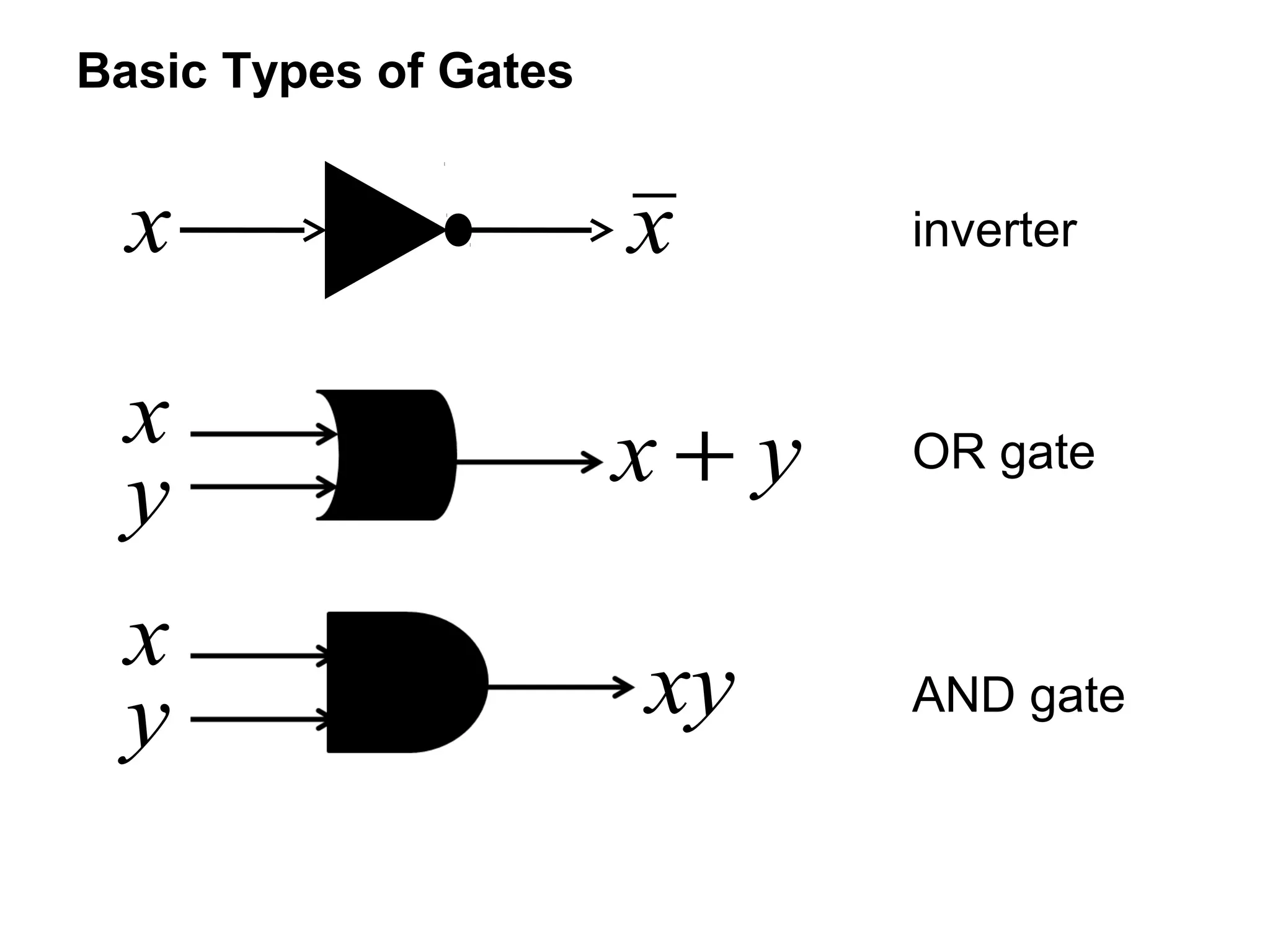
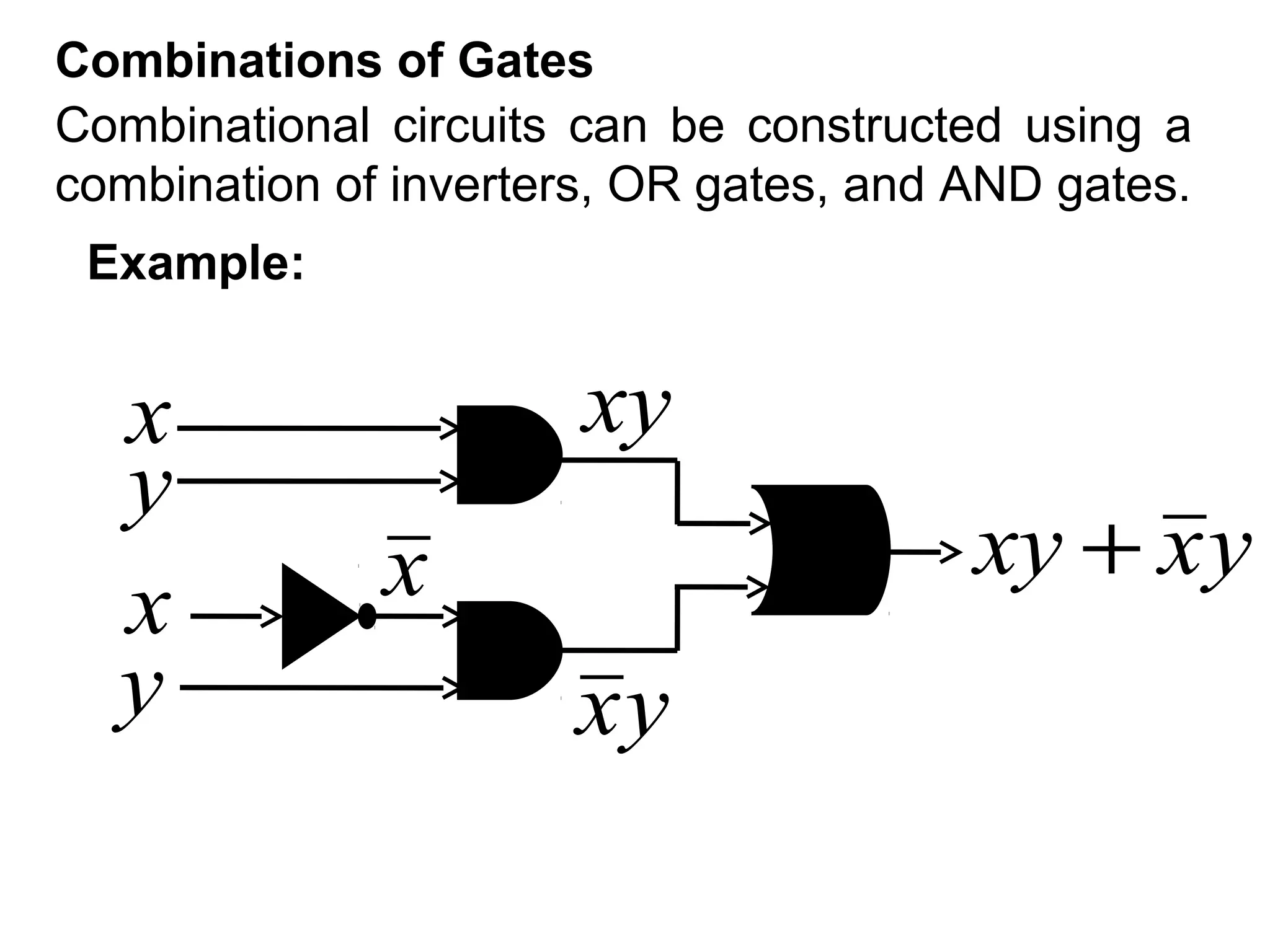
This document provides an overview of Boolean expressions and Boolean functions. It defines Boolean variables and Boolean functions, and how Boolean expressions are recursively defined using 0, 1, variables, and operators. It discusses Boolean operators like AND, OR, and their truth tables. It also covers Boolean identities and laws like commutative, associative, distributive, etc. Additionally, it discusses Boolean normal forms, logic gates, combinational circuits, and provides examples of representing and simplifying Boolean functions and expressions.

1. Boolean Expressions and Boolean Functions
Let B = {0, 1}. The variable x is called a Boolean
variable if it assumes values only from B. A function
Bn, the set {(x1, x2, ….xn)|xi ε B, 1 ≤ i ≤ n}, to B is
called a Boolean function of degree n
x y F(x, y)
1 1
0
The values of Boolean function.
1 0
1
0 1
0
0 0
0
The Boolean expressions in the variables x1, x2,
…,xn are defined recursively as follows:
0, 1, x1, x2, ….., xn

2. Example: Find the values of the Boolean function
represented by F ( x, y, z ) = xy + z
x
1
1
1
1
0
0
0
0
y
1
1
0
0
1
1
0
0
z
1
0
1
0
1
0
1
0
xy
1
1
0
0
0
0
0
0
z’
0
1
0
1
0
1
0
1
xy + z’
1
1
0
1
0
1
0
1

3. The Boolean functions F and G of n variables are
equal if and only if F(b1, b2, …, bn) = G(b1, b2, …,bn)
whenever b1, b2, …, bn belong to B. Two different
Boolean expressions that represent the same
function are called equivalent.
ex: xy, xy + 0, and (xy)1
The complement of the Boolean function F is the
function
F , where
F ( x1 ,  , xn ) = F ( x1 ,  xn )

4. The Boolean sum F + G and the Boolean product
FG are defined by
(F + G)(x1,…., xn) = F(x1,…, xn) + G(x1,…, xn),
(FG)(x1,…, xn) = F(x1,…, xn)G(x1,…, xn)
The Boolean functions of degree 2
x
y
F1
F2
F3
F4
F5
F6
F7
F8
F9
F10 F11 F12 F13 F14 F15 F16
1
1
0
0
1
0
1
0
1
1
1
1
1
1
1
0
1
1
0
1
1
1
0
0
1
0
1
1
1
0
1
0
1
0
0
1
1
0
0
0
0
1
1
1
0
1
1
0
0
1
0
1
0
1
0
0
0
0
1
1
0
0
1
0
0
0
0
1
0
0
0
0
To determine the number of different Boolean functions
of degree n, we use the formula: 22n

5. Identities of Boolean Algebra
Identity
Name
x=x
Law of double complement
x+x = x
x.x = x
x +0 = x
x.1 = x
x +1 =1
x.0 = 0
x+ y = y+ x
xy = yx
Idempotent Laws
Identity Laws
Dominance Laws
Commutative Laws

6. Identities of Boolean Algebra
Identity
x + ( y + z) = ( x + y) + z
x( yz ) = ( xy ) z
Name
Associative Laws
x + yz = ( x + y )( x + z )
x( y + z ) = xy + xz
Distributive Laws
( xy ) = x + y
( x + y ) = xy
De Morgan’s Laws

7. Example: Show that the distributive law
x(y + z) = xy + xz is valid
x
y
z
y+z
xy
xz
1
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
0
1
1
1
0
1
1
1
0
1
1
0
0
0
0
0
0
1
0
1
0
0
0
0
0
x(y+z) xy+xz
1
1
1
0
0
0
0
0
1
1
1
0
0
0
0
0

8. Duality
The dual of a Boolean expression is obtained by
interchanging Boolean sums and Boolean products
and interchanging 0s and 1s.
Find the duals of
Answer:
x( y + 0 ) and
x .1 + ( y + z ) .
x + ( y.1) and
( x + 0)( yz )

9. Note:
The dual of the Boolean function F, denoted by
Fd, represented by a Boolean expression is the function
represented by the dual of this expression. This dual
function does not depend on the particular Boolean
expression used to represent F. An identity between
functions represented by Boolean expressions remains
valid when the duals of both sides of the identity are
taken. This result, called the duality principle, is
useful for obtaining new identities.

10. A Boolean algebra is a set B with two binary
operations v and ʌ, elements 0 and 1, and unary
operation ¬ such that the following properties hold
for all x, y, and z in B:
x ∨ 0 = x

x ∧1 = x 
Identity Laws
x ∨ x =1

x ∧ x = 0
Domination Laws

11. x ∨ y = y ∨ x

x ∧ y = y ∧ x
Commutative Laws
( x ∨ y) ∨ z = x ∨ ( y ∨ z)

( x ∧ y) ∧ z = x ∧ ( y ∧ z)
Associative Laws
x ∨ ( y ∧ z) = ( x ∨ y) ∧ ( x ∨ z)

x ∧ ( y ∨ z) = ( x ∧ y) ∨ ( x ∧ z)
Distributive Laws

12. Representing Boolean Functions
Find Boolean expressions that
functions F(x, y, z) and G(x, y, z)
x
1
1
1
1
0
0
0
0
y
1
1
0
0
1
1
0
0
z
1
0
1
0
1
0
1
0
F
0
0
1
0
0
0
0
0
G
0
1
0
0
0
1
0
0
represent
the
To represent F, the value is
1 when x = z = 1 and y = 0
or xy’z.
To represent G, the value is
1 when x = y = 1 and z = 0
or when x = z = 0 and y =1.
We can form an expression
with these values by taking
the Boolean sum of two
different Boolean products.

13. x
1
1
1
1
0
0
0
0
y
1
1
0
0
1
1
0
0
z
1
0
1
0
1
0
1
0
F
0
0
1
0
0
0
0
0
G
0
1
0
0
0
1
0
0
xyz’ x’yz’
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
xyz’ + x’yz’
0
1
0
0
0
1
0
0
xyz’ has value 1, iff x = y = 1 and z = 0
x’yz’ has value 1, iff x = y = 1 and z = 0
xyz’ + x’yz’ has value 1, iff x = y = 1 and z = 0
or x = z = 0 and y = 1

14. A literal is a Boolean variable or its complement. A
minterm of the Boolean variables x1, x2, …, xn is a
Boolean product y1, y2, …, yn, where yi = xi or yi = x’i.
Hence, a minterm is a product of n literals, with one
literal for each variable.
Example: Find a minterm that equals 1 if x 1 = x3 = 0
and x2 = x4 = x5 = 1, and equals 0 otherwise.
x1 x2 x3 x4 x5
The minterm showed has the
correct set of values.

15. Sum-of-products expansion or the disjunctive
normal form of the Boolean function is the sum of
minterms that represents a function. A Boolean sum
of minterms has the value 1 when exactly one of the
minterms in the sum has the value 1.
It is also possible to find a Boolean expression that
represents a Boolean function by taking a Boolean
product of Boolean sums. The resulting expansion is
called the conjunctive normal form or product-ofsums expansion of the function. These expansions
can be found from sum-of-products expansion by
taking their duals.

16. Find the sum-of-products expansion for the function
F ( x, y , z ) = ( x + y ) z
x
1
1
1
1
0
0
0
0
Answer:
y
1
1
0
0
1
1
0
0
z
1
0
1
0
1
0
1
0
x+y
1
1
1
1
1
1
0
0
z’
0
1
0
1
0
1
0
1
(x + y)z’
0
1
0
1
0
1
0
0
F ( x, y, z ) = xyz + xyz + x yz

17. Logic Gates
Gates are the basic elements of circuits.
Combinatorial circuits or gating networks are
circuits have no memory capabilities. These circuits
give output that depends only on the input, and not
on the current state of the circuit.
Types of Elements
Inverter which accepts the value of one Boolean
variable as input and produces the complement of
this value as output.
OR Gate, the inputs are the values of two or more
Boolean variables. The output is the Boolean sum of
their values.
AND Gate, the inputs are the values of two or more
Boolean variables. The output is the Boolean
product of their values.

18. Basic Types of Gates
x
x
x
y
x+y
x
y
xy
inverter
OR gate
AND gate

19. Combinations of Gates
Combinational circuits can be constructed using a
combination of inverters, OR gates, and AND gates.
Example:
x
y
x
y
xy
xy + x y
x
xy

20. Exercises:
1.Find the Boolean product of the Boolean variables
x, y, and z, or their complements, that has the value
1 if and only if
a. x =y = 0, z = 1
b. x = z = 0, y = 1
c. x = 0, y = z = 1
d. x = y = z = 0
2. Find the sum-of-products expansions of the
following Boolean functions.
a ) F ( x, y , z ) = x + y + z
b ) F ( x, y , z ) = ( x + z ) y
c) F ( x, y, z ) = x + yz
d ) F ( x, y, z ) = xy + z

21. Exercises:
Construct circuits that produce the following
outputs:
1)( x + y ) x
2) x ( y + z )
3)( x + y + z )( x yz )