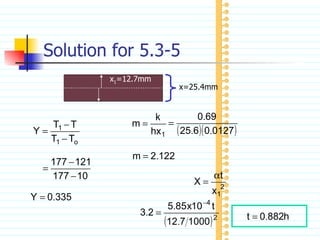
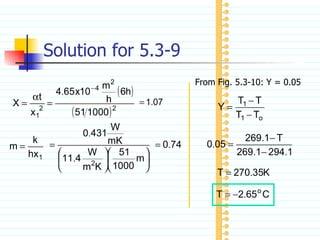
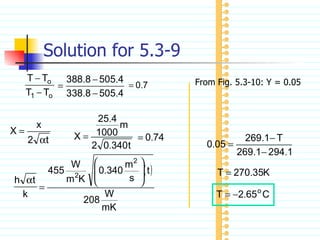
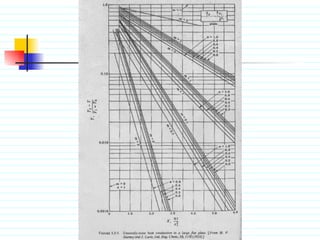
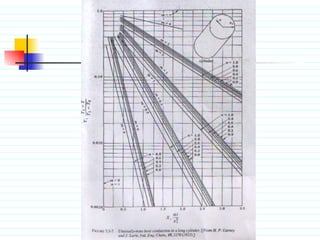
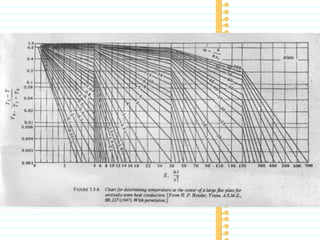
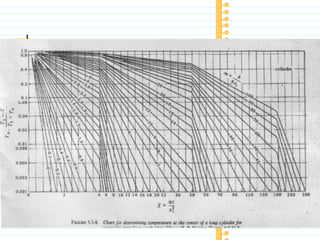
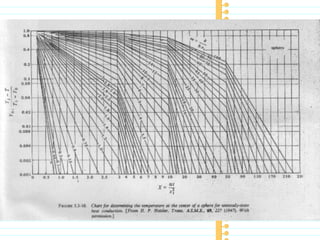
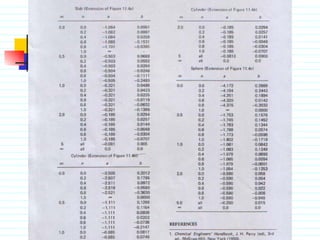
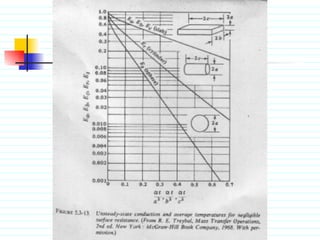
The document discusses unsteady state heat conduction, which occurs when the temperature gradient across a solid changes over time. It provides examples of unsteady state conduction and examines the one-dimensional case. It introduces the governing equation and describes using charts like the Geankoplis charts to solve problems involving startup conditions for plates, cylinders, and spheres. It then provides examples of using the charts to solve problems involving cooling/heating of various objects.

1. Unsteady State Conduction Evelyn R. Laurito Lani Pestano Ch.E. 206

2. Lecture Objectives To understand the concept of unsteady state conduction To study the case of unidirectional unsteady state conduction To understand how to use Geankoplis Charts in solving unidirectional unsteady state conduction problems Gurney and Lurie Charts Heisler Chart Chart for Average Temperature Chart for Semiinfinite solid To understand how to use Numerical Methods in solving unidirectional unsteady state conduction problems

3. Unsteady State Conduction This happens when the temperature gradient across the solid changes with time. This may be due to unstable boundary temperatures at startup, sudden temperature fluctuations during steady state conditions, or internal generation of heat. Sample Cases: Startup of a Furnace Heat Treatment of Solids Deep Oil Frying Change of Weather

4. Unidirectional Unsteady State Case  x  y  z x x+  x q in q out A = V = Solid properties:  , c P Mass = Heat Balance Across  x: q in - q out = Rate of heat accumulation Rate of heat accumulation = Using Fourier’s Law: q in = q out = c P  y  z  x  y  z  x  y  z   x  y  z   T  t - k  y  z  T  x x - k  y  z  T  x x +  x

5. Unidirectional Unsteady State Case The Heat Balance becomes: - = Simplifying: -  x From Calculus: Final Equation:  but - k  y  z  T  x x - k  y  z  T  x x +  x  x  y  z  c P  T  t  T  t = k  c P  T  x x +  x  T  x x  T  x x +  x -  T  x x  x =  2 T  x 2  T  t = k  c P =  2 T  x 2 

6. Unidirectional Unsteady State Case Depends on solid geometry Requires PDE solution methods that results into Fourier series solutions that are tedious to evaluate May be simplified by the use of charts or numerical methods Use of Charts: Gurnie-Lurie Charts – to determine point temperatures Heisler Charts – to determine central temperatures Average Temperature Chart Chart for Semiinfinite Solids  T  t =  2 T  x 2  Solution of:

7. Geankoplis Charts Gurney-Lurie Charts Fig. 5.3-5/340 for large flat plate Fig. 5.3-7/343 for long cylinder Fig. 5.3-9/345 for sphere Heisler Chart Fig. 5.3-6/341 for large flat plate Fig. 5.3-8/344 for long cylinder Fig. 5.3-10/346 for sphere Fig. 5.3-13/349 for Ave. Solid Temperature Fig. 5.3-3/337 for Semi-infinite solid

8. Nomenclature Gurney-Lurie and Heisler Charts: T o = temperature at t(time)= 0 (uniform) T 1 = new and constant surface temperature x 1 = ½ plate thickness, outer radius of cylinder or sphere  = constant thermal diffusivity X =  t/ x 1 2 : relative time x = distance from plate center or any radius of a cylinder or a sphere n = x/x 1 : relative position T = point temperature at position x and time t Y = (T 1 -T)/(T 1 -T o ) :unaccomplished temp. change h = convective heat transfer coefficient m = k/(hx 1 ) : relative resistance

9. Nomenclature Average Temperature Chart T o = temperature at t(time)= 0 (uniform) T 1 = new and constant surface temperature T av = average solid temperature at time t E = (T 1 -T av )/(T 1 -T o ) a = ½ plate thickness, outer radius of cylinder or sphere b = ½ plate width c = ½ plate length, ½ cylinder length

10. Nomenclature Chart for Semi-infinite solid Semi-infinite solid – solid where the unidirectional conductive heat transfer is infinite (Ex. Ground) T o = initial uniform solid temperature T 1 = constant ambient temperature to which solid surface is exposed T = temperature of solid at position x 1- Y = (T-T o )/(T 1 -T o ): Ordinate h(  t) 0.5 /k : convective parameter x/[2 (  t) 0.5 ]: Abscissa

11. Problems from Geankoplis Exercises: 5.3-5 (Plate) 5.3-7 (Long Cylinder) 5.3-9 (Sphere) Find the average solid temperature for all of the above cases 5.3-3 Homework: Geankoplis: 5.3-2;5.3-4;5.3-6;5.3-8;5.3-10 (pages 375-377) Foust: 11.18;11.20;11.21(page 231)

12. 5.3-5 Cooling a Slab of Meat A slab of meat 25.4 mm thick originally at a uniform temperature of 10 o C is to be cooked from both sides until the center reaches 121 o C in an oven at 177 o C. The convection coefficient can be assumed constant at 25.6 W/m 2 -K. Neglect any latent heat changes and calculate the time required. The thermal conductivity is 0.69 W/m-K and the thermal diffusivity 5.85x10 -4 m 2 /h.

13. Solution for 5.3-5 Given: t= 25.4 mm T o =10 o C T=121 o C (Center T) at x 1 T 1 =177 o C h=25.6 W/m 2 -K k=0.69 W/m-K  =5.85x10 -4 m 2 /h Required: t= ?

14. Solution for 5.3-5 x 1 =12.7mm x=25.4mm

15. 5.3-7 Cooling of a Steel Rod A long steel rod 0.305 m in diameter is initially at a temperature of 588K. It is immersed in an oil bath maintained at 311K. The surface convective coefficient is 125 W/m 2 -K. Calculate the temperature at the center of the rod after 1 h. The average physical properties of the steel are k=38 W/m-K and  =0.0381m 2 /h

16. Solution for 5.3-7 Given: D= 0.305 m T o =588 K T 1 =311 K h=125 W/m 2 -K t=1 h k=38 W/m-K  =0.0381 m 2 /h Required: T at the center

17. Solution for 5.3-7

18. 5.3-9 Temp. of Oranges on Trees During Freezing Weather In orange-growing areas, the freezing of the oranges on the trees during cold nights is economically important. If the oranges are initially at a temperature of 21.1 o C, calculate the center temperature of the orange if exposed to air at –3.9 o C for 6 h. The oranges are 102 mm in diameter and the convective coefficient is estimated as 11.4W/m 2 -K. The thermal conductivity k is 0.431 W/m-K and  =4.65x10 -4 m 2 /h. Neglect any latent heat effects.

19. Solution for 5.3-9 Given: D= 102 m  x=102/2=51mm T o =21.1 o C=294.1K T 1 =-3.9 o C=269.1K h=11.4 W/m 2 -K t=6 h k=0.431 W/m-K  =4.65x10 -4 m 2 /h Required: T at the center

20. Solution for 5.3-9 From Fig. 5.3-10: Y = 0.05

21. 5.3-3 Cooling a Slab of Aluminum A large piece of aluminum that can be considered a semi-infinite solid initially has a uniform temperature of 505.4K. The surface is suddenly exposed to an environment at 338.8K with a surface convection coefficient of 455W/m 2 -K. Calculate the time in hours for the temperature to reach 388.8 K at a depth of 25.4 mm. The average physical properties are  =0.340m 2 /h and k=208W/m-K.

22. Solution for 5.3-3 Given: D= 0.305 m T o =505.4 K T 1 =338.8 K T=388.8K when x=25.4mm h=455 W/m 2 -K k=208 W/m-K  =0.304 m 2 /h Required: time in hours for the temperature to reach 388.8K at a depth of 25.4 mm

23. Solution for 5.3-9 From Fig. 5.3-10: Y = 0.05