Download as PDF, PPTX
Uploaded byDirek Boonturm
Cavity resonator
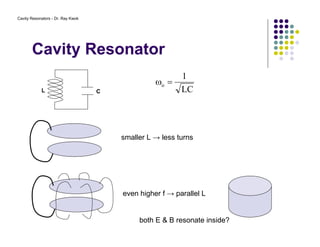
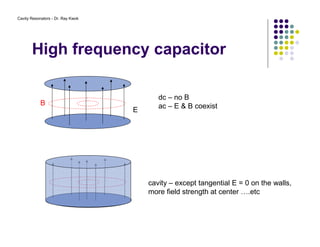
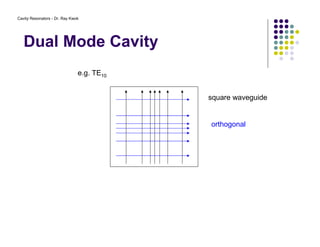
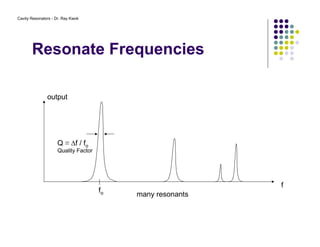
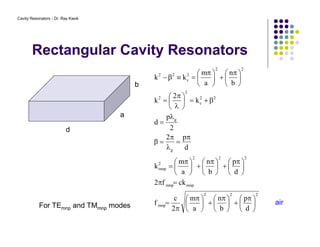
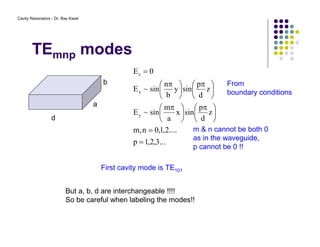
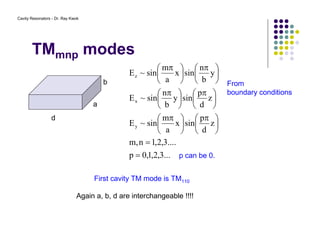
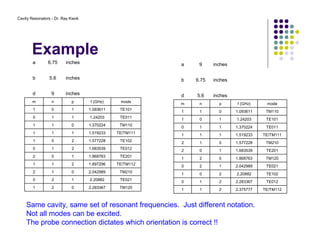
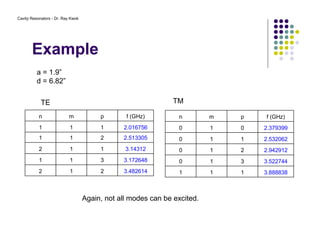
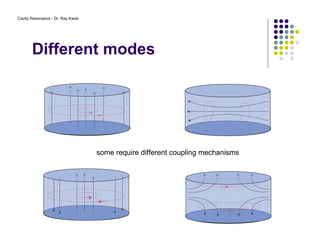
1. Cavity resonators confine electromagnetic waves inside hollow structures such as rectangular boxes or cylindrical cans through resonance. 2. The resonant modes inside the cavity depend on its geometry and are determined by solving Maxwell's equations with the appropriate boundary conditions. 3. Common modes include TE and TM, where the electric and magnetic fields are transverse to the axis of propagation. 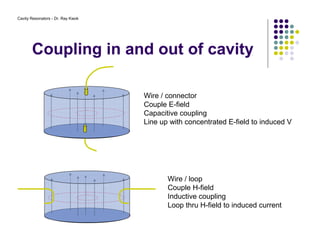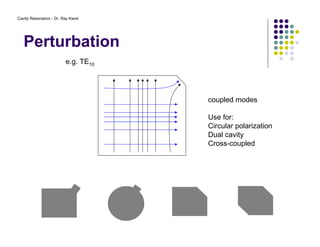4. Coupling mechanisms such as wires or loops are used to input and output power to selectively excite specific resonant modes within the cavity.
![3_Antenna Array [Modlue 4] (1).pdf](https://cdn.slidesharecdn.com/ss_thumbnails/3antennaarraymodlue41-220419112111-thumbnail.jpg?width=640&height=640&fit=bounds)
Cavity resonator
- 1. Cavity Resonators Microwave Engineering EE172 Dr. Ray Kwok Reference: Feynman, Lectures on Physics, Vol 2
- 2. Cavity Resonators -Dr. Ray Kwok LC Resonator (Lenz’s Law)
- 3. Cavity Resonators -Dr. Ray Kwok Helical Resonator L C LC 1 o =ω Higher frequency → smaller L or C L C smaller C → smaller area Just the coil itself – resonate (Helical Resonator) Internal capacitance between turns Can’t use coil in very high frequency L C R real coil equivalent
- 4. Cavity Resonators -Dr. Ray Kwok Cavity Resonator L C LC 1 o =ω smaller L → less turns even higher f → parallel L both E & B resonate inside?
- 5. Cavity Resonators -Dr. Ray Kwok High frequency capacitor dc – no B ac – E & B coexist E B cavity – except tangential E = 0 on the walls, more field strength at center ….etc
- 6. Cavity Resonators -Dr. Ray Kwok Coupling in and out of cavity Wire / connector Couple E-field Capacitive coupling Line up with concentrated E-field to induced V Wire / loop Couple H-field Inductive coupling Loop thru H-field to induced current
- 7. Cavity Resonators -Dr. Ray Kwok Resonate Frequencies f output fo Q ≡ ∆f / fo Quality Factor many resonants
- 8. Cavity Resonators -Dr. Ray Kwok Different modes some require different coupling mechanisms
- 9. Cavity Resonators -Dr. Ray Kwok Rectangular Cavity Resonators a b d 222 mnp mnpmnp 222 2 mnp g g 22 c 2 2 22 2 c 22 d p b n a m 2 c f ckf2 d p b n a m k d p2 2 p d k 2 k b n a m kk π + π + π π = =π π + π + π = π = λ π =β λ = β+= λ π = π + π =≡β− airFor TEmnp and TMmnp modes
- 10. Cavity Resonators -Dr. Ray Kwok TEmnp modes a b d ...3,2,1p ....2,1,0n,m z d p sinx a m sin~E z d p siny b n sin~E 0E y x z = = π π π π = m & n cannot be both 0 as in the waveguide, p cannot be 0 !! First cavity mode is TE101 But a, b, d are interchangeable !!!! So be careful when labeling the modes!! From boundary conditions
- 11. Cavity Resonators -Dr. Ray Kwok TMmnp modes a b d ...3,2,1,0p ....3,2,1n,m z d p sinx a m sin~E z d p siny b n sin~E y b n sinx a m sin~E y x z = = π π π π π π p can be 0. First cavity TM mode is TM110 Again a, b, d are interchangeable !!!! From boundary conditions
- 12. Cavity Resonators -Dr. Ray Kwok Example TM1202.283367021 TE0212.20882120 TM2102.042989012 TE/TM1121.897296211 TE2011.868763102 TE0121.683539210 TE1021.577228201 TE/TM1111.519233111 TM1101.370224011 TE0111.24203110 TE1011.093611101 modef (GHz)pnm inches9d inches5.6b inches6.75a TE/TM1122.375777211 TE0122.283367210 TE1022.20882201 TE0212.042989120 TM1201.868763021 TE2011.683539102 TM2101.577228012 TE/TM1111.519233111 TE0111.370224110 TE1011.24203101 TM1101.093611011 modef (GHz)pnm inches5.6d inches6.75b inches9a Same cavity, same set of resonant frequencies. Just different notation. Not all modes can be excited. The probe connection dictates which orientation is correct !!
- 13. Cavity Resonators -Dr. Ray Kwok Cylindrical Cavity Resonators 2 2 cnmp 2 2 c 2 nmp g 22 c 2 2 d p k 2 c f d p kk d p2 k 2 k π + π = π += π = λ π =β β+= λ π = air a d e.g. Coke can, a ~ 1.25”, d ~ 5” TE111: kc = 1.8412 / 1.25 = 1.473 GHz01.3 5 1 )473.1( 2 811.11 f 2 2 111 = π + π =
- 14. Cavity Resonators -Dr. Ray Kwok TEnmp modes ...3,2,1p 0)ak(J z d p sin)k(J)nsinBncosA(~E z d p sin)k(J)nsinBncosA(~E 0E nm ' n c ' n cn z = = π ρφ+φ π ρφ−φ = φ ρ a d From boundary conditions. p starts from 1 First TE cavity mode is TE111.
- 15. Cavity Resonators -Dr. Ray Kwok TMnmp modes ...3,2,1,0p 0)ak(J z d p sin)k(J)nsinBncosA(~E z d p sin)k(J)nsinBncosA(~E z d p cos)k(J)nsinBncosA(~E nmn cn c ' n c ' nz = = π ρφ−φ π ρφ+φ π ρφ+φ φ ρ a d From boundary conditions. p begins at 0. First TM cavity mode “usually” is TM011. p = 0 means Er and Eρ = 0 !!! And cannot be excited with connector on the sides!
- 16. Cavity Resonators -Dr. Ray Kwok Example 3.482614212 3.172648311 3.14312112 2.513305211 2.016756111 f (GHz)pmn a = 1.9” d = 6.82” TE 3.888838111 3.522744310 2.942912210 2.532062110 2.379399010 f (GHz)pmn TM Again, not all modes can be excited.
- 17. Cavity Resonators -Dr. Ray Kwok Resonant e.g. Coke can, a ~ 1.25”, d ~ 5” TE111: kc = 1.8412 / 1.25 = 1.473 GHz01.3 5 1 )473.1( 2 811.11 f 2 2 111 = π + π =
- 18. Cavity Resonators -Dr. Ray Kwok Dual Mode Cavity e.g. TE10 orthogonal square waveguide
- 19. Cavity Resonators -Dr. Ray Kwok Perturbation e.g. TE10 coupled modes Use for: Circular polarization Dual cavity Cross-coupled
- 20. Cavity Resonators -Dr. Ray Kwok Dual Mode TE111 mode Up to 5-modes cavity has been demonstrated in a spherical cavity.