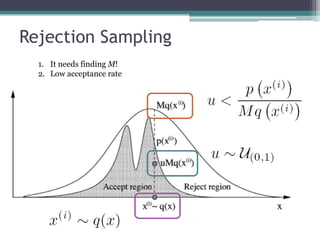
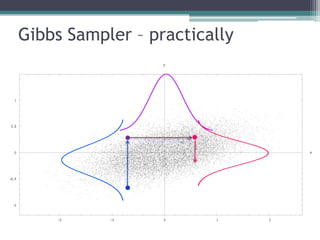
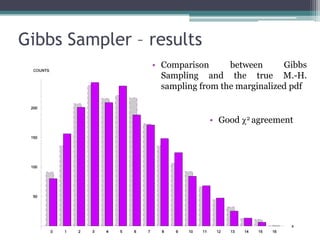
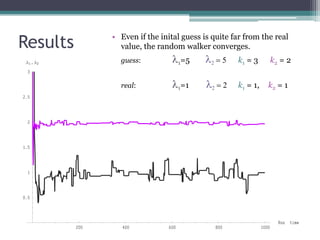
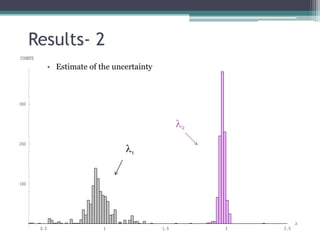
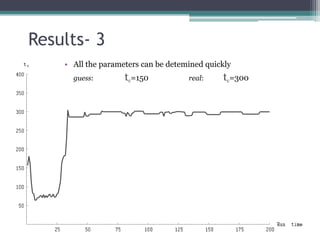
1) Markov Chain Monte Carlo (MCMC) methods use Markov chains to sample from complex probability distributions and are useful for problems that cannot be solved efficiently using other methods. 2) Common MCMC algorithms include Metropolis-Hastings, which samples from a target distribution using a proposal distribution, and Gibbs sampling, which efficiently samples multidimensional distributions by updating variables sequentially. 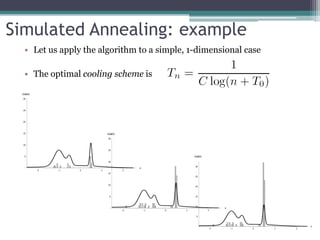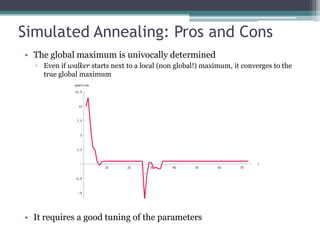3) MCMC methods like simulated annealing can find global maxima of probability distributions and have applications in statistical mechanics, optimization, and Bayesian inference.

1. MarkovChainMonteCarlo
theory and worked examples
Dario Digiuni,
A.A. 2007/2008

2. Markov Chain Monte Carlo
• Class of sampling algorithms
• High sampling efficiency
• Sample from a distribution with unknown normalization constant
• Often the only way to solve problems in time polynomial in the
number of dimensions
e.g. evaluation of a convex body volume

3. MCMC: applications
• Statistical Mechanics
Metropolis-Hastings
• Optimization
▫ Simulated annealing
• Bayesian Inference
▫ Metropolis-Hastings
▫ Gibbs sampling

4. The Monte Carlo principle
• Sample a set of N independent and identically-distributed variables
• Approximation of the target p.d.f. with the empirical expression
… then approximation of the integrals!

5. Rejection Sampling
1. It needs finding M!
2. Low acceptance rate

6. Idea
• I can use the previously sampled value to find the following one
• Exploration of the configuration space by means of Markov Chains:
def .: Markov process
def .: Markov chain

7. Invariant distribution
• Stability conditions:
1. Irreducibility= for every state there exists a finite probability to visit
any other state
2. Aperiodicity = there are no loops.
• Sufficient condition
1. Detailed balance principle
MCMC algorithms are aperiodic, irreducible Markov chains having
the target pdf as the invariant distribution

8. Example
• What is the probability to find the lift at the ground floor in a three
floor building?
▫ 3 states Markov chain
▫ Lift= Random Walker
▫ Transition matrix
▫ Looking for the invariant distribution
… burn-in …

9. Example - 2
• I can apply the matrix T on the right to any of the states, e.g.
homogeneous
Markov chain
~ 50% is the probability to find
• Google’s PageRank: the lift at the ground floor
▫ Websites are the states, T is defined by the number of hyperlinks among
them and the user is the random walker:
 The webpages are displayed following the invariant distribution!

10. Metropolis-Hastings
• Given the target distribution
equivalent to T
1. Choose a value for
2. Sample from a proposal distribution
3. Accept the new value with probability
4. Return to 1
Ratio independent Equal in Metropolis algorithm
of the normalization!

11. M.-H. – Pros and Cons
• Very general sampling method:
▫ I can sample from a unnormalized distribution
▫ It does not require to provide upper bound for the function
• Good working depends on the choice of the proposal distribution
▫ well-mixing condition

12. M.-H. - Example
• In Statistical Mechanics it is important to evalue the partition
function,
e.g. Ising model
Sum every possible spin state:
In a 10 x 10 x 10 spin cube,
I would have to sum over
MCMC APPROACH:
1. Evaluate the system’s energy Possible states = UNFEASIBLE
2. Pick up a spin at random and flip it:
1. If energy decreases, this is the new spin configuration
2. If energy increases, this is the new spin configuration with
probability

13. Simulated Annealing
• It allows one to find the global maximum of a generic pdf
▫ No comparison between the value of local minima required
▫ Application to the maximum-likelihood method
• It is a non-homogeneous Markov chain whose invariant distribution
keeps changing as follows:

14. Simulated Annealing: example
• Let us apply the algorithm to a simple, 1-dimensional case
• The optimal cooling scheme is

15. Simulated Annealing: Pros and Cons
• The global maximum is univocally determined
▫ Even if walker starts next to a local (non global!) maximum, it converges to the
true global maximum
• It requires a good tuning of the parameters

16. Gibbs Sampler
• Optimal method to marginalize multidimensional distributions
• Let us assume we have a n-dimensional vector and that we know all
the conditional probability expression for the pdf
• We take the following proposal distribution:

17. Gibbs Sampler - 2
• Then:
very efficient
method!

18. Gibbs Sampler – practically

19. Gibbs Sampler – practically
1. §Initialize fix n-1 coordinates and sample
from the resulting pdf
2. for (i=0 ; i < N; i++)
• Sample
• Sample
• Sample
• Sample

20. Gibbs Sampler – example
• Let us pretend we cannot determine the normalization
constant…
… but we can make a comparison with the true marginalized
pdf…

21. Gibbs Sampler – results
• Comparison between Gibbs
Sampling and the true M.-H.
sampling from the marginalized pdf
• Good c2 agreement

22. A complex MCMC application
A radioactive source decays with frequency l1 and a detector records
only every k1 –th event, then at the moment tc the decay rate
changes to l2 and only one event out ofk2 is recorded.
Apparently l1 , k1 , tc , l2 and k2 are undetermined.
We wish to find them.

23. Preparation
• The waiting time for the k-th event in a Poissonian process with
frequency l is distributed according to:
• I can sample a big amount of events from this pdf, changing the
parameters l1 e k1 to l2 e k2 at time tc
• I evaluate the likelihood:

24. Idea
• I assume log-likelihood to be the invariant distribution!
▫ which are the Markov chain states?
struct State {
Parameter
double lambda1, lambda2;
space
double tc;
int k1, k2; Corresponding log-
double plog; likelihood value
State(double la1, double la2, double t, int kk1, int kk2) :
lambda1(la1), lambda2(la2), tc(t), k1(kk1), k2(kk2) {}
State() {};
};

25. Practically
• I have to find an appropriate proposal distribution to move among
the states
▫ Attention: varying li and ki I have toi prevent the acceptance rate to be
too low… but also too high!
• The a ratio is evaluated as the ratio between the final-state and
initial-state likelihood values.
• Try to guess the values for li , ki and tc
• Let the chain evolve for a burn-in time and then record the results.

26. Results • Even if the inital guess is quite far from the real
value, the random walker converges.
guess: l1=5 l2 = 5 k1 = 3 k2 = 2
real: l1=1 l2 = 2 k1 = 1, k2 = 1

27. Results- 2
• Estimate of the uncertainty
l2
l1

28. Results- 3
• All the parameters can be detemined quickly
guess: tc=150 real: tc=300

29. References
• C. Andrieu, N. De Freitas, A. Doucet e M.I. Jordan, Machine Learning 50
(2003), 5-43.
• G. Casella e E.I. George, The American Statistician 46, 3 (1992), 167-174.
• W.H. Press, S. A. Teukolsky, W.T. Vetterling e B.P. Flannery, Numerical
Recipes , Third Edition, Cambridge University Press, 2007.
• M. Loreti, Teoria degli errori e fondamenti di statistica, Decibel, Zanichelli
(1998).
• B. Walsh, Markov Chain Monte Carlo and Gibbs Sampling, Lecture Notes
for EEB 581