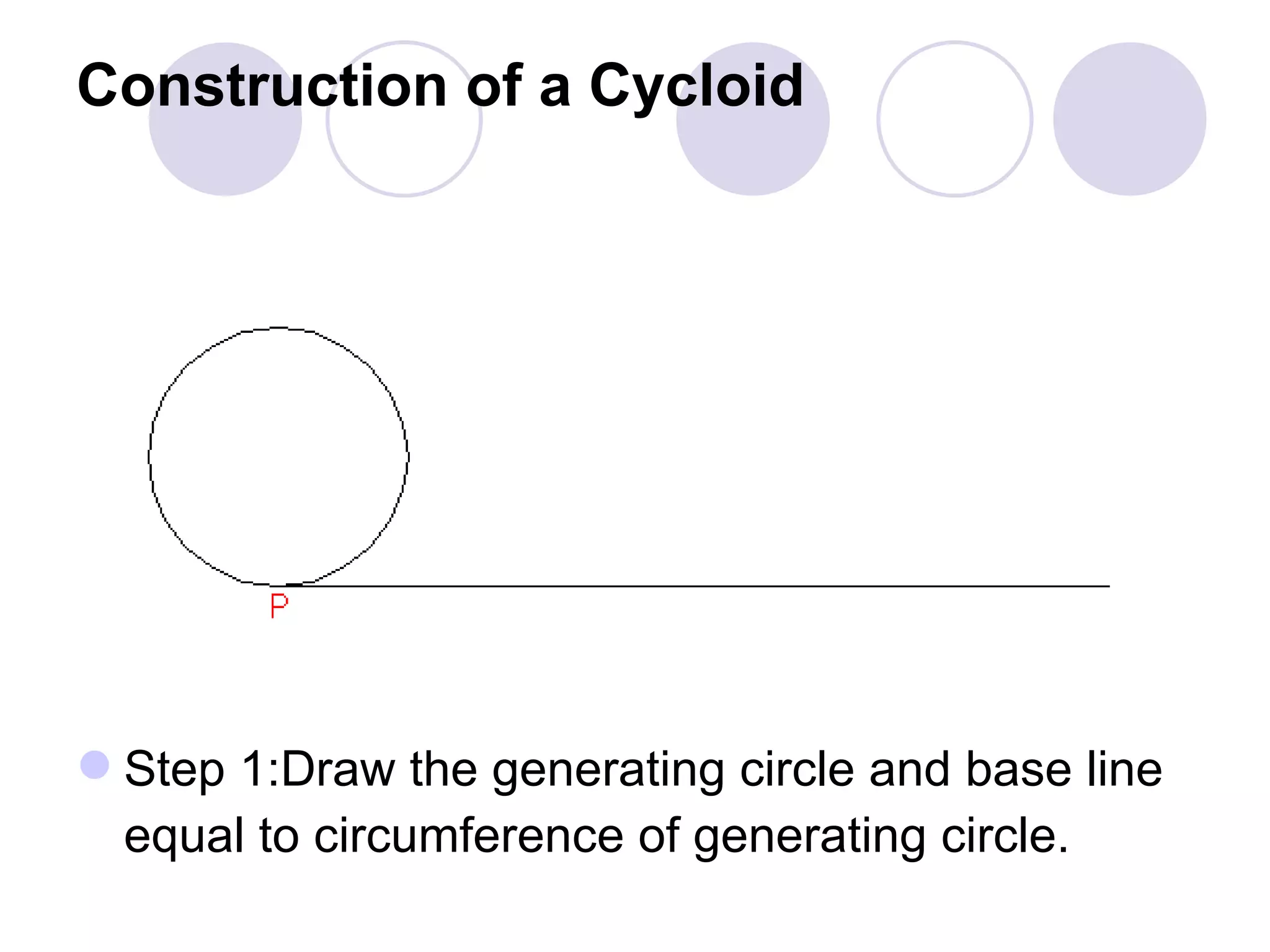
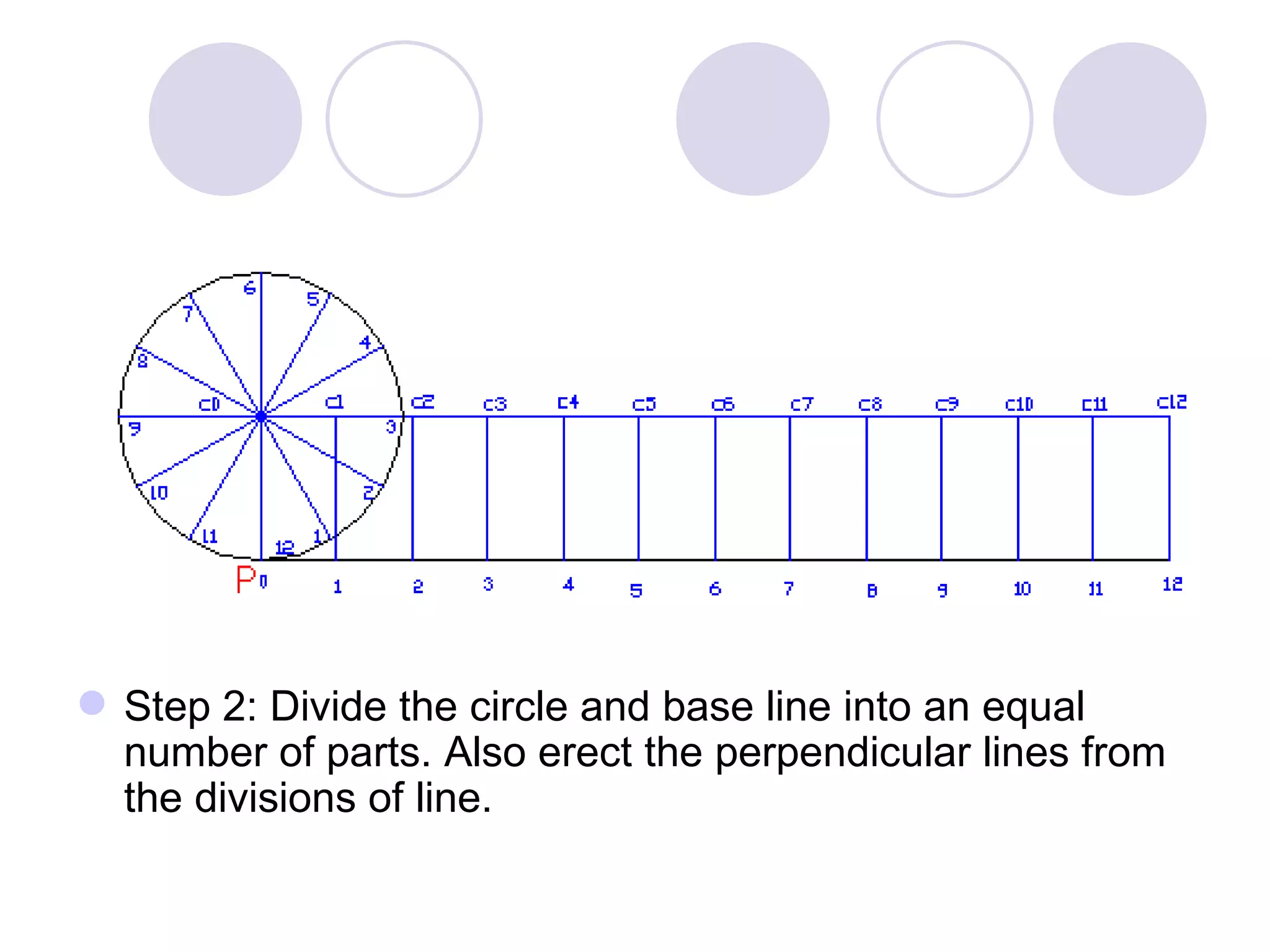
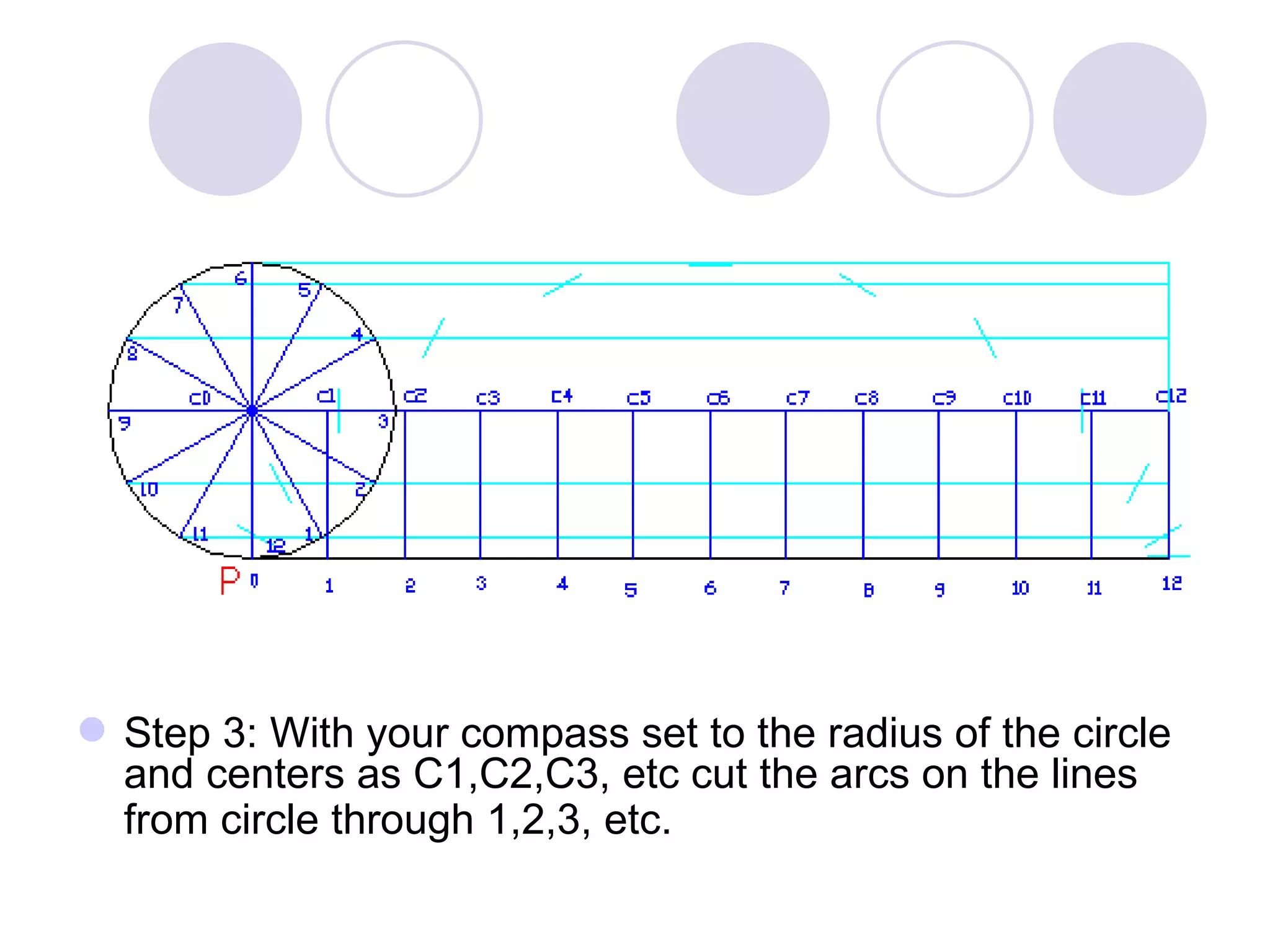
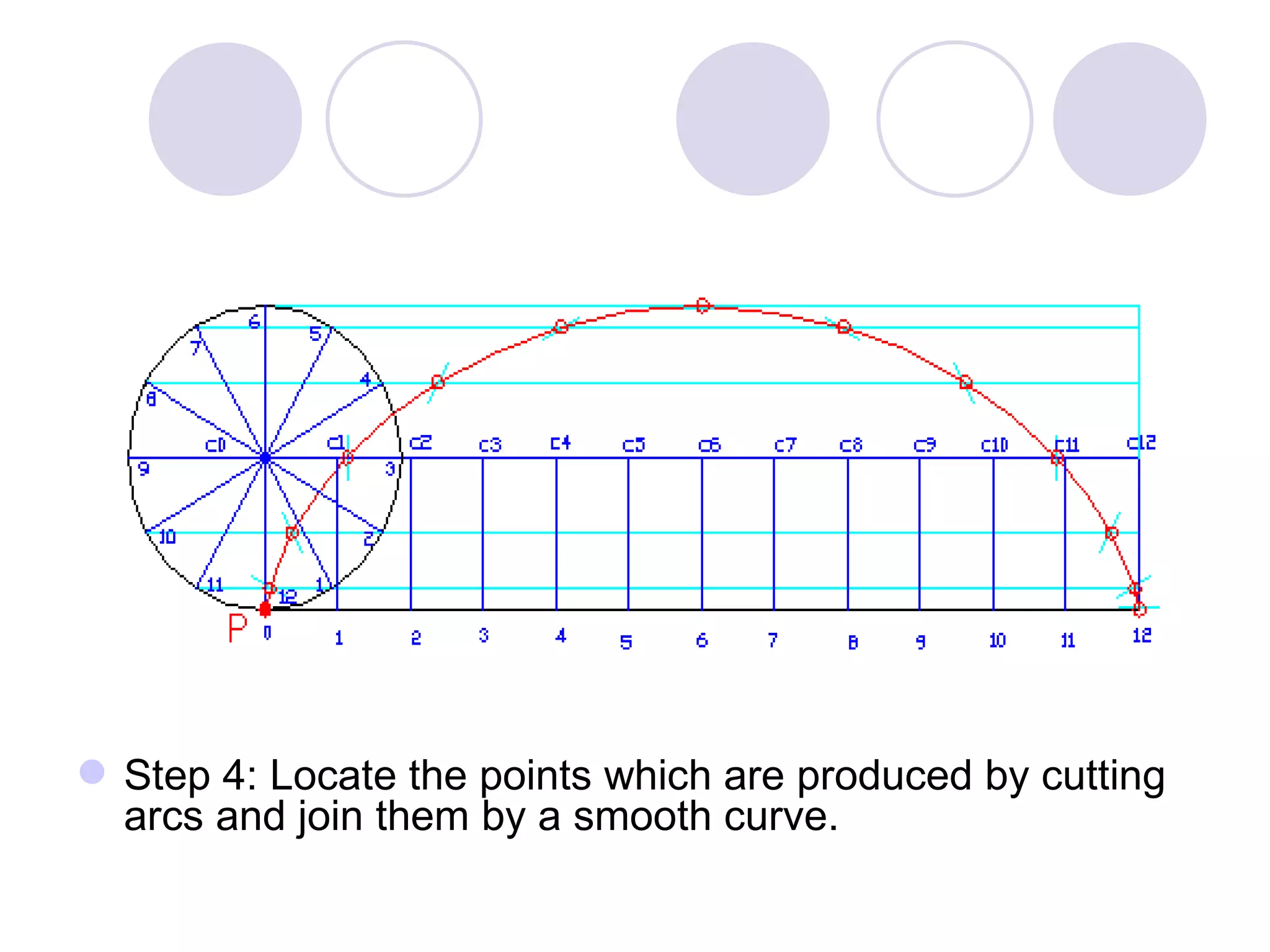
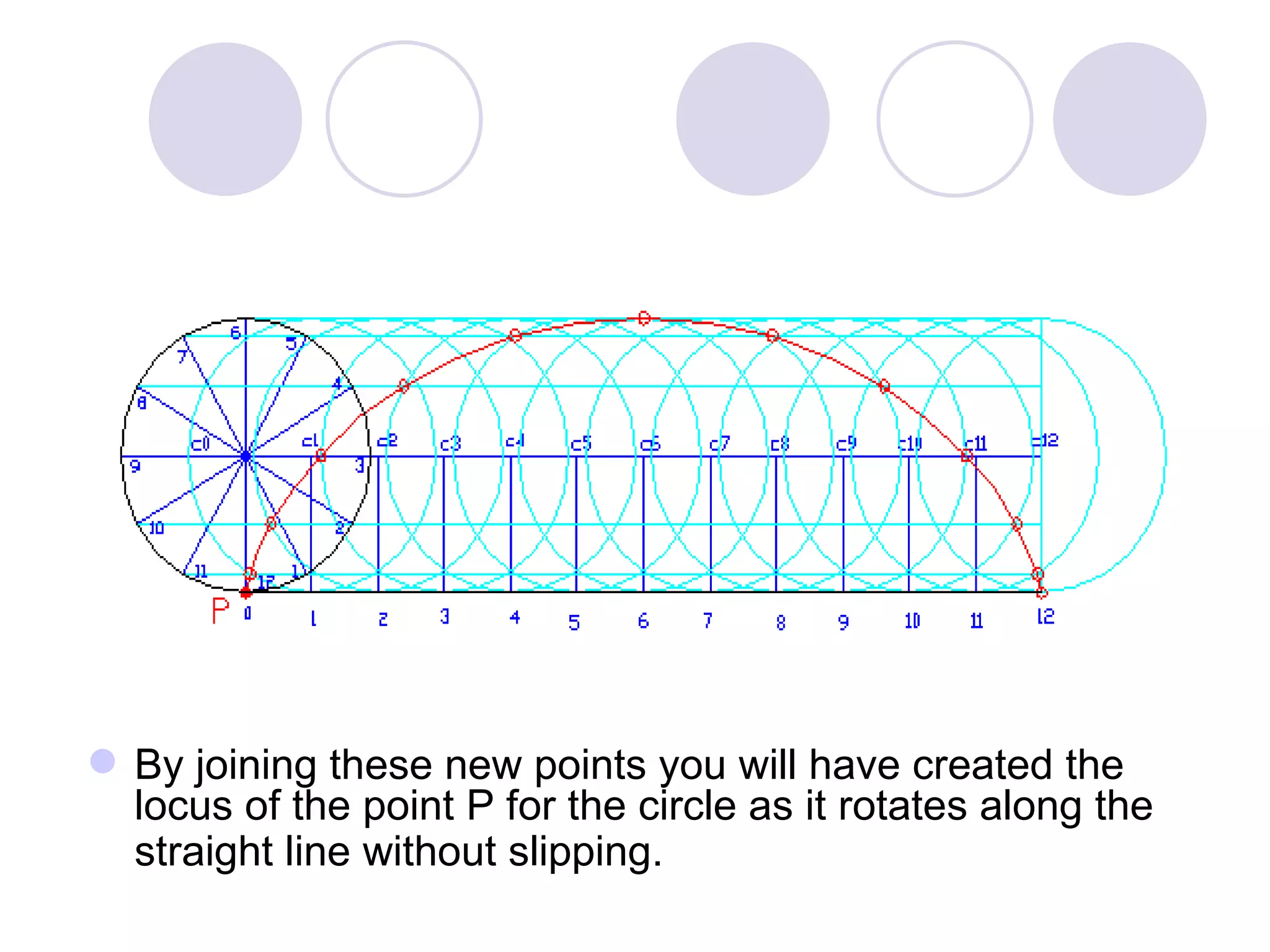
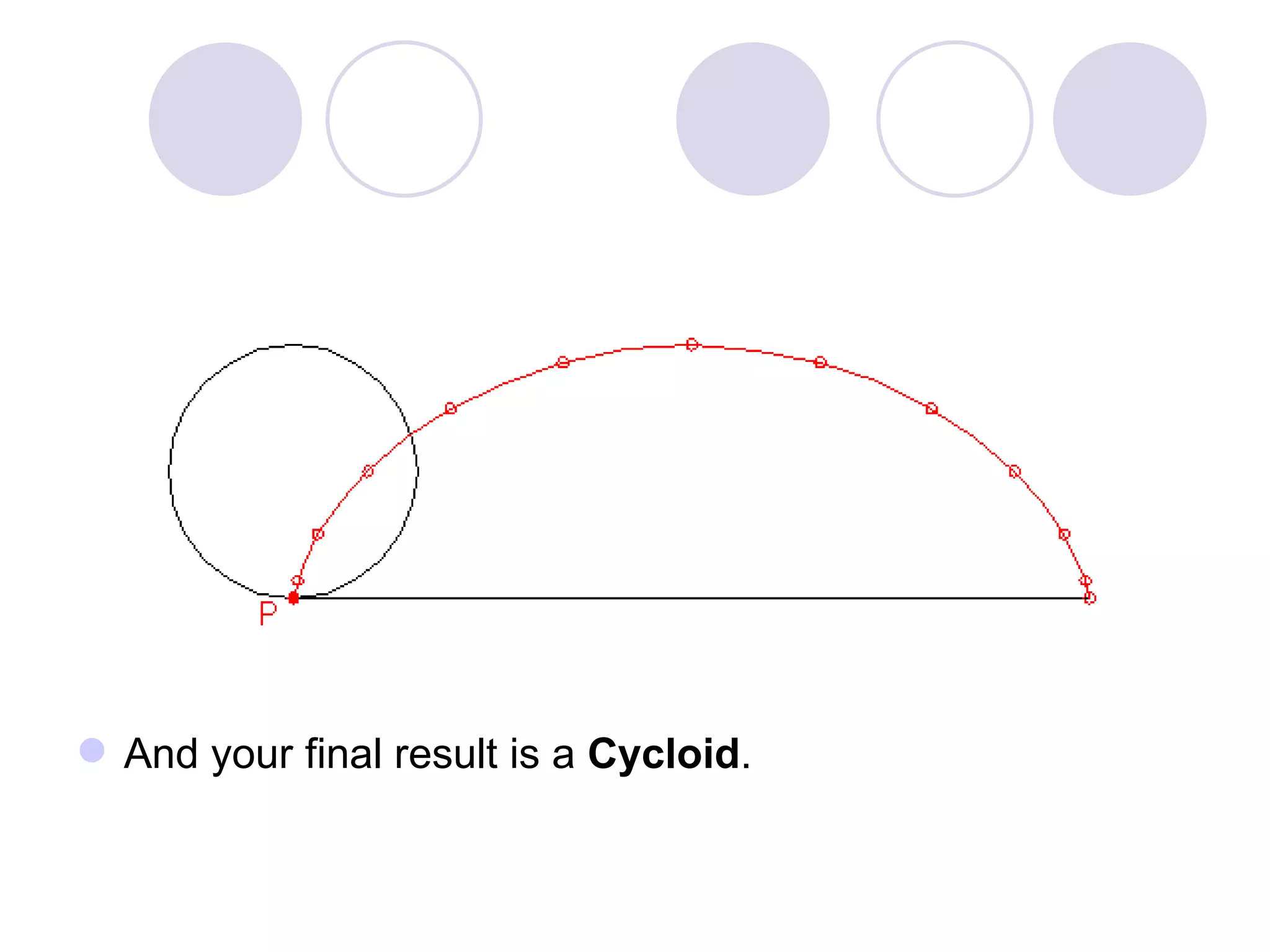
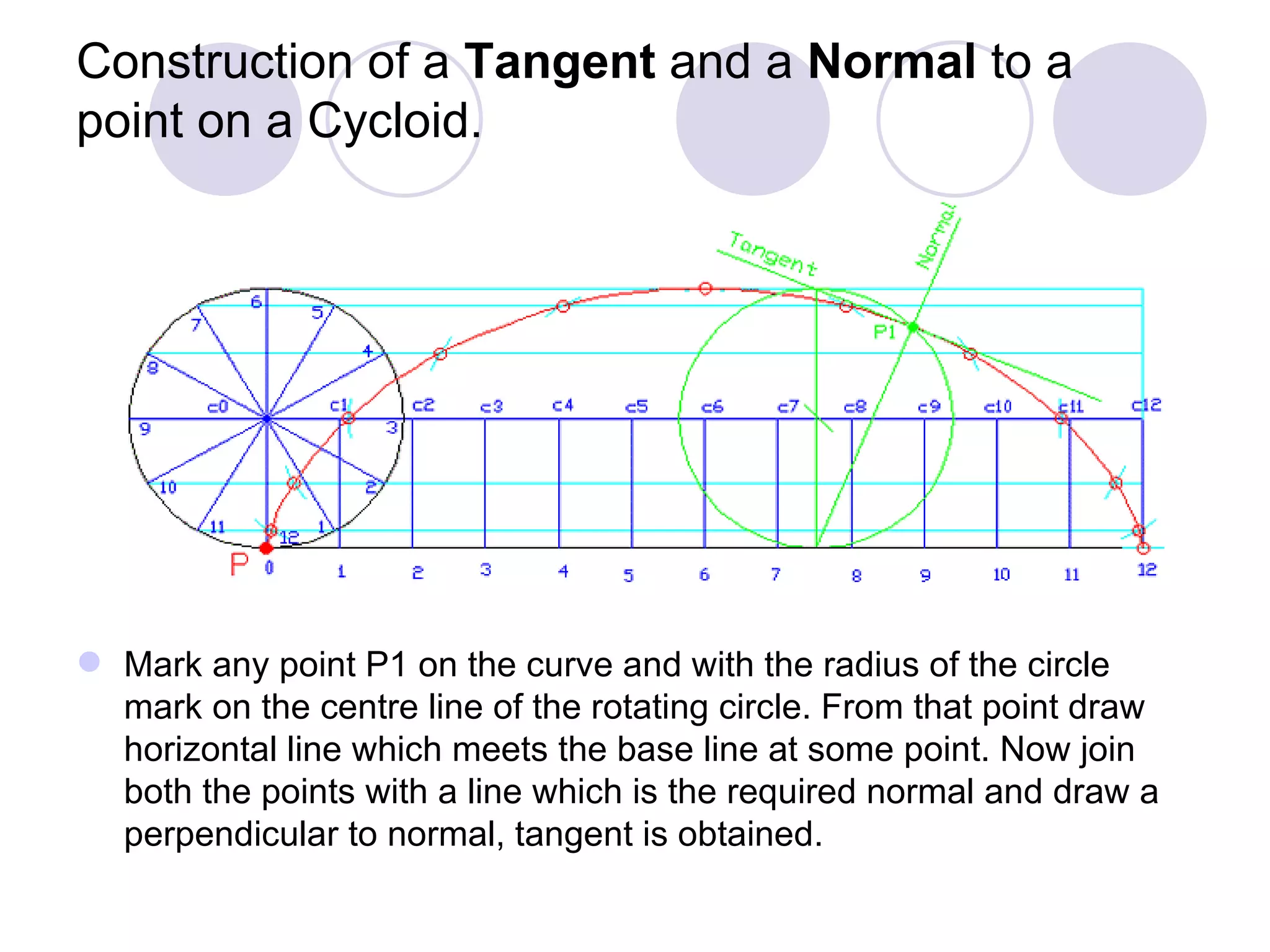
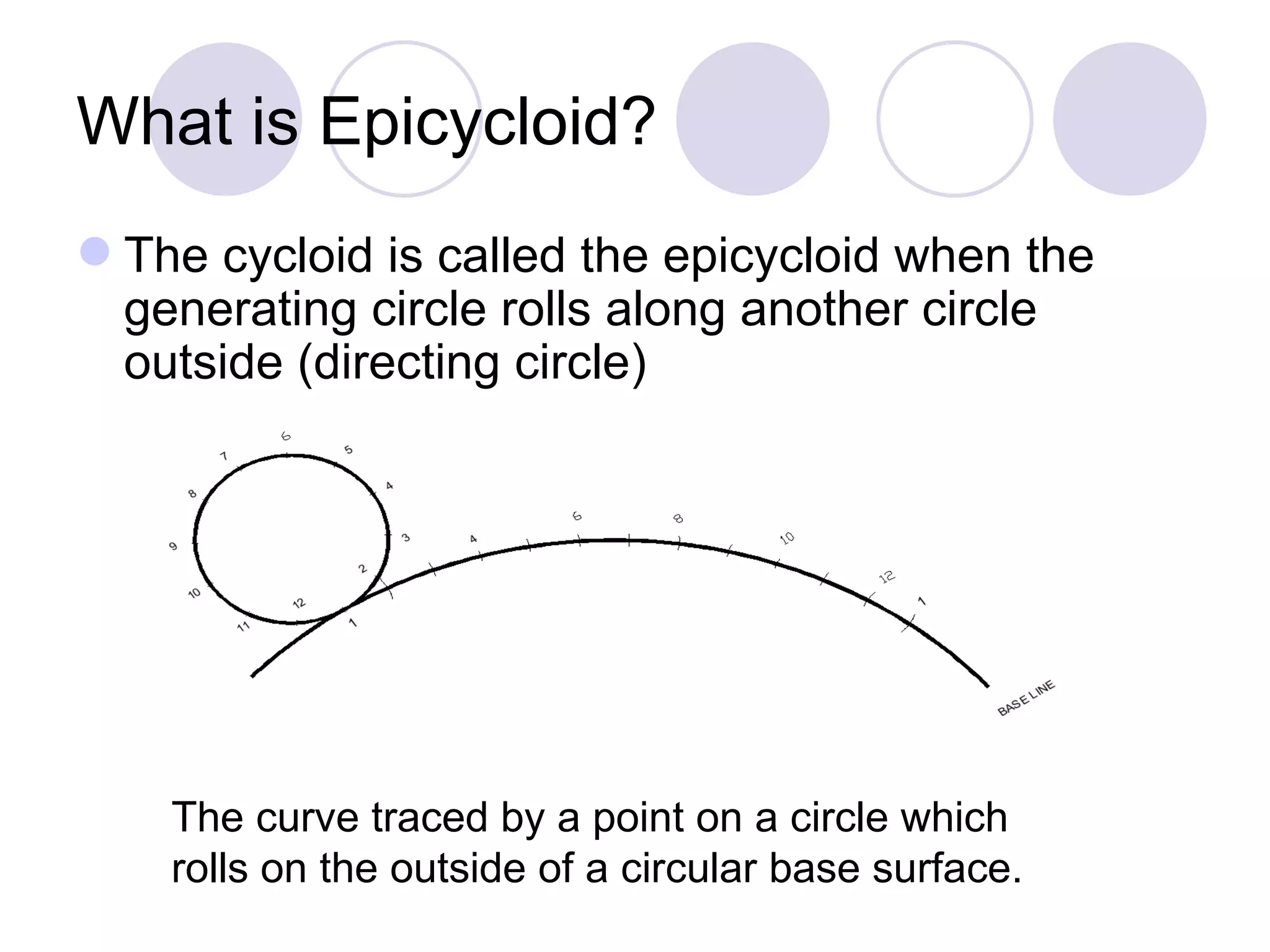
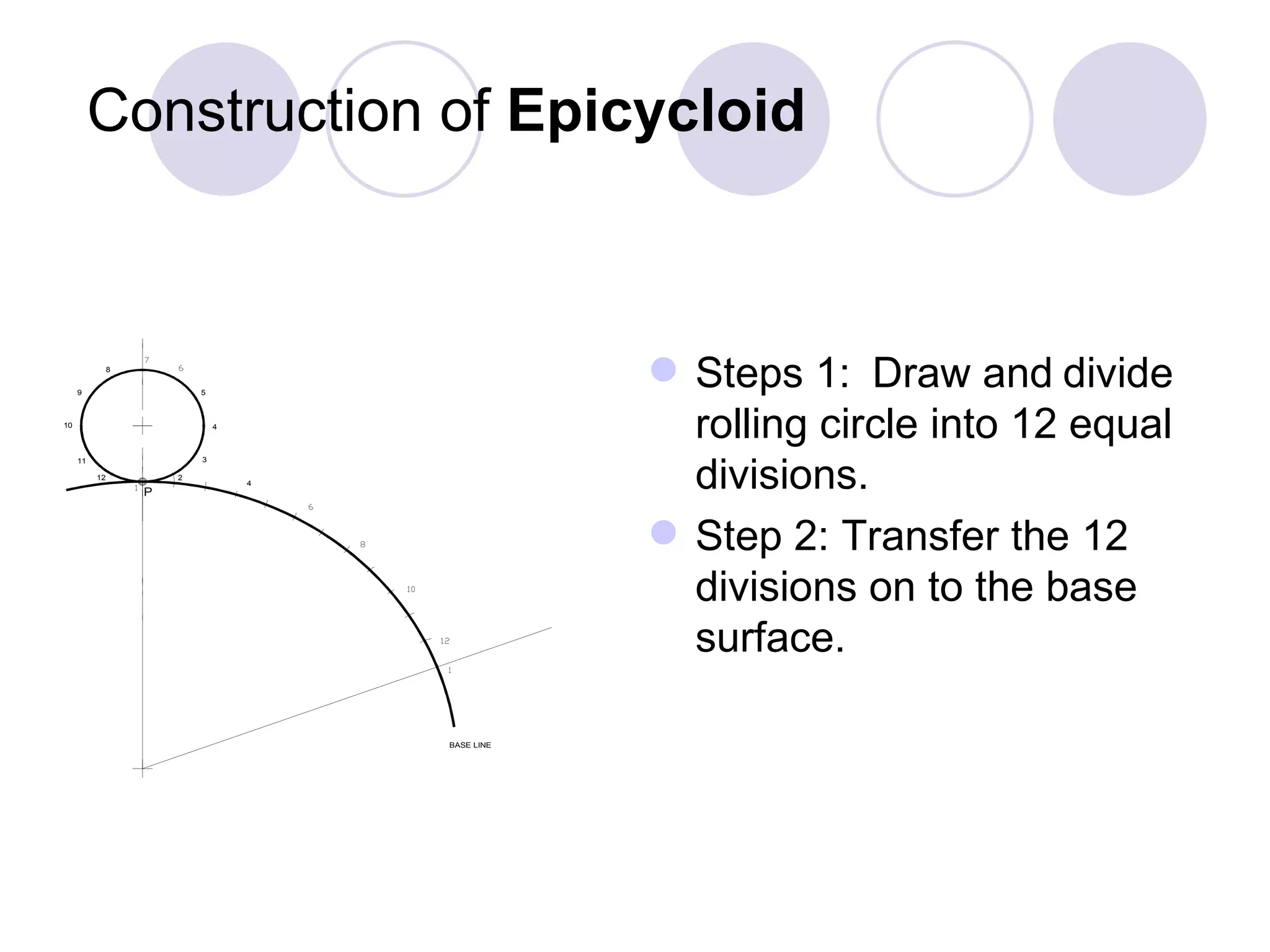
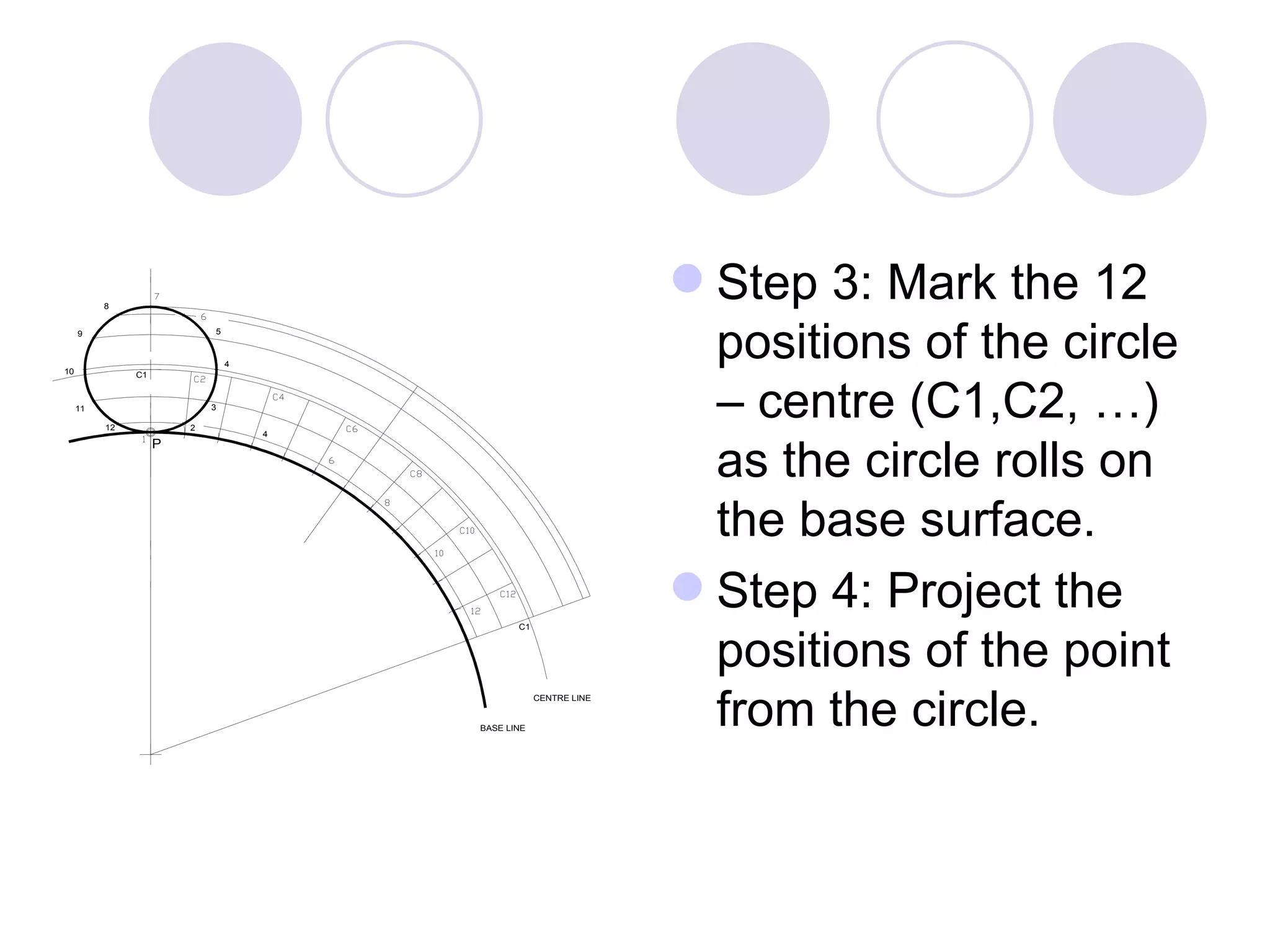
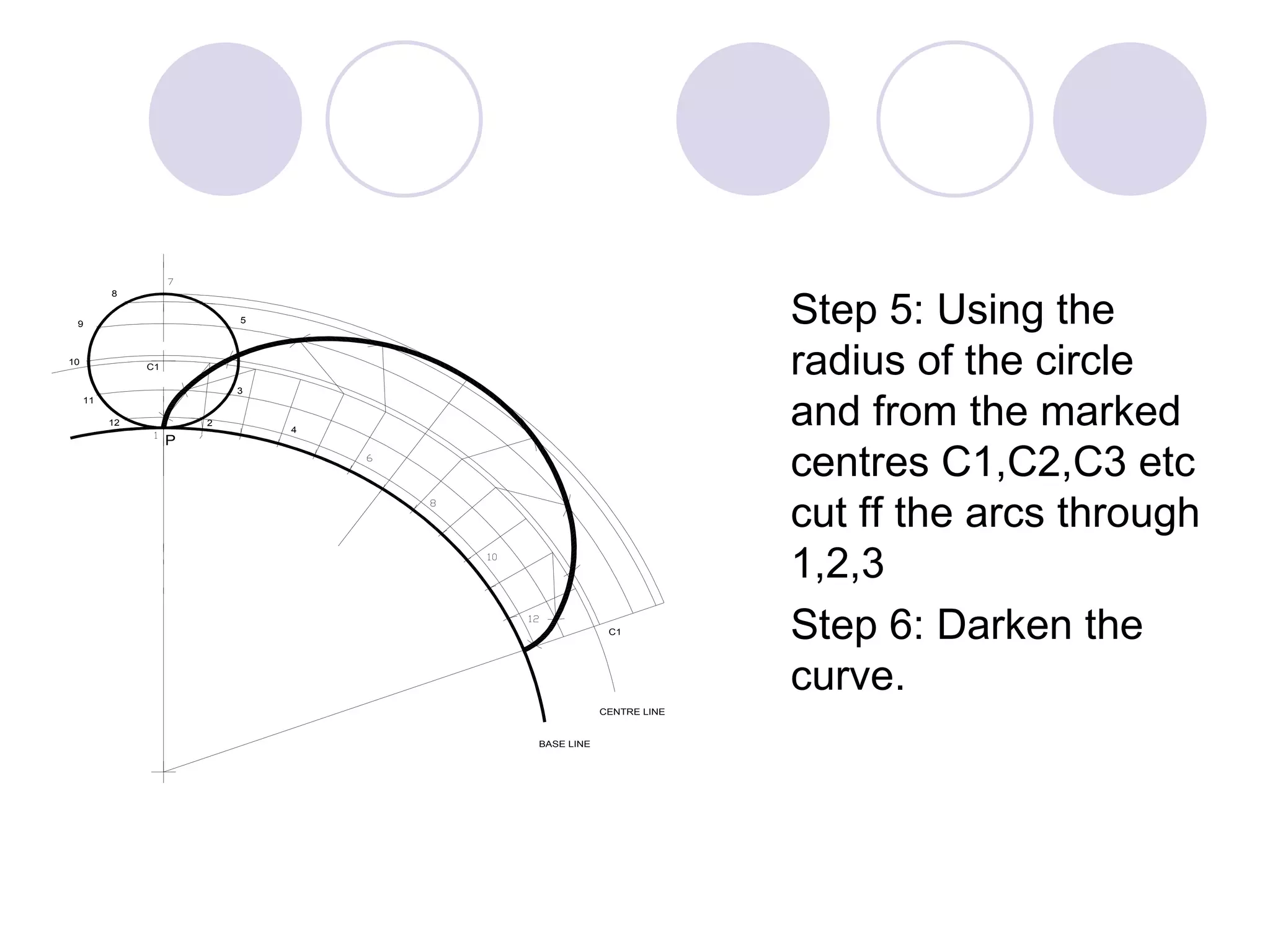
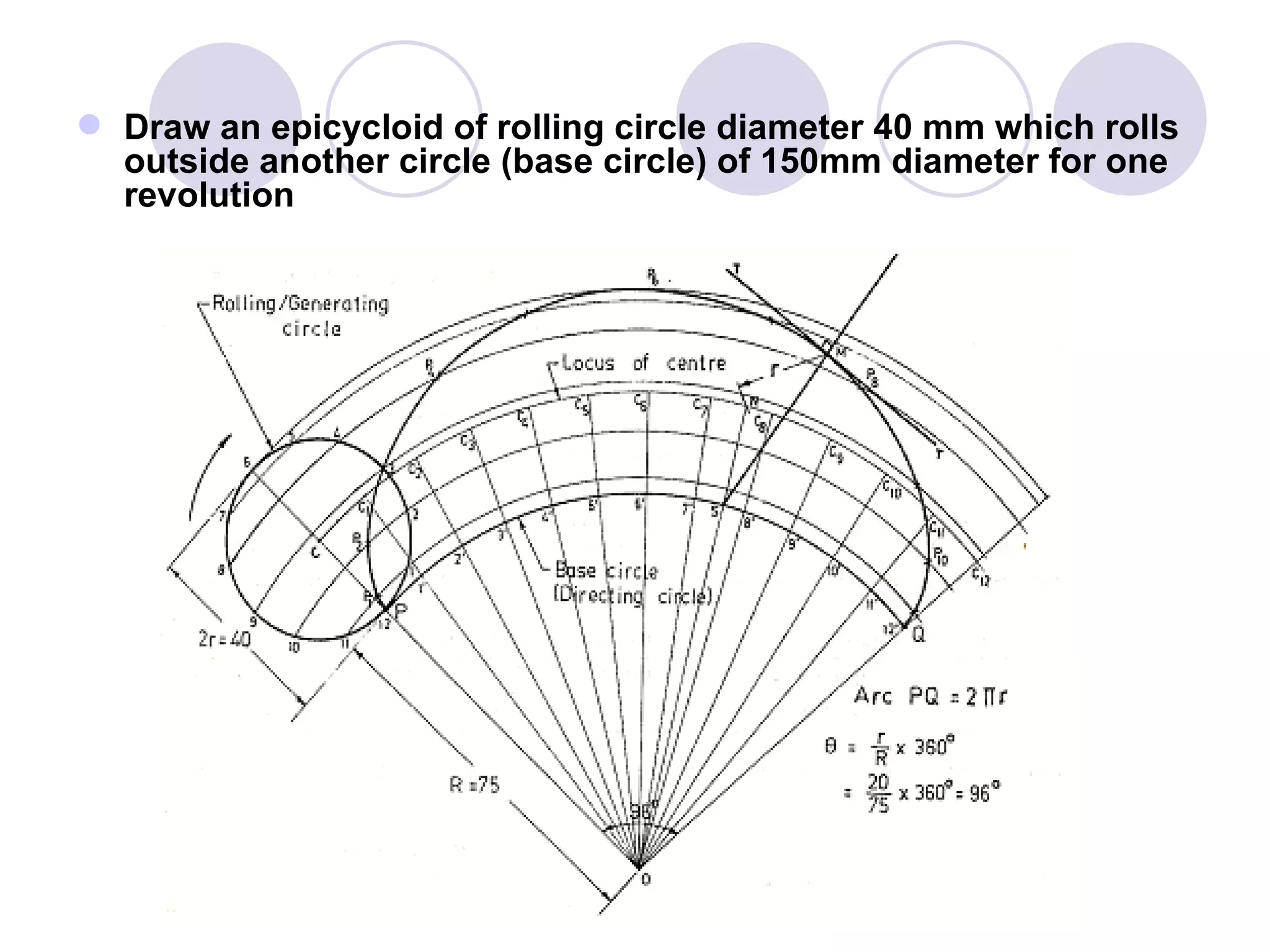
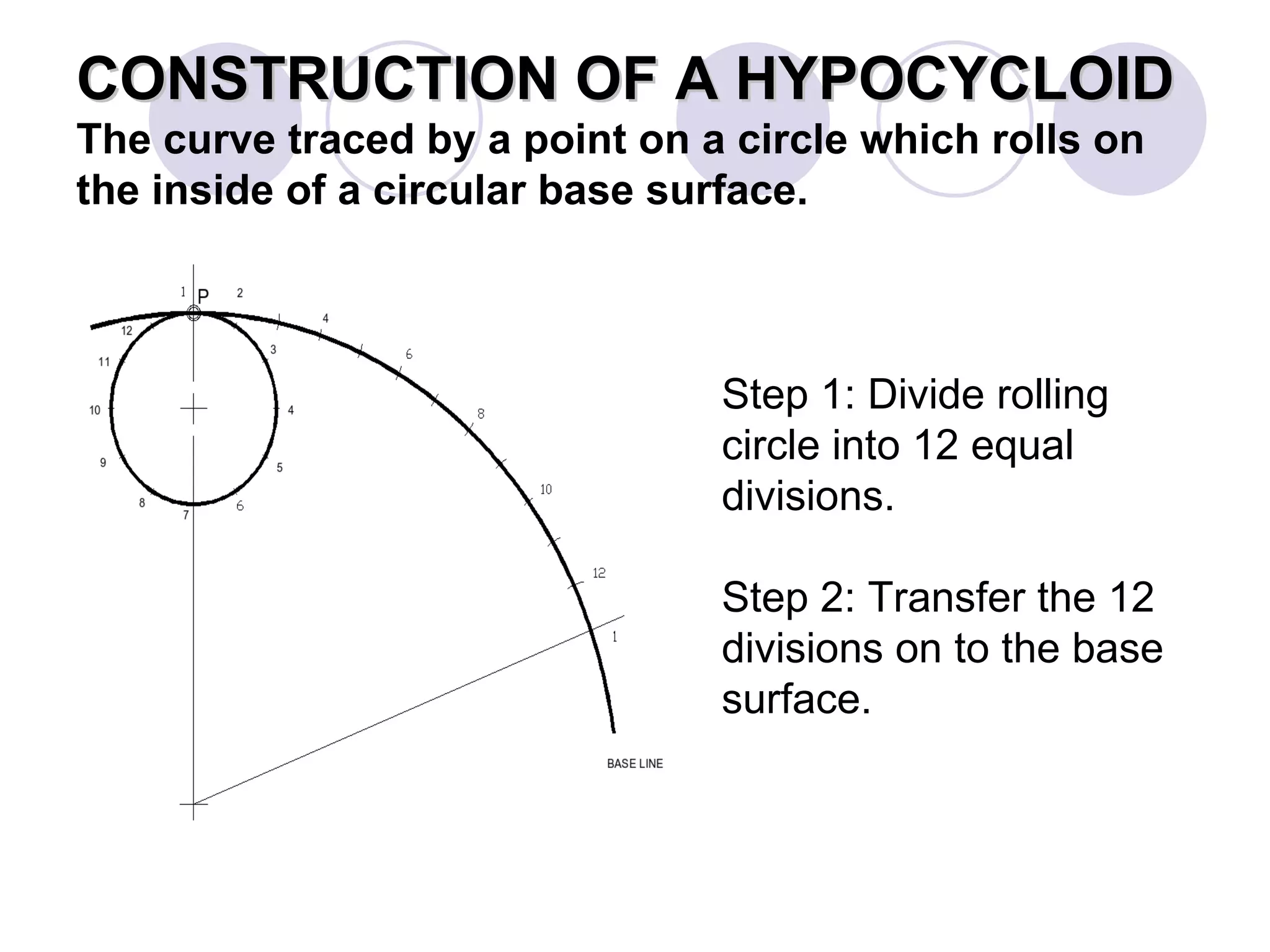
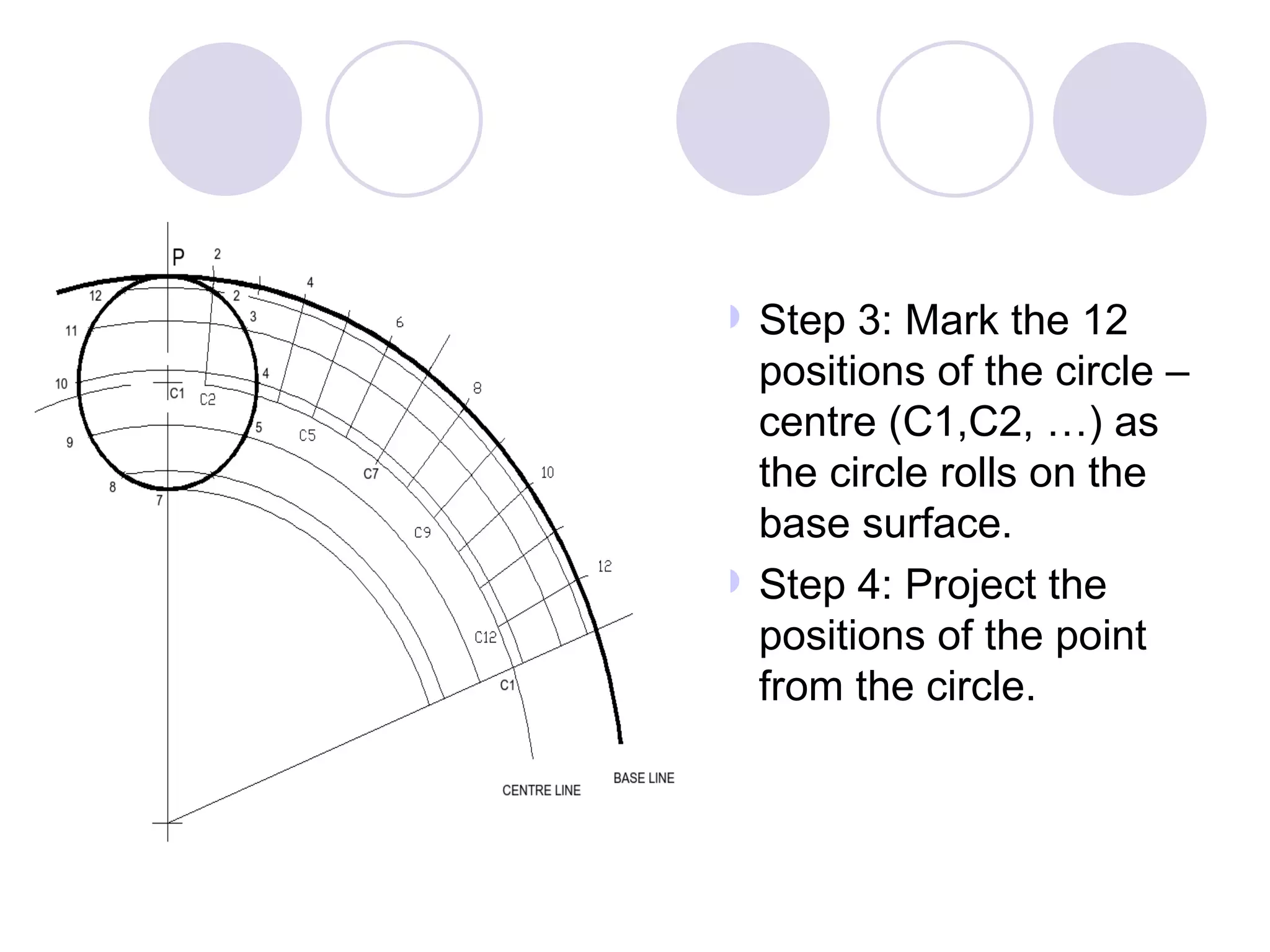
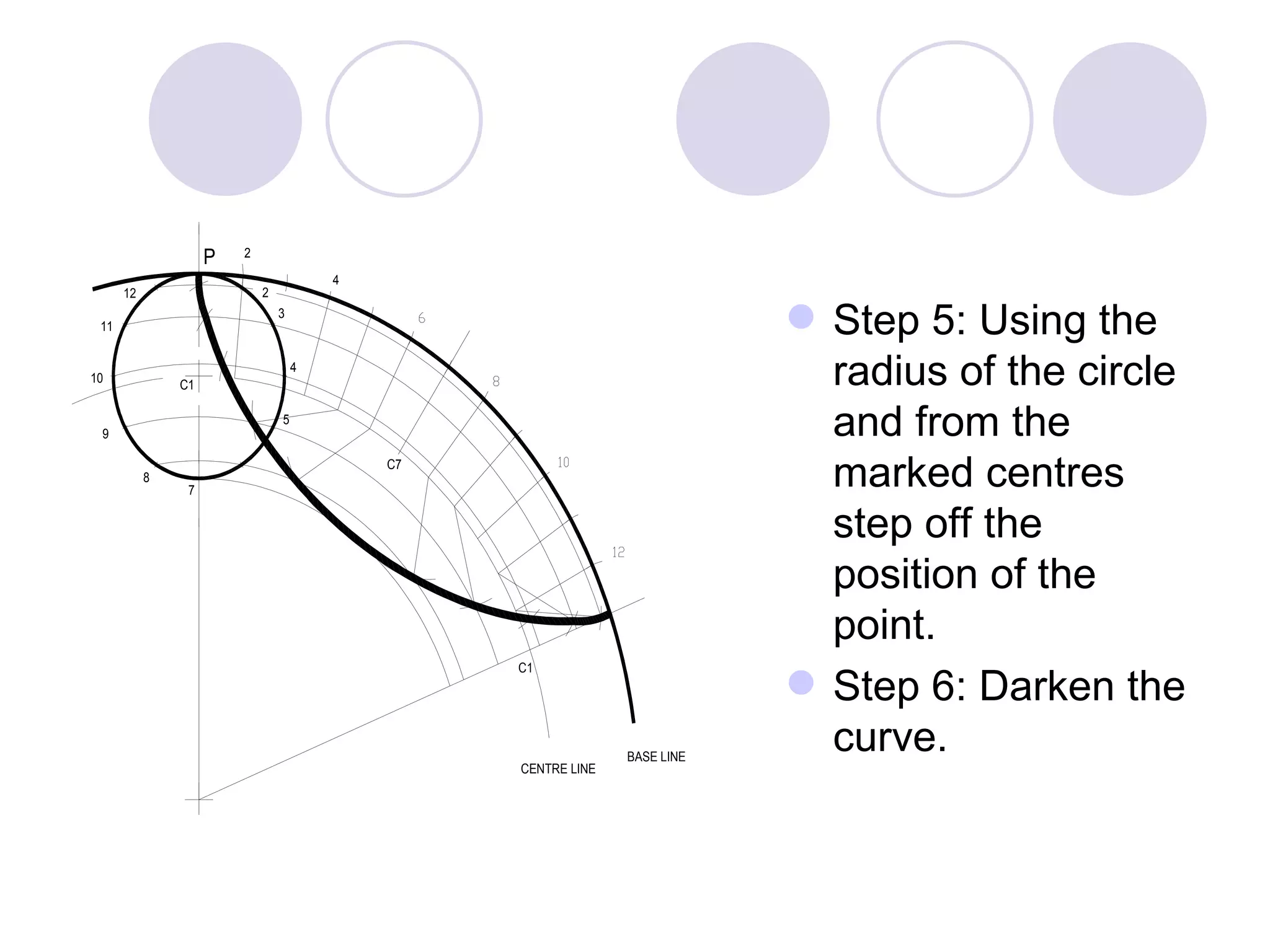
A cycloid is a curve traced by a point on the circumference of a rolling circle. It is generated when a circle rolls along a straight line without slipping. An epicycloid is formed when the generating circle rolls along the outside of another directing circle, while a hypotrochoid is formed when it rolls on the inside. These curves are constructed by marking positions of the generating circle as it rolls and joining the traced points. Cycloids find applications in gear designs, conveyors, and the study of rolling motions in mechanisms.

1. CYCLOIDS

2. What is a Cycloid?
 A cycloid is a curve generated by a point on the
circumference of a circle as the circle rolls along
a straight line without slipping
 The moving circle is called a generating circle
and the straight line is called a directing line or
base line.
 The point on the generating circle which traces
the curve is called the generating point.

3. Construction of a Cycloid
 Step 1:Draw the generating circle and base line
equal to circumference of generating circle.

4.  Step 2: Divide the circle and base line into an equal
number of parts. Also erect the perpendicular lines from
the divisions of line.

5.  Step 3: With your compass set to the radius of the circle
and centers as C1,C2,C3, etc cut the arcs on the lines
from circle through 1,2,3, etc.

6.  Step 4: Locate the points which are produced by cutting
arcs and join them by a smooth curve.

7.  By joining these new points you will have created the
locus of the point P for the circle as it rotates along the
straight line without slipping.

8.  And your final result is a Cycloid.

9. Construction of a Tangent and a Normal to a
point on a Cycloid.
 Mark any point P1 on the curve and with the radius of the circle
mark on the centre line of the rotating circle. From that point draw
horizontal line which meets the base line at some point. Now join
both the points with a line which is the required normal and draw a
perpendicular to normal, tangent is obtained.

10. EPICYCLOIDS

11. What is Epicycloid?
 The cycloid is called the epicycloid when the
generating circle rolls along another circle
outside (directing circle)
The curve traced by a point on a circle which
rolls on the outside of a circular base surface.

12. Construction of Epicycloid
9
8
5
 Steps 1: Draw and divide
10 4
rolling circle into 12 equal
divisions.
11 3
12 2
4
P
 Step 2: Transfer the 12
divisions on to the base
surface.
BASE LINE

13. 8
 Step 3: Mark the 12
10
9
C1
5
4
positions of the circle
11
12 2
3
4
– centre (C1,C2, …)
as the circle rolls on
P
the base surface.
 Step 4: Project the
positions of the point
C1
from the circle.
CENTRE LINE
BASE LINE

14.  Step 5: Using the
8
9 5
10
C1
3
radius of the circle
and from the marked
11
12 2
4
P
centres C1,C2,C3 etc
cut ff the arcs through
1,2,3
C1  Step 6: Darken the
curve.
CENTRE LINE
BASE LINE

15.  Draw an epicycloid of rolling circle diameter 40 mm which rolls
outside another circle (base circle) of 150mm diameter for one
revolution

16.  Step 1: Draw an arc PQ with radius75 mm and centre O,
subtending and angle 96º. P is the generating point. On OP
produced mark PC = 20mm. Draw a circle with centre C and
radius 20 mm.
 Step 2 : Divide rolling diameter in to12 equal parts and name
them as 1,2,3,4… 12 in Clock Wise direction.
 Step 3 : With O as centre draw concentric arcs passing
through1,2,3,…,12.
 Step 4 : With O as centre and OC as radius, draw an arc to
represent locus of centre.
 Step 5 : Divide arc PQ in to 12 equal parts and name them as1’,
2’, …., 12’.
 Step 6 : JoinO1’, O2’, …and produce them to cut the locus of
centers atC1, C2, ….
 Step 7 : Taking C1 as centre, and radius equal to 20 mm, draw
an arc cutting the arc through1 at P1. Similarly obtain pointsP2,
P3,…., P12.

17. HYPOCYCLOIDS

18. CONSTRUCTION OF A HYPOCYCLOID
The curve traced by a point on a circle which rolls on
the inside of a circular base surface.
Step 1: Divide rolling
circle into 12 equal
divisions.
Step 2: Transfer the 12
divisions on to the base
surface.

19.  Step 3: Mark the 12
positions of the circle –
centre (C1,C2, …) as
the circle rolls on the
base surface.
 Step 4: Project the
positions of the point
from the circle.

20. P 2
4
12 2
11
3
 Step 5: Using the
10
C1
4
radius of the circle
9
5
and from the
8
7
C7
marked centres
step off the
position of the
point.
 Step 6: Darken the
C1
BASE LINE
curve.
CENTRE LINE

21.  Applications of cycloid curves:
 Cycloid curves are used in the design of
gear tooth profiles.
 It is also used in the design of conveyor of
mould boxes in foundry shops.

22.  Cycloid
curves are
commonly
used in
kinematics
(motion
studies)
and in
mechanism
s that work
with rolling
contact.