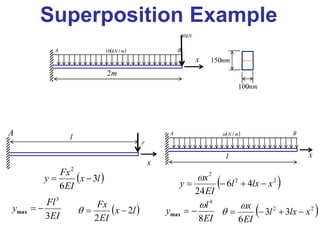
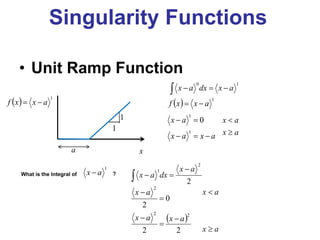
This document discusses using singularity functions to calculate beam deflections. It begins with an example problem of finding the deflection of a simply supported beam with a center load. Singularity functions like the unit step, unit ramp, unit impulse and unit doublet are introduced and used to represent the loading as a function. The loading function is integrated to obtain the shear and moment functions, then integrated again to get the slope and deflection functions. Boundary conditions are applied to determine integration constants, resulting in an equation for the deflection of the beam as a function of position.