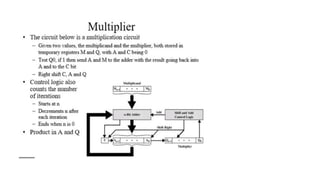
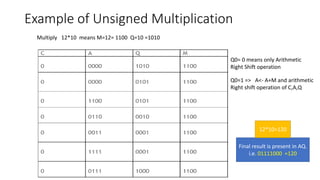
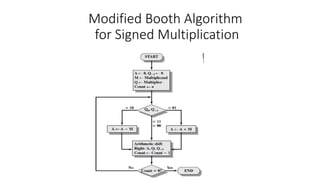
The document outlines the Booth algorithm for multiplication, which simplifies the multiplication process by using repeated addition, analogous to traditional pen-and-paper methods. It differentiates between unsigned and signed multiplication techniques, detailing how the algorithm operates with examples and illustrating the final result in binary format. Additionally, it includes assignments for computing multiplication using both the standard and modified Booth algorithms.

1. Booth Algorithm for Multiplication
Prepared by:- Ms. Snehalata Agasti
CSE Department

2. Shift-And-Add multiplication
• Operation is similar to multiplication using pen and paper.
• This method adds the multiplicand X to itself Y times , where Y is multiplier.
• Let multiply X=8= 1000 and Y= 9 =1001
1000
x 1001
1 0 0 0
0 0 0 0
0 0 0 0
1 0 0 0
1001000
• If n-number of bits are present in multiplier and multiplicand then 2n number of bits
required to store the result.
• Multiplication is complex operation. It can be replaced by repeated addition.
Partial product
Final Result

4. Booth Multiplication Algorithm
for Unsigned Number
Count = n means number of
bits present in multiplier(Q).

5. Example of Unsigned Multiplication
Q0= 0 means only Arithmetic
Right Shift operation
Q0=1 => A<- A+M and arithmetic
Right shift operation of C,A,Q
Final result is present in AQ.
i.e. 01111000 =120
Multiply 12*10 means M=12= 1100 Q=10 =1010
12*10=120

6. Modified Booth Algorithm
for Signed Multiplication

7. Example of Multiplication using Booth
Algorithm
Q0Q -1 == 00 or 11 only Right shift
operation of AQQ -1
Q0Q -1 == 01 , A  A+M
Then Right shift operation of AQQ -1
Q0Q -1 == 10 , A  A - M
Then Right shift operation of AQQ -1
Final result is present in AQ.
i.e. (00010101)2 = (21)10
7*3 =21

8. Assignment
• Compute 15*10 using Booth’s unsigned multiplication technique.
• Compute 15*10 using modified Booth algorithm.