Download to read offline
Uploaded byCSIRO
Algorithm evaluation using Item Response Theory
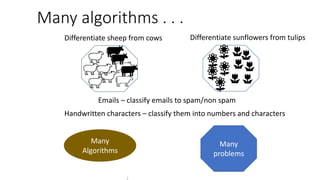
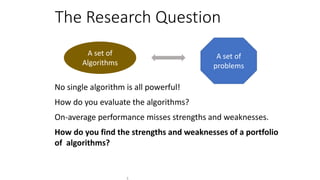
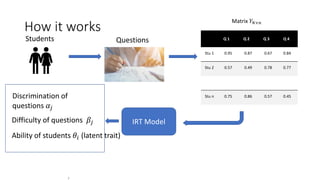
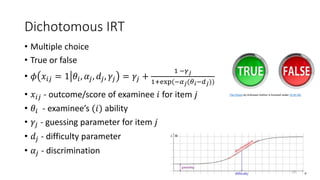
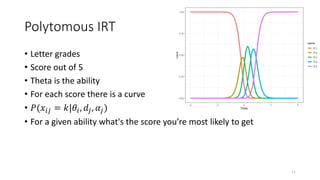
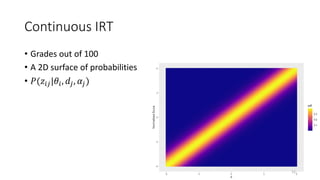
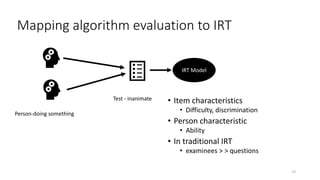
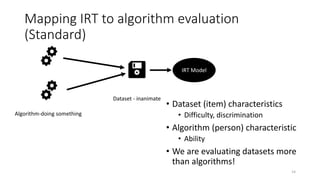
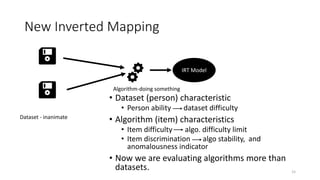
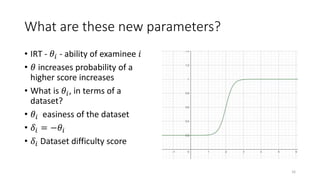
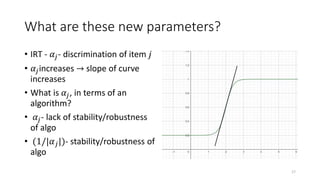
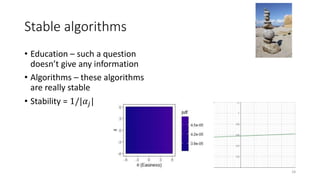
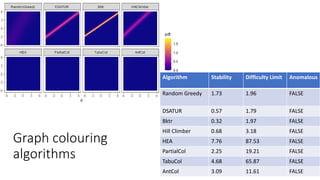
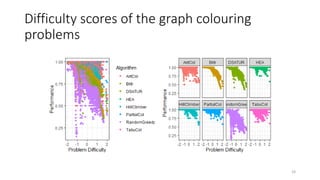
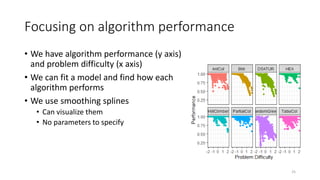
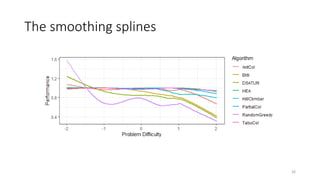
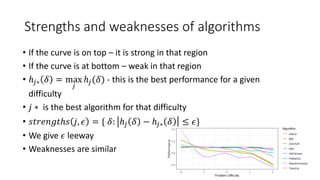
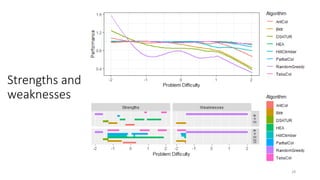
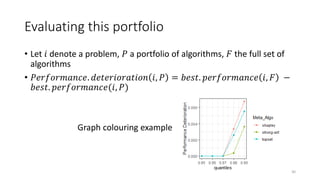
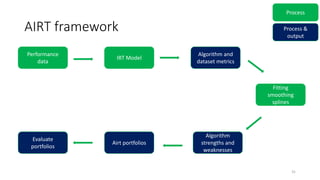
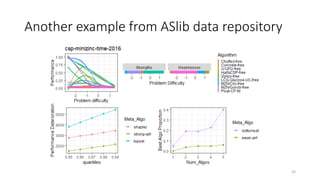
The document discusses the evaluation of algorithm portfolios using Item Response Theory (IRT), highlighting its application in assessing algorithm strengths and weaknesses within various problem domains. IRT is adapted from psychometrics to analyze classifier performance, focusing on the hidden abilities of datasets and the effectiveness of algorithms. The research introduces new metrics and methods for evaluating algorithm portfolios, leading to the development of the AIRT framework for selecting strong and weak algorithm combinations.
More Related Content
Similar to Algorithm evaluation using Item Response Theory
Algorithm evaluation using Item Response Theory
- 1. Evaluating algorithm portfolios using Item Response Theory •Sevvandi Kandanaarachchi RMIT University • OPTIMA Seminar Series • May 4th 2022 • Joint work with Prof Kate Smith-Miles 1 This Photo by Unknown Author is licensed under CC BY-ND
- 2. Many algorithms .. . 2 Many problems Differentiate sheep from cows Many problems Differentiate sunflowers from tulips Emails – classify emails to spam/non spam Handwritten characters – classify them into numbers and characters Many Algorithms
- 3. The Research Question 3 Aset of problems A set of Algorithms No single algorithm is all powerful! How do you evaluate the algorithms? On-average performance misses strengths and weaknesses. How do you find the strengths and weaknesses of a portfolio of algorithms?
- 4. Overview Introduction to Item Response Theory(IRT) Mapping IRT to algorithm evaluation New metrics and reinterpretation Strengths and weaknesses Examples
- 5. Item Response Theory (IRT) •Latent trait models used in social sciences/psychometrics • Unobservable characteristics and observed outcomes • Verbal or mathematical ability • Racial prejudice or stress proneness • Political inclinations • Intrinsic “quality” that cannot be measured directly This Photo by Unknown Author is licensed under CC BY-SA
- 6. IRT in education •Finds the discrimination and difficulty of test questions • And the ability of the test participants • By fitting an IRT model • In education – questions that can discriminate between students with different ability is preferred to “very difficult” questions. 6
- 7. How it works 7 Questions StudentsQ 1 Q 2 Q 3 Q 4 Stu 1 0.95 0.87 0.67 0.84 Stu 2 0.57 0.49 0.78 0.77 Stu n 0.75 0.86 0.57 0.45 IRT Model Discrimination of questions 𝛼𝑗 Difficulty of questions 𝛽𝑗 Ability of students 𝜃𝑖 (latent trait) Matrix 𝑌𝑁×𝑛
- 8. IRT in psychometrics •A survey • Rosenberg's Self-Esteem Scale • I feel I am a person of worth (Strongly Agree/Agree/Neutral/... ) • Use original responses (no marking as in education) • Fit the IRT model • Output • Participants self-esteem (hidden quality = latent trait) • Question discrimination • Question difficulty • Focus is on the hidden ability 8
- 9. IRT in DataScience/Machine Learning • Relatively new area of research • From performance data find • Ability of classifiers • Discrimination/difficulty of datasets • 2019 - Item response theory in AI: Analysing machine learning classifiers at the instance level – F. Martínez-Plumed et al. 9
- 10. Dichotomous IRT • Multiplechoice • True or false • 𝜙 𝑥𝑖𝑗 = 1 𝜃𝑖, 𝛼𝑗, 𝑑𝑗, 𝛾𝑗 = 𝛾𝑗 + 1 −𝛾𝑗 1+exp(−𝛼𝑗(𝜃𝑖−𝑑𝑗)) • 𝑥𝑖𝑗 - outcome/score of examinee 𝑖 for item 𝑗 • 𝜃𝑖 - examinee’s (𝑖) ability • 𝛾𝑗 - guessing parameter for item 𝑗 • 𝑑𝑗 - difficulty parameter • 𝛼𝑗 - discrimination This Photo by Unknown Author is licensed under CC BY-NC 10
- 11. Polytomous IRT • Lettergrades • Score out of 5 • Theta is the ability • For each score there is a curve • 𝑃(𝑥𝑖𝑗 = 𝑘|𝜃𝑖, 𝑑𝑗, 𝛼𝑗) • For a given ability what's the score you’re most likely to get 11
- 12. Continuous IRT • Gradesout of 100 • A 2D surface of probabilities • 𝑃(𝑧𝑖𝑗|𝜃𝑖, 𝑑𝑗, 𝛼𝑗) 12
- 13. Mapping algorithm evaluationto IRT • Item characteristics • Difficulty, discrimination • Person characteristic • Ability • In traditional IRT • examinees > > questions IRT Model Person-doing something Test - inanimate 13
- 14. Mapping IRT toalgorithm evaluation (Standard) • Dataset (item) characteristics • Difficulty, discrimination • Algorithm (person) characteristic • Ability • We are evaluating datasets more than algorithms! IRT Model Algorithm-doing something Dataset - inanimate 14
- 15. New Inverted Mapping •Dataset (person) characteristic • Person ability dataset difficulty • Algorithm (item) characteristics • Item difficulty algo. difficulty limit • Item discrimination algo stability, and anomalousness indicator • Now we are evaluating algorithms more than datasets. IRT Model Algorithm-doing something Dataset - inanimate 15
- 16. What are thesenew parameters? • IRT - 𝜃𝑖 - ability of examinee 𝑖 • 𝜃 increases probability of a higher score increases • What is 𝜃𝑖, in terms of a dataset? • 𝜃𝑖 easiness of the dataset • 𝛿𝑖 = −𝜃𝑖 • 𝛿𝑖 Dataset difficulty score 16
- 17. What are thesenew parameters? • IRT - 𝛼𝑗- discrimination of item 𝑗 • 𝛼𝑗increases → slope of curve increases • What is 𝛼𝑗, in terms of an algorithm? • 𝛼𝑗- lack of stability/robustness of algo • (1/|𝛼𝑗|)- stability/robustness of algo 17
- 18. Stable algorithms • Education– such a question doesn’t give any information • Algorithms – these algorithms are really stable • Stability = 1/|𝛼𝑗| 18
- 19. Anomalous algorithms • Algorithmsthat perform poorly on easy datasets and well on difficult datasets • Negative discrimination • In education – such items are discarded or revised • If an algorithm anomalous, it is interesting • Anomalousness = sign(𝛼𝑗) This Photo by Unknown Author is licensed under CC BY-NC-ND 19
- 20. Fitting the IRTmodel • Maximising the expectation • 𝐸 = 𝑁 𝑗(ln 𝛼𝑗 + ln |𝛾𝑗|) − 1/ 2 𝑖 𝑗 𝛼𝑗 2 𝛽𝑗 + 𝛾𝑗𝑧𝑖𝑗 − 𝜇𝑖 𝑡 2 +
- 21. After fitting themodel, we get . . . • Algorithm metrics • Stability, difficulty limit, anomalousness indicator • Dataset metrics • Difficulty scores 21
- 22. Example – fittingIRT model • Graph Colouring algorithms (Smith-Miles et al 2014) • 8 graph colouring algorithms • RandomGreedy, DSATUR, Bktr, HillClimber, HEA, PartialCol, TabuCol, AntCol • How many colours did each algorithm use to colour 6712 graphs 22
- 23. Graph colouring algorithms 23 Algorithm StabilityDifficulty Limit Anomalous Random Greedy 1.73 1.96 FALSE DSATUR 0.57 1.79 FALSE Bktr 0.32 1.97 FALSE Hill Climber 0.68 3.18 FALSE HEA 7.76 87.53 FALSE PartialCol 2.25 19.21 FALSE TabuCol 4.68 65.87 FALSE AntCol 3.09 11.61 FALSE
- 24. Difficulty scores ofthe graph colouring problems 24
- 25. Focusing on algorithmperformance • We have algorithm performance (y axis) and problem difficulty (x axis) • We can fit a model and find how each algorithm performs • We use smoothing splines • Can visualize them • No parameters to specify 25
- 26.
- 27. Strengths and weaknessesof algorithms • If the curve is on top – it is strong in that region • If the curve is at bottom – weak in that region • ℎ𝑗∗ 𝛿 = max 𝑗 ℎ𝑗(𝛿) - this is the best performance for a given difficulty • 𝑗 ∗ is the best algorithm for that difficulty • 𝑠𝑡𝑟𝑒𝑛𝑔𝑡ℎ𝑠 𝑗, 𝜖 = { 𝛿: ℎ𝑗 𝛿 − ℎ𝑗∗ 𝛿 ≤ 𝜖} • We give 𝜖 leeway • Weaknesses are similar 27
- 28.
- 29. Algorithm portfolio selection •Can use algorithm strengths to select a good portfolio of algorithms • We call this portfolio airt portfolio • airt – Algorithm IRT (old Scottish word – to guide) • 𝑆𝑡𝑟𝑜𝑛𝑔 𝑎𝑖𝑟𝑡 𝑝𝑜𝑟𝑡𝑓𝑜𝑙𝑖𝑜 𝜖 = 𝑠𝑒𝑡 𝑜𝑓 𝑎𝑙𝑔𝑜𝑟𝑖𝑡ℎ𝑚𝑠 𝑤𝑖𝑡ℎ 𝑠𝑡𝑟𝑒𝑛𝑔𝑡ℎ𝑠 (𝜖) • Similarly, we can select a weak portfolio as well • 𝑊𝑒𝑎𝑘 𝑎𝑖𝑟𝑡 𝑝𝑜𝑟𝑡𝑓𝑜𝑙𝑖𝑜 𝜖 = 𝑠𝑒𝑡 𝑜𝑓 𝑎𝑙𝑔𝑜𝑟𝑖𝑡ℎ𝑚𝑠 𝑤𝑖𝑡ℎ 𝑤𝑒𝑎𝑘𝑛𝑒𝑠𝑠𝑒𝑠 𝜖 29
- 30. Evaluating this portfolio •Let 𝑖 denote a problem, 𝑃 a portfolio of algorithms, 𝐹 the full set of algorithms • 𝑃𝑒𝑟𝑓𝑜𝑟𝑚𝑎𝑛𝑐𝑒. 𝑑𝑒𝑡𝑒𝑟𝑖𝑜𝑟𝑎𝑡𝑖𝑜𝑛 𝑖, 𝑃 = 𝑏𝑒𝑠𝑡. 𝑝𝑒𝑟𝑓𝑜𝑟𝑚𝑎𝑛𝑐𝑒 𝑖, 𝐹 − 𝑏𝑒𝑠𝑡. 𝑝𝑒𝑟𝑓𝑜𝑟𝑚𝑎𝑛𝑐𝑒(𝑖, 𝑃) Graph colouring example 30
- 31. AIRT framework 31 Performance data IRT Model Algorithmand dataset metrics Fitting smoothing splines Algorithm strengths and weaknesses Airt portfolios Evaluate portfolios Process Process & output
- 32. Another example fromASlib data repository 32
- 33. • SAT11-individual example • Examplewhere airt doesn’t do so well. • The curves are quite similar to each other • Reason to believe SAT11 has pre-selected algorithms 33
- 34. AIRT performs well,when . . . • The set of algorithms is diverse. • Ties back to IRT basics • IRT in education – If all the questions are equally discriminative and difficult, IRT doesn’t add much • IRT useful when we have a diverse set of questions and we want to know • Which questions are more discriminative • Which questions are difficult 34
- 35. Summary • Visualise thestrengths and weaknesses of algorithms • Select a portfolio of strong and weak algorithms • Understand more about algorithms • Anomalousness, stability, difficulty limit • Includes diagnostics • R package airt (on CRAN) • https://sevvandi.github.io/airt/ • Pre-print: http://bit.ly/algorithmirt • Comprehensive Algorithm Portfolio Evaluation using Item Response Theory • More applications included 35
- 36.