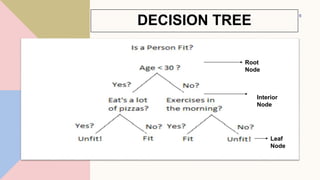
This document provides an overview of classification predictive modeling and decision trees. It discusses classification, including binary, multi-class, and multi-label classification. It then describes decision trees, including key terminology like root nodes, interior nodes, and leaf nodes. It explains how decision trees are built and parameters like max_depth and min_samples_leaf. Finally, it compares regression and classification trees and discusses advantages and disadvantages of decision trees.

1. CLASSIFICATION
Dr. Amanpreet Kaur​
Associate Professor,
Chitkara University,
Punjab

2. AGENDA
Introduction​
Primary goals
​Areas of growth
Timeline
​Summary​

3. CLASSIFICATION
• Classification predictive modeling involves assigning a
class label to input examples.
• Binary classification refers to predicting one of two classes
and multi-class classification involves predicting one of
more than two classes.
• Multi-label classification involves predicting one or more
classes for each example and imbalanced classification
refers to classification tasks where the distribution of
examples across the classes is not equal.
• Examples of classification problems include:
• Given an example, classify if it is spam or not.
• Given a handwritten character, classify it as one of the known
characters.
• Given recent user behavior, classify as churn or not.
3

4. •Text categorization (e.g., spam filtering)
•Fraud detection
•Optical character recognition
•Machine vision (e.g., face detection)
•Natural-language processing
• (e.g., spoken language understanding)
•Market segmentation
• (e.g.: predict if customer will respond to promotion)
•Bioinformatics
•(e.g., classify proteins according to their function)
4
EXAMPLE OF
CLASSIFICATION

5. DECISION TREE
• The decision tree algorithm builds the classification
model in the form of a tree structure.
• It utilizes the if-then rules which are equally exhaustive
and mutually exclusive in classification.
• The process goes on with breaking down the data into
smaller structures and eventually associating it with an
incremental decision tree.
• The final structure looks like a tree with nodes and
leaves. The rules are learned sequentially using the
training data one at a time.
• Each time a rule is learned, the tuples covering the
rules are removed. The process continues on the
training set until the termination point is met.
5

6. 6
DECISION TREE
Root
Node
Interior
Node
Leaf
Node

7. • Terminologies Related to Decision Tree Algorithms
• Root Node: This node gets divided into different homogeneous
nodes. It represents entire sample.
• Splitting: It is the process of splitting or dividing a node into two
or more sub-nodes.
• Interior Nodes: They represent different tests on an attribute.
• Branches: They hold the outcomes of those tests.
• Leaf Nodes: When the nodes can’t be split further, they are
called leaf nodes.
• Parent and Child Nodes: The node from where sub-nodes are
created is called a parent node. And, the sub-nodes are called
the child nodes.
7
DECISION TREE

8. DECISIONTREE
CLASSIFIER ()
• DecisionTreeClassifier (): It is nothing but the decision tree
classifier function to build a decision tree model in Machine
Learning using Python. The DecisionTreeClassifier() function
looks like this:
• DecisionTreeClassifier (criterion = ‘gini’, random_state =
None, max_depth = None, min_samples_leaf =1)
• Here are a few important parameters:
• criterion: It is used to measure the quality of a split in the
decision tree classification. By default, it is ‘gini’; it also supports
‘entropy’.
• max_depth: This is used to add maximum depth to the
decision tree after the tree is expanded.
• min_samples_leaf: This parameter is used to add the
minimum number of samples required to be present at a leaf
node.
8

9. DECISION TREE
REGRESSOR ()
• DecisionTreeRegressio (): It is the decision tree regressor function used to
build a decision tree model in Machine Learning using Python. The
DecisionTreeRegressor () function looks like this:
• DecisionTreeRegressor (criterion = ‘mse’, random_state =None ,
max_depth=None, min_samples_leaf=1,)
• criterion: This function is used to measure the quality of a split in the decision
tree regression. By default, it is ‘mse’ (the mean squared error), and it also
supports ‘mae’ (the mean absolute error).
• max_depth: This is used to add maximum depth to the decision tree after the
tree is expanded.
• min_samples_leaf: This function is used to add the minimum number of
samples required to be present at a leaf node.
9

10. GAINS CHART
From left to right:
• Node 6: 16% of policies, 35% of claims.
• Node 4: add’l 16% of policies, 24% of claims.
• Node 2: add’l 8% of policies, 10% of claims.
• ..etc.
– The steeper the gains chart, the stronger the
model.
– Analogous to a lift curve.
– Desirable to use out-of-sample data.
10

11. SPLITTING RULES
• Select the variable value (X=t1) that produces the
greatest “separation” in the target variable.
• “Separation” defined in many ways.
– Regression Trees (continuous target): use sum of squared errors.
– Classification Trees (categorical target): choice of entropy, Gini measure,
“twoing” splitting rule.
11

12. REGRESSION TREES
• Tree-based modeling for continuous target
variable
• most intuitively appropriate method for loss
ratio analysis
• Find split that produces greatest separation in
∑[y – E(y)]2
• i.e.: find nodes with minimal within variance
• and therefore greatest between variance
• like credibility theory
12

13. CLASSIFICATION TREES
• Tree-based modeling for discrete target
variable
• In contrast with regression trees, various
measures of purity are used
• Common measures of purity:
• Gini, entropy, “twoing”
• Intuition: an ideal retention model would
produce nodes that contain either defectors
only or non-defectors only
13

14. REGRESSION VS. CLASSIFICATION
TREES
14
• Splitting Criteria:
– Gini, Entropy, Twoing
• Goodness of fit measure:
– misclassification rates
• Prior probabilities and misclassification costs
– available as model “tuning parameters”
• Splitting Criterion:
– sum of squared errors
• Goodness of fit:
– same measure!
– sum of squared errors
• No priors or misclassification costs…
– … just let it run

15. HOW CART SELECTS THE
OPTIMAL TREE
• Use cross-validation (CV) to select the optimal
decision tree.
• Built into the CART algorithm.
– Essential to the method; not an add-on
• Basic idea: “grow the tree” out as far as you can….
Then “prune back”.
• CV: tells you when to stop pruning.
15

16. GROWING AND
PRUNING
• One approach: stop growing the tree early.
• But how do you know when to stop?
• CART: just grow the tree all the way out; then prune back.
• Sequentially collapse nodes that result in the smallest
change in purity.
• “weakest link” pruning.
16

17. CART ADVANTAGES
• Nonparametric (no probabilistic assumptions)
• Automatically performs variable selection
• Uses any combination of continuous/discrete variables
– Very nice feature: ability to automatically bin massively
categorical variables into a few categories.
• zip code, business class, make/model…
• Discovers “interactions” among variables
– Good for “rules” search
– Hybrid GLM-CART models
17

18. CART DISADVANTAGES
• The model is a step function, not a continuous score
• So if a tree has 10 nodes, yhat can only take on 10 possible values.
• MARS improves this.
• Might take a large tree to get good lift
• But then hard to interpret
• Data gets chopped thinner at each split
• Instability of model structure
• Correlated variables  random data fluctuations could result in
entirely different trees.
• CART does a poor job of modeling linear structure
18

19. USES OF CART
• Building predictive models
– Alternative to GLMs, neural nets, etc
• Exploratory Data Analysis
– Breiman et al: a different view of the data.
– You can build a tree on nearly any data set with
minimal data preparation.
– Which variables are selected first?
– Interactions among variables
– Take note of cases where CART keeps re-splitting the
same variable (suggests linear relationship)
• Variable Selection
– CART can rank variables
– Alternative to stepwise regression 19

20. REFERENCES
E Books-
Peter Harrington “Machine Learning In Action”,
DreamTech Press
Ethem Alpaydın, “Introduction to Machine
Learning”, MIT Press
Video Links-
https://www.youtube.com/watch?v=atw7hUrg3_8
https://www.youtube.com/watch?v=FuJVLsZYkuE
20

21. THANK YOU
aman_preet_k@yahoo.co.in