The document discusses theoretical frameworks behind image compression and semantic search, focusing on techniques like singular value decomposition (SVD), eigenvalue decomposition, and their applications in various fields such as natural language processing and data compression. It outlines the process of using SVD for dimensionality reduction to enhance semantic search capabilities and provides a step-by-step example of ranking documents based on relevance to a query. Furthermore, it highlights various computational methods and references essential literature in the field.

1. Theory behind Image Compression
and Semantic Search
Santi Adavani, Ph.D.
www.rocketml.net
@adavanisanti

2. Bio
• 2016 - → Co-founder, RocketML
• 2008 - 2016 → Product Manager, Intel
• 2003 - 2008 → Ph.D., University of Pennsylvania
• 1999 - 2003 → B. Tech, IIT Madras
4/6/17 RocketML

3. • Singular Value Decomposition
• Eigenvalue decomposition
• Principal Component Analysis
• Latent Semantic Analysis
• Latent Semantic Index
• Proper Orthogonal Decomposition
4/6/17 RocketML

4. 4/6/17 RocketML

5. Use cases across multiple disciplines
• Natural Language Processing
• Image Processing
• Signal Processing
• Genomics
• Data compression
• Search
• Recommendation engines
• Matrix inversion
4/6/17 RocketML

6. Topics
• Vectors and Matrices
• Singular value decomposition
• Image Compression
• Semantic search
4/6/17 RocketML

7. Vectors
4/6/17 RocketML
x1
x2
[2,2]
[2,1]
x1
x2
x3
[2,2,2]
x1, x2, x3, x4, … are features. In NLP, these are n-grams
2D 3D Hyper Space
[2,3,3,5, … ]

8. Matrix Vector Multiplication
4/6/17 RocketML
2 0
0 1
1
1
=
2
1
x1
x2
[2,1][1,1]
Ax
x
A x Ax
2 0 0
0 1 2
x1
x2
x3
[1,1,2]
1
1
2
2
5
=
x1
x2
[2,5]
3D 2D
A x Ax
Stretching, Rotation
Stretching, Rotation,
dimension changes

9. 4/6/17 RocketML
v
A v A2v A3v
Special vectors
Only Stretching, No Rotation

10. 4/6/17 RocketML
v
A v
A2v
A3v
Special vectors
Only Stretching, No Rotation

11. 4/6/17 RocketML
Example
5√5 𝑎𝑛𝑑 1/√5,2/√5 𝑓𝑜𝑟𝑚 𝑎𝑛 𝑒𝑖𝑔𝑒𝑛𝑣𝑎𝑙𝑢𝑒, 𝑒𝑖𝑔𝑒𝑛𝑣𝑒𝑐𝑡𝑜𝑟 𝑝𝑎𝑖𝑟 𝑜𝑓 𝐴
1 2
8 1
=
1
2
1/√5
2/√5
5√5𝐴𝑣 = 𝜆𝑣 5
10
=

12. Eigen decomposition for square matrices
4/6/17 RocketML
Q is a square matrix whose ith column is the eigenvector qi of A
L is a diagonal matrix where ith element is the ith eigenvalue
If A is symmetric i.e, A = AT
𝐴 = 𝑄 Λ 𝑄?@
𝐴 = 𝑄 Λ 𝑄A

13. Singular Value Decomposition of a matrix
4/6/17 RocketML
𝑀 = 𝑈 𝑆 𝑉
∗
𝑈, 𝑉 𝑎𝑟𝑒 𝑙𝑒𝑓𝑡 𝑎𝑛𝑑 𝑟𝑖𝑔ℎ𝑡 𝑠𝑖𝑛𝑔𝑢𝑙𝑎𝑟 𝑣𝑒𝑐𝑡𝑜𝑟𝑠
S 𝑖𝑠 𝑎 𝑑𝑖𝑎𝑔𝑜𝑛𝑎𝑙 𝑚𝑎𝑡𝑟𝑖𝑥 𝑤𝑖𝑡ℎ 𝑟𝑒𝑎𝑙 𝑠𝑖𝑛𝑔𝑢𝑙𝑎𝑟 𝑣𝑎𝑙𝑢𝑒𝑠
𝑈 𝑈∗ = 𝐼, 𝑉 𝑉∗ = 𝐼

14. SVD relation to eigenvalue decomposition
4/6/17 RocketML
• 𝐶𝑜𝑙𝑢𝑚𝑛𝑠 𝑜𝑓 𝑉 𝑎𝑟𝑒 𝑒𝑖𝑔𝑒𝑛𝑣𝑒𝑐𝑡𝑜𝑟𝑠 𝑜𝑓 𝑀∗
𝑀
• 𝐶𝑜𝑙𝑢𝑚𝑛𝑠 𝑜𝑓 𝑈 𝑎𝑟𝑒 𝑒𝑖𝑔𝑒𝑛𝑣𝑒𝑐𝑡𝑜𝑟𝑠 𝑜𝑓 𝑀𝑀∗
• 𝐸𝑙𝑒𝑚𝑒𝑛𝑡𝑠 𝑜𝑓 𝑆 𝑎𝑟𝑒 𝑠𝑞𝑢𝑎𝑟𝑒 𝑟𝑜𝑜𝑡𝑠 𝑜𝑓 𝑛𝑜𝑛 −
𝑧𝑒𝑟𝑜 𝑒𝑖𝑔𝑒𝑛𝑣𝑎𝑙𝑢𝑒𝑠 𝑜𝑓 𝑀∗
𝑀 𝑜𝑟 𝑀𝑀∗
𝑀∗
𝑀 = 𝑉 Σ∗
𝑈∗
𝑈 Σ𝑉∗
= 𝑉 Σ∗
Σ 𝑉∗
𝑀 𝑀∗
= 𝑈 Σ𝑉∗
𝑉 Σ∗
𝑈∗
= 𝑈 ΣΣ∗
𝑈∗

15. Dimension reduction
4/6/17 RocketML
Image
255 255255 255
255 255255 255
255 255255 255
255 255255 255
Matrix
200 pixels
200 pixels

16. Dimension reduction
4/6/17 RocketML
255 255255 255
255 255255 255
255 255255 255
255 255255 255 c
c
c
c
51000
c c c c
=
U UTS
C = -0.0707, Rank of this matrix = 1

17. Reconstruction
4/6/17 RocketML
450x400 pixels
90 90 89 90 …
90 90 89 90 …
123 94 101

18. Singular value decomposition
4/6/17 RocketML
𝑈 𝑖𝑠 450 𝑥 450 𝑜𝑟𝑡ℎ𝑜𝑛𝑜𝑟𝑚𝑎𝑙 𝑚𝑎𝑡𝑟𝑖𝑥
Σ 𝑖𝑠 450 𝑥 400 𝑚𝑎𝑡𝑟𝑖𝑥 𝑤𝑖𝑡ℎ
several 𝑧𝑒𝑟𝑜 𝑒𝑛𝑡𝑟𝑖𝑒𝑠
𝑉 𝑖𝑠 400 𝑥 400 𝑜𝑟𝑡ℎ𝑜𝑛𝑜𝑟𝑚𝑎𝑙 𝑚𝑎𝑡𝑟𝑖𝑥

19. Singular Values (Σ)
4/6/17 RocketML

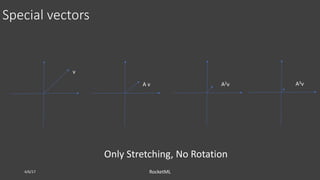
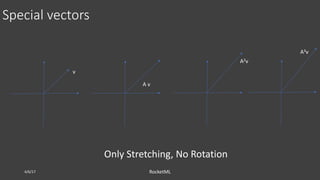
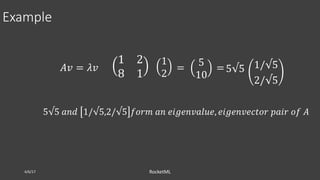
20. Reconstruction using few singular values
4/6/17 RocketML
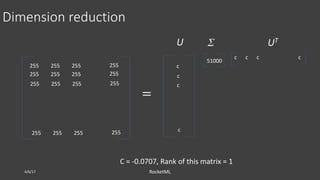
𝑈[: , 1: 2] 𝑆[1: 2] 𝑉[: , 1: 2] 𝑇 𝑈[: , 1: 3] 𝑆[1: 3] 𝑉[: , 1: 3] 𝑇

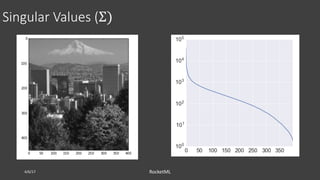
21. More singular values
4/6/17 RocketML
𝑈[: , 1: 20] ∗ 𝑆[1: 20] ∗ 𝑉[: , 1: 20] 𝑈[: , 1: 200] ∗ 𝑆[1: 200] ∗ 𝑉[: , 1: 200]

22. Normalize Cumulative Sum
4/6/17 RocketML
𝑆 = [ 𝜎
]
^
𝑠_ =
1
𝑆
[ 𝜎_
_?@
^

23. Top 200 singular values
4/6/17 RocketML

24. SVD can be used reduce the size of the data
while keeping most of the essence
4/6/17 RocketML
SVD gives access to important concepts in the
data.

25. Semantic Search
• Take a collection of the following documents
• Shipment of gold damaged in a fire.
• Delivery of silver arrived in a silver truck
• Shipment of gold arrived in a truck
• Problem: Rank these documents for the query “gold silver truck”
4/6/17 RocketML

26. Step 1: Bag of words
4/6/17 RocketML
• Shipment of gold damaged in a
fire.
• Delivery of silver arrived in a
silver truck
• Shipment of gold arrived in a
truck
𝐴 = 11 𝑥 3
𝑎
𝑎𝑟𝑟𝑖𝑣𝑒𝑑
𝑑𝑎𝑚𝑎𝑔𝑒𝑑
𝑑𝑒𝑙𝑖𝑣𝑒𝑟𝑦
𝑓𝑖𝑟𝑒
𝑔𝑜𝑙𝑑
𝑖𝑛
𝑜𝑓
𝑠ℎ𝑖𝑝𝑚𝑒𝑛𝑡
𝑠𝑖𝑙𝑣𝑒𝑟
𝑡𝑟𝑢𝑐𝑘
1 1 1
0 1 1
1 0 0
0 1 0
1 0 0
1 0 1
1 1 1
1 1 1
1 0 1
0 2 0
0 1 1
𝐴 =
Words Sentences

27. 4/6/17 RocketML
1 1 1
0 1 1
1 0 0
0 1 0
1 0 0
1 0 1
1 1 1
1 1 1
1 0 1
0 2 0
0 1 1
𝐴 =
Step 2: Singular Value Decomposition (SVD)
𝑈 𝑖𝑠 11𝑥 3 𝑜𝑟𝑡ℎ𝑜𝑛𝑜𝑟𝑚𝑎𝑙 𝑚𝑎𝑡𝑟𝑖𝑥
𝑆 𝑖𝑠 3𝑥3 𝑚𝑎𝑡𝑟𝑖𝑥
𝑉 𝑖𝑠 3𝑥3 𝑚𝑎𝑡𝑟𝑖𝑥
11𝑥 3 3 𝑥 3 3 𝑥 3
𝑈 Σ Vc=

28. 4/6/17 RocketML
1 1 1
0 1 1
1 0 0
0 1 0
1 0 0
1 0 1
1 1 1
1 1 1
1 0 1
0 2 0
0 1 1
𝐴 =
Step 3: Truncated SVD
𝑈′ 𝑖𝑠 11𝑥 2 𝑜𝑟𝑡ℎ𝑜𝑛𝑜𝑟𝑚𝑎𝑙 𝑚𝑎𝑡𝑟𝑖𝑥
𝑆′ 𝑖𝑠 2𝑥2 𝑚𝑎𝑡𝑟𝑖𝑥
𝑉′ 𝑖𝑠 2𝑥2 𝑚𝑎𝑡𝑟𝑖𝑥
11𝑥 2 2 𝑥 2 2 𝑥 2
𝑈′ Σ′ 𝑉eA=

29. Step 4: Find new query vector in reduced 2-
dimension space
4/6/17 RocketML
“𝑔𝑜𝑙𝑑 𝑠𝑖𝑙𝑣𝑒𝑟 𝑡𝑟𝑢𝑐𝑘”
0
0
0
0
0
1
0
0
0
1
1
q =
𝑎
𝑎𝑟𝑟𝑖𝑣𝑒𝑑
𝑑𝑎𝑚𝑎𝑔𝑒𝑑
𝑑𝑒𝑙𝑖𝑣𝑒𝑟𝑦
𝑓𝑖𝑟𝑒
𝑔𝑜𝑙𝑑
𝑖𝑛
𝑜𝑓
𝑠ℎ𝑖𝑝𝑚𝑒𝑛𝑡
𝑠𝑖𝑙𝑣𝑒𝑟
𝑡𝑟𝑢𝑐𝑘
𝑞e
= 𝑞 𝑈eA
𝑆e?@
𝑞′ = [−0.21, −0.1821]

30. Step 5: Rank documents based on cosine
similarity
4/6/17 RocketML
−0.4945 −0.6458 −0.5817
0.6492 −0.7914 0.2469
𝑞′ = [−0.21, −0.1821]
Sentences
[ −0.0541 0.9910 0.4478]
1 23

31. Search Results for “gold silver truck” using LSI
1. Delivery of silver arrived in a silver truck
2. Shipment of gold arrived in a truck
3. Shipment of gold damaged in a fire.
4/6/17 RocketML
Semantic Search or Concept based search

32. SVD can be used to reduce size of the data
while keeping most of the essence
4/6/17 RocketML
SVD gives access to important concepts in the
data.

33. Variations
• Singular Value Decomposition
• Eigenvalue decomposition
• Principal Component Analysis
• Latent Semantic Analysis
• Latent Semantic Index
• Proper orthogonal Decomposition
4/6/17 RocketML

34. Methods to compute SVD
• Arnoldi method with explicit restart and deflation
• Lanczos with explicit restart and deflation
• Krylov-Schur
• Generalized Davidson
• Randomized SVD
• Frequent Directions
4/6/17 RocketML
Matrix Computations (Johns Hopkins Studies in Mathematical Sciences)(3rd Edition) 3rd Edition
by Gene H. Golub (Author), Charles F. Van Loan (Author)

35. Packages
• Numpy
• Scikit-learn
• Gensim
• ARPACK
• LAPACK
4/6/17 RocketML

36. References
• An Introduction to the Conjugate Gradient Method Without the
Agonizing Pain, Jonathan Richard Shewchuk
• An introduction to Latent Semantic Analysis, Thomas K Landauer et.
Al
• Latent Semantic Indexing (LSI) An Example
• Matrix Computations, Gene Golub and Charles F. Van Loan
4/6/17 RocketML

37. Q&A
4/6/17 RocketML

38. 4/6/17 RocketML

39. 4/6/17 RocketML