Download as PDF, PPTX
Uploaded bySanti Adavani
From Genomics to NLP: One algorithm to rule them all
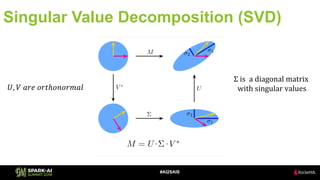
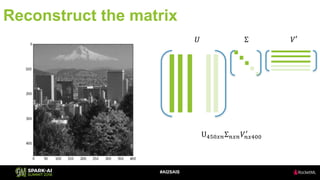
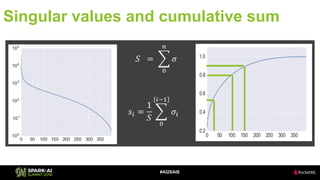
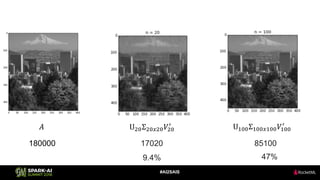
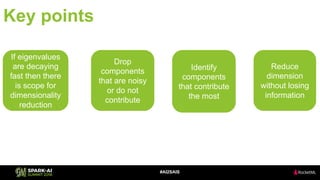
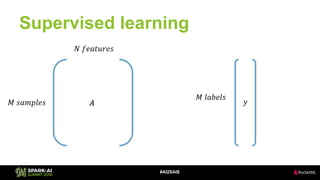
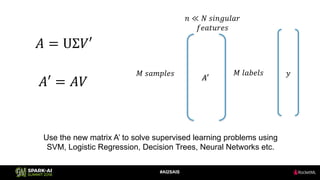
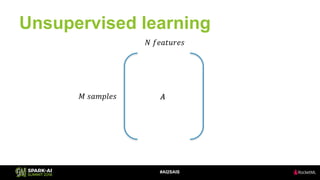
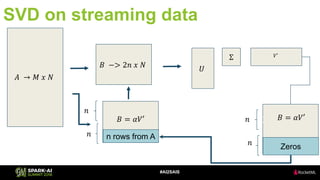
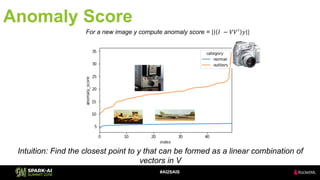
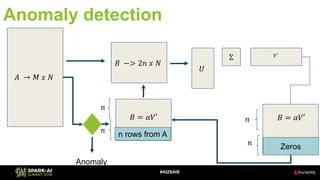
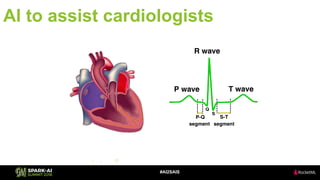
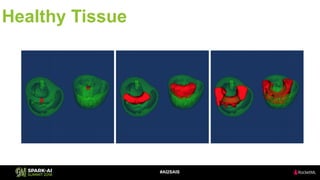
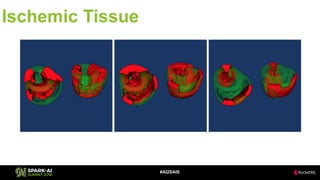
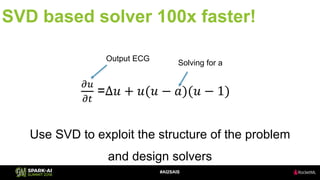
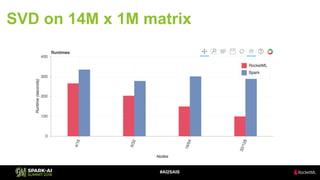
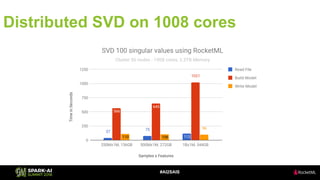
The document discusses the application of Singular Value Decomposition (SVD) across various domains, including genomics and natural language processing. It emphasizes dimensionality reduction techniques while maintaining essential information, and highlights its significance in supervised and unsupervised learning. Additionally, it outlines the use of SVD for solving problems in medical diagnostics and streamlining data processing using distributed systems.
From Genomics to NLP: One algorithm to rule them all
- 1. Santi Adavani/Vinay Rao Rocketml.net @rocketml FromGenomics to NLP: One algorithm to rule them all #AI2SAIS
- 2.
- 3. Outline • Introduction • Makingsense of SVD • One algorithm to rule them all • Scale out SVD #AI2SAIS
- 4.
- 5. Singular Value Decomposition(SVD) #AI2SAIS 𝑈, 𝑉 𝑎𝑟𝑒 𝑜𝑟𝑡ℎ𝑜𝑛𝑜𝑟𝑚𝑎𝑙 Σ is a diagonal matrix with singular values
- 6. Others in thesame family Principal component analysis (PCA) Eigenvalue decomposition Latent Semantic Indexing (LSI) Latent Semantic Analysis (LSA) #AI2SAIS
- 7. Outline • Introduction • Makingsense of SVD • One algorithm to rule them all • Scale out SVD #AI2SAIS
- 8. Making sense ofSVD #AI2SAIS
- 9.
- 10. Reconstruct the matrix UABCDGΣGDG𝑉GDACC E 𝑈 Σ 𝑉′ #AI2SAIS
- 11. Singular values andcumulative sum #AI2SAIS
- 12. UABCDHΣHDH 𝑉HDACC E UABCDIΣIDI𝑉IDACC E 𝐴 #AI2SAIS
- 13. UHCΣHCDHC 𝑉HC E UKCCΣKCCDKCC𝑉KCC E 180000 8510017020 9.4% 47% 𝐴 #AI2SAIS
- 14.
- 15. Key points #AI2SAIS Reduce dimension without losing information Drop components thatare noisy or do not contribute Identify components that contribute the most If eigenvalues are decaying fast then there is scope for dimensionality reduction
- 16. Outline • Introduction • Makingsense of SVD • One algorithm to rule them all • Scale out SVD #AI2SAIS
- 17.
- 18.
- 19.
- 20. #AI2SAIS 𝐴′ 𝑀 𝑠𝑎𝑚𝑝𝑙𝑒𝑠 𝑛 ≪ 𝑁 𝑠𝑖𝑛𝑔𝑢𝑙𝑎𝑟 𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠 𝑀 𝑙𝑎𝑏𝑒𝑙𝑠𝑦 𝐴 = UΣ𝑉′ 𝐴′ = 𝐴𝑉 Use the new matrix A’ to solve supervised learning problems using SVM, Logistic Regression, Decision Trees, Neural Networks etc.
- 21.
- 22.
- 23. #AI2SAIS 𝐴′ 𝑀 𝑠𝑎𝑚𝑝𝑙𝑒𝑠 𝑛 ≪ 𝑁 𝑠𝑖𝑛𝑔𝑢𝑙𝑎𝑟 𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠 𝐴= UΣ𝑉′ 𝐴′ = 𝐴𝑉 Use the new matrix A’ for clustering, nearest-neighbors, anomaly detection
- 24. 𝐴 → 𝑀 𝑥 𝑁 𝐵 −> 2𝑛 𝑥 𝑁 𝑈 Σ 𝑉′ Zeros K Randomized SVD 𝐵 = 𝛼𝑉′ Randomized SVD 𝑛 𝑛 K𝑛 𝑛 𝐵 = 𝛼𝑉′ n rows from A SVD on streaming data #AI2SAIS
- 25.
- 26.
- 27. Steps Create a datamatrix A using normal images and compute SVD Image 1 Image 2 Image N #AI2SAIS
- 28. Anomaly Score For anew image y compute anomaly score = | 𝐼 − 𝑉𝑉E 𝑦 | Intuition: Find the closest point to y that can be formed as a linear combination of vectors in V #AI2SAIS
- 29. 𝐴 → 𝑀 𝑥 𝑁 𝐵 −> 2𝑛 𝑥 𝑁 𝑈 Σ 𝑉′ Zeros K Randomized SVD 𝐵 = 𝛼𝑉′ Randomized SVD 𝑛 𝑛 K𝑛 𝑛 𝐵 = 𝛼𝑉′ n rows from A Anomaly detection #AI2SAIS Anomaly
- 30.
- 31. AI to assistcardiologists #AI2SAIS
- 32. Problem formulation Forward ProblemInverse problem #AI2SAIS ab ac =Δ𝑢 + 𝑢(𝑢 − 𝑎)(𝑢 − 1) Solving for u Given a ab ac =Δ𝑢 + 𝑢(𝑢 − 𝑎)(𝑢 − 1) Given u (ECG) Solving for a
- 33.
- 34.
- 35. SVD based solver100x faster! #AI2SAIS Use SVD to exploit the structure of the problem and design solvers ab ac =Δ𝑢 + 𝑢(𝑢 − 𝑎)(𝑢 − 1) Output ECG Solving for a
- 36. Outline • Introduction • Makingsense of SVD • One algorithm to rule them all • Scale out SVD #AI2SAIS
- 37. SVD on 14Mx 1M matrix #AI2SAIS
- 38. Distributed SVD on1008 cores #AI2SAIS
- 39.
- 40.