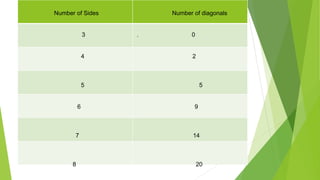
This document discusses problem solving and reasoning in mathematics. It outlines various problem solving strategies and techniques including understanding the problem, devising a plan, carrying out the plan, and checking answers. Examples are provided to illustrate applying these steps to word problems involving ages, ratios, and logic puzzles. Different problem solving approaches are described such as looking for patterns, making organized lists, guessing and checking, using tables, and working backwards. The document also discusses inductive and deductive reasoning as well as recreational math problems.

1. PROBLEM SOLVING AND
REASONING

2. OBJECTIVES:
 Problems in Mathematics prior to be detailed
discussion.
 Inductive and Deductive Reasoning
 Organize one's methods and procedure for
proving and solving problems
 Applying Mathematical logic
 Perform operations on Mathematical expression
correct
 Problem solving strategies
 Recreational Problems.

3. What is a problem?
A Problem is a statement requiring a
solution, usually by means of
mathematical operation/ geometric
construction.

4. METHOD,
ANSWER, AND
SOLUTION

5. Problem solving plays a very
important role in mathematics
learning. It helps the learners
think critically. Problem solving
involves translation of word
statements into mathematical
expressions or equations.

7. As suggested by George Polya,
problem solving follows a simple
set of steps or guide stated
below:
1. Understand the problem.
2. Devise a plan.
3. Carry out the plan.
4. Look back and check.

8. APPLYING THE STEPS:
Example: Twice the difference of a number and 1 is
4 more than that number. Find the number.
 Step 1: Understand the problem.
Make sure that you read the question carefully
several times. Since we are looking for a number,
we will let x = a number.
 Step 2: Devise a plan.
You need to translate it into a mathematical
sentence. Twice the difference of a number and 1 is
4 more than that number is 2 (x – 1) = x + 4.

9.  Step 3: Carry out the plan.
Solve the mathematical sentence.
2 (x – 1) = x + 4
2x – 2 = x + 4
2x – 2 – x = x + 4 – x
x – 2 = 4
x – 2 + 2 = 4 + 2
x = 6
 Step 4: Look back and check.
Interpret the problem.
If you take twice the difference of 6 and 1, you’ll get 10;
you’ll get the same as 4 more than 6. Therefore, 6 is indeed
the number that you’re looking for.

10. PROBLEM SOLVING STRATEGIES
 1. Look for a pattern.
Example: Find the sum of the first 100 even positive numbers.
Solution:
The sum of the first 1 even positive numbers is 2 or 1 (1 + 1) = 1 (2). The
sum of the first 2 even positive numbers is 2 + 4 = 6 or 2 (2 + 1) = 2 (3).
The sum of the first 3 even positive numbers is 2+ 4 + 6 = 12 or 3 (3 + 1) = 3
(4).
The sum of the first 4 even positive numbers is 2 + 4 + 6 + 8 = 20 or 4(4+1).
Look for a pattern in the problem: The sum of the first 100 even positive
numbers is 2 + 4 + 6 + … = x.
 2. Make an organized list.
Example: Find the median of the following test scores: 73, 65, 82, 78, and 93.
Solution:
Make a list from smallest to largest: 65, 73, 78, 82, 93
Since 78 is the middle number, the median is 78.

11.  3. Guess and Check.
Example: Which of the numbers 4, 5, or 6 is a solution to (n + 3) (n – 2) = 36?
Solution:
Subsnumbertitute each number for “n” in the equation. Six is the solution since (6 +
3)
(6 – 2) = 36.
4. Make a table.
Example: How many diagonals does a 13-gon have?
Solution:
Make a table based on the problem or question.

12. Number of Sides Number of diagonals
3 . 0
4 2
5 5
6 9
7 14
8 20

13.  5. Work backwards.
Example: Fortune Problem: a man died and left the following instructions
for his fortune,
half to his wife; 1/7 of what was left went to his son; 2/3 of what was left
went to his butler;
the man’s pet pig got the remaining $2000. How much money did the man
leave behind
altogether?
Solution:
The pig received $2000.
1/3 of x = $2000
x = $6000
6/7 of x $6000
x = $7000
½ of x = $7000
x = $14,000

14. ILLUSTRATIVE EXAMPLES
Age Problem
A. Mercy is 5 years younger than Robert. How old are they in
two years?
Name Age Now Age in 2 Years
Mercy x - 5 x – 5 + 2 or x – 3
Robert x x + 2

15. B. Anthony is twice as old as Beth. How
old are they 3 years ago?
Name Age Now Age 3 Years Ago
Anthony 2x 2x – 3
Beth x x – 3

16. C. Mary who is 54 years old has a niece,
Abbie, who is 18 years old. In how many
years will Abbie’s age be 2/5 of her aunt’s
age?
Solution:
Let x be the required number of years
Name Age Now Age x Years from Now
Mary 54 54 + x
Albie 18 18 + x
Working Equation: (18 + x) = 2/5 (54 + x)

17.  18 + x = 2/5 (54 + x)
 18 + x = 2/5 (54) + 2/5x
 x – 2/5x = 2/5 (54) – 18
 3/5x = 18/5
 x = 6
 Therefore, in 6 years Abbie’s age will be 2/5
of his aunt’s age.

23. SOLVING LOGIC PUZZLES
A logical puzzle is a
problem that can be
solved through
deductive reasoning.

24. Solving logic puzzles is like taking
your brain to the gym. They exercise
parts of the brain that may not be
stimulated otherwise. Logic puzzles
boost brain activity, encourage
systematic thinking, build
confidence, reduce boredom, and so
much more

25. The murderer is number 3 because
the bathroom is for the ladies

26. PROBLEM SOLVING
with
PATTERNS

31. RECREATIONAL
PROBLEMS

36. THANK YOU!!!