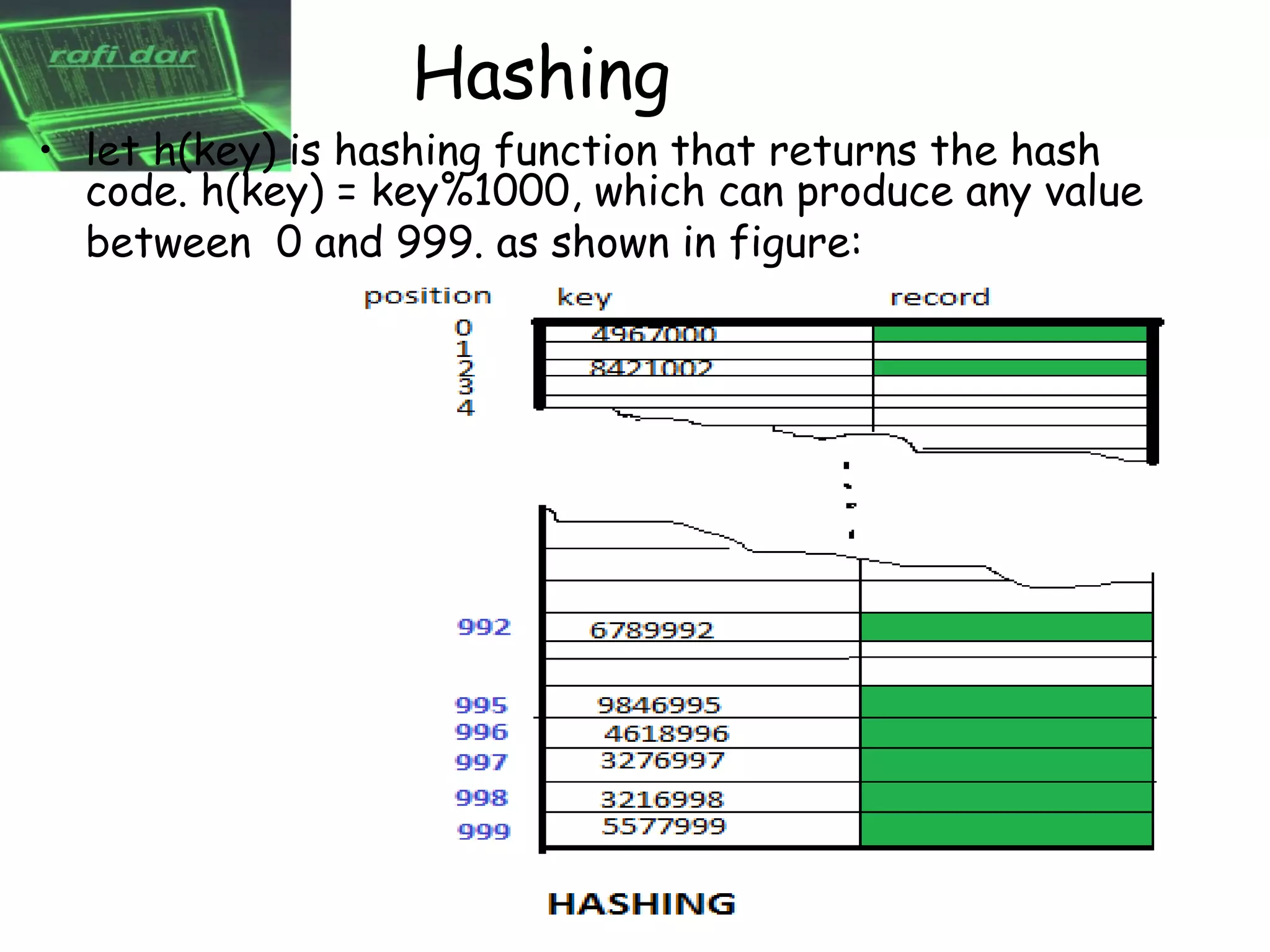
This document discusses hashing techniques for storing data in a hash table. It describes hash collisions that can occur when multiple keys map to the same hash value. Two primary techniques for dealing with collisions are chaining and open addressing. Open addressing resolves collisions by probing to subsequent table indices, but this can cause clustering issues. The document proposes various rehashing functions that incorporate secondary hash values or quadratic probing to reduce clustering in open addressing schemes.

1. • Concept Of hashing
• Need of Hashing
• Hash Collision
• Dealing with Hash Collision
• Resolving Hash Collisions by Open
Addressing
• Primary clustering
• Double Rehash

2. Concept Of hashing
• Hashing: hashing is a technique for performing almost
constant time in case of insertion deletion and find
operation.
• taking a very simple example, as array with its index
as key is the example of table.
• So each index (key) can be used for accessing values
in the constant search time.
• Mapping key must be simple to compute and must help
in identifying the associated records.
• Function that help us in generating such type of keys
is termed as Hash Function.

3. Hashing
• let h(key) is hashing function that returns the hash
code. h(key) = key%1000, which can produce any value
between 0 and 999. as shown in figure:

4. Need of Hashing
• Hashing maps large data sets of variable length to
smaller data sets of a fixed length. For example, an
inventory file of a company having more than 100
items and the key to each record is a seven digit part
number. To use direct indexing using entire seven
digit key, an array of 10 million elements would be
required. Which clearly is wastage of space, since
company is unlikely to stock more than few thousand
parts.
• Hence hashing provides an alternative to convert
seven digit key into an integer within limited range.
The values returned by a hash function are called
hash values, hash codes.

5. • Suppose two keys k1 and k2 hashes
such that h(k1) = h(k2). Here two
keys hashes into the same value and
are supposed to occupy same slot in
hash table ,which is unacceptable.
• Such a situation is termed as hash
collision.

6. Dealing with Hash Collision
• Two methods to deal with hash collision are:
• Rehashing and Chaining
Rehashing: invokes a secondary hash function
(say Rh(key)), which is applied successively until
an empty slot is found, where a record can be
placed.
Chaining: builds a Linked list of items whose key
hashes to same value. During search this short
linked list is traversed sequentially for the desired
key. This technique requires extra link field to
each table position.

7. hashing
Analysis:
• The worst case running time for insertion is
O(1).
• Deletion of an element x can be accomplished
in O(1) time if the lists are doubly linked.
• In the worst case behaviour of chain-hashing,
all n keys hash to the same slot, creating a
list of length n. The worst-case time for
search is thus θ(n) plus the time to compute
the hash function.

8. A good hash function is one that minimizes
collision and spreads the records uniformly
throughout the table. that is why it is
desirable to have larger array size than
actual number of records.
More formally, suppose we want to store
a set of size n in a table of size m. The
ratio α = n/m is called a load factor, that
is, the average number of elements stored
in a Table.

9. Resolving Hash Collisions by
Open Addressing
• Simplest method of resolving the hash
collision is to place record into the next
available position in the array.
• e.g. if key = 7803497.
• Then using hash function h(key) = key%
1000 will produce 497. However if the
497th position is already occupied by key =
2885497, then next available position is
chosen.
• The above technique is termed as Linear
probing.
• the approach however a some pitfall called
primary clustering problem.

10. • Primary clustering: the phenomenon
where two keys that hashes into
different values compete with each
other in successive rehashes. Primary
clustering is the result of the
formation of blocks of occupied
positions.

11. Eliminating primary
clustering
Solution 1: allow the rehash function to depend on
the number of times the particular function is
applied for hash value.
Rh(I,j) yields I the hash value if the key is being
rehashed for jth time.
ist rehash yeilds rh1 = rh(h(key),1)
2nd rehash yeilds rh2 =rh(rh1 +2)%tablesize and so
on.
Solution 2: rather than always moving one spot,
move i2 spots from the point of collision, where i is
the number of attempts to resolve the collision. Ie.
The rehash of h(key) will be (h(key)+ sqr(i))%table
size. The method is called as Quadratic Rehash.

12. Double Rehash
• Both the solutions for eliminating the primary
clustering suffers from another pitfall called
secondary clustering. A phenomenon in which two
keys hashes into same hash value then follows the
same rehash path.
• One way of eliminating all types of clustering is to
use double hash technique, which uses two hash
functions: h1(key) and h2(key). The h1(key)
determines the location for insertion, if occupied,
then rehash function rh(i+h2(key))%tablesize is
successively used untill an empty location is found.