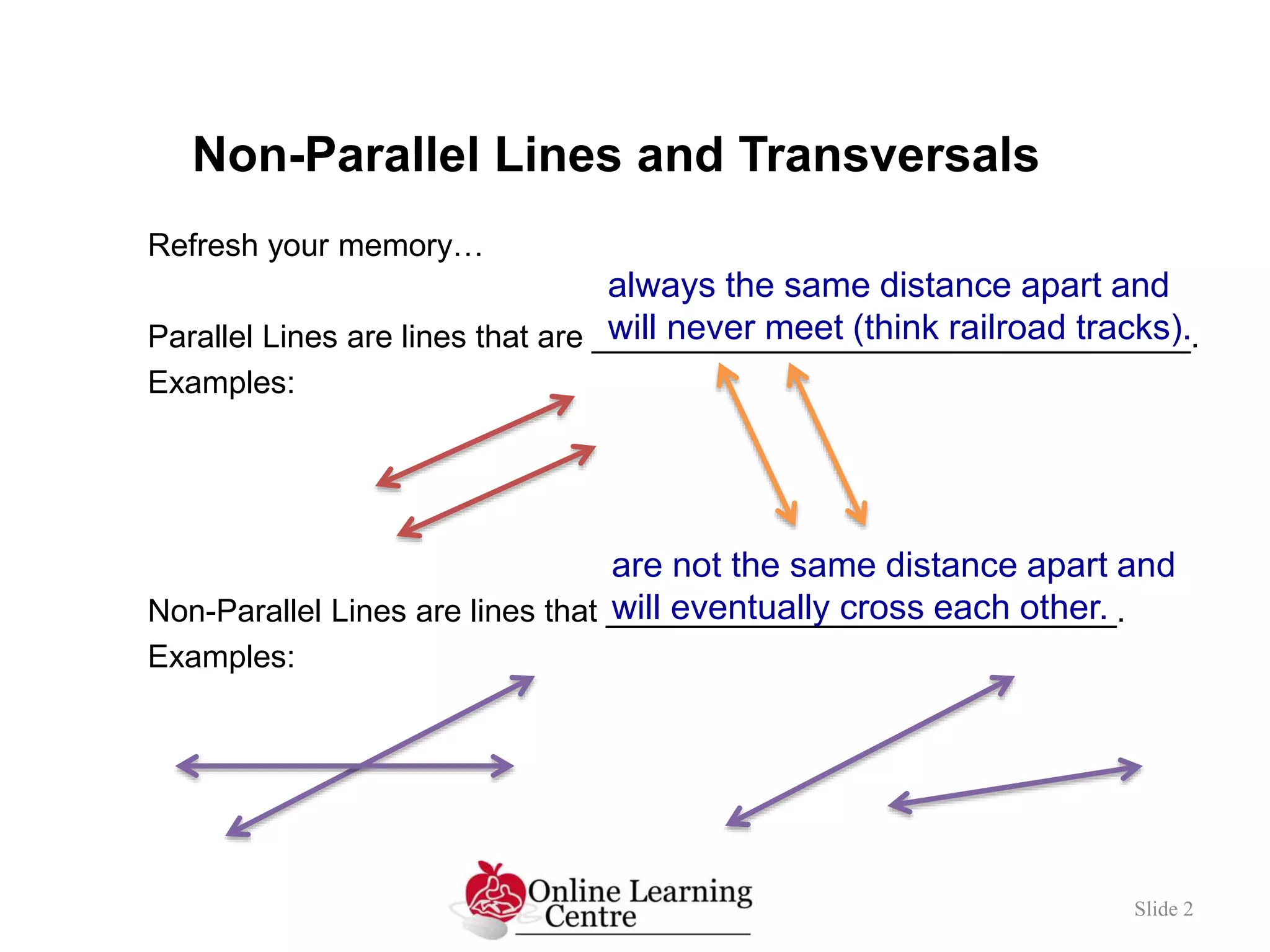
The document defines and provides examples of different types of angles formed by intersecting non-parallel lines and a transversal line, including corresponding angles, alternate interior angles, same-side interior angles, alternate exterior angles, and same-side exterior angles. Examples are given to identify specific angles that fit several of these categories using labeled diagram representations.

1. Non-Parallel Lines and Transversals
Slide 1
Refresh your memory…
Parallel Lines are lines that are __________________________________.
Examples:
Non-Parallel Lines are lines that _____________________________.
Examples:

2. Non-Parallel Lines and Transversals
Slide 2
Refresh your memory…
Parallel Lines are lines that are __________________________________.
Examples:
Non-Parallel Lines are lines that _____________________________.
Examples:
always the same distance apart and
will never meet (think railroad tracks).
are not the same distance apart and
will eventually cross each other.

3. Slide 3
Definitions:
Vertically Opposite Angles: angles created by intersecting lines that
share only a vertex.
Transversal: a line that intersects two or more lines.
m and n are vertically opposite angles
a and b are vertically opposite angles
transversal

4. Slide 4
Corresponding Angles: angles that occupy the same relative
position in two different intersections. (same side of transversal
and either above or below the lines)
Can you identify the pairs of
corresponding angles?
l1
l2
t
1 2
43
7
5 6
8

5. Slide 5
Corresponding Angles: angles that occupy the same relative
position in two different intersections. (same side of transversal
and either above or below the lines)
Can you identify the pairs of
corresponding angles?
1 and 5
1 and 5
Left of the
transversal
Above the lines
l1
l2
t
1 2
43
7
5 6
8

6. Slide 6
Corresponding Angles: angles that occupy the same relative
position in two different intersections. (same side of transversal
and either above or below the lines)
Can you identify the pairs of
corresponding angles?
3 and 7
3 and 7
Left of the
transversal
Below the lines
l1
l2
t
1 2
43
7
5 6
8

7. Slide 7
Corresponding Angles: angles that occupy the same relative
position in two different intersections. (same side of transversal
and either above or below the lines)
Can you identify the pairs of
corresponding angles?
2 and 6
2 and 6
Right of the
transversal
Above the lines
l1
l2
t
1 2
43
7
5 6
8

8. Slide 8
Corresponding Angles: angles that occupy the same relative
position in two different intersections. (same side of transversal
and either above or below the lines)
Can you identify the pairs of
corresponding angles?
4 and 8
4 and 8
Right of the
transversal
Below the lines
l1
l2
t
1 2
43
7
5 6
8

9. Slide 9
Corresponding Angles: angles that occupy the same relative
position in two different intersections. (same side of transversal
and either above or below the lines)
Can you identify the pairs of
corresponding angles?
1 and 5
3 and 7
2 and 6
4 and 8
1 and 5 3 and 7 2 and 6 4 and 8
Left of the
transversal
Left of the
transversal
Right of the
transversal
Right of the
transversal
Above the lines Below the lines Above the lines Below the lines
l1
l2
t
1 2
43
7
5 6
8

10. Slide 10
Interior: angles between the lines
Interior angles VS Exterior angles

11. Slide 11
Exterior: angles outside the lines
Interior angles VS Exterior angles

12. Slide 12
Interior: angles between the lines
Exterior: angles outside the lines
Interior angles VS Exterior angles

13. Slide 13
Alternate Interior Angles: angles in opposite positions between
two lines intersected by a transversal.
There are two pairs of
alternate interior angles.
3 and 6
4 and 5
l1
l2
t
1 2
43
7
5 6
8

14. Slide 14
Same-Side Interior Angles: angles on the interior AND on the
same side of the transversal.
There are two pairs of
same-side interior angles.
3 and 5
4 and 6
l1
l2
t
1 2
43
7
5 6
8

15. l1
l2
t
1 2
43
7
5 6
8
Slide 15
Alternate Exterior Angles: angles in opposite positions outside
two lines intersected by a transversal.
There are two pairs of
alternate exterior angles.
1 and 8
2 and 7

16. Slide 16
Same-Side Exterior Angles: angles that are on the same side of
the transversal AND outside the lines.
There are two pairs of
same-side exterior angles
1 and 7
2 and 8
l1
l2
t
1 2
43
7
5 6
8

17. Slide 17
Example 1: Identify two angles corresponding to 1. Name the
two lines and the transversal you are using.

18. Slide 18
Example 1: Identify two angles corresponding to 1. Name the
two lines and the transversal you are using.
Using lines 3 & 4 and
line 1 as the transversal,
1 and 7 are
corresponding angles.
transversal

19. Slide 19
Example 1: Identify two angles corresponding to 1. Name the
two lines and the transversal you are using.
Using lines 3 & 4 and
line 1 as the transversal,
1 and 7 are
corresponding angles.
Using lines 1 & 2 and
line 2 as the transversal,
1 and 3 are
corresponding angles.
transversal
transversal

20. Slide 20
Example 2: Identify a same-side interior angle to 10. Name
the two lines and the transversal you are using.

21. Slide 21
Example 2: Identify a same-side interior angle to 10. Name
the two lines and the transversal you are using.
Using lines 3 & 4 and line
2 as the transversal,
10 and 4 are
same-side interior angles.
transversal

22. Slide 22
Example 3: Identify an alternate interior angle to 5. Name the
two lines and the transversal you are using.

23. Slide 23
Example 3: Identify an alternate interior angle to 5. Name the
two lines and the transversal you are using.
Using lines 3 & 4 and
line 2 as the transversal,
5 and 10 are
alternate interior angles.
transversal

24. Slide 24
Example 4: Identify two same-side interior angles to 8. Name
the two lines and the transversal you are using.

25. Slide 25
Example 4: Identify two same-side interior angles to 8. Name
the two lines and the transversal you are using.
Using lines 3 & 4 and line
2 as the transversal,
8 and 5 are
same-side interior angles.
transversal

26. Slide 26
Example 4: Identify two same-side interior angles to 8. Name
the two lines and the transversal you are using.
Using lines 3 & 4 and line
2 as the transversal,
8 and 5 are
same-side interior angles.
transversal
Using lines 1 & 2 and line
4 as the transversal,
8 and 7 are
same-side interior angles.
transversal