This document summarizes an experiment that investigates the relationship between water pressure and flow rate. Water was flowed from a container through a small hole for timed intervals at varying water heights, and the resulting flow rate was measured. The data showed a proportional relationship between pressure difference and squared flow rate, supporting Bernoulli's equation. The slope of the line of best fit remained constant, as expected for this experimental setup. Limitations included the assumption of zero kinetic energy and challenges closing the hole precisely.

1. Non Sereeyothin
01/10/11
IB HL Physics Year 2
Pressure vs. Rate of Flow
Introduction:
Pressure is the exertion of force upon a unit area by a surface of an object in a perpendicular
direction.
[1]
Where is the density of water, is the gravity (acceleration), and is the height of water.
When fluid flows through pipe, there are two main forces acting on it. One is the frictional force
that is made by the side of the pipe, and the other one is the viscous force in the fluid. Near the
wall of the pipe, there is a thin layer of fluid that sticks to the pipe. In the middle of the pipe, the
water moves faster and consistently. The viscous force of fluid makes a shearing action which
will result in a small layer of fluid that will keep on increasing until it reach the speed of the free
flowing in the center of the pipe. The energy is lost from these two forces.
Ideal fluid has a steady flow, nonviscous flow, irrational flow, and incompressible flow. Steady
flow is when the particles flow after each other in a stream line and all particles has the same
velocity. Nonviscous flow is when there are no shearing forces in the fluid and will result in
producing heat as the fluid flows. Irrational flow is when there will be no turmoil in the form of
eddy currents or whirlpools. Incompressible flow is when the density of the fluid is constant.
Fluid pressure is defined as the pressure at some point within a fluid. This occurs in two different
conditions, one is an open condition (open channel flow) and the other one is a closed condition
(conduits). In an open condition, the pressure stays the same which follow the principle of fluid
statics. In a closed condition can be static when the fluid does not move and it can be dynamic
when the fluid can move in a pipe. This follows the principle of fluid dynamics. The fluid
pressure is a characteristic of the discoveries of Daniel Bernoulli. As the kinetic energy of the
water decreases, the pressure increases. When a cross sectional area of a pipe decreases, the
kinetic energy of water increases leading to a decrease in pressure. This is called the Bernoulli
Effect.
http://dev.physicslab.org/Document.aspx?doctype=3&filename=Fluids_Dynamics.xml

2. The equation for the flow rate of water coming out of the hole is shown below:
[2]
Where v is the velocity of the water, Q is the flow rate of the water, and A is the cross sectional
area of the hole. The equation for the pressure of the water inside the hole is shown below
(derived from Bernoulli’s equation).
[3]
Where is the pressure inside the container, is the pressure outside the container, is the
potential energy outside the hole, is the pressure of the atmosphere, is the density of water, is the
gravity at the surface of the water, is the height of water, and is the pressure of the water inside
the container.
Design:
Research Question:
How does the water pressure inside a cylindrical container affect its water flow rate?
Variables:
The independent variable is the water pressure inside the cylindrical container which is
controlled by the height of water in the container. The dependent variable is the water flow rate.
The controlled variables in this experiment was the amount of time per trials (10 seconds) which
can be measured using a stopwatch, the temperature of water using the same source of water, the
height where the experiment was done (constant acceleration or gravity), the cylindrical
container, and the density of water using the same source of water.

3. Materials and Procedure:
Cut a small 5.7 millimeter diameter hole on the side 7 centimeters above the bottom of the water
container. Use modeling clay to close the hole. Fill the water into the container only up to the most top
part of the largest diameter. Make sure that the water does not leak out or push the clay out. Stick the
meter stick into the middle of the container and measure the height of the water in the container. Start the
stopwatch and pull the clay out at the same time. Use 1000 ml graduated cylinder to catch the water
that’s leaking out of the hole. When the stopwatch reaches 10 seconds, close the hole on the water
container with the clay. Measure the height of the water in the container again and measure the height of
water in the 1000 ml graduated cylinder. Empty out the water in the graduated cylinder. Repeat these
italicize steps for the next five trials with different height of water in the container (ranging from 7 to 33
centimeters).
Water Container
Hole in the water container
1000 ml Graduated Cylinder
Figure 1: Shows the experimental setup. Note that the diameter of the hole is 5.7 mm and the concave
bump under the container is 3 cm high. The bottom of the container to the hole is 7 cm.
Data Collection and Processing:
Measured Height Attuned Average Height
(cm) ±0.2 (cm) ±0.4
Initial Final Average
7.4 6.6 7.0 3.0
10.2 9.3 9.8 5.8
15.5 14.5 15.0 11.0
20.8 19.7 20.3 16.3
26.7 25.5 26.1 22.1
32.4 30.8 31.6 27.6
Table 1: Shows the calculated heights of the water inside the container when doing the experiment. Note
that the calculated average height of water is found by subtracting the average height by 4 since there is a
small concave bump at the bottom of the container.

4. Change in Volume
(cm^3) ±9
Trial 1 Trial 2 Trial 3 Average
201 203 198 201
274 287 276 279
385 399 387 390
474 471 464 470
545 541 528 538
598 593 583 591
Table 2: Shows the average change in volume of the water that flows out of the hole.
Calculated
Average Flow
Average Pressure Average Flow Rate Squared
Rate
Difference
(Pa) ±40 (cm^3) ±9 (cm^6/s^2) ±100
290 20 400
560 28 800
1080 39 1520
1590 47 2200
2160 54 2900
2690 59 3500
Table 3: Shows the calculated average pressure difference and the average flow rate of the water.
Figure 2: Shows the quadratic relationship between the pressure and flow rate.

5. Figure 3: Shows the proportional relationship between the pressure and the flow rate squared.
Figure 4: Shows the high-low fit for the pressure and flow rate squared graph according to figure 3. The
range of the two slopes is 0.1 with an uncertainty of . The range of the two y-intercepts is 150 with
an uncertainty of

6. Sample Calculations:
Finding the attuned average height
Finding the calculated average pressure difference:
Finding the Uncertainty for the calculated average pressure difference:
Finding the Uncertainty for the change in volume:

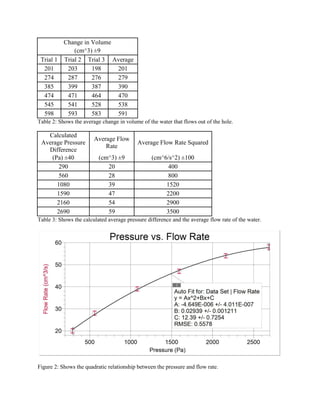
7. Finding the average flow rate of the water:
Finding the uncertainty for the average flow rate of the water:
Finding uncertainty of the average flow rate squared:
Conclusion:
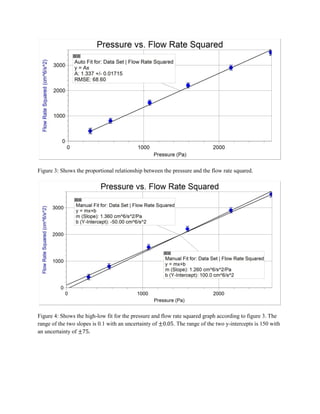
The relationship of the equation between the pressure and the water flow rate squared according
to figure 3 and figure 4 is shown below:
[4]
The equation 3 states that the relationship between the pressure and the water flow rate squared
should be proportional to each other. The results clearly support this relationship. This shows
that the results in this experiment are highly confident because the line of best fit in figure 3 goes
through all the data point in their uncertainties.

8. The slope of equation 4 is a constant and will remain constant even though the water flow
rate squared changes. This is because the density of water ( ) and the area of the hole ( ) are
constant. The y-intercept should be zero because if the pressure difference is zero, then the water
flow rate squared should be zero too due to the fact that the water does not flow out the container
resulting in a directly proportional relationship.
The limitation of this experiment only applies to water flowing out of a standard 5 gallon water
container with a small opening hole with a height of water ranging from 7 to 33 centimeters.
Evaluation:
A systematic error in this experiment is the kinetic energy of the water in the water container is
assumed to be zero. As the water flows out of the container, the water in the container would
decrease therefore the kinetic energy of the water cannot be zero. This could be improved by
using a high speed video camera to calculate the velocity of the water and the level of the water.
A human error in this experiment is the time taken to close the hole. It is very hard to close the
hole in an exact 10 seconds. There might be problems when closing the hole with modeling clay.
This error could be improved by using a smaller hole and a larger time frame.
Another error might be finding the pressure using the average height of the water. This is an
accurate way of measuring the pressure because if the height is measured in a more accurate
way, then the height must be measured every one second instead of ten seconds. This error could
be fixed by using a high speed video camera to measure the heights of water during each trials
and use this value to calculate the average height for ten seconds.