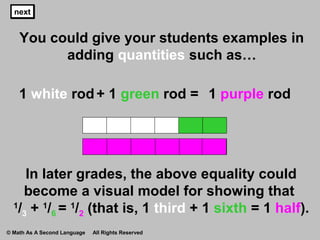
The document emphasizes the importance of understanding the relationship between quantities and units in arithmetic, particularly through the adjective/noun theme. By clarifying that numerators and denominators represent different aspects of numbers, the text aims to improve students' ability to add fractions and various quantities correctly. It suggests engaging activities like 'Guess My Noun' to reinforce these concepts in a fun and interactive manner.