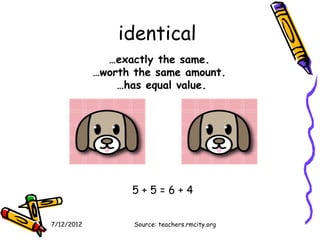
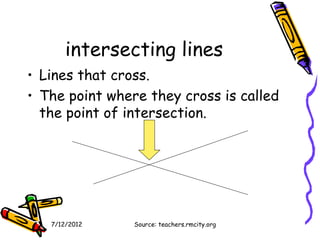
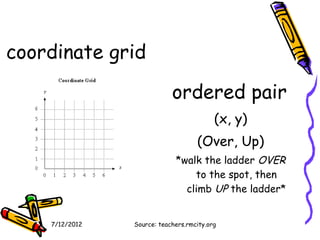
The document provides definitions and explanations of key math vocabulary terms related to numbers, operations, and geometry. Some terms defined include calculate, operation, evaluate, identical, standard form, expanded form, word form, natural numbers, digit, place value, period, inequality, infinite, line, line segment, ray, round number, approximate value, exact, estimate, polygon, vertex, perimeter, compatible numbers, commutative property, associative property, sum, summand, inverse, subtraction, difference, subtrahend, minuend, parentheses, numerical expression, algebraic expression, multiplication, factors, product, and commutative property of multiplication.