Download as PDF, PPTX
Uploaded byIsaac Yowetu
Gram schmidt orthogonalization | Orthonormal Process
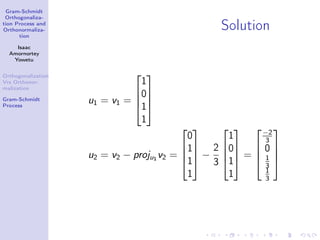
The document discusses Gram-Schmidt orthogonalization and orthonormalization. It defines orthogonalization as constructing orthogonal vectors that span a subspace, while orthonormalization results in unit vectors. The Gram-Schmidt process is described as a method to take a set of vectors and construct an orthogonal set from them. Two examples applying the Gram-Schmidt process are shown.
More Related Content
Gram schmidt orthogonalization | Orthonormal Process
- 1. Gram-Schmidt Orthogonalization Process andOrthonormalization Numerical Linear Algebra Isaac Amornortey Yowetu NIMS-GHANA September 22, 2020
- 2. Gram-Schmidt Orthogonaliza- tion Process and Orthonormaliza- tion Isaac Amornortey Yowetu Orthogonalization VrsOrthonor- malization Gram-Schmidt Process Outline 1 Orthogonalization Vrs Orthonormalization 2 Gram-Schmidt Process
- 3. Gram-Schmidt Orthogonaliza- tion Process and Orthonormaliza- tion Isaac Amornortey Yowetu Orthogonalization VrsOrthonor- malization Gram-Schmidt Process Orthogonalization Vrs Orthonormalization Orthogonalization It is a process of constructing a set of orthogonal vectors that span a particular subspace. Suppose we have a set of linearly independent set of vectors {v1, v2, ..., vn} ∈ V in the inner product space, we can construct a set of orthogonal bases vectors {u1, u2, ..., un} from the Inner Product or Euclidean space that will be of the same subspace such that: • the new set of vectors and the old set of vectors must have the same linear span. • every vector in the new set is orthogonal to every other vector in the new set.
- 4. Gram-Schmidt Orthogonaliza- tion Process and Orthonormaliza- tion Isaac Amornortey Yowetu Orthogonalization VrsOrthonor- malization Gram-Schmidt Process Orthonormalization It is a form of orthogonalization in which each resulting vector is a unit vector. Supppose {u1, u2, ..., un} as the orthogonal basis, then w1 = u1 ||u1|| , w2 = u2 ||u2|| , ..., wn = un ||un|| of which {w1, w2, ..., wn} be the orthonormal basis. some Orthogonalization Algorithms • Gram-Schmidt Process • Householder Transformation • Givens Rotation Theorem Any orthogonal set is linearly independent.
- 5. Gram-Schmidt Orthogonaliza- tion Process and Orthonormaliza- tion Isaac Amornortey Yowetu Orthogonalization VrsOrthonor- malization Gram-Schmidt Process Gram-Schmidt Process Many Vectors Considering a vector space V in an inner product space. And {v1, v2, ...vn} be a basis for V, then: u1 = v1 (1) u2 = v2 − < u1, v2 > < u1, u1 > u1 (2) u3 = v3 − < u1, v3 > < u1, u1 > u1 − < u2, v3 > < u2, u2 > u2 (3) ... = · · · · · · · · · · · · · · · (4) un = vn − < u1, vn > < u1, u1 > u1−, ..., − < un−1, vn > < un−1, un−1 > un−1 (5)
- 6. Gram-Schmidt Orthogonaliza- tion Process and Orthonormaliza- tion Isaac Amornortey Yowetu Orthogonalization VrsOrthonor- malization Gram-Schmidt Process Gram-Schmidt Process Solved Problems Example 1 Apply Gram-Schmidt orthogonalization process to the sequence of vectors in R3 , and hence, find the orthonormal basis. v1 = 1 1 1 , v2 = 1 2 0 , v3 = 2 0 1
- 7. Gram-Schmidt Orthogonaliza- tion Process and Orthonormaliza- tion Isaac Amornortey Yowetu Orthogonalization VrsOrthonor- malization Gram-Schmidt Process Solution u1 = v1 = 1 1 1 u2 = v2 − proju1 (v2) = 1 2 0 − 3 3 1 1 1 = 0 1 −1 u3 = v3 − proju1 (v3) − proju2 (v3) = 2 0 1 − 3 3 1 1 1 + 1 2 0 1 −1 = 1 −0.5 −0.5
- 8. Gram-Schmidt Orthogonaliza- tion Process and Orthonormaliza- tion Isaac Amornortey Yowetu Orthogonalization VrsOrthonor- malization Gram-Schmidt Process Finding the orthonormal basis w1 = u1 ||u1|| = 1 √ 3 1 1 1 = 0.577 0.577 0.577 w2 = u2 ||u2|| = 1 √ 2 0 1 −1 = 0 0.707 −0.707 w3 = u3 ||u3|| = √ 6 2 0 0.5 −0.5 = 0 0.4082 −0.4082
- 9. Gram-Schmidt Orthogonaliza- tion Process and Orthonormaliza- tion Isaac Amornortey Yowetu Orthogonalization VrsOrthonor- malization Gram-Schmidt Process Example 2 Given that V is a subspace of R4 with basis 1 0 1 1 , 0 1 1 1 Find the orthogonal basis and their respective orthonormal basis of V.
- 10. Gram-Schmidt Orthogonaliza- tion Process and Orthonormaliza- tion Isaac Amornortey Yowetu Orthogonalization VrsOrthonor- malization Gram-Schmidt Process Solution u1 = v1 = 1 0 1 1 u2 = v2 − proju1 v2 = 0 1 1 1 − 2 3 1 0 1 1 = −2 3 0 1 3 1 3
- 11. Gram-Schmidt Orthogonaliza- tion Process and Orthonormaliza- tion Isaac Amornortey Yowetu Orthogonalization VrsOrthonor- malization Gram-Schmidt Process Finding the orthonormal basis w1 = u1 ||u1|| = 1 √ 3 1 0 1 1 = 0.577 0 0.577 0.577 w2 = u2 ||u2|| = √ 6 3 −2 3 0 1 3 1 3 = −0.816 0 0.408 0.408