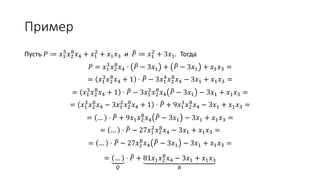Документ содержит теоретические результаты в области дискретных структур и алгебры, включая деление многочленов, теоремы Алона о нулях и аддитивную комбинаторику. Рассматриваются примеры доказательства теорем и описываются основные идеи, такие как покрытие гиперплоскостями и существование регулярных подграфов в графах. Основное внимание уделяется различным полиномам и их свойствам в контексте графов и комбинировании множеств.

1. Дискретные структуры
МФТИ, весна 2014
Александр Дайняк
www.dainiak.com

2. Одно обобщение деления многочленов
Утверждение.
Пусть 𝑃 ∈ 𝔽 𝑥1, … , 𝑥 𝑚 и 𝑃 ∈ 𝔽 𝑥𝑖 — произвольные ненулевые многочлены.
Тогда существуют 𝑄, 𝑅 ∈ 𝔽 𝑥1, … , 𝑥 𝑚 , такие, что
𝑃 = 𝑃 ⋅ 𝑄 + 𝑅,
и deg 𝑥 𝑖
𝑅 < deg 𝑥 𝑖
𝑃.
Доказательство: во всех мономах 𝑃, куда 𝑥𝑖 входит в степени больше
deg 𝑥 𝑖
𝑅, заменяем эту степень, выразив её через 𝑃.
По сути, это «деление столбиком», в котором мы рассматриваем 𝑃 как
многочлен от 𝑥𝑖 с коэффициентами из 𝔽 𝑥1, … , 𝑥𝑖−1, 𝑥𝑖+1, … , 𝑥 𝑚 .

3. Пример
Пусть 𝑃 ≔ 𝑥1
5
𝑥2
8
𝑥4 + 𝑥1
2
+ 𝑥1 𝑥3 и 𝑃 ≔ 𝑥1
2
+ 3𝑥1. Тогда
𝑃 = 𝑥1
3
𝑥2
8
𝑥4 ⋅ 𝑃 − 3𝑥1 + 𝑃 − 3𝑥1 + 𝑥1 𝑥3 =
= 𝑥1
3
𝑥2
8
𝑥4 + 1 ⋅ 𝑃 − 3𝑥1
4
𝑥2
8
𝑥4 − 3𝑥1 + 𝑥1 𝑥3 =
= 𝑥1
3
𝑥2
8
𝑥4 + 1 ⋅ 𝑃 − 3𝑥1
2
𝑥2
8
𝑥4 𝑃 − 3𝑥1 − 3𝑥1 + 𝑥1 𝑥3 =
= 𝑥1
3
𝑥2
8
𝑥4 − 3𝑥1
2
𝑥2
8
𝑥4 + 1 ⋅ 𝑃 + 9𝑥1
3
𝑥2
8
𝑥4 − 3𝑥1 + 𝑥1 𝑥3 =
= … ⋅ 𝑃 + 9𝑥1 𝑥2
8
𝑥4 𝑃 − 3𝑥1 − 3𝑥1 + 𝑥1 𝑥3 =
= … ⋅ 𝑃 − 27𝑥1
2
𝑥2
8
𝑥4 − 3𝑥1 + 𝑥1 𝑥3 =
= … ⋅ 𝑃 − 27𝑥2
8
𝑥4 𝑃 − 3𝑥1 − 3𝑥1 + 𝑥1 𝑥3 =
= …
𝑄
⋅ 𝑃 + 81𝑥1 𝑥2
8
𝑥4 − 3𝑥1 + 𝑥1 𝑥3
𝑅

4. Теорема Алона о нулях
Теорема.
Пусть 𝑃 ∈ 𝔽 𝑥1, … , 𝑥 𝑚 — произвольный полином,
и пусть 𝑥1
𝑡1
⋅ … ⋅ 𝑥 𝑚
𝑡 𝑚
— моном старшей степени, то есть 𝑖 𝑡𝑖 = deg 𝑃.
Пусть 𝑆1, … , 𝑆 𝑚 ⊆ 𝔽 — произвольные множества, такие, что 𝑆𝑖 ≥ 𝑡𝑖 + 1
для всех 𝑖.
Тогда найдутся такие 𝑠1 ∈ 𝑆1, … , 𝑠 𝑚 ∈ 𝑆 𝑚, что
𝑃 𝑠1, … , 𝑠 𝑚 ≠ 0

5. Доказательство теоремы Алона
Доказательство: индукция по deg 𝑃.
Если deg 𝑃 = 1, то 𝑃 — линейная форма:
𝑃 𝑥1, … , 𝑥 𝑚 = 𝑐0 +
𝑖
𝑐𝑖 𝑥𝑖
Если, например, 𝑐1 ≠ 0, то 𝑆1 ≥ 2 и, как бы ни были фиксированы
𝑥2 ← 𝑠2, … , 𝑥 𝑚 ← 𝑠 𝑚, уравнение 𝑃 𝑥1, 𝑠2, … , 𝑠 𝑚 = 0 имеет
не более одного корня.
Значит, найдётся 𝑠1 ∈ 𝑆1, для которого 𝑃 𝑠1, 𝑠2, … , 𝑠 𝑚 ≠ 0.

6. Доказательство теоремы Алона
Пусть deg 𝑃 > 1, и для многочленов меньшей степени утверждение
теоремы выполнено.
Б.о.о. будем считать, что 𝑡1 > 0.
Зафиксируем произвольное 𝑠 ∈ 𝑆1 и поделим с остатком 𝑃 на 𝑥1 − 𝑠 :
𝑃 = 𝑥1 − 𝑠 ⋅ 𝑄 + 𝑅,
где 𝑄 ≢ 0 и deg 𝑥1
𝑅 < deg 𝑥1
𝑥1 − 𝑠 = 1, то есть 𝑅 не зависит от 𝑥1.

7. Доказательство теоремы Алона
𝑃 = 𝑥1 − 𝑠 ⋅ 𝑄 + 𝑅,
где 𝑄 ≢ 0 и deg 𝑥1
𝑅 < deg 𝑥1
(𝑥1 − 𝑠) = 1, т.е. 𝑅 не зависит от 𝑥1.
Если найдётся набор 𝑠2 ∈ 𝑆2, … , 𝑠 𝑚 ∈ 𝑆 𝑚, такой, что 𝑅 𝑠2, … , 𝑠 𝑚 ≠ 0, то
𝑃 𝑠, 𝑠2, … , 𝑠 𝑚 ≠ 0,
что и требовалось.
Остаётся разобрать случай, когда
∀𝑠2 ∈ 𝑆2, … , ∀𝑠 𝑚 ∈ 𝑆 𝑚 𝑅 𝑠2, … , 𝑠 𝑚 = 0.

8. Доказательство теоремы Алона
𝑃 = 𝑥1 − 𝑠 ⋅ 𝑄 + 𝑅
Т.к. в 𝑃 один из мономов степени deg 𝑃 имеет вид 𝑥1
𝑡1
⋅ … ⋅ 𝑥 𝑚
𝑡 𝑚
,
то в 𝑄 один из мономов степени deg 𝑄 имеет вид 𝑥1
𝑡1−1
⋅ … ⋅ 𝑥 𝑚
𝑡 𝑚
.
По предположению индукции, найдутся такие
𝑠1 ∈ 𝑆1 ∖ 𝑠 , 𝑠2 ∈ 𝑆2, … , 𝑠 𝑚 ∈ 𝑆 𝑚,
для которых
𝑄 𝑠1, … , 𝑠 𝑚 ≠ 0.
Для таких 𝑠1, … , 𝑠 𝑚 получаем
𝑃 𝑠1, … , 𝑠 𝑚 = 𝑠1 − 𝑠 ⋅ 𝑄 𝑠1, … , 𝑠 𝑚 ≠ 0

9. Аддитивная комбинаторика
Аддитивная комбинаторика изучает свойства подмножеств
натуральных чисел и абелевых групп при сложении.
Пусть 𝐴, 𝐵 ⊆ 𝐺, где 𝐺 — абелева группа.
Обозначим
𝐴 + 𝐵 ≔ 𝑎 + 𝑏 ∣ 𝑎 ∈ 𝐴, 𝑏 ∈ 𝐵
Вопрос: как можно оценить 𝐴 + 𝐵 , если известны 𝐴 и 𝐵 ?
Пример простой оценки сверху:
𝐴 + 𝐵 ≤ min 𝐺 , 𝐴 ⋅ 𝐵

10. Теорема Коши—Давенпорта
Теорема (Cauchy, Davenport).
Если 𝐴, 𝐵 ⊆ ℤ 𝑝, где 𝑝 — простое число, то
𝐴 + 𝐵 ≥ min 𝑝, 𝐴 + 𝐵 − 1
Доказательство:
Сначала рассмотрим лёгкий случай 𝐴 + 𝐵 > 𝑝.
Для любого 𝑐 ∈ ℤ 𝑝 имеем
𝐴 + 𝑐 − 𝐵 = 𝐴 + 𝐵 > 𝑝
а значит 𝐴 ∩ 𝑐 − 𝐵 ≠ ∅, и найдутся 𝑎 ∈ 𝐴 и 𝑏 ∈ 𝐵, такие, что
𝑎 = 𝑐 − 𝑏. Отсюда 𝑐 ∈ 𝐴 + 𝐵.
Т.к. 𝑐 брался произвольным, получаем 𝐴 + 𝐵 = ℤ 𝑝.

11. Теорема Коши—Давенпорта
Пусть теперь 𝐴 + 𝐵 ≤ 𝑝.
Допустим, что 𝐴 + 𝐵 < 𝐴 + 𝐵 − 1, и придём к противоречию.
По предположению, найдётся 𝐶 ⊂ ℤ 𝑝, такое, что 𝐶 = 𝐴 + 𝐵 − 2
и 𝐴 + 𝐵 ⊆ 𝐶.
Рассмотрим многочлен
𝑃 𝑥, 𝑦 ≔
𝑐∈𝐶
𝑥 + 𝑦 − 𝑐 ∈ ℤ 𝑝 𝑥, 𝑦
Заметим, что 𝑃 𝑥, 𝑦 = 0 для любых 𝑥 ∈ 𝐴, 𝑦 ∈ 𝐵.

12. Теорема Коши—Давенпорта
𝑃 𝑥, 𝑦 ≔
𝑐∈𝐶
𝑥 + 𝑦 − 𝑐 ∈ ℤ 𝑝 𝑥, 𝑦
Раскрыв скобки в определении 𝑃, видим, что
coef 𝑥 𝐴 −1 𝑦 𝐵 −1 𝑃 = 𝐴 + 𝐵 −2 !
𝐴 −1 ! 𝐵 −1 !
mod 𝑝 ≠ 0
то есть моном 𝑥 𝐴 −1 𝑦 𝐵 −1 реально входит в многочлен.
По теореме Алона, найдутся 𝑎 ∈ 𝐴 и 𝑏 ∈ 𝐵, такие, что 𝑃 𝑎, 𝑏 ≠ 0.
Но такого не может быть по определению 𝑃.

13. Покрытие вершин куба гиперплоскостями
Вопрос: сколько плоскостей нужно, чтобы покрыть все, кроме
одной, вершины куба?
Теорема (Алон, Фюреди).
Наименьшее число плоскостей, достаточное, чтобы покрыть все,
кроме одной, вершины куба в ℝ 𝑛, равно 𝑛.
Доказательство:
Б.о.о. будем считать, что у нас куб 0,1 𝑛, и что вершина, которую
мы не покрываем 0,0, … , 0 .

14. Покрытие вершин куба гиперплоскостями
Куб 0,1 𝑛, не покрываем вершину 0,0, … , 0 .
𝑛 плоскостей достаточно — например, такие:
• 𝑥1 − 1 = 0
• 𝑥2 − 1 = 0
• …
• 𝑥 𝑛 − 1 = 0
Сложная часть — доказать, что меньшим числом плоскостей
не обойтись.
Докажем это от противного…

15. Покрытие вершин куба гиперплоскостями
Допустим, мы обошлись 𝑚 плоскостями, 𝑚 < 𝑛. Пусть их уравнения такие:
𝒂1, 𝒙 − 𝑏1 = 0
⋮
𝒂 𝑚, 𝒙 − 𝑏 𝑚 = 0
При этом 𝑏1, … , 𝑏 𝑚 ≠ 0, т.к. ни одна из плоскостей не должна покрывать точку 0,0, … , 0 .
Рассмотрим многочлен:
𝑃 𝑥1, … , 𝑥 𝑛 ≔
𝑗=1
𝑚
𝑏𝑗 − 𝒂𝑗, 𝒙 −
𝑗=1
𝑚
𝑏𝑗 ⋅
𝑖=1
𝑛
1 − 𝑥𝑖
Имеем deg 𝑃 = 𝑛, и
coef 𝑥1⋅𝑥2⋅…⋅𝑥 𝑛
𝑃 = −1 𝑛+1
𝑗=1
𝑚
𝑏𝑗 ≠ 0.
По теореме Алона, найдутся 𝛼1 ∈ 0,1 , … , 𝛼 𝑛 ∈ 0,1 , для которых 𝑃 𝛼1, … , 𝛼 𝑛 ≠ 0.

16. Покрытие вершин куба гиперплоскостями
Допустим, мы обошлись 𝑚 плоскостями:
𝒂1, 𝒙 − 𝑏1 = 0
⋮
𝒂 𝑚, 𝒙 − 𝑏 𝑚 = 0
По теореме Алона, найдётся точка из 0,1 𝑛, на которой многочлен
𝑃 𝑥1, … , 𝑥 𝑛 ≔ 𝑗=1
𝑚
𝑏𝑗 − 𝒂𝑗, 𝒙 − 𝑗=1
𝑚
𝑏𝑗 ⋅ 𝑖=1
𝑛
1 − 𝑥𝑖
не равен нулю. Но это невозможно:
• 𝑃 0, … , 0 = 𝑗=1
𝑚
𝑏𝑗 − 𝑗=1
𝑚
𝑏𝑗 ⋅ 𝑖=1
𝑛
1 = 0
• Для любой точки 𝛼1, … , 𝛼 𝑛 ∈ 0,1 𝑛
∖ 0, … , 0 имеем
𝑃 𝛼1, … , 𝛼 𝑛 = 𝑗=1
𝑚
0 − 𝑗=1
𝑚
𝑏𝑗 ⋅ 0 = 0

17. Регулярные подграфы в регулярных графах
Общая постановка многих задач в теории графов:
в данном графе с известными свойствами выделить подграф
с требуемыми свойствами.
Например:
• В заданном графе найти максимальную клику
• В заданном несвязном графе найти компоненту связности с
максимальным числом вершин.
• …

18. Регулярные подграфы в регулярных графах
Вопрос: во всяком ли 𝑘-регулярном графе существует
𝑘 − 1 -регулярный подграф?
Известно следующее:
• Это так для 𝑘 ≤ 3 — простое упражнение.
• Это так для 𝑘 = 4 — и это трудная теорема (В.А. Ташкинов ’1984)
• Это в общем случае не верно для 𝑘 ≥ 6

19. Регулярные подграфы в регулярных графах
Вопрос: во всяком ли 𝑘-регулярном графе существует
𝑘′-регулярный подграф (𝑘′ < 𝑘)?
Известно, например, что для любых нечётных 𝑘 и 𝑘′
ответ на вопрос положительный.
Если ослабить условие «строгой» регулярности и рассматривать
«почти регулярные» графы (у которых степени вершин близки,
но необязательно равны) — тоже можно доказать кое-что
интересное…

20. Регулярные подграфы в регулярных графах
Теорема (Алон, Фридланд, Калаи).
Пусть 𝑝 — простое число. Пусть 𝐺 = 𝑉, 𝐸 — мультиграф
(без петель), удовлетворяющий условиям
• Δ 𝐺 ≤ 2𝑝 − 1,
• 1
𝑉 𝑣∈𝑉 𝑑 𝑣 > 2𝑝 − 2.
Тогда в 𝐺 есть 𝑝-регулярный подграф.

21. Доказательство теоремы А—Ф—К
• Δ 𝐺 ≤ 2𝑝 − 1, и 1
𝑉 𝑣∈𝑉 𝑑 𝑣 > 2𝑝 − 2
Для каждого 𝑣 ∈ 𝑉 и 𝑒 ∈ 𝐸 положим
𝟙 𝑣,𝑒 ≔
1, если 𝑣 и 𝑒 инцидентны
0, иначе
Каждому 𝑒 ∈ 𝐸 сопоставим переменную 𝑥 𝑒.
Рассмотрим многочлен от переменных 𝑥 𝑒 𝑒∈𝐸 с коэффициентами в ℤ 𝑝:
𝑃 ≔
𝑣∈𝑉
1 −
𝑒∈𝐸
𝟙 𝑣,𝑒 𝑥 𝑒
𝑝−1
−
𝑒∈𝐸
1 − 𝑥 𝑒

22. Доказательство теоремы А—Ф—К
• 1
𝑉 𝑣∈𝑉 𝑑 𝑣 > 2𝑝 − 2
𝑃 ≔
𝑣∈𝑉
1 −
𝑒∈𝐸
𝟙 𝑣,𝑒 𝑥 𝑒
𝑝−1
𝑄
−
𝑒∈𝐸
1 − 𝑥 𝑒
Из условия, 2 ⋅ 𝐸 = 𝑣∈𝑉 𝑑 𝑣 > 2𝑝 − 2 ⋅ 𝑉 , отсюда
deg 𝑄 ≤ 𝑝 − 1 ⋅ 𝑉 < 𝐸 .
Следовательно, deg 𝑃 = 𝐸 .
При этом, coef 𝑒∈𝐸 𝑥 𝑒
𝑃 = −1 𝐸 +1
≠ 0.

23. Доказательство теоремы А—Ф—К
𝑃 ≔
𝑣∈𝑉
1 −
𝑒∈𝐸
𝟙 𝑣,𝑒 𝑥 𝑒
𝑝−1
−
𝑒∈𝐸
1 − 𝑥 𝑒
deg 𝑃 = 𝐸 и coef 𝑒∈𝐸 𝑥 𝑒
𝑃 = −1 𝐸 +1
≠ 0.
Значит, по теореме Алона, найдётся набор значений 𝜶 = 𝛼 𝑒 𝑒∈𝐸 ∈ 0,1 𝐸
, такой,
что 𝑃 𝜶 ≠ 0.
При этом для любого 𝑣 ∈ 𝑉 имеем
𝑒∈𝐸
𝟙 𝑣,𝑒 𝛼 𝑒 =
𝑝
0,
иначе, по м. т. Ферма, получилось бы 𝑒∈𝐸 𝟙 𝑣,𝑒 𝛼 𝑒
𝑝−1
=
𝑝
1 ⇒ 𝑃 𝜶 = 0 (в ℤ 𝑝).

24. Доказательство теоремы А—Ф—К
• Δ 𝐺 ≤ 2𝑝 − 1
• 𝑃 ≔ 𝑣∈𝑉 1 − 𝑒∈𝐸 𝟙 𝑣,𝑒 𝑥 𝑒
𝑝−1
− 𝑒∈𝐸 1 − 𝑥 𝑒
Нашли 𝜶 ∈ 0,1 𝐸
, т. ч. 𝑃 𝜶 ≠ 0, и ∀𝑣 ∈ 𝑉
𝑒∈𝐸
𝟙 𝑣,𝑒 𝛼 𝑒 =
𝑝
0
Кроме того, видно, что 𝜶 ≠ 𝟎. Взяв те рёбра 𝐺, для которых 𝛼 𝑒 = 1,
и все вершины 𝐺, получим непустой остовный подграф 𝐺′.
В подграфе 𝐺′ степень каждой вершины 𝑣 равна 𝑒∈𝐸 𝟙 𝑣,𝑒 𝛼 𝑒 =
𝑝
0,
а значит, эта степень равна нулю либо 𝑝.

25. Доказательство теоремы А—Ф—К
По набору 𝜶 построили непустой остовный подграф 𝐺′.
В подграфе 𝐺′ степень каждой вершины равна нулю или 𝑝.
Выбросив из 𝐺′ вершины нулевой степени, получим искомый
𝑝-регулярный подграф.