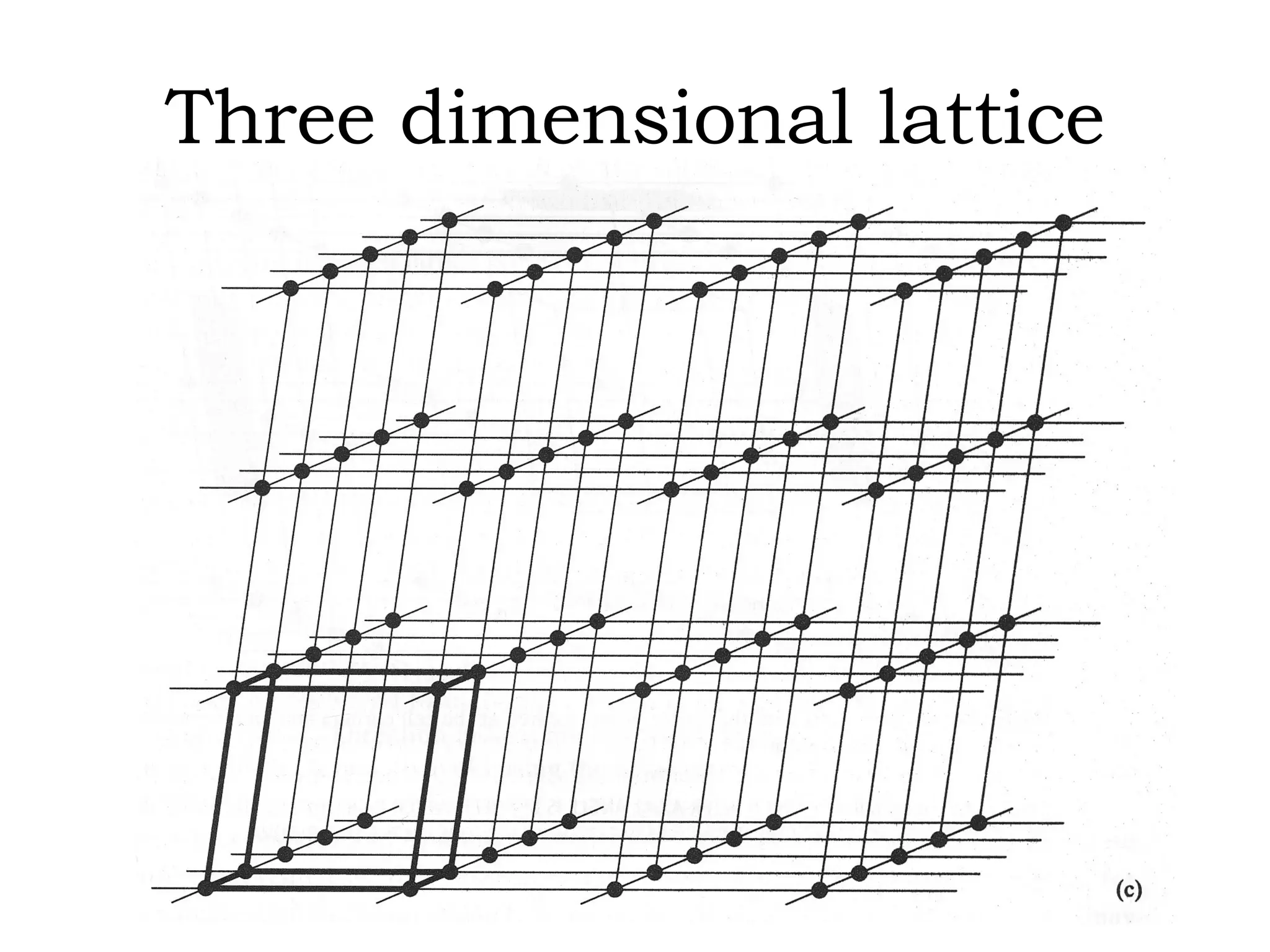
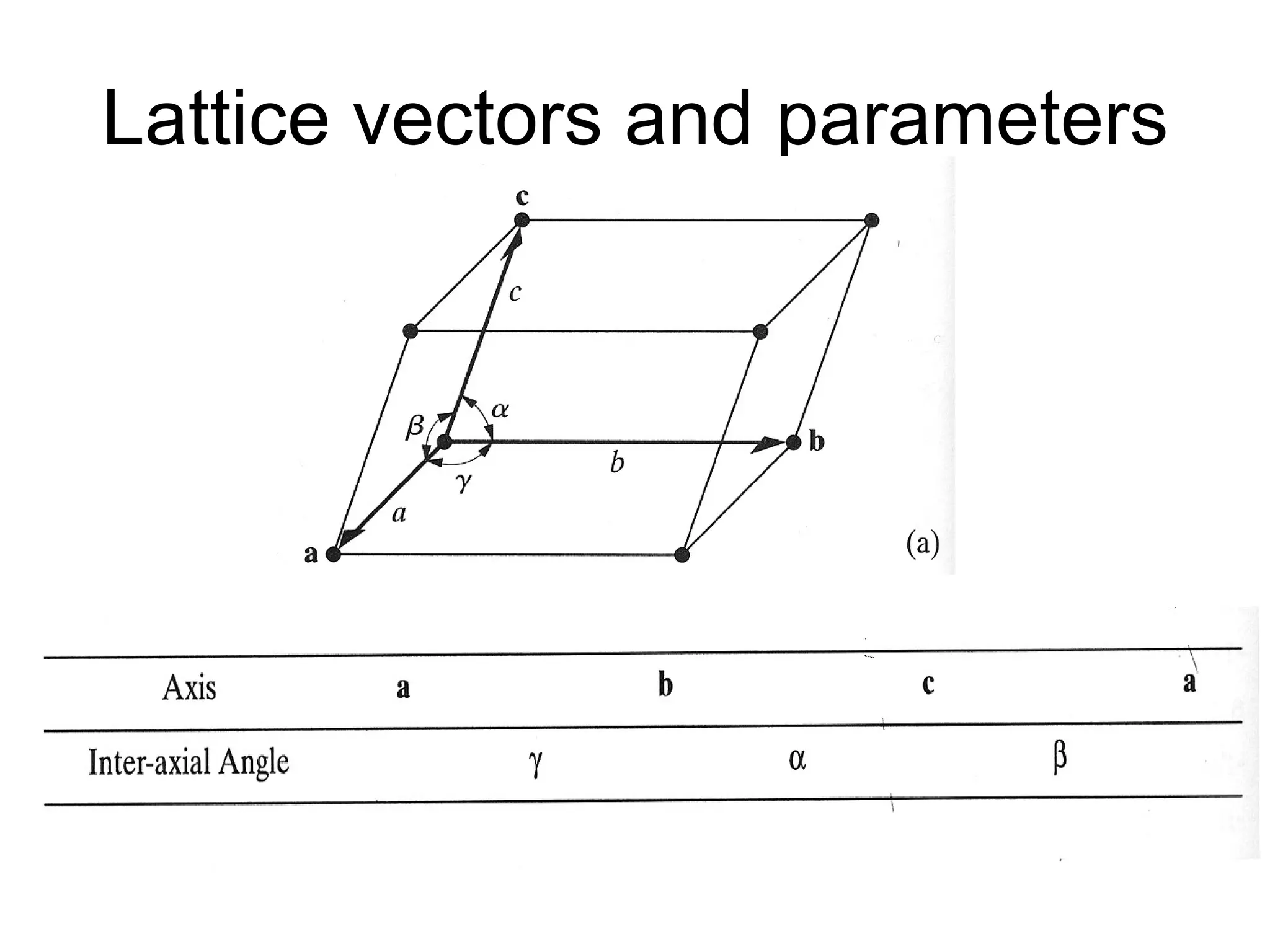
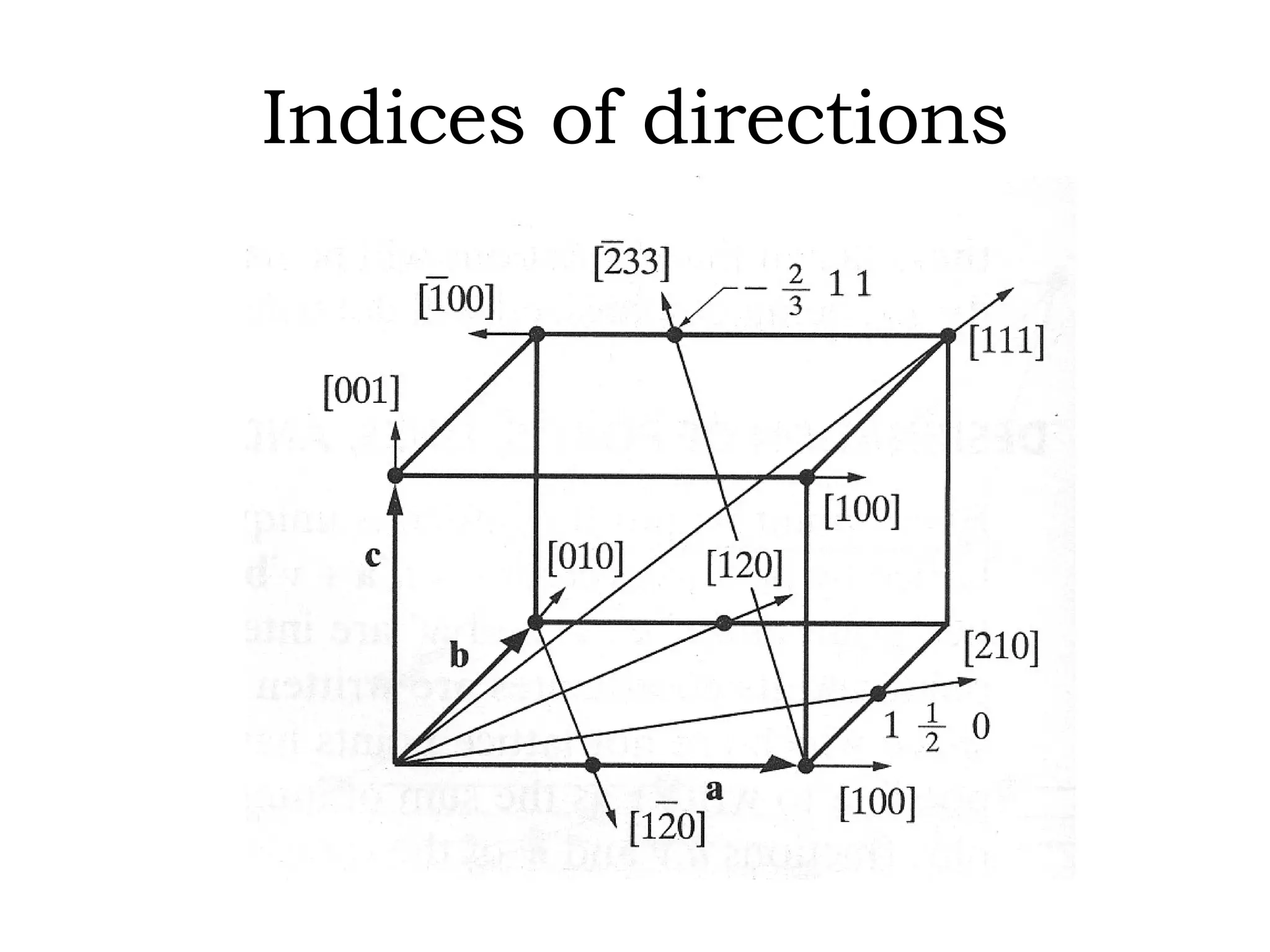
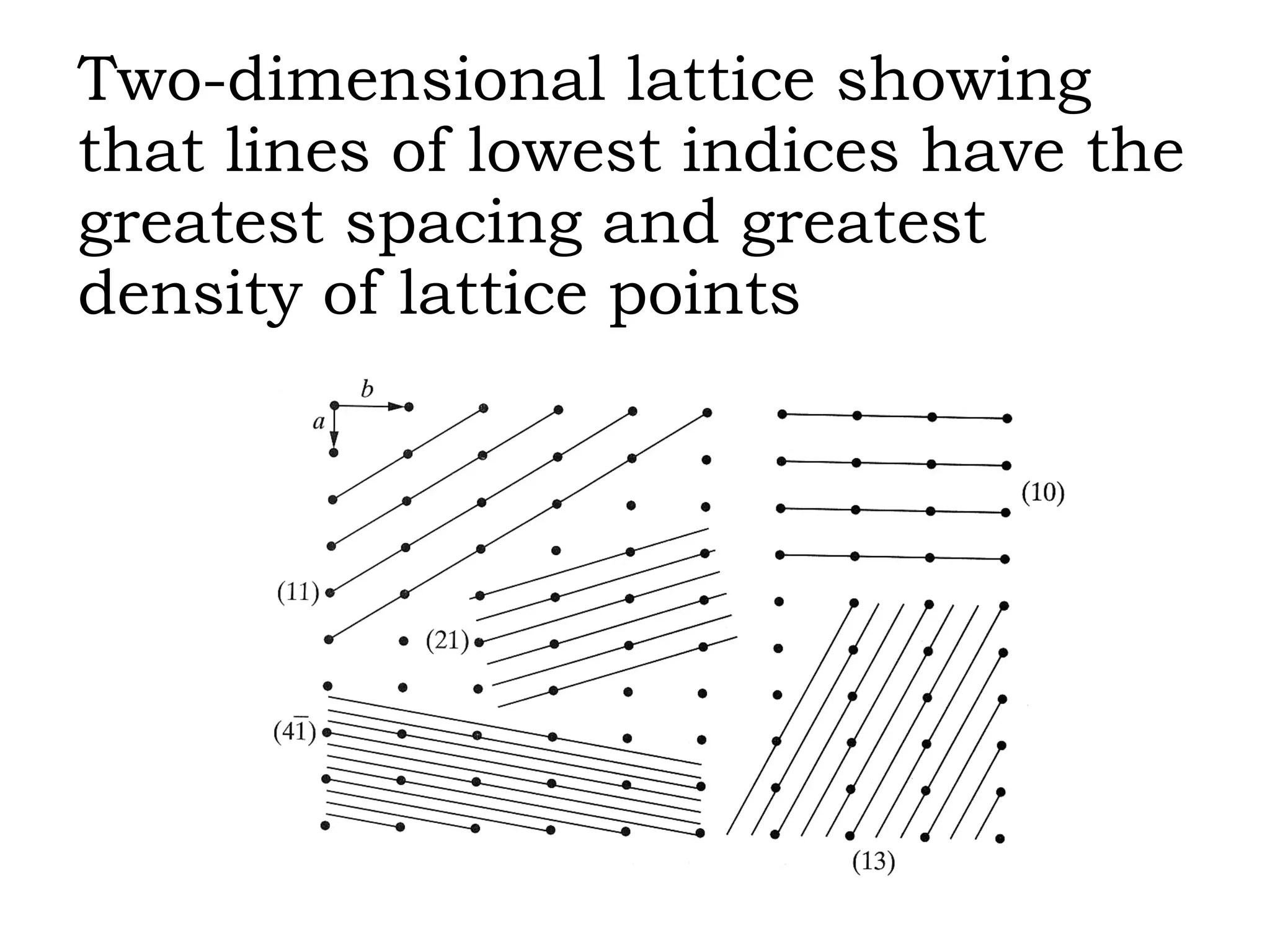
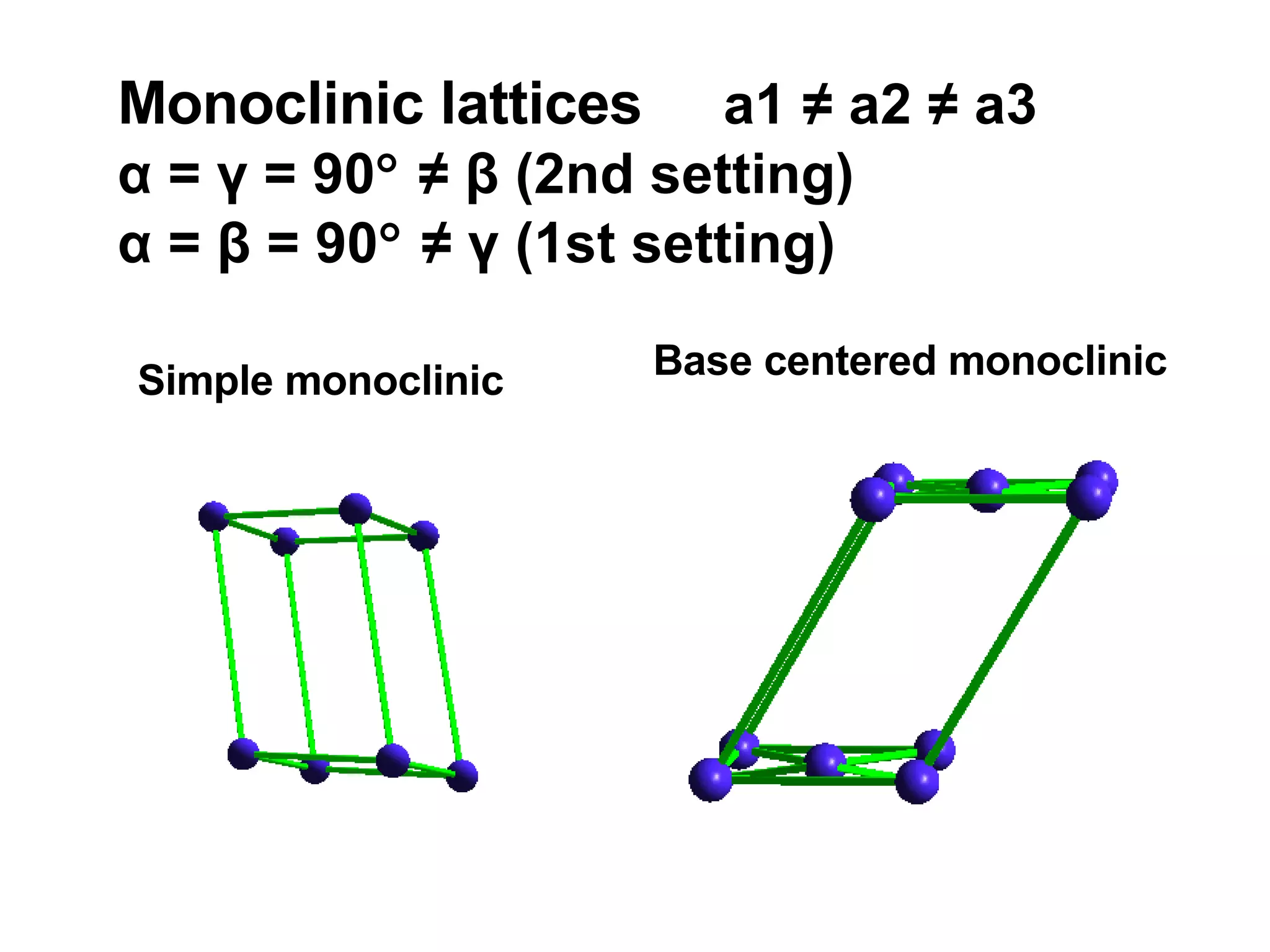
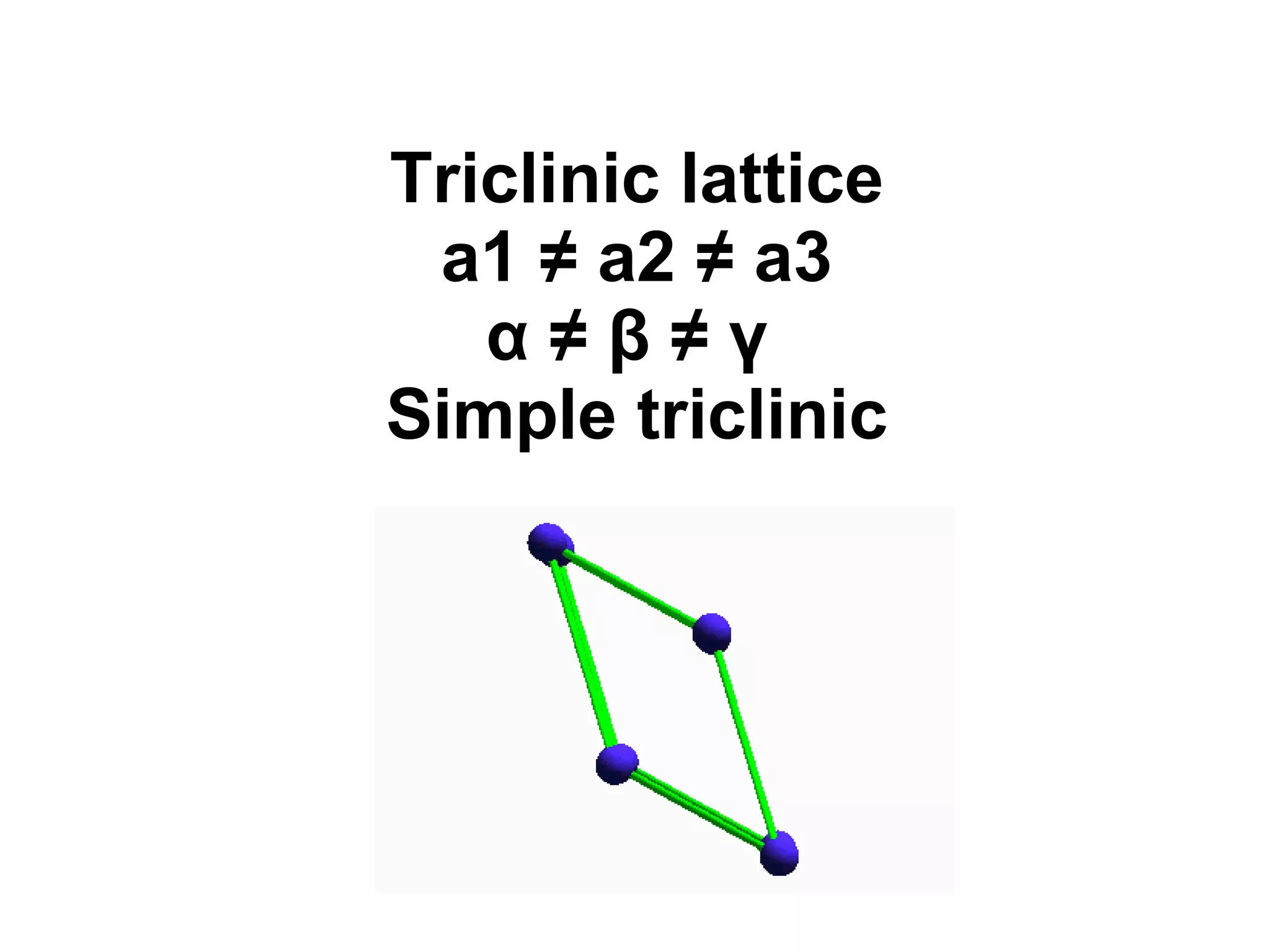
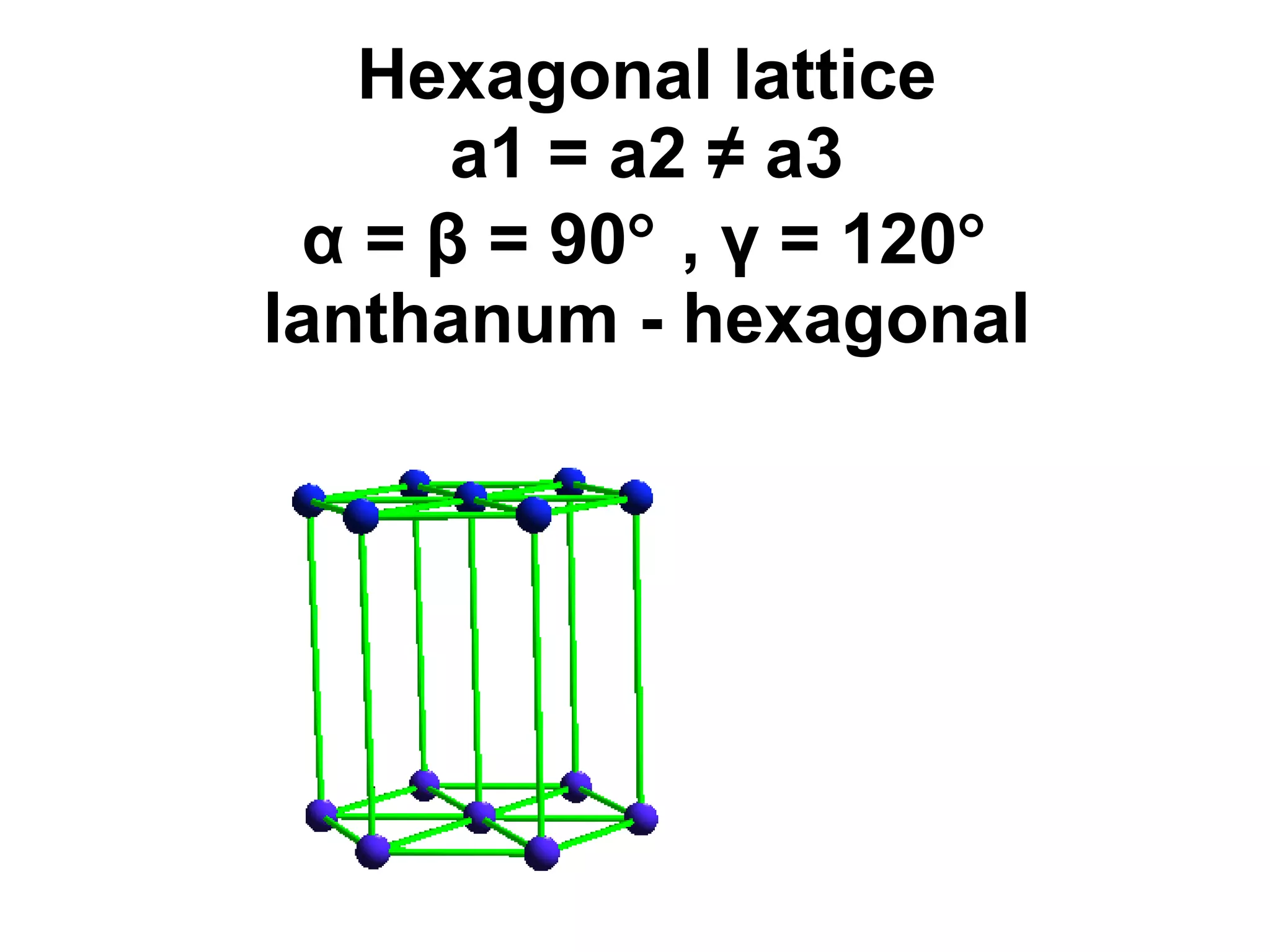
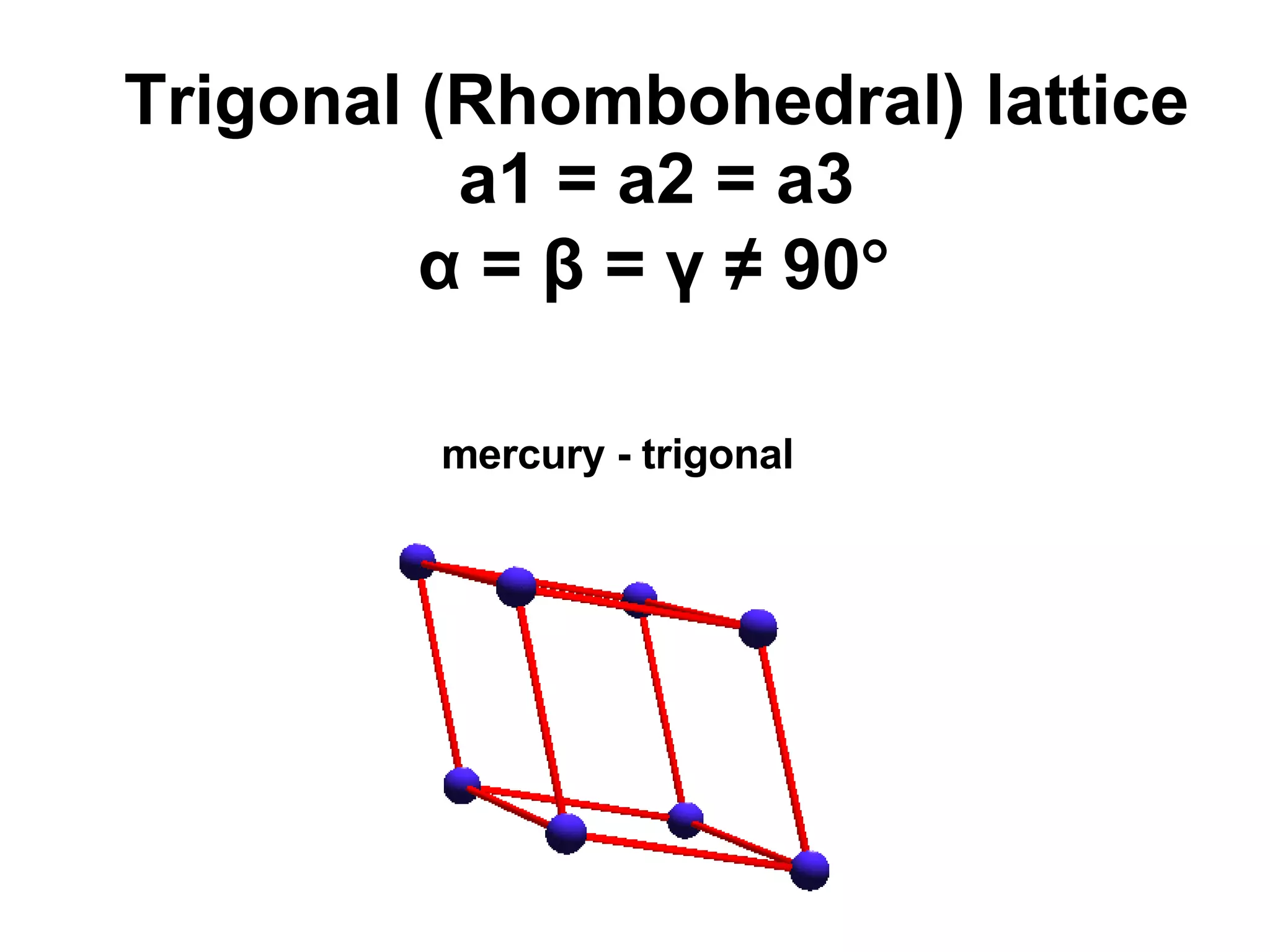
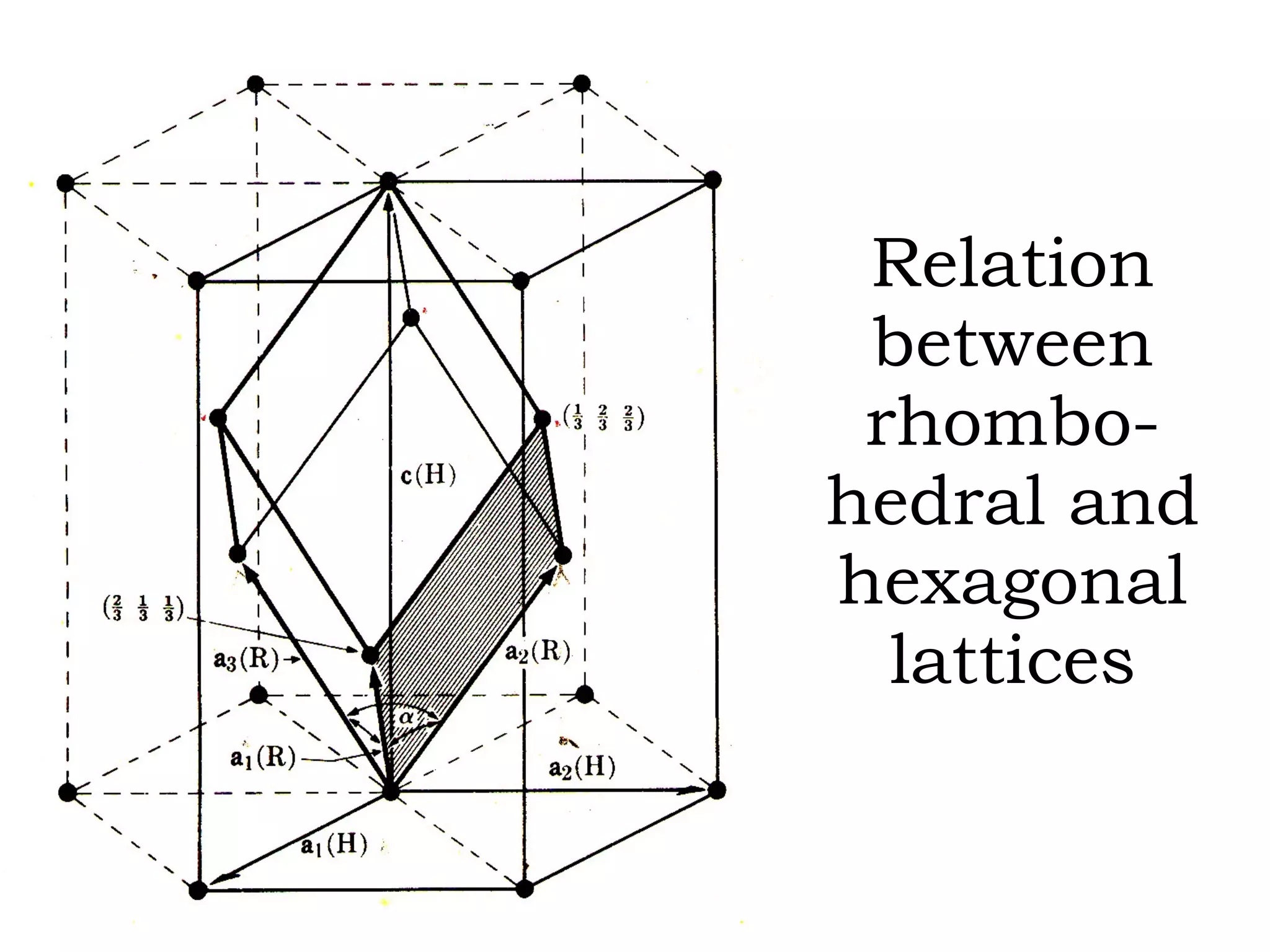
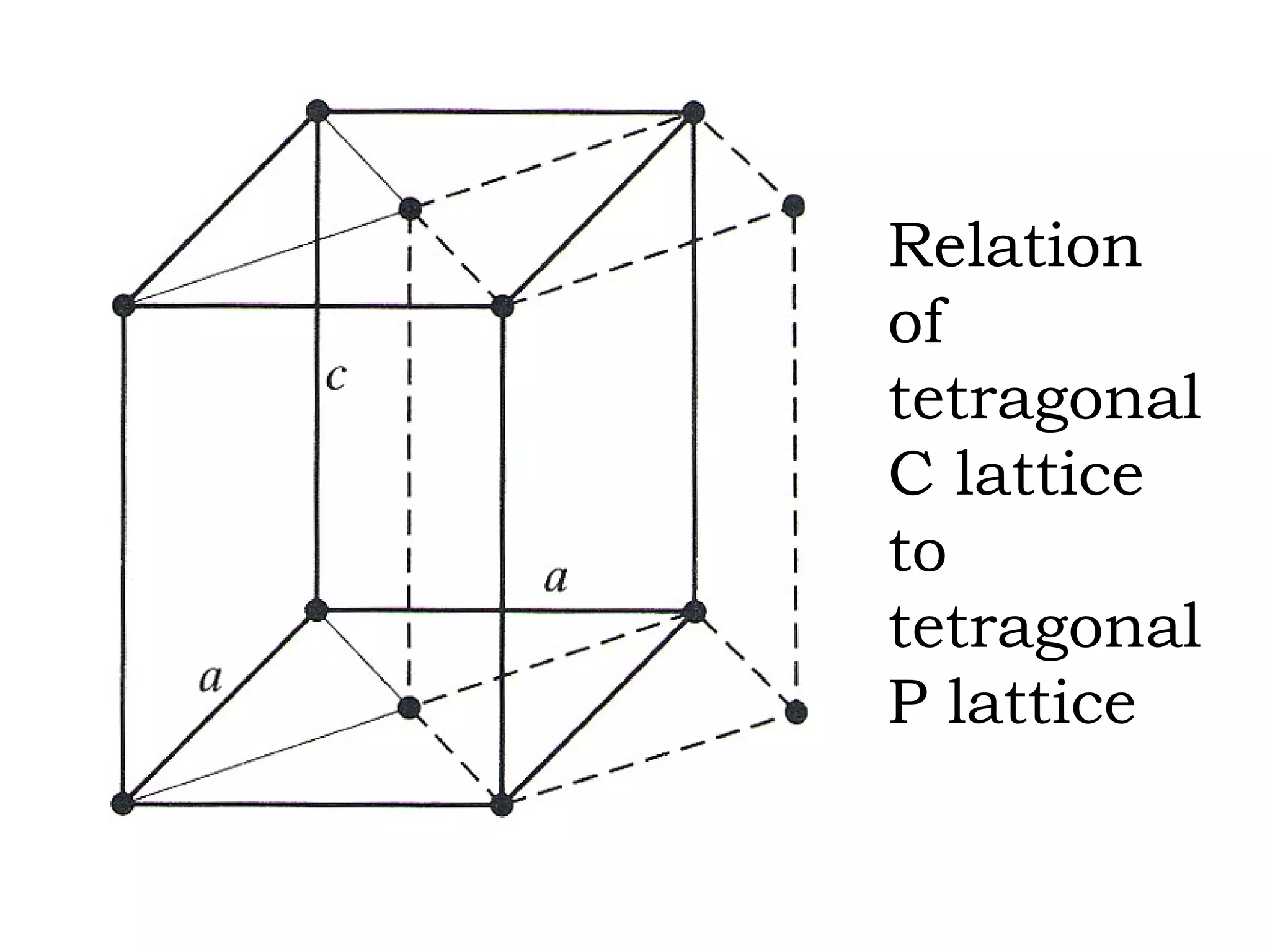
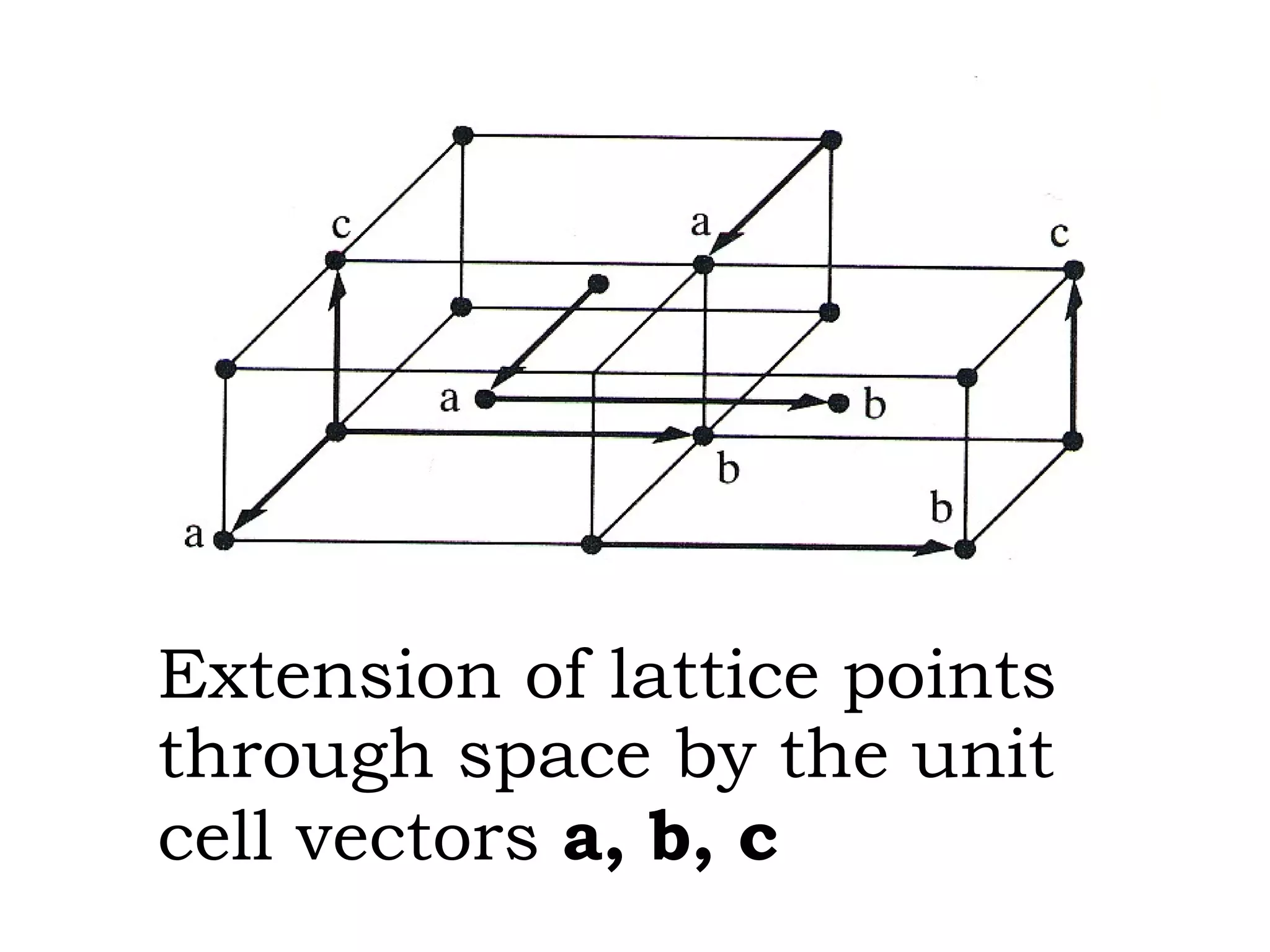
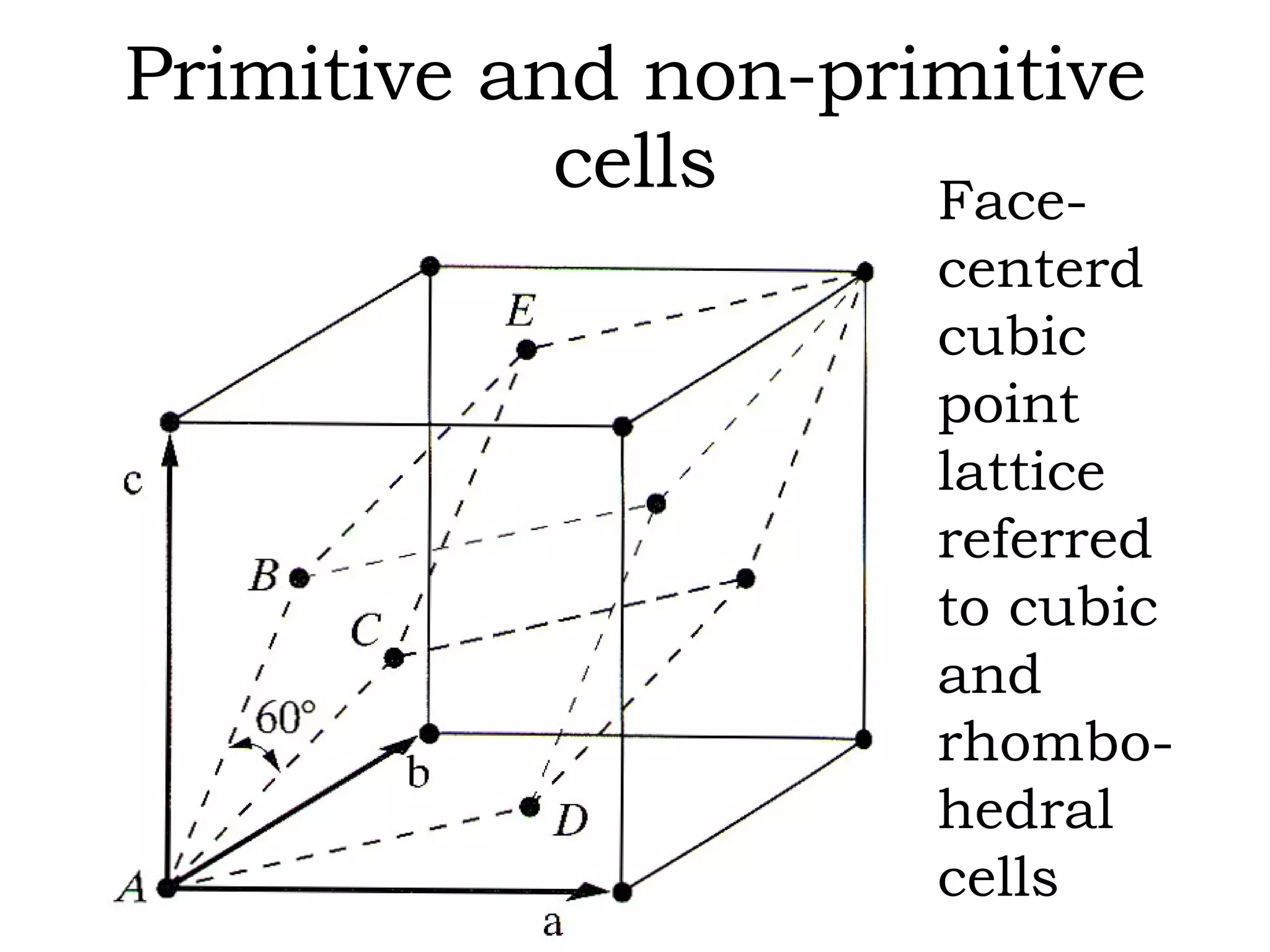
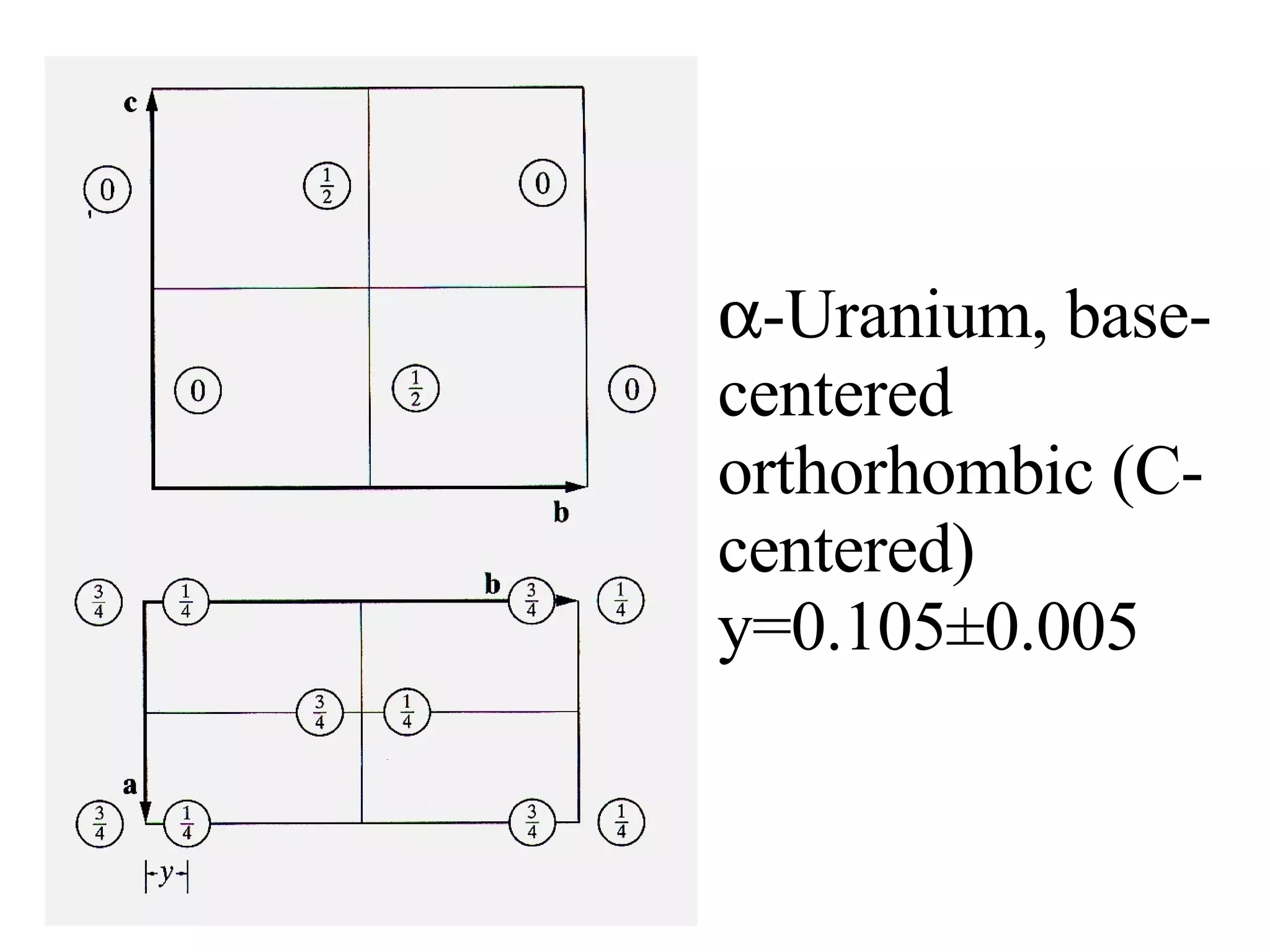
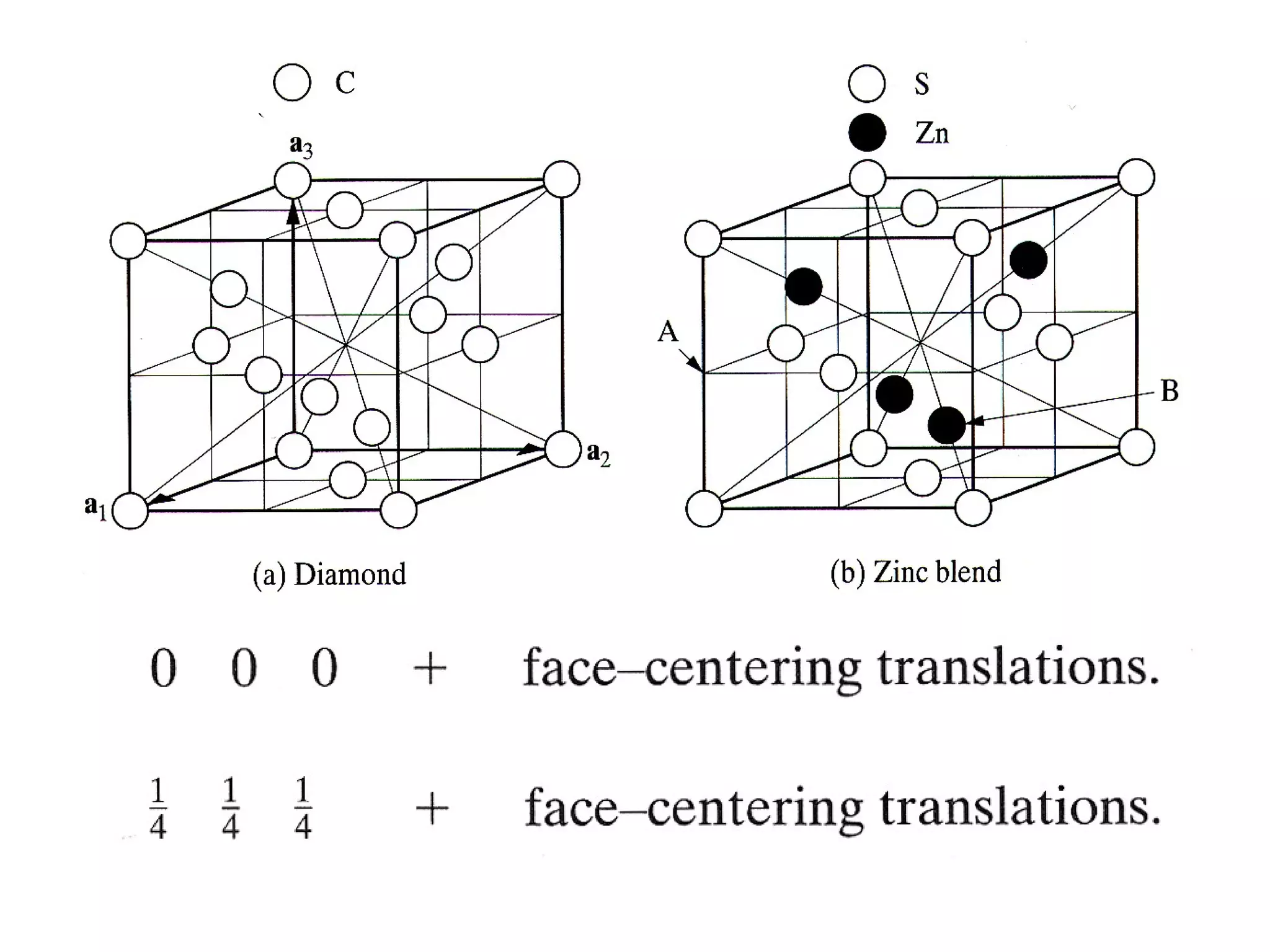
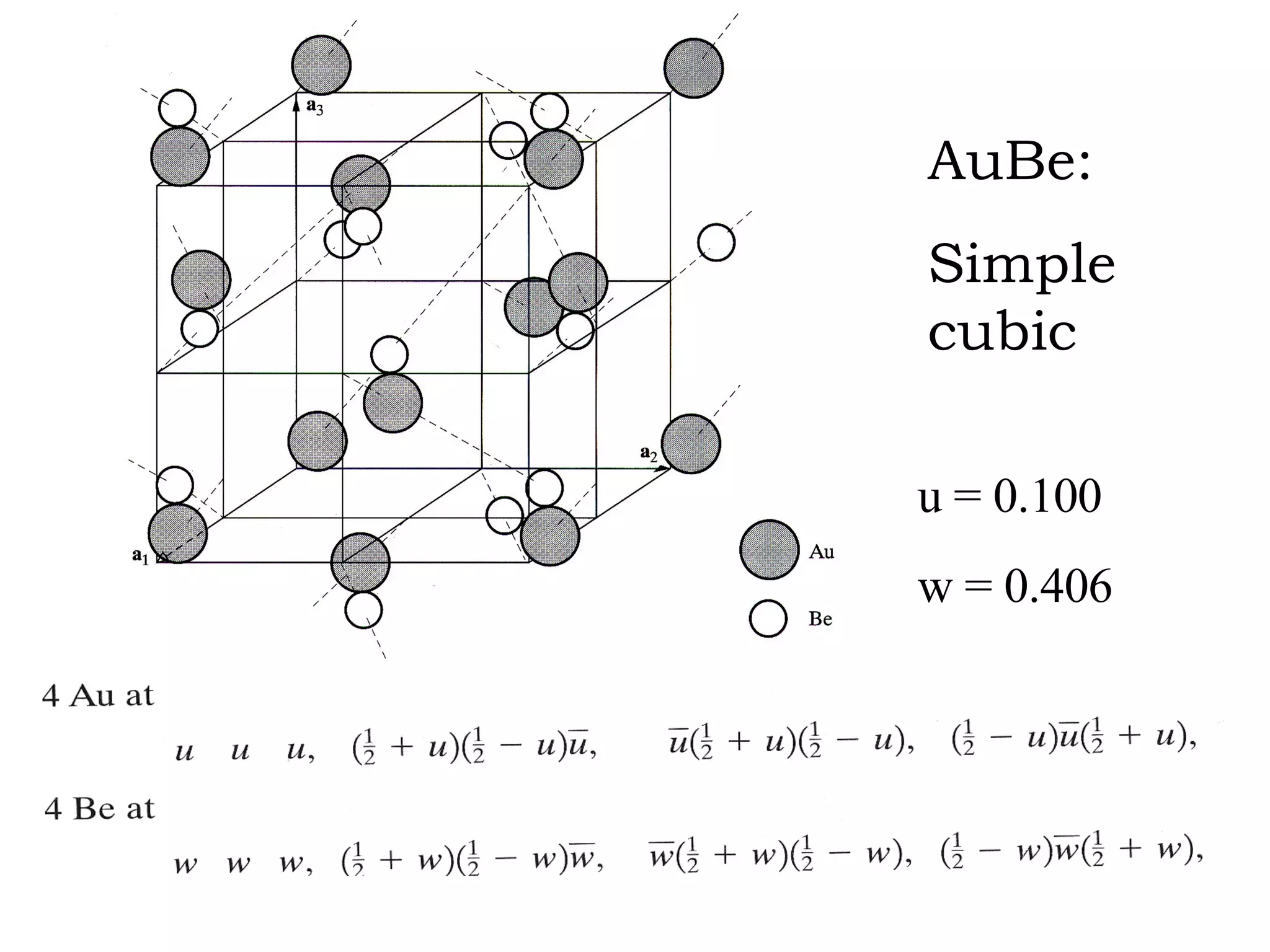
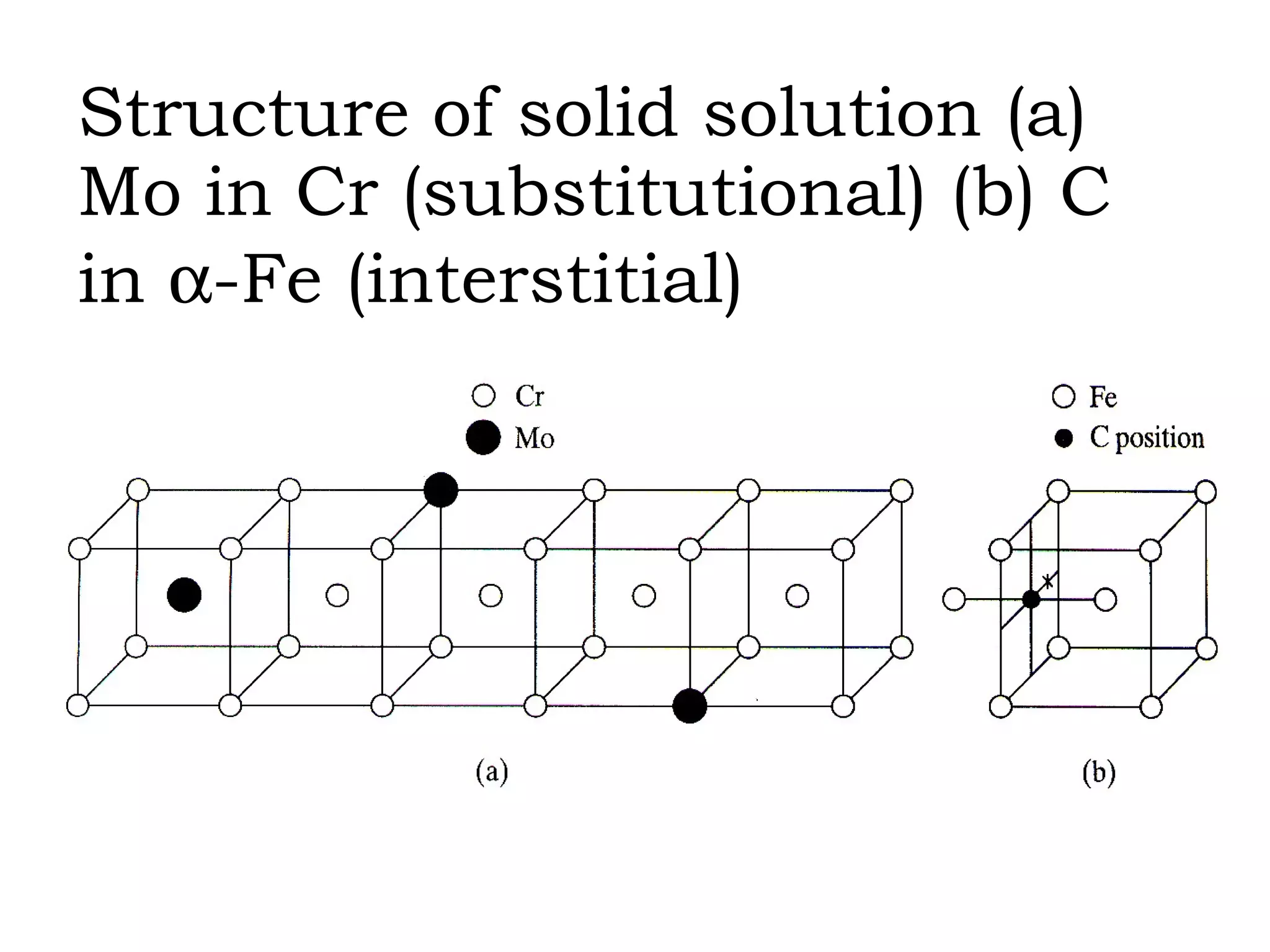
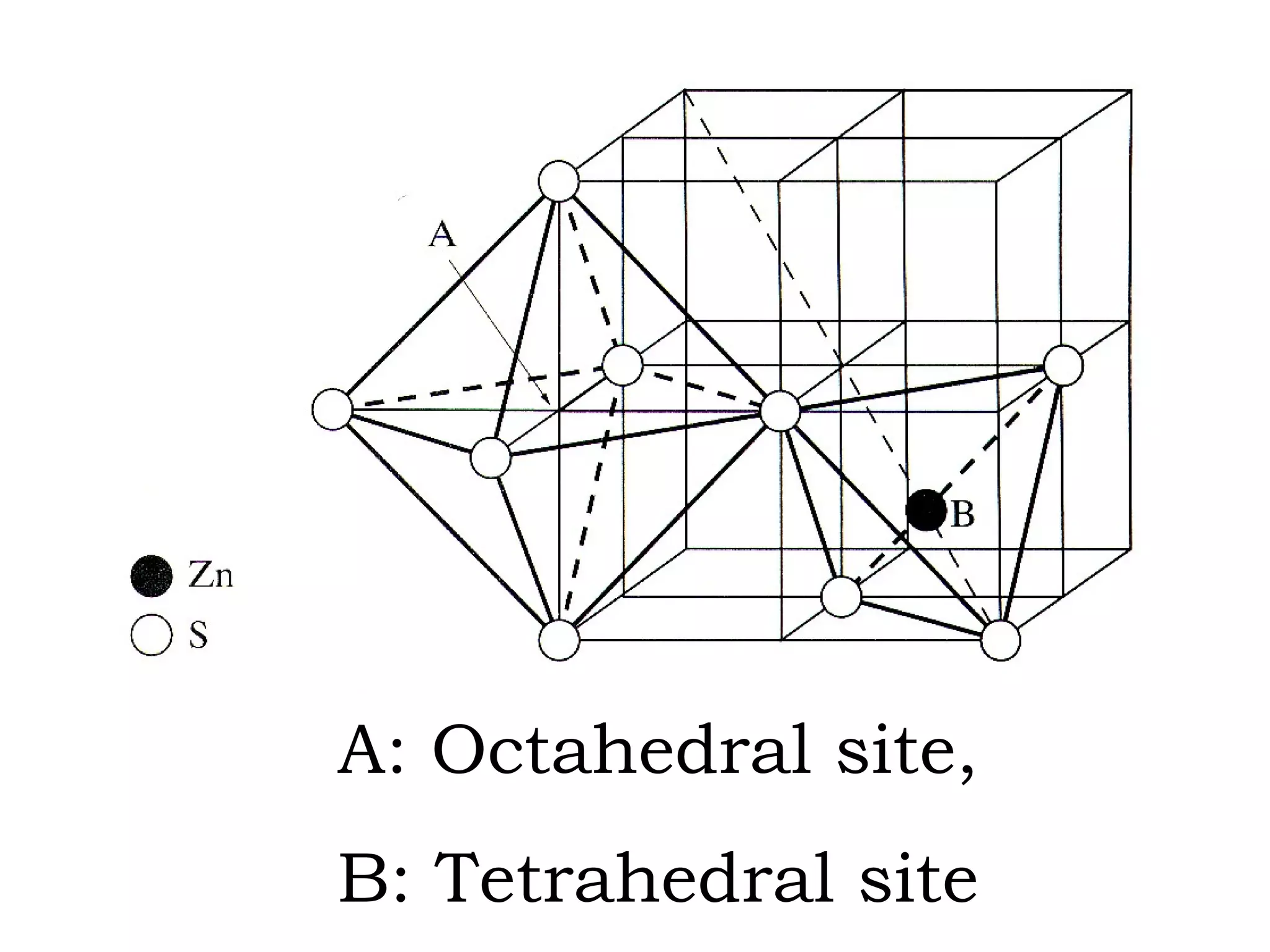
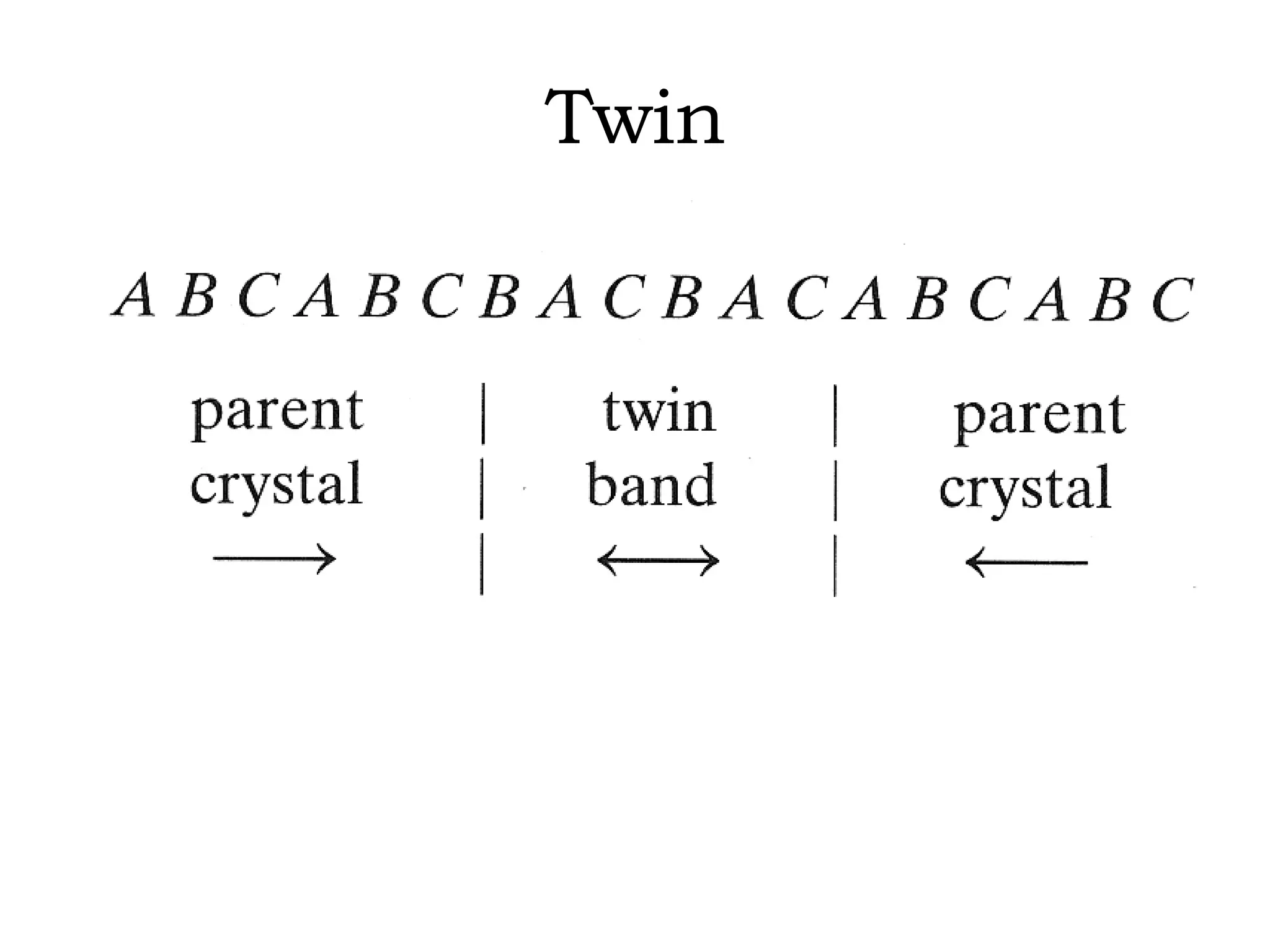
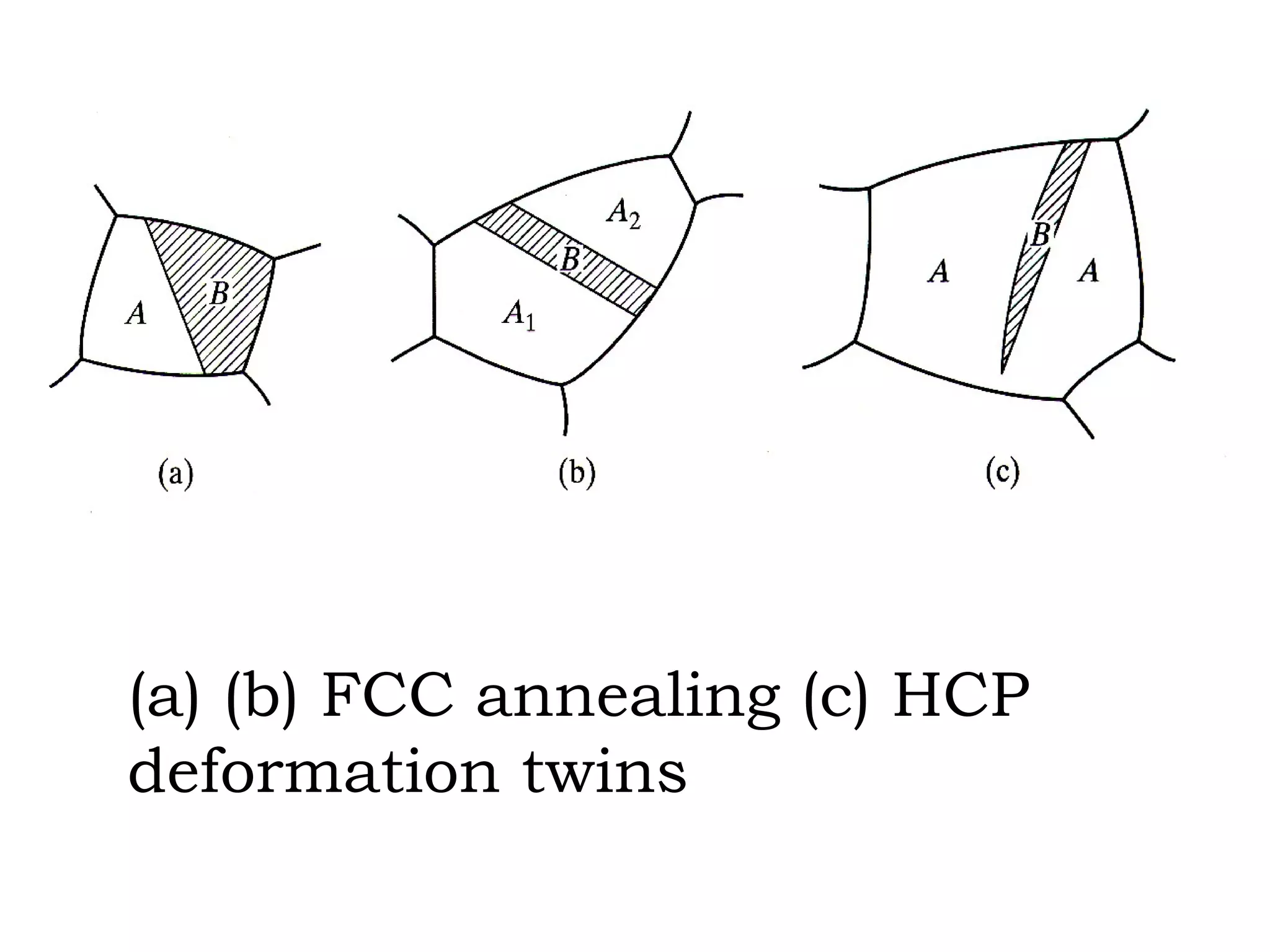
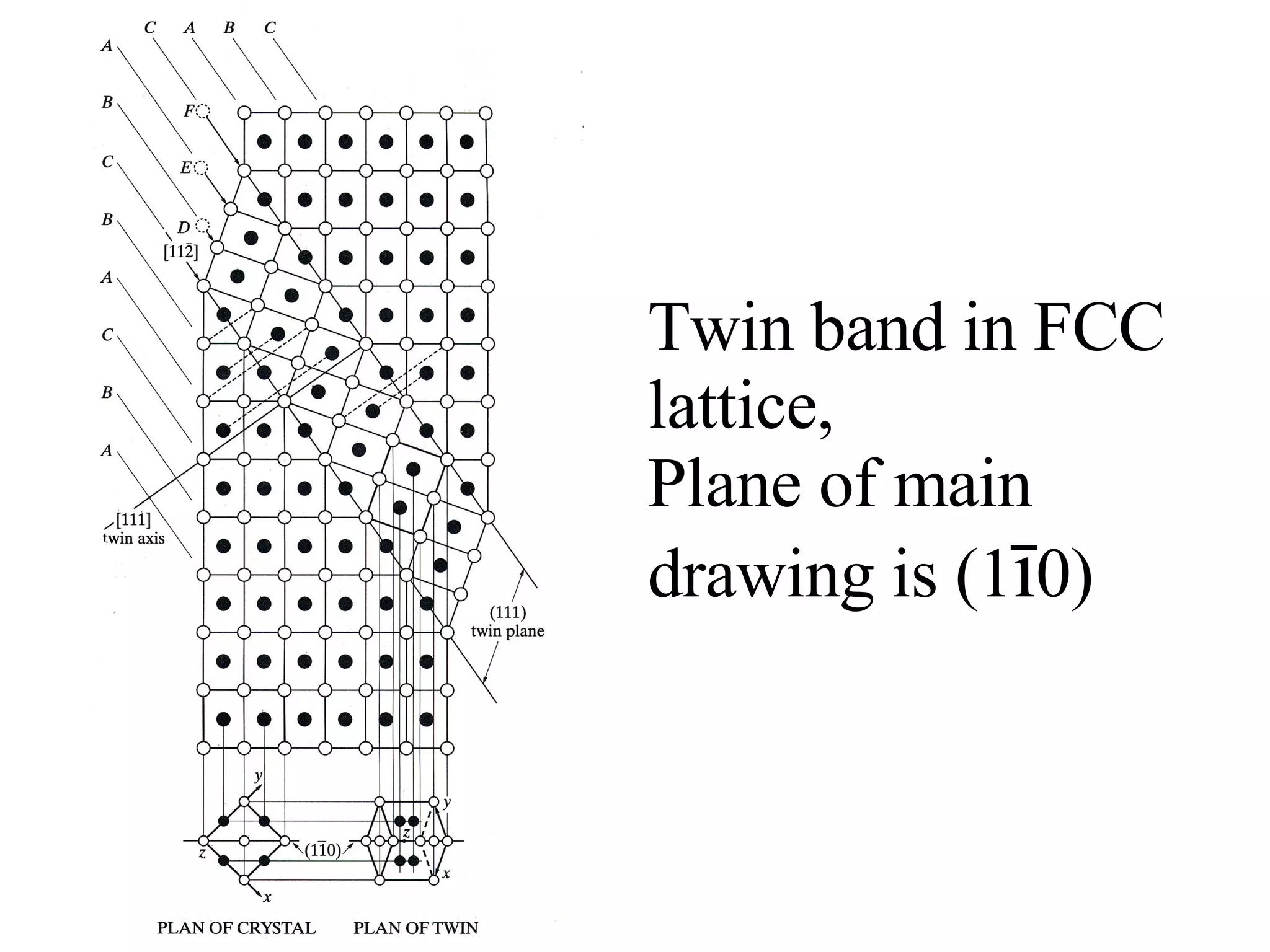
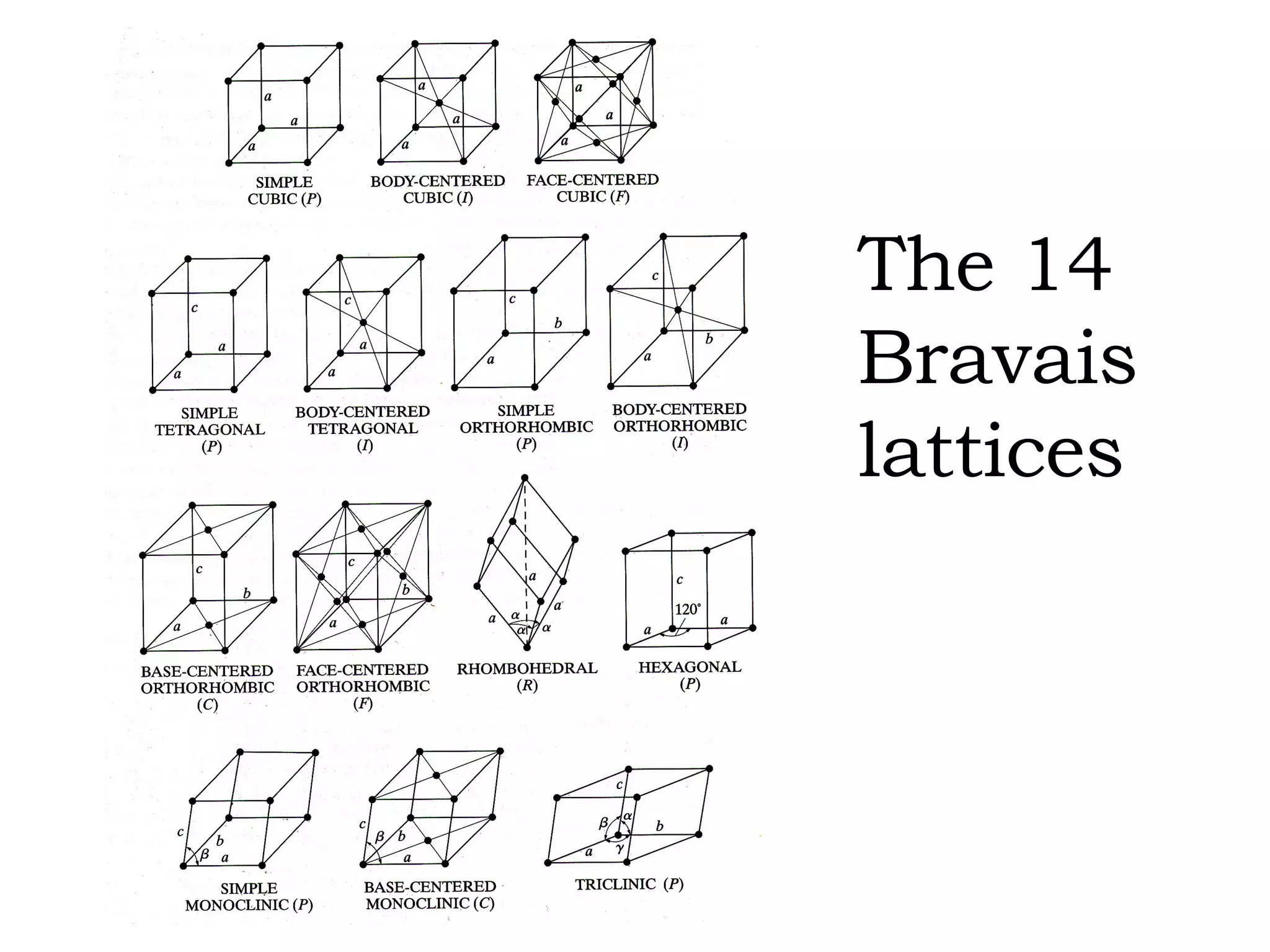
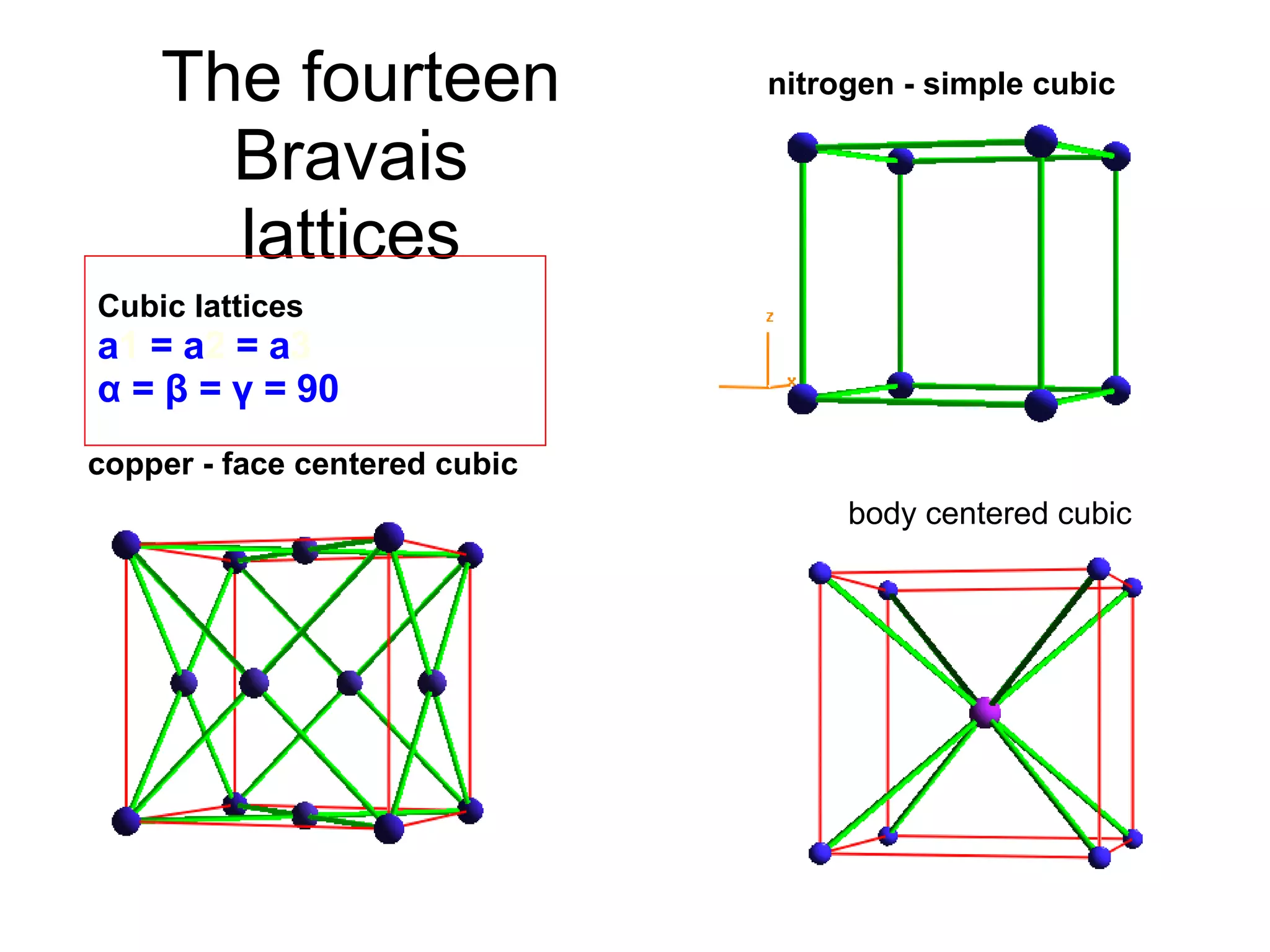
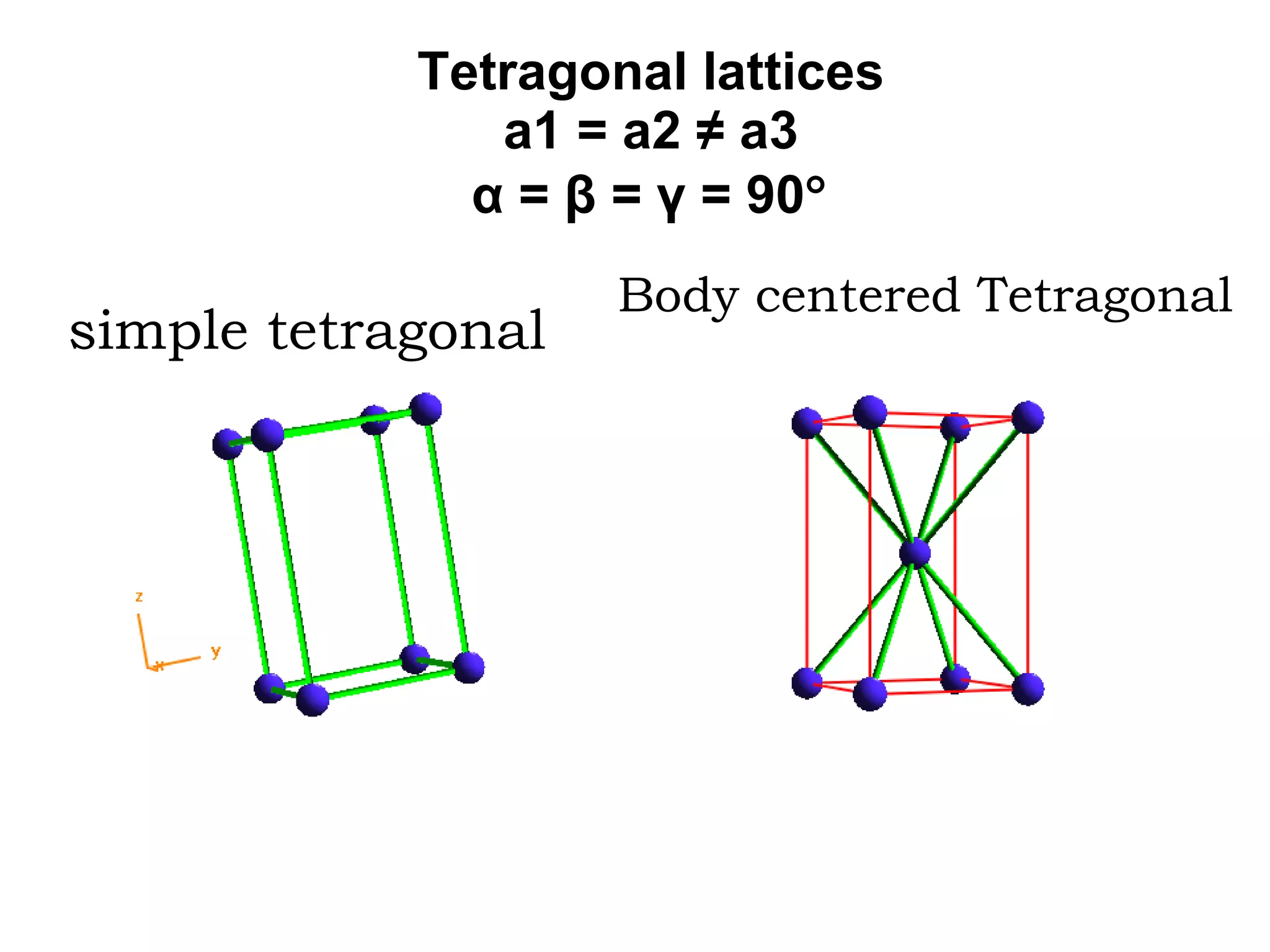
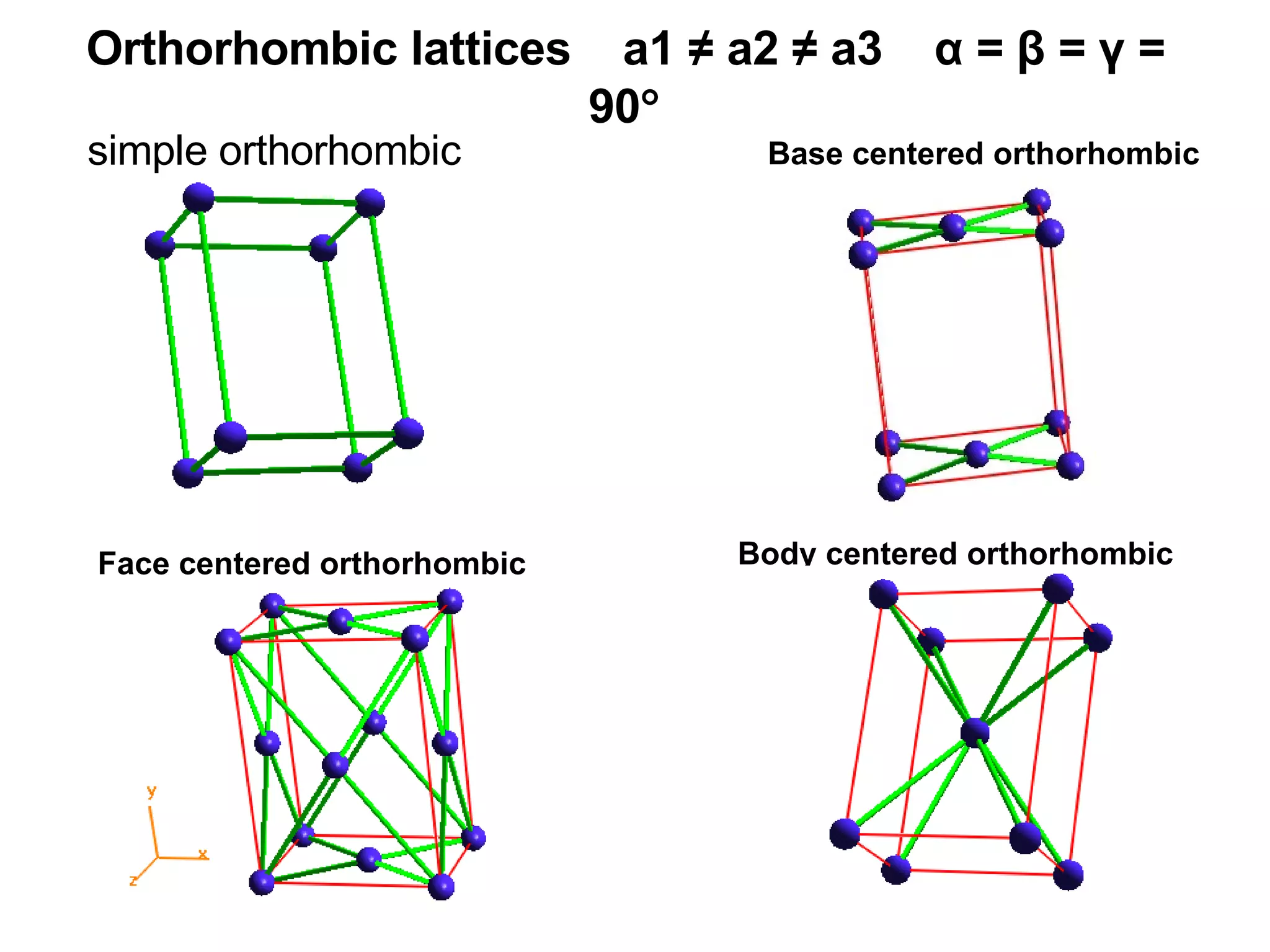
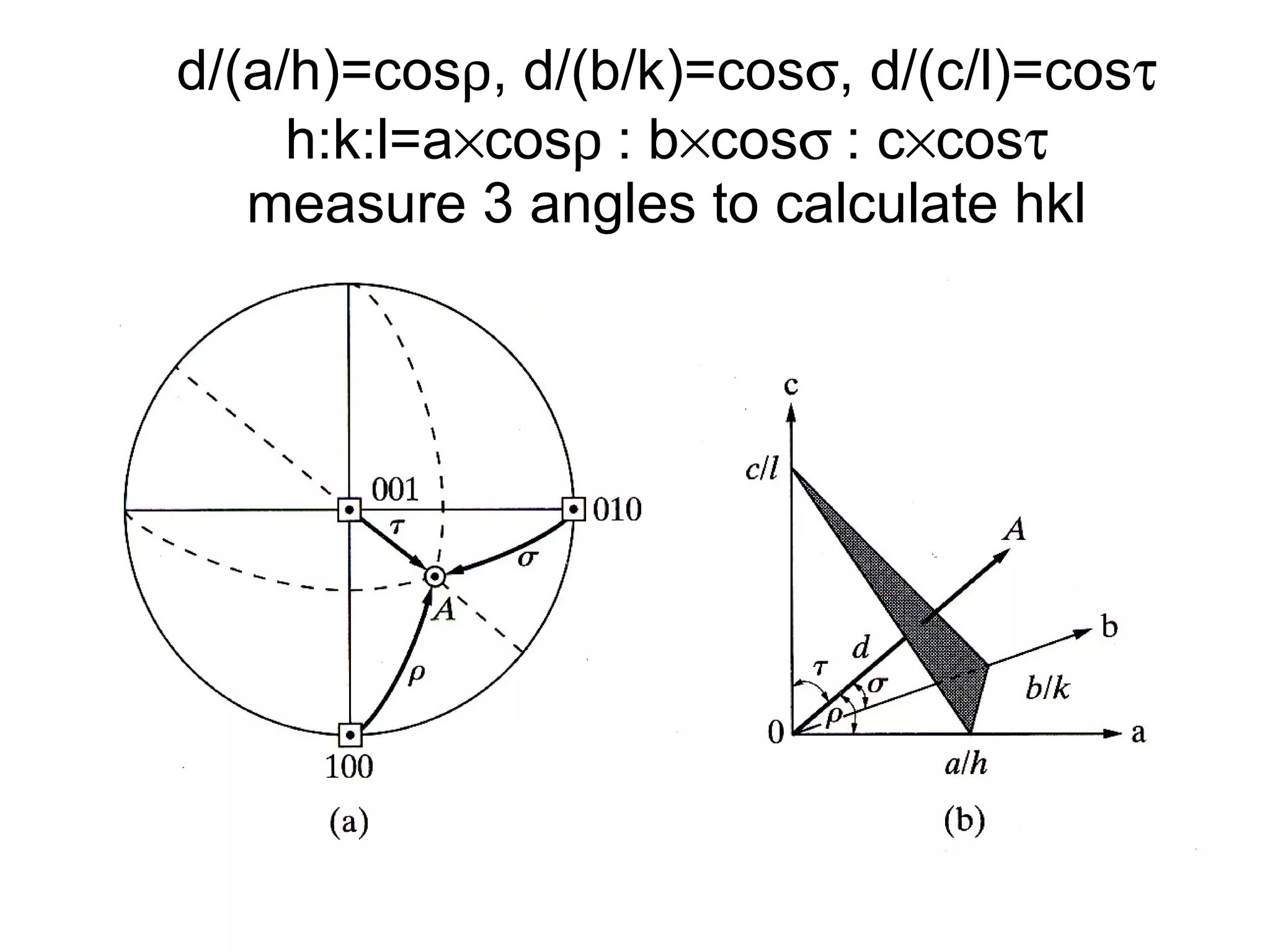
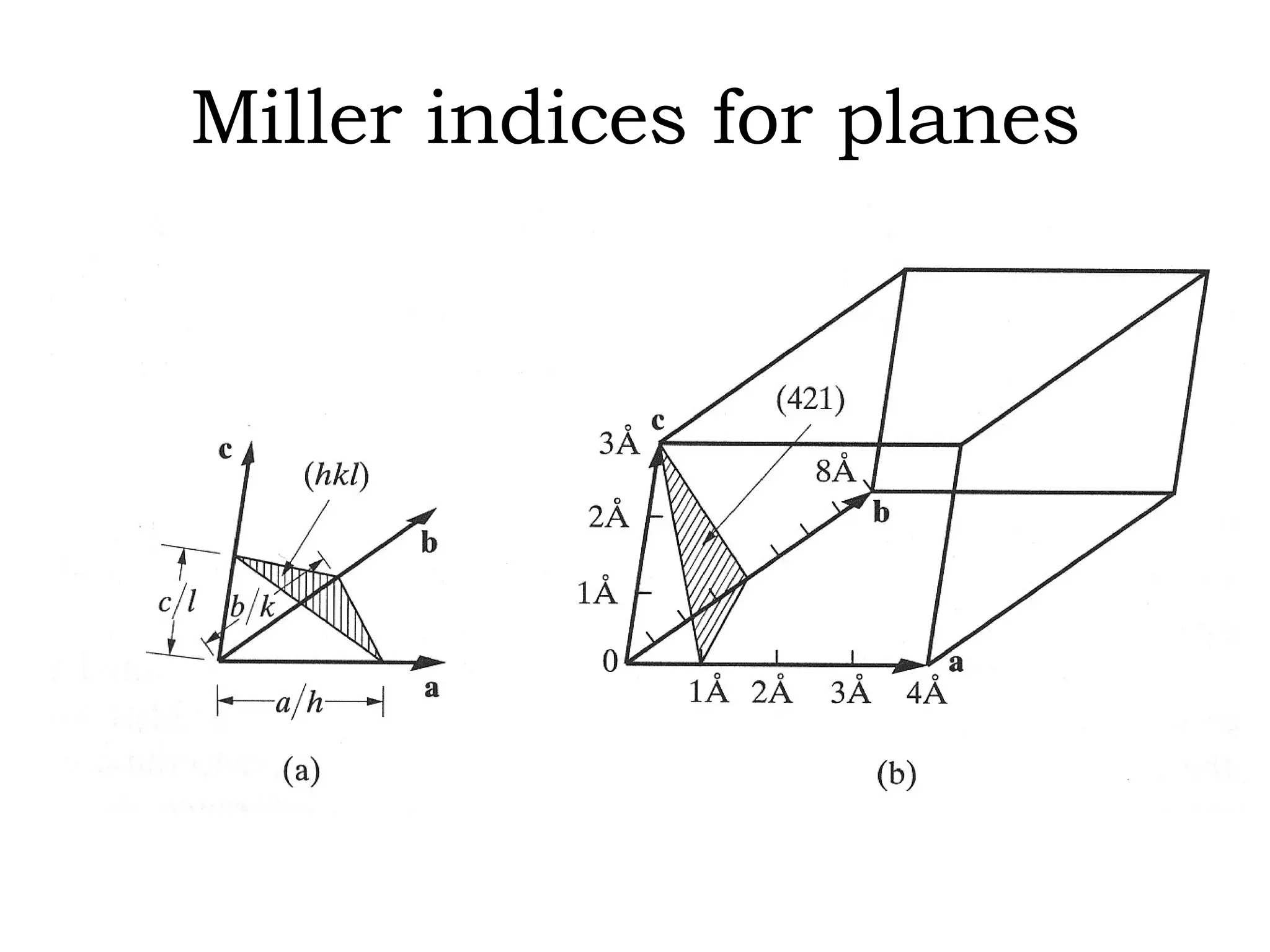
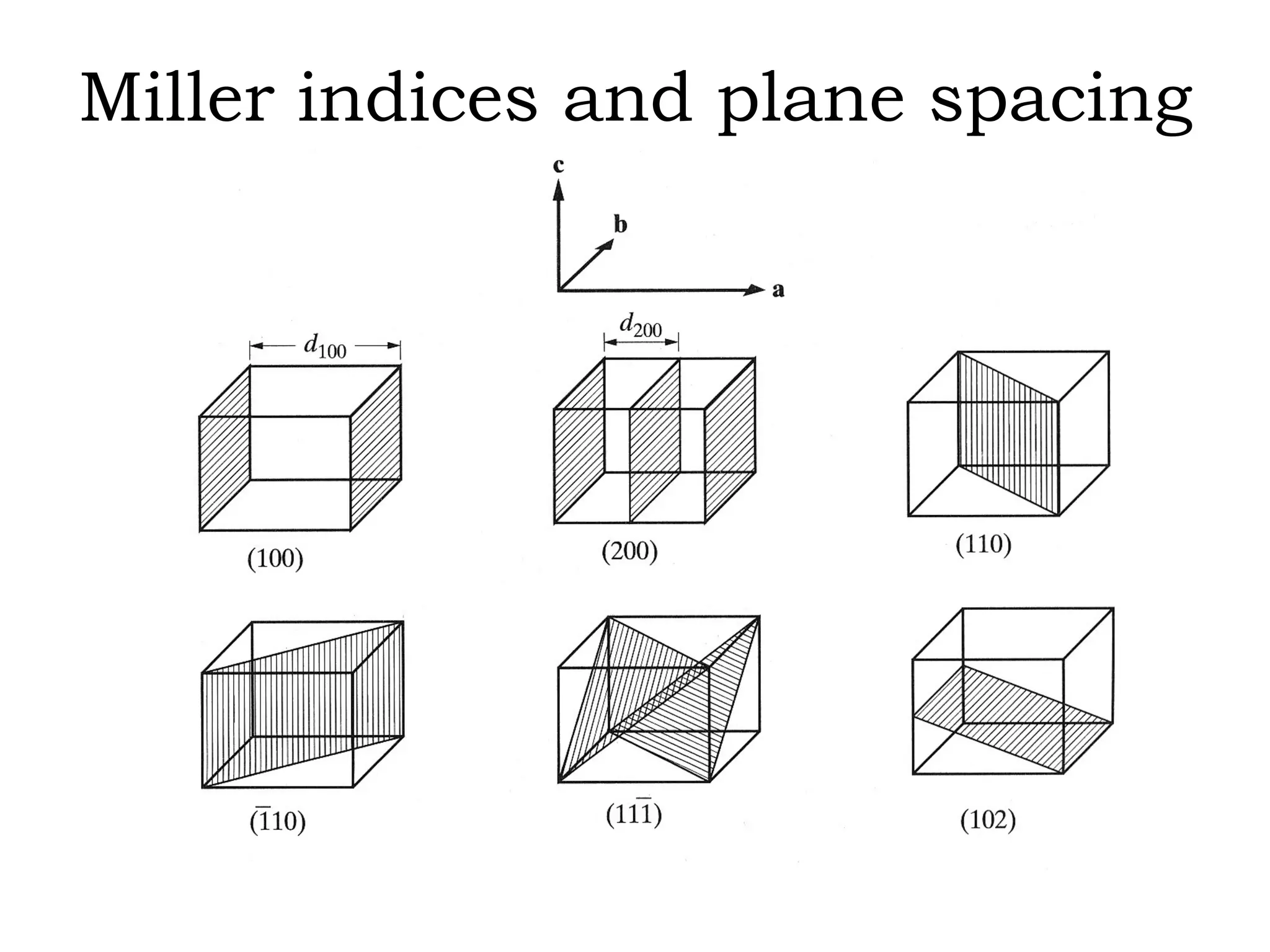
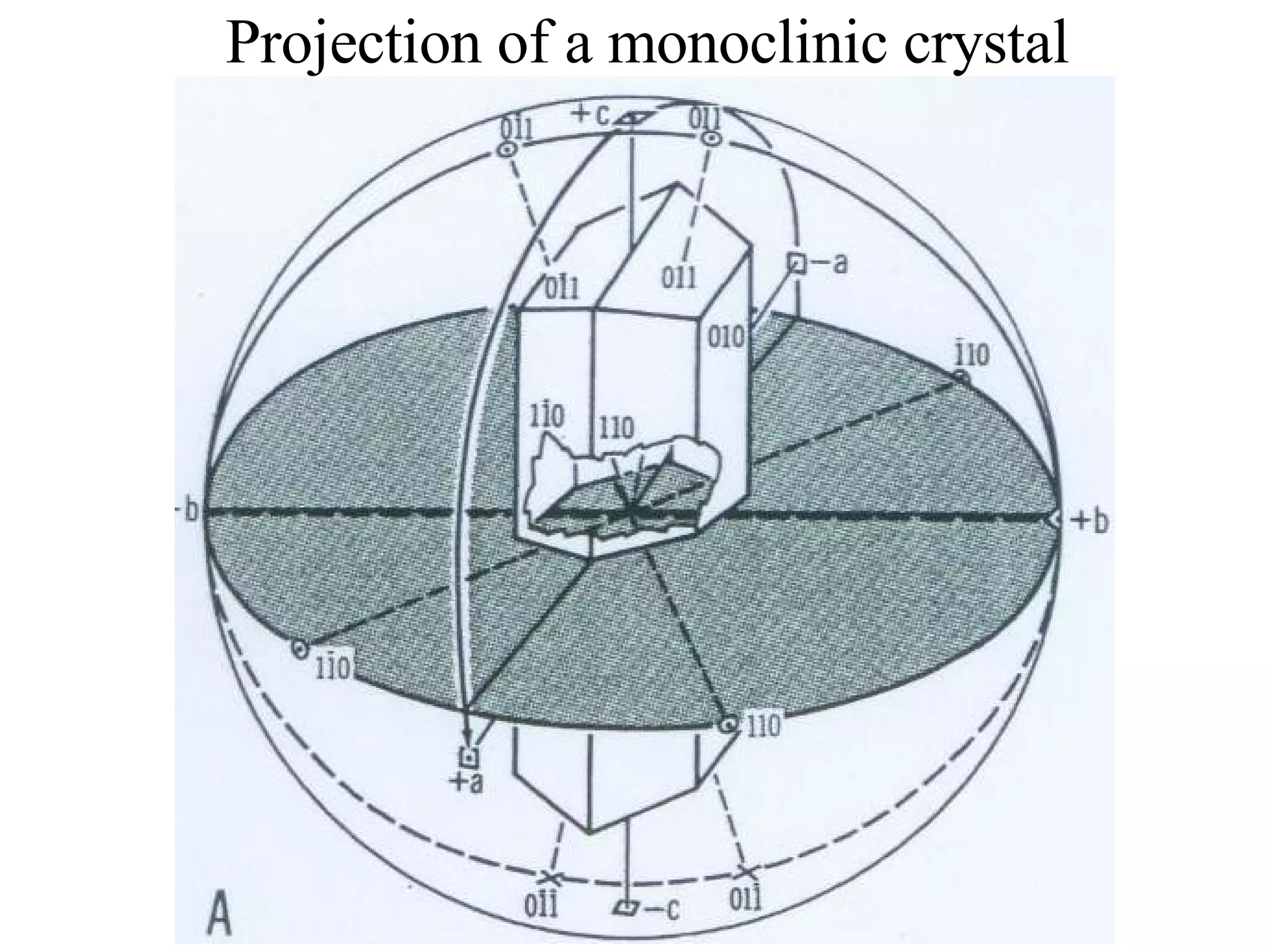
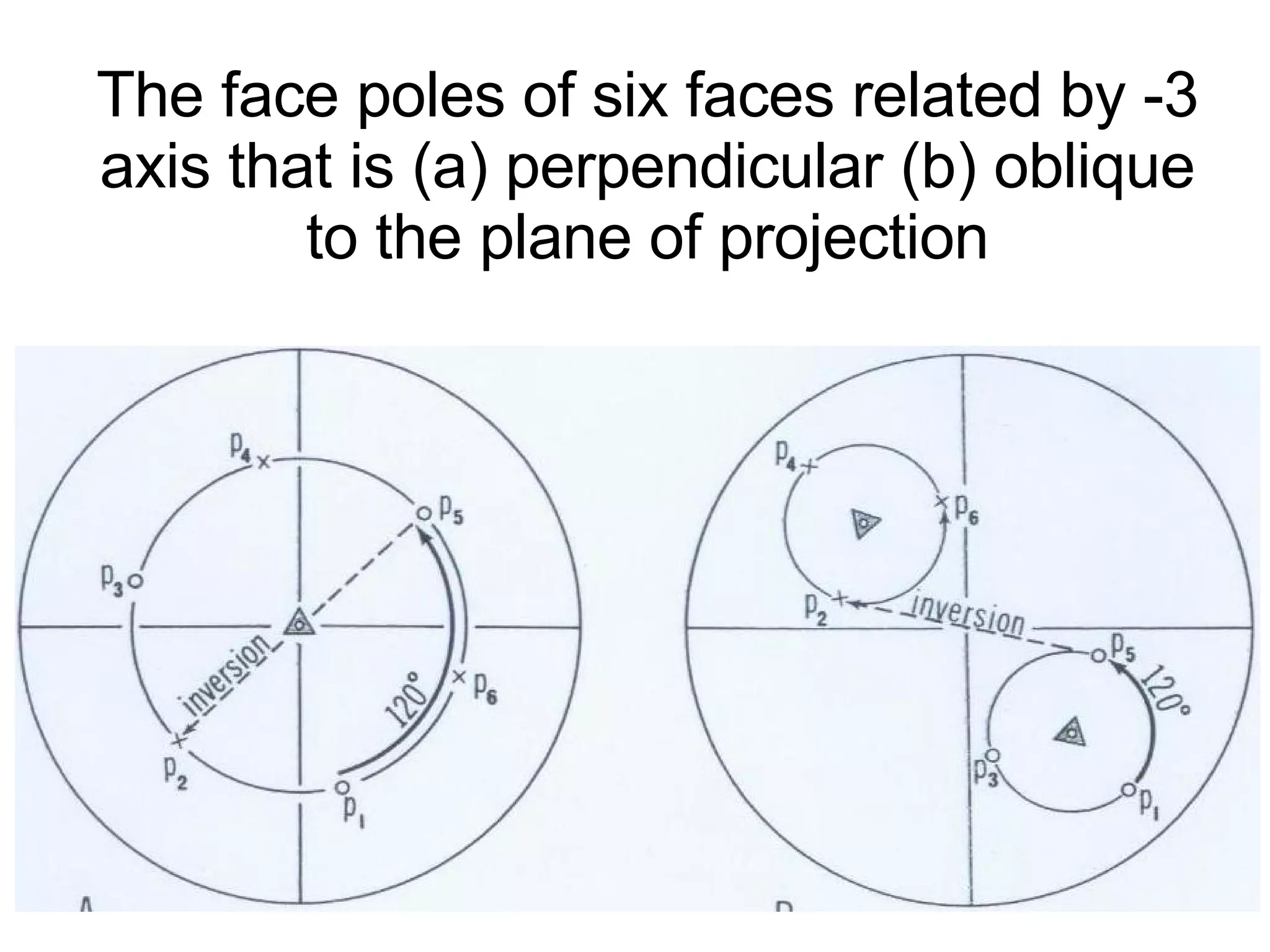
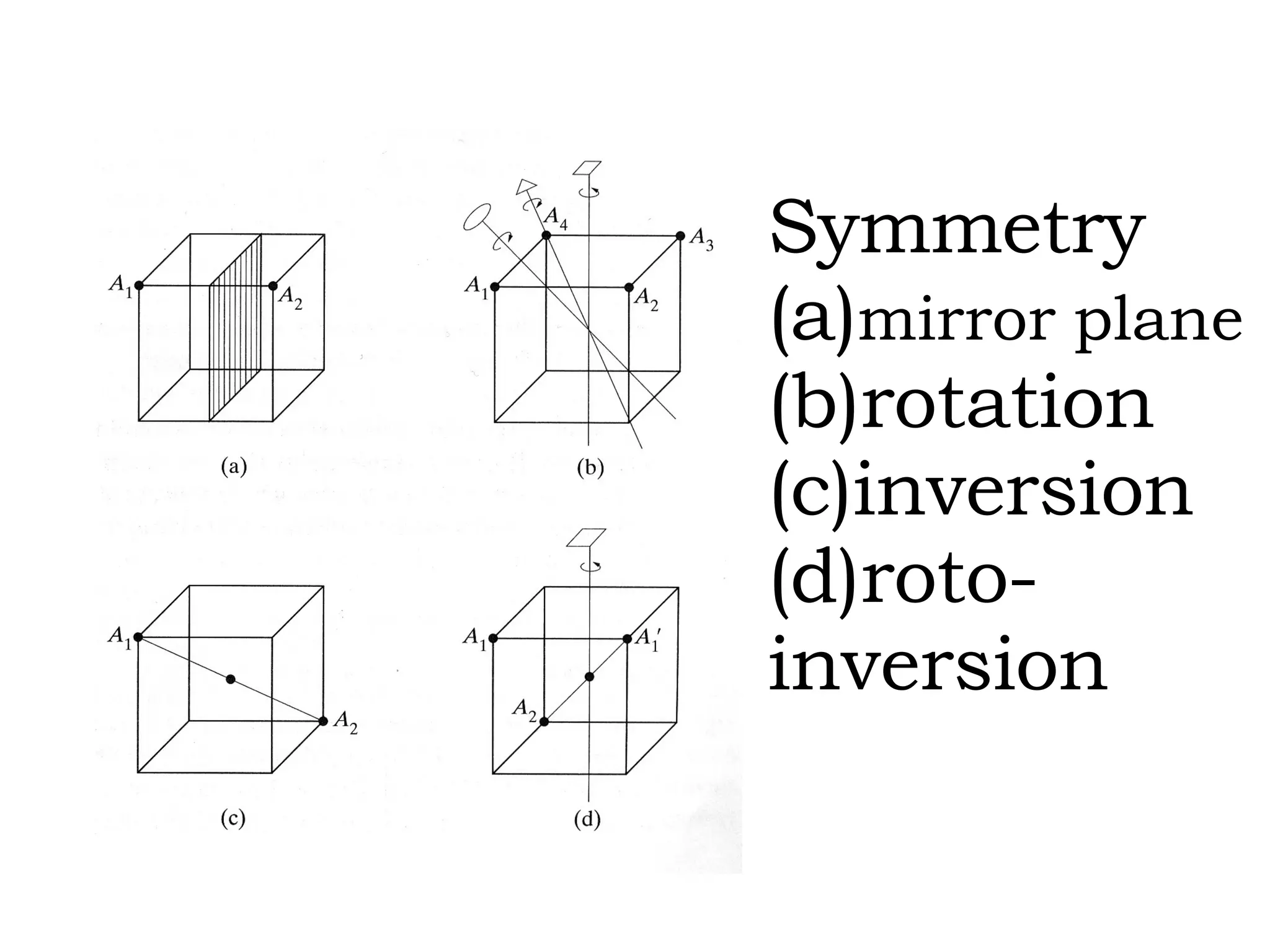
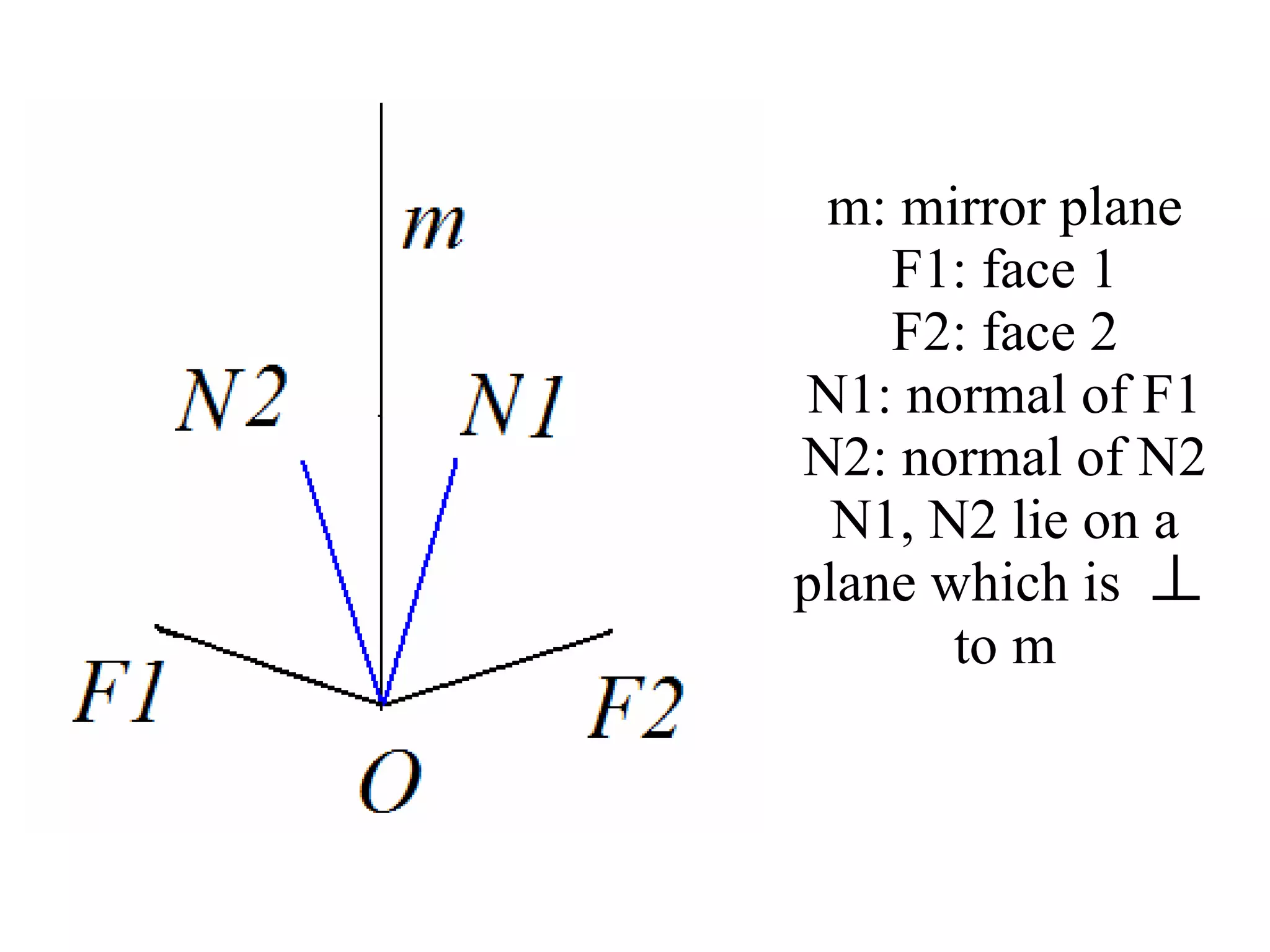
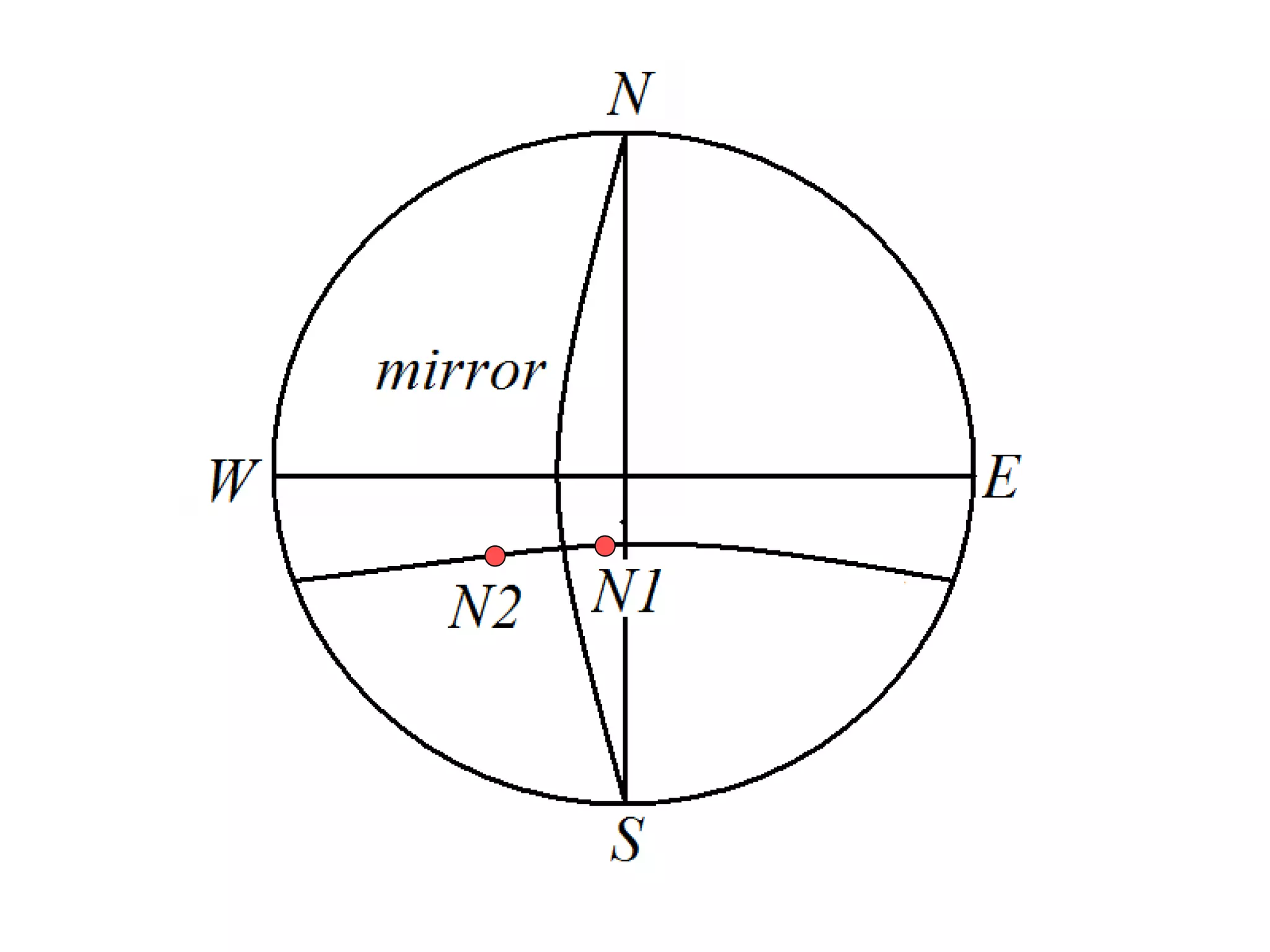
The document discusses crystal lattices and crystallography concepts including: - The 14 Bravais lattices that describe the geometric arrangements of points or atoms in crystal structures. - Miller indices for describing planes in crystal structures. - Reciprocal lattices and how they relate to direct crystal lattices. - Symmetry operations and elements that are present in different crystal systems. 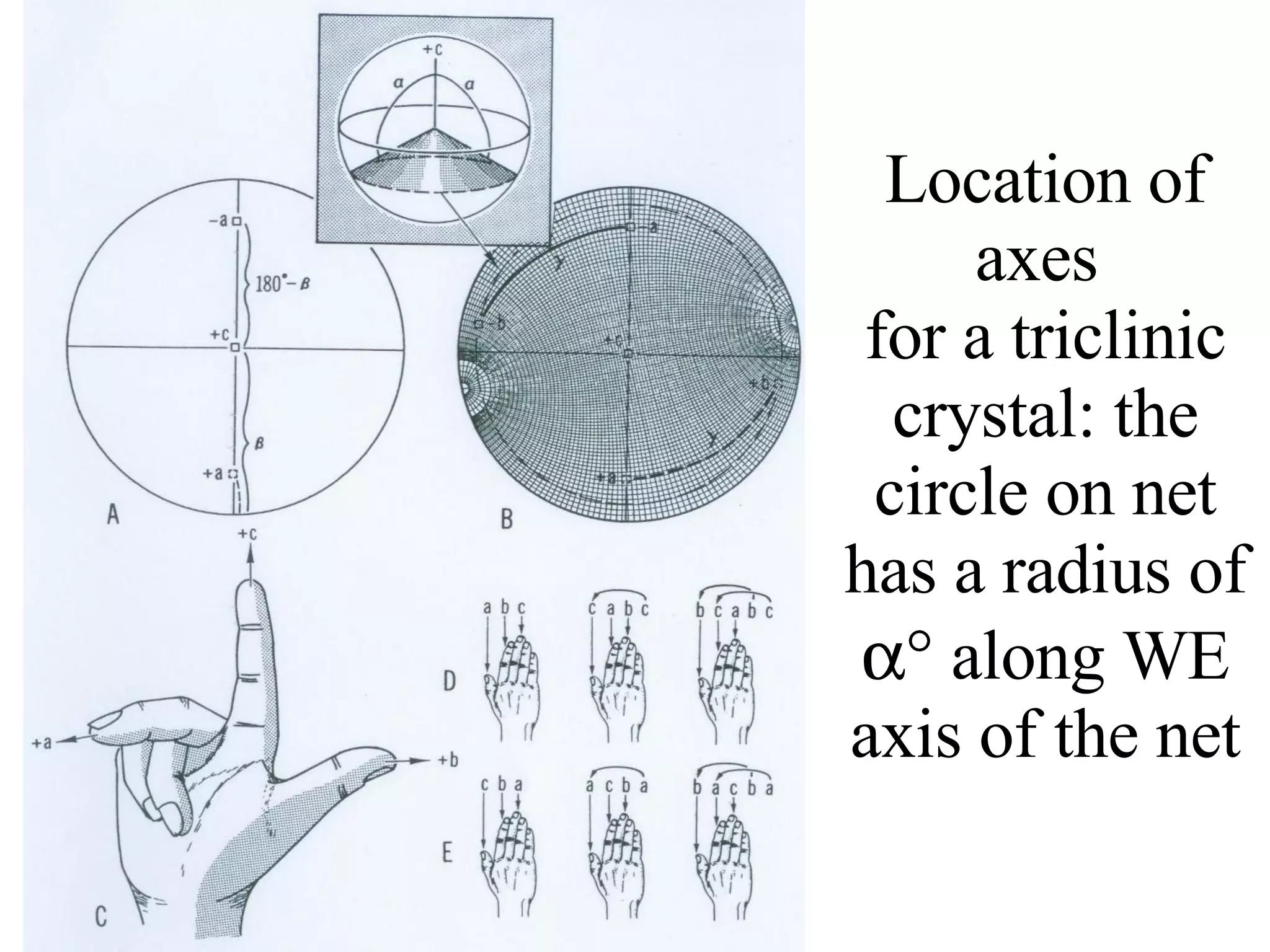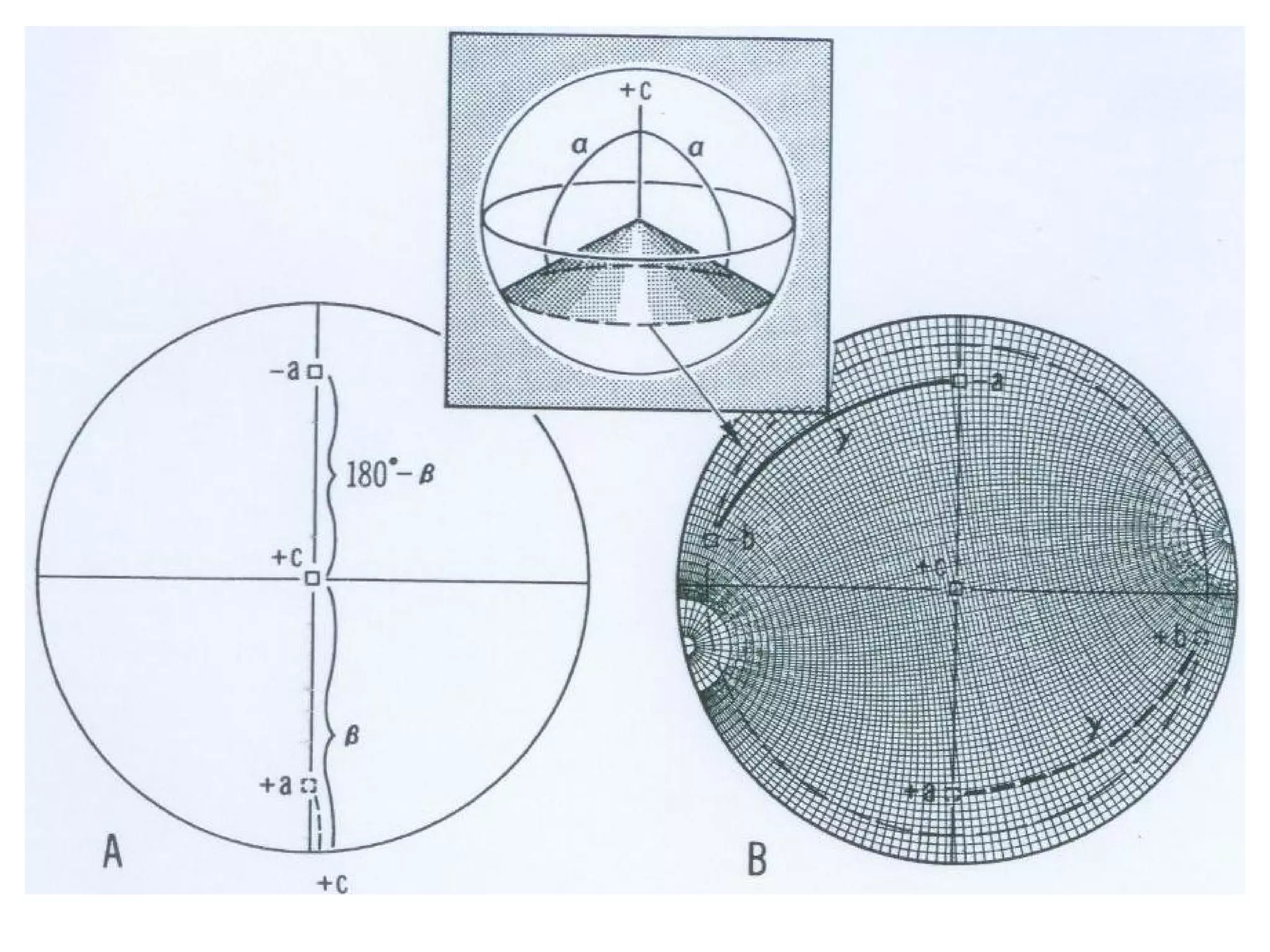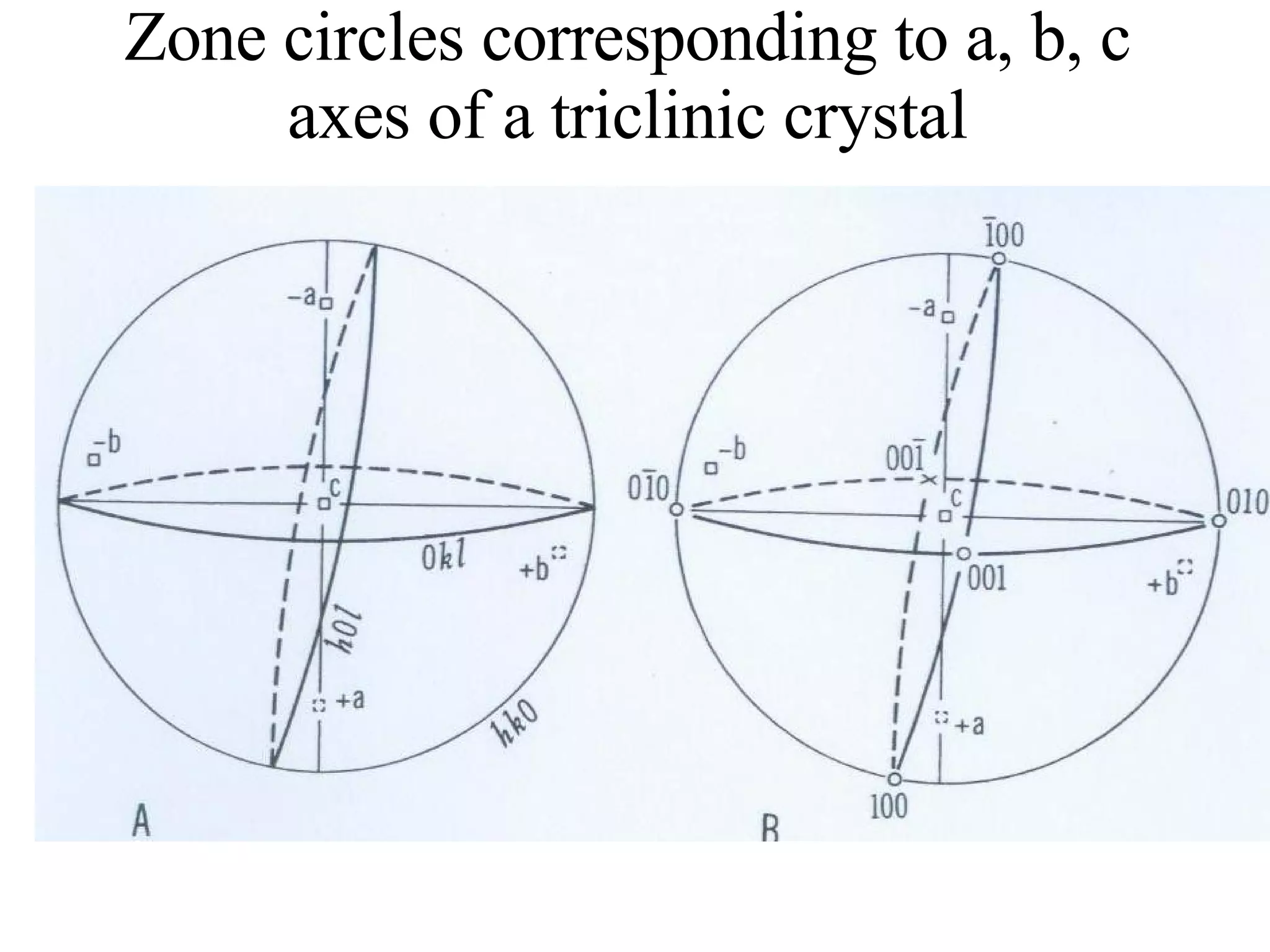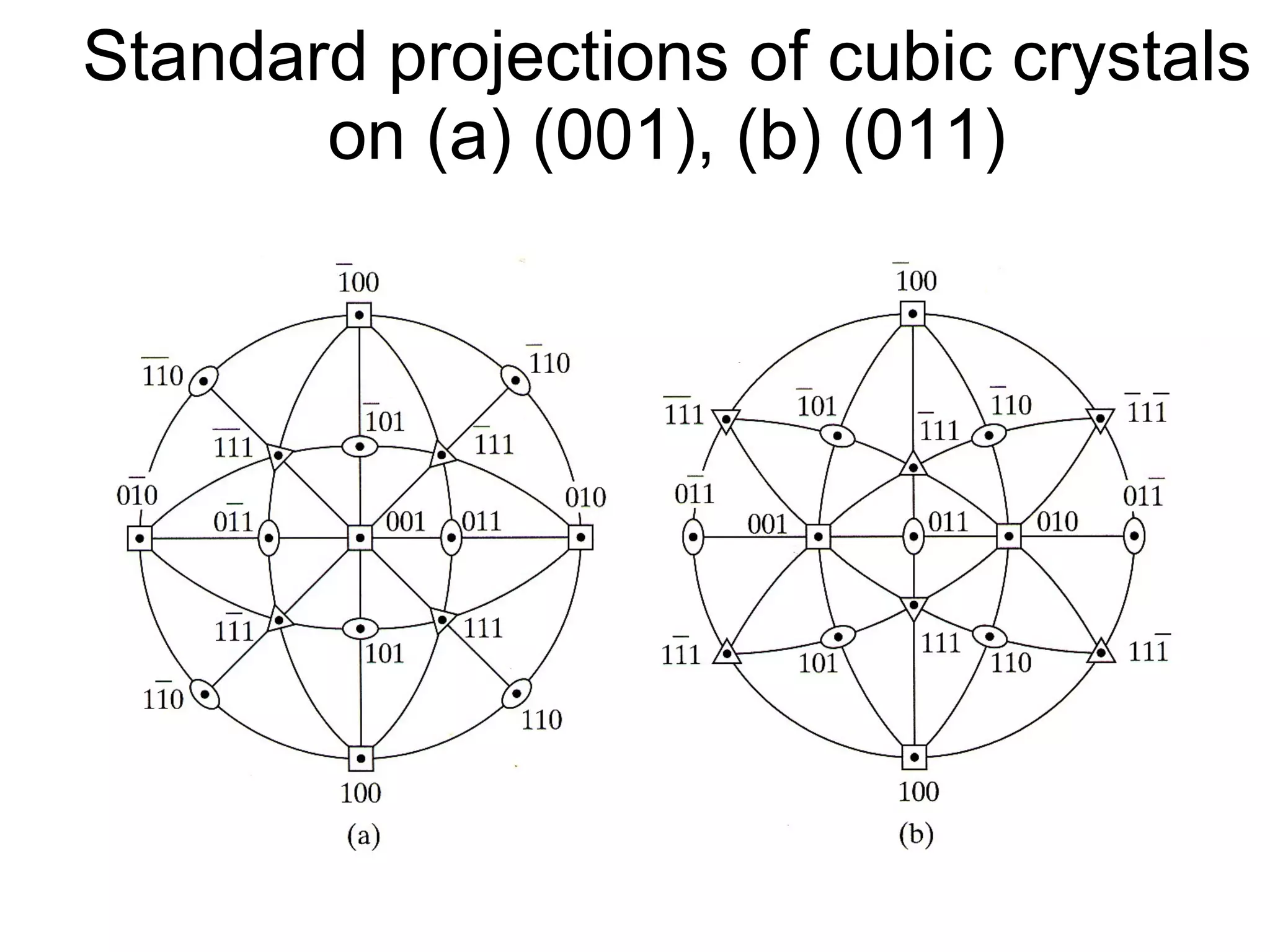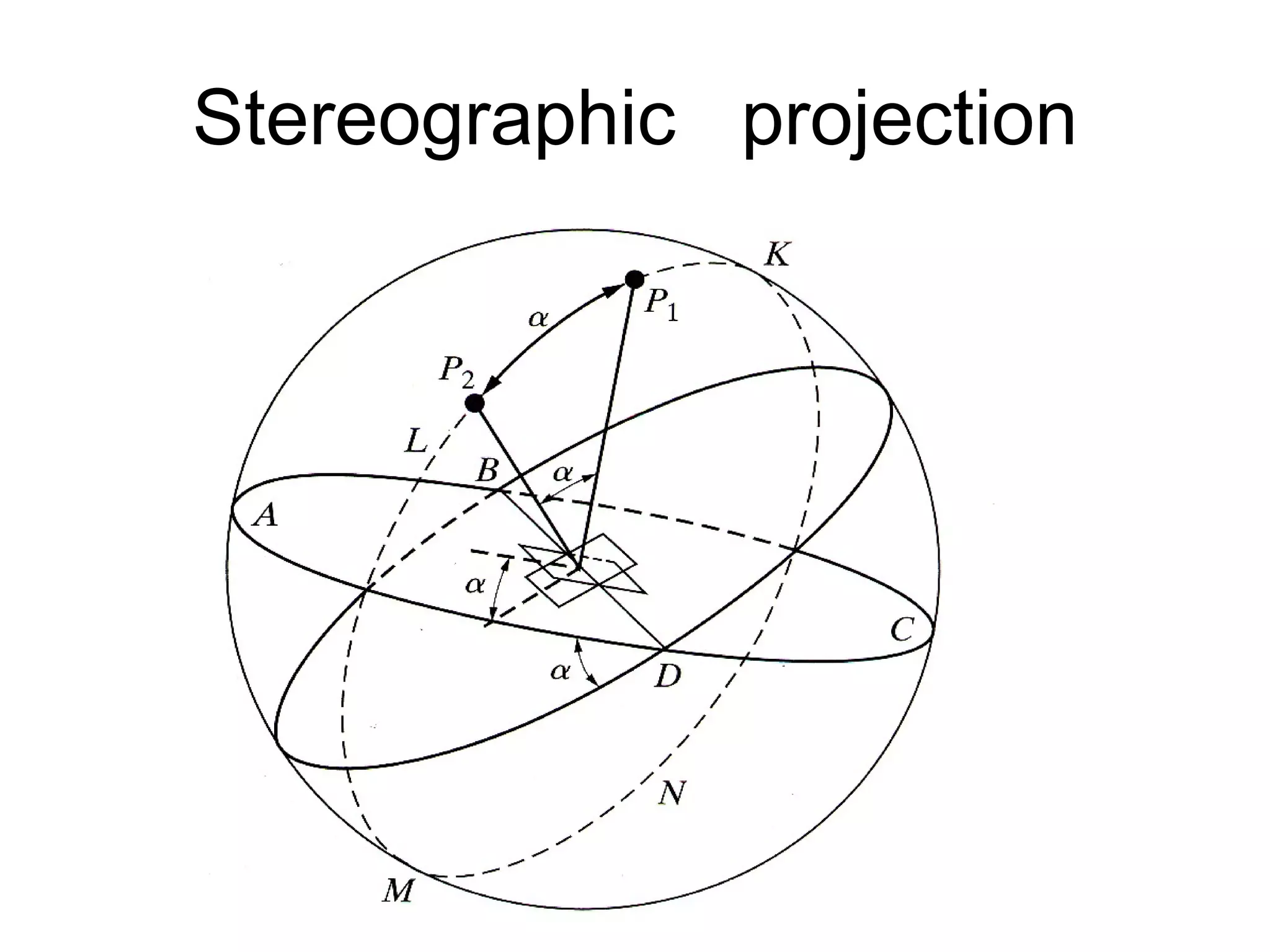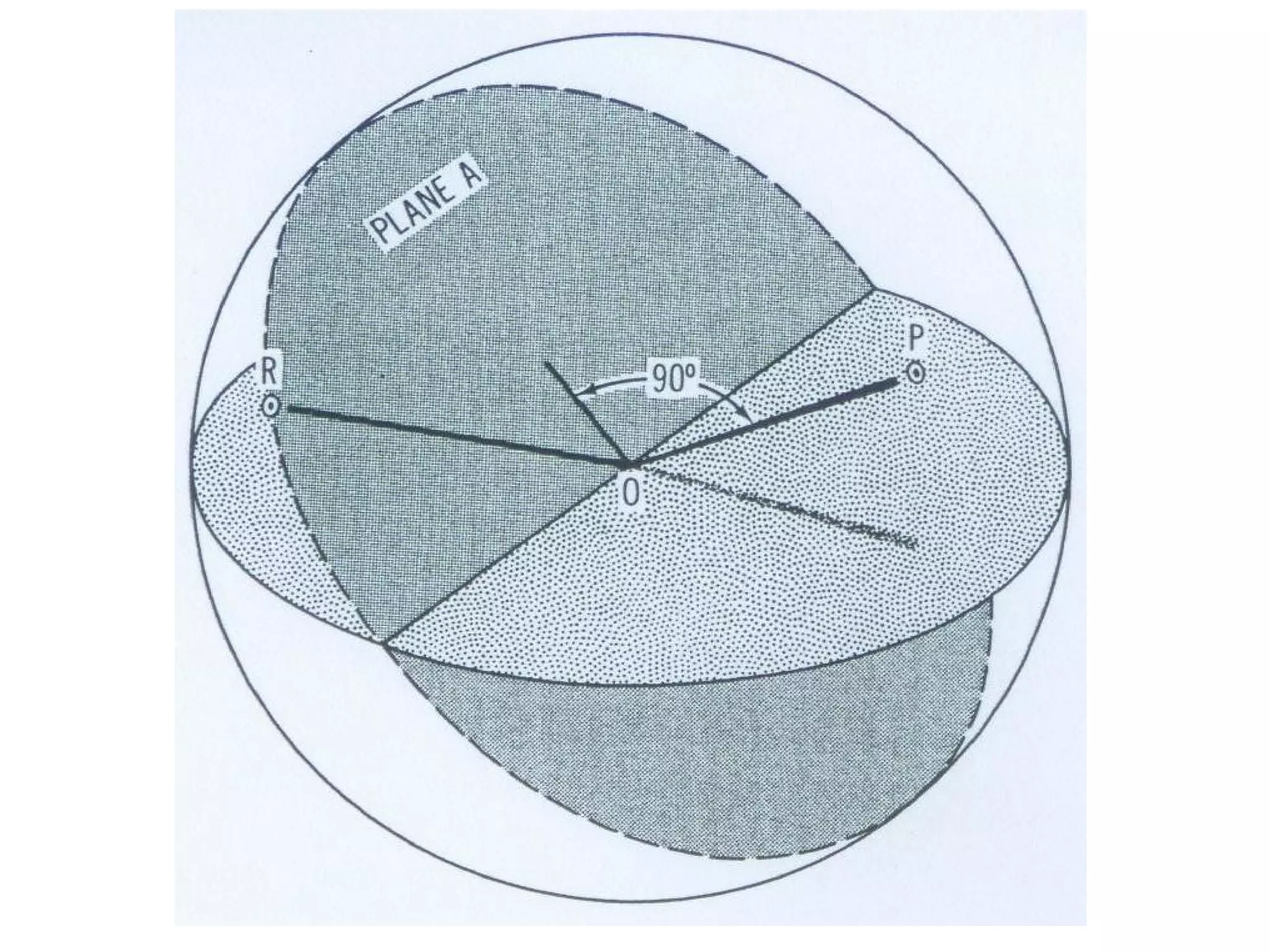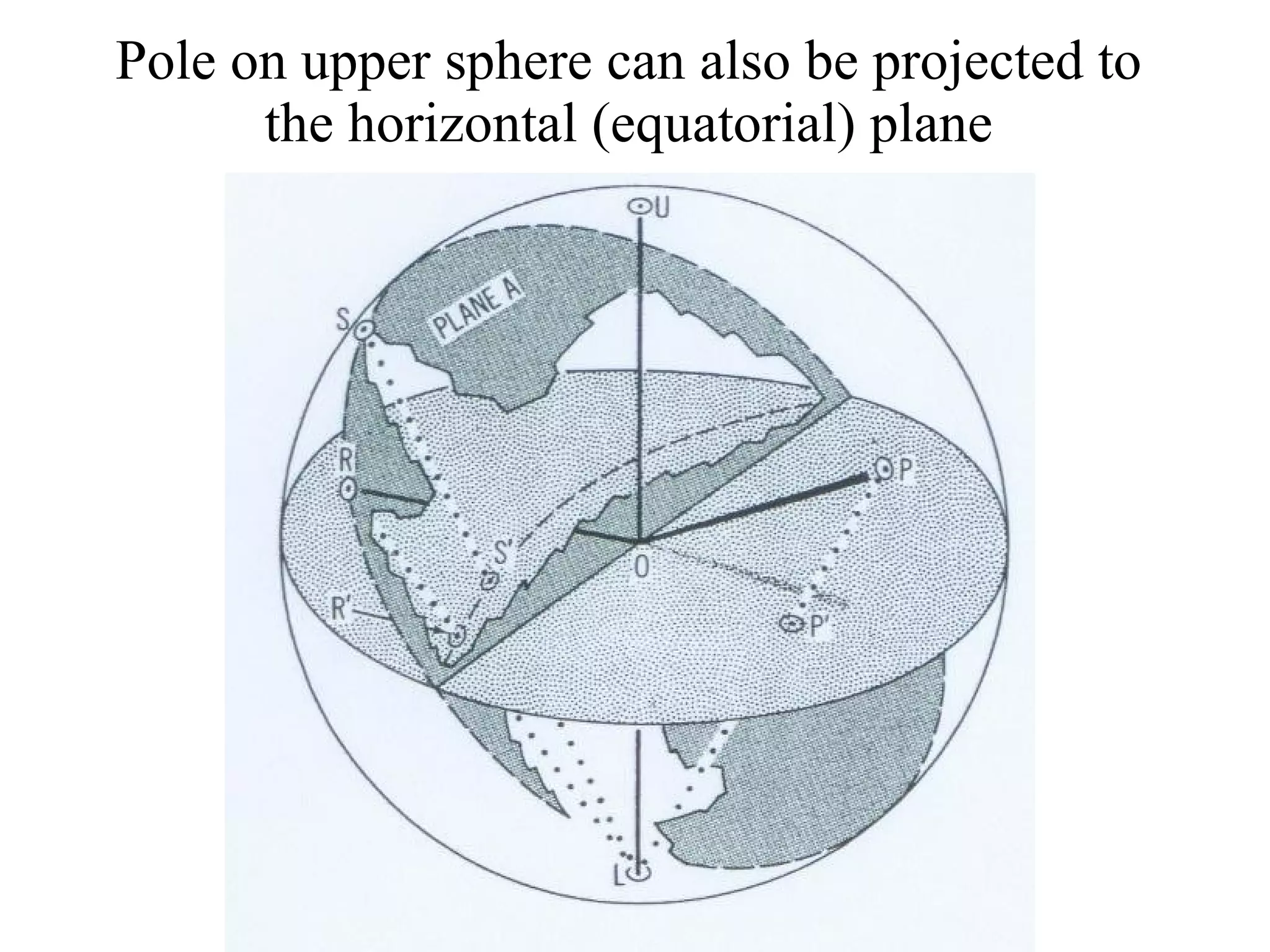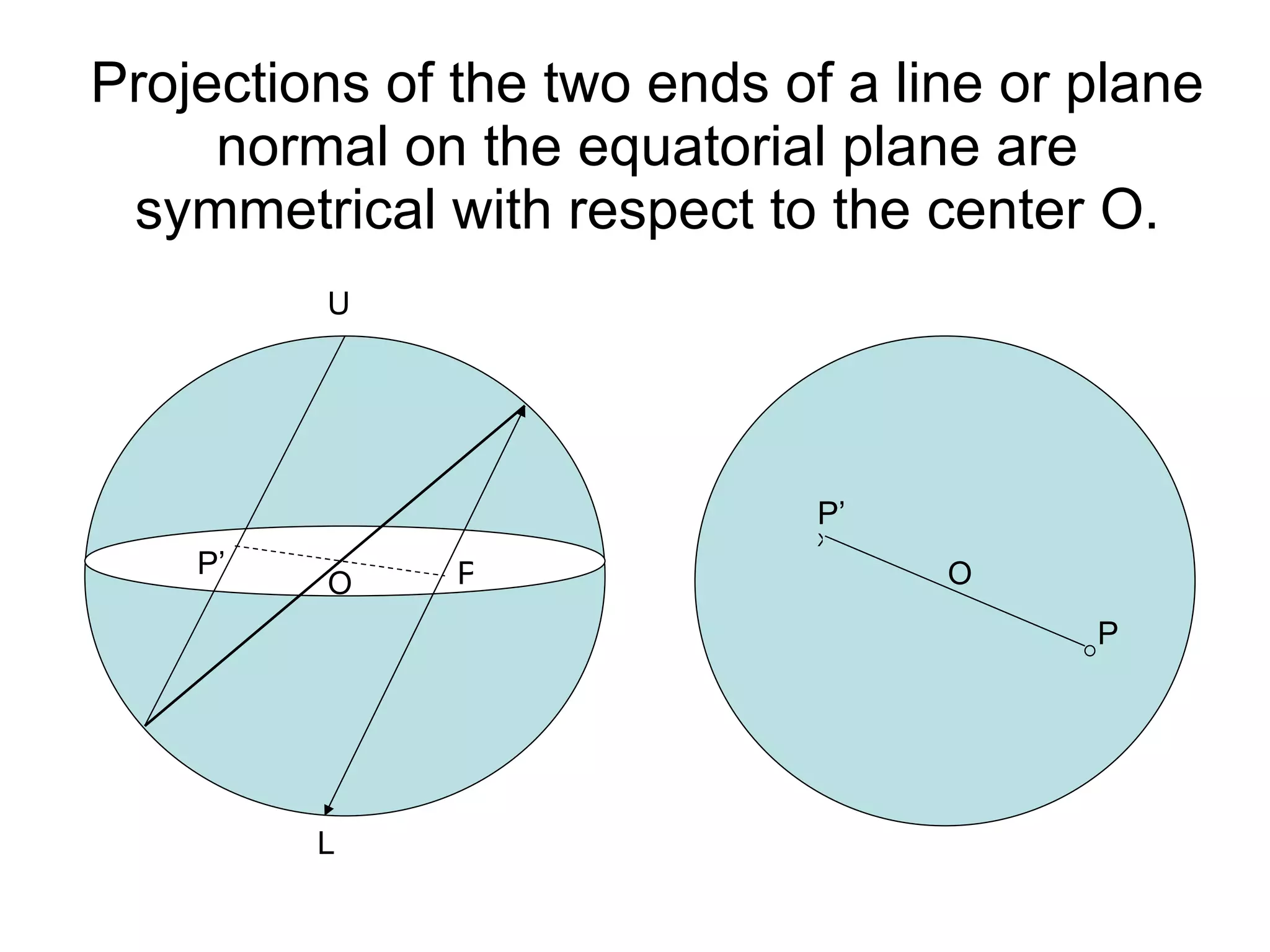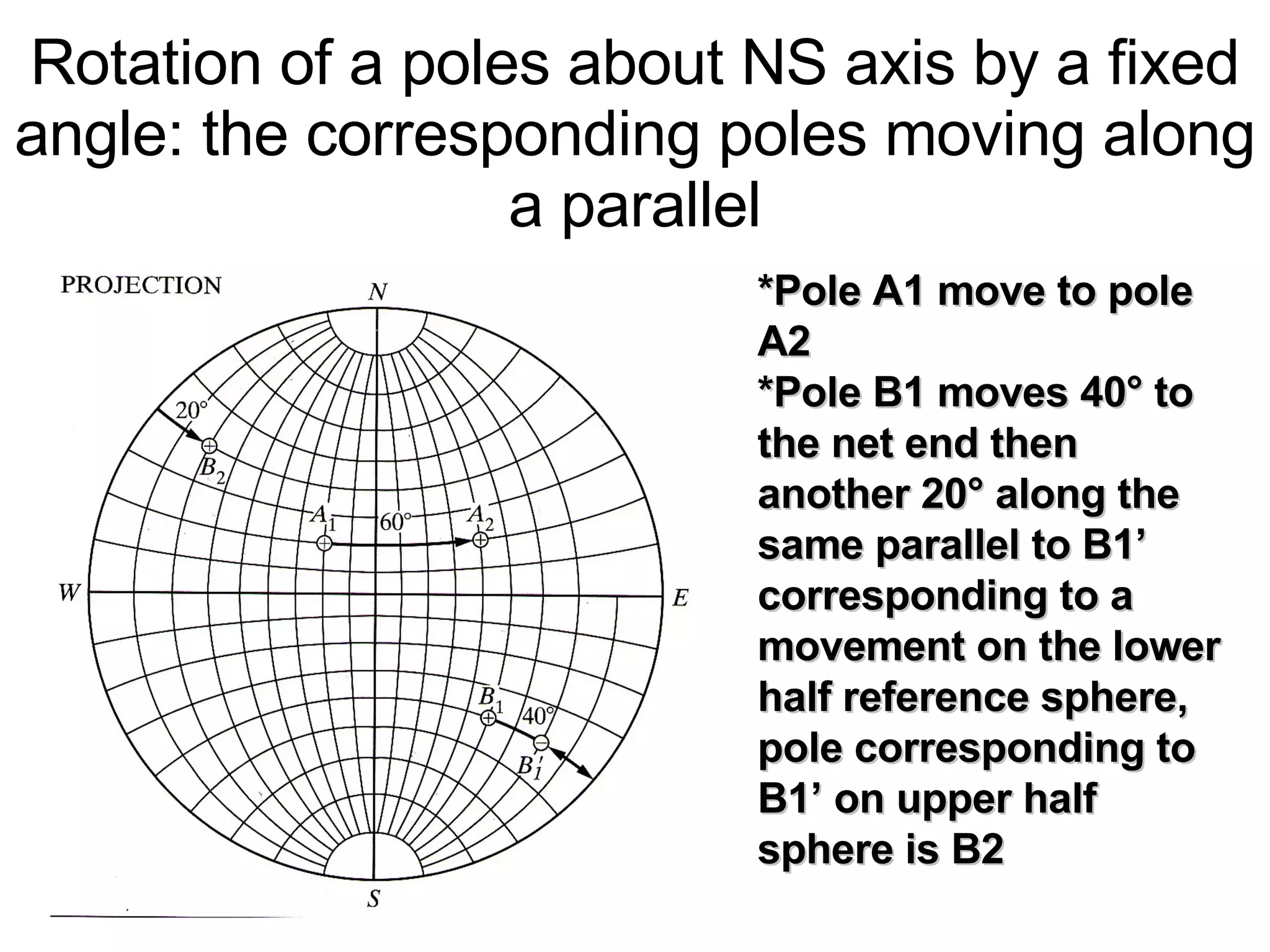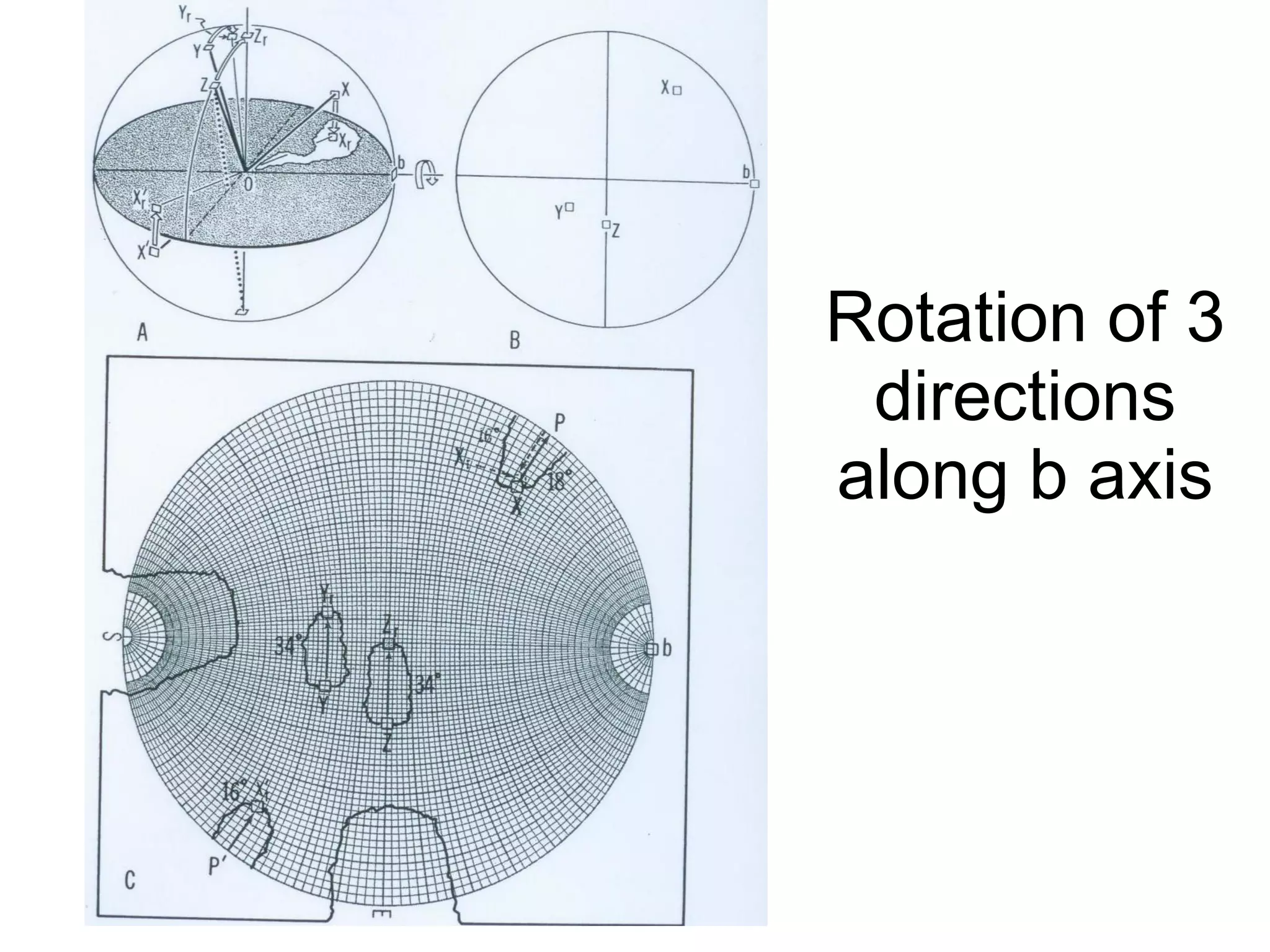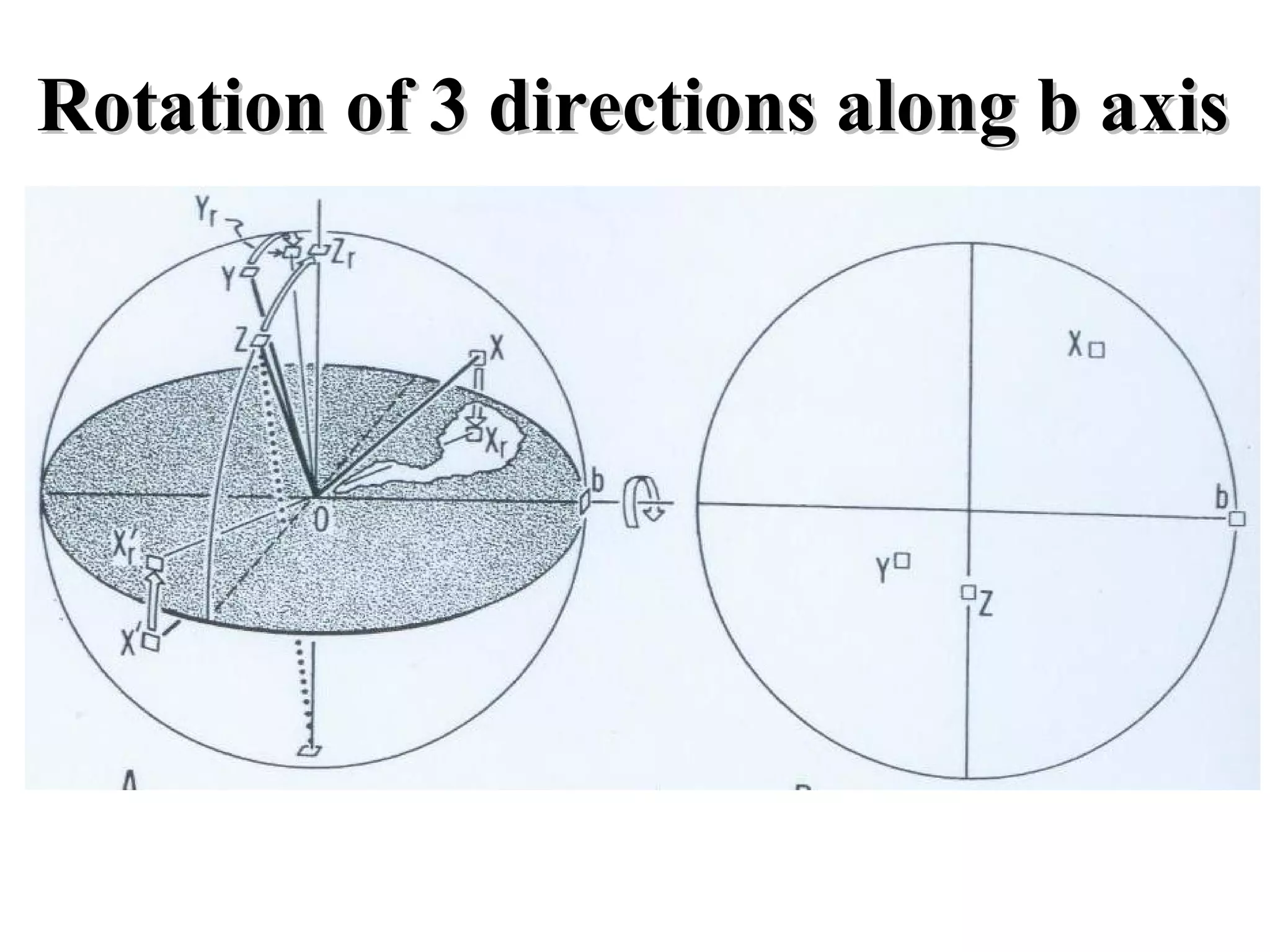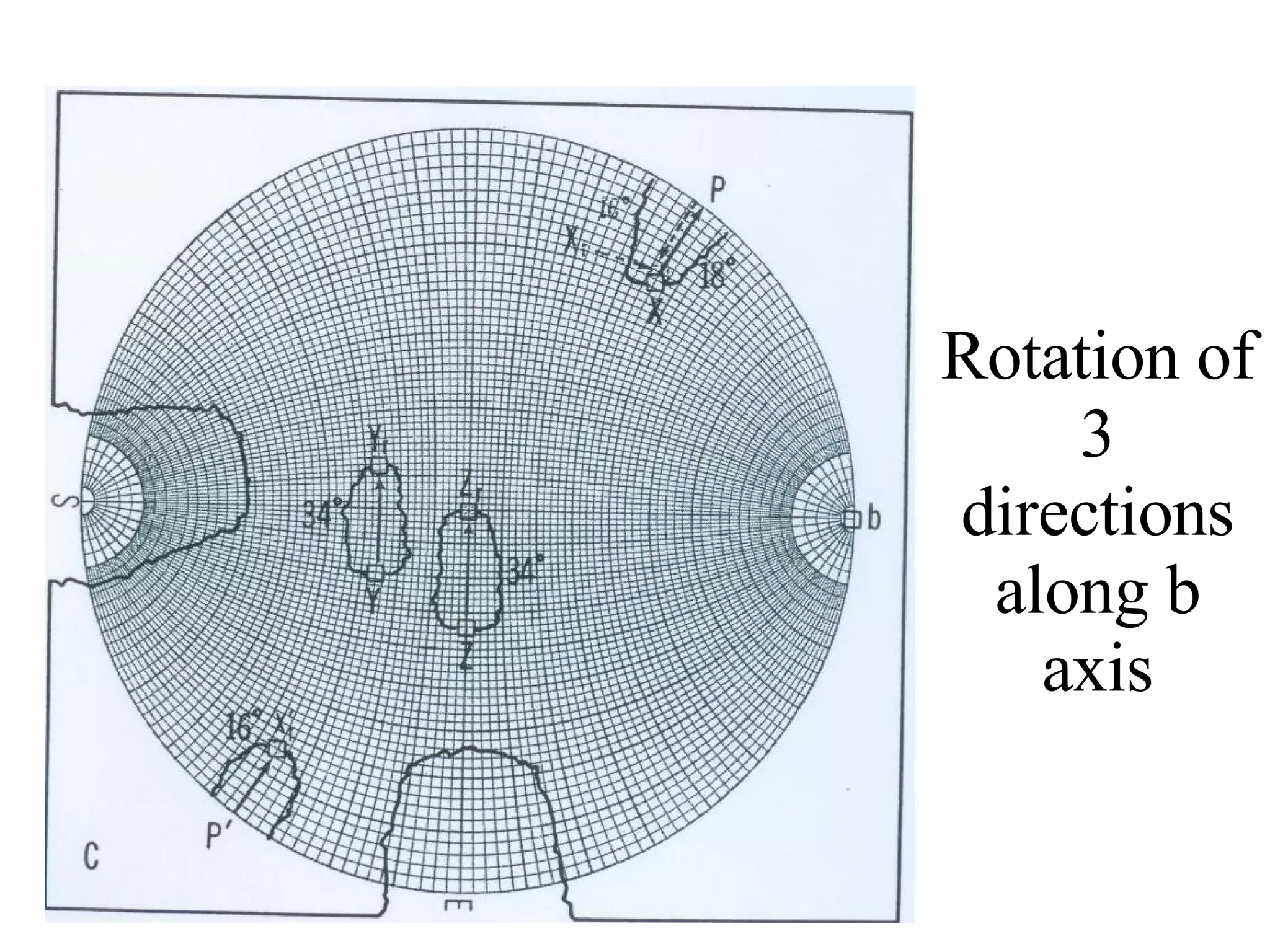- Stereographic projections for representing crystallographic planes and directions.

1. Space Lattice are non-coplanar vectors in space forming a basis { }

2. One dimensional lattice Two dimensional lattice

3. Three dimensional lattice

4. Lattice vectors and parameters

5. Indices of directions

6. Miller indices for planes

7. Miller indices and plane spacing

8. Two-dimensional lattice showing that lines of lowest indices have the greatest spacing and greatest density of lattice points

9. Reciprocal lattice

10. Illustration of crystal lattices and corresponding reciprocal lattices for a cubic system

11. Illustration of crystal lattices and corresponding reciprocal lattices for a a hexagonal system

12. If then and perpendicular to (hkl) plane

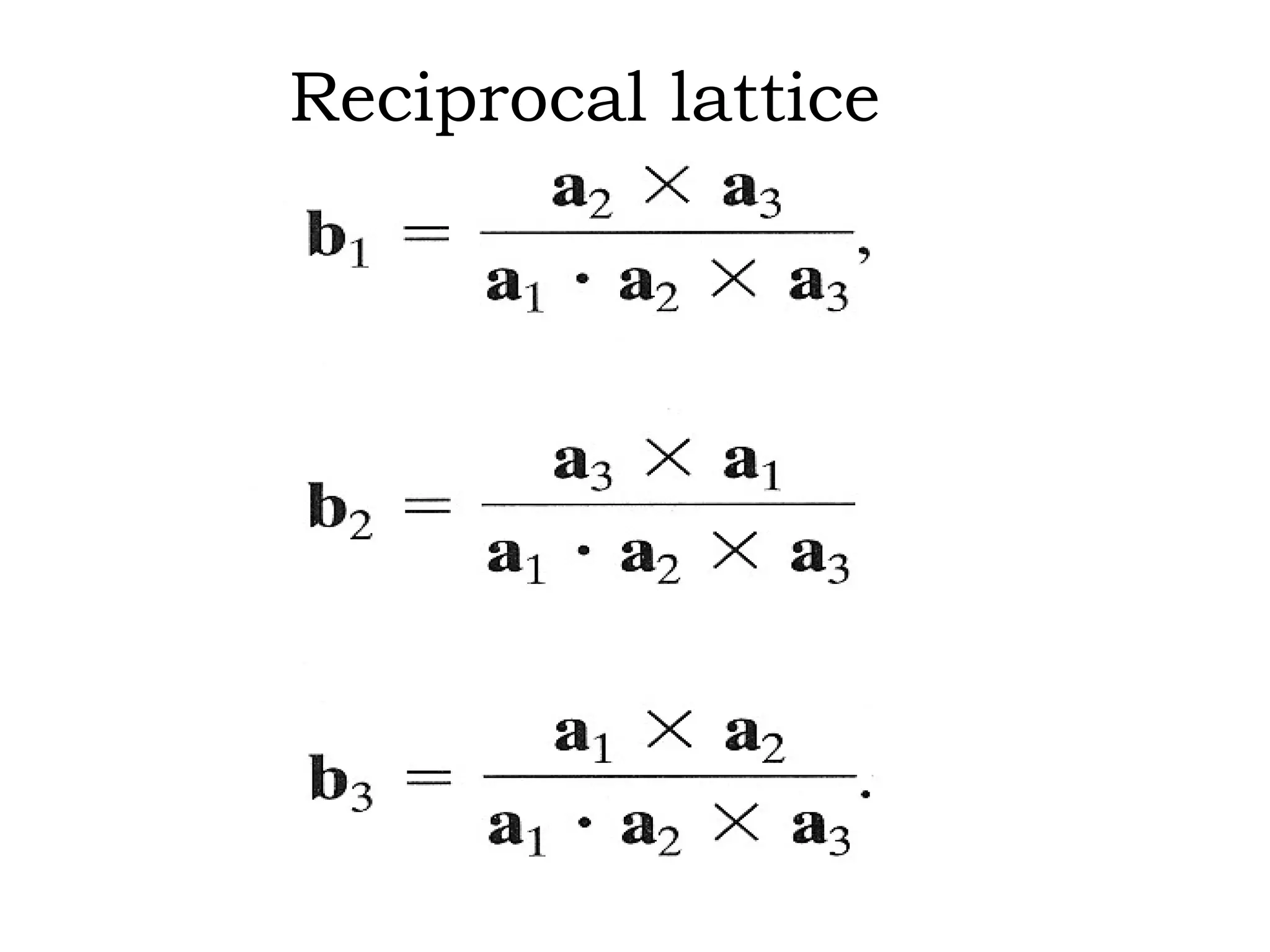
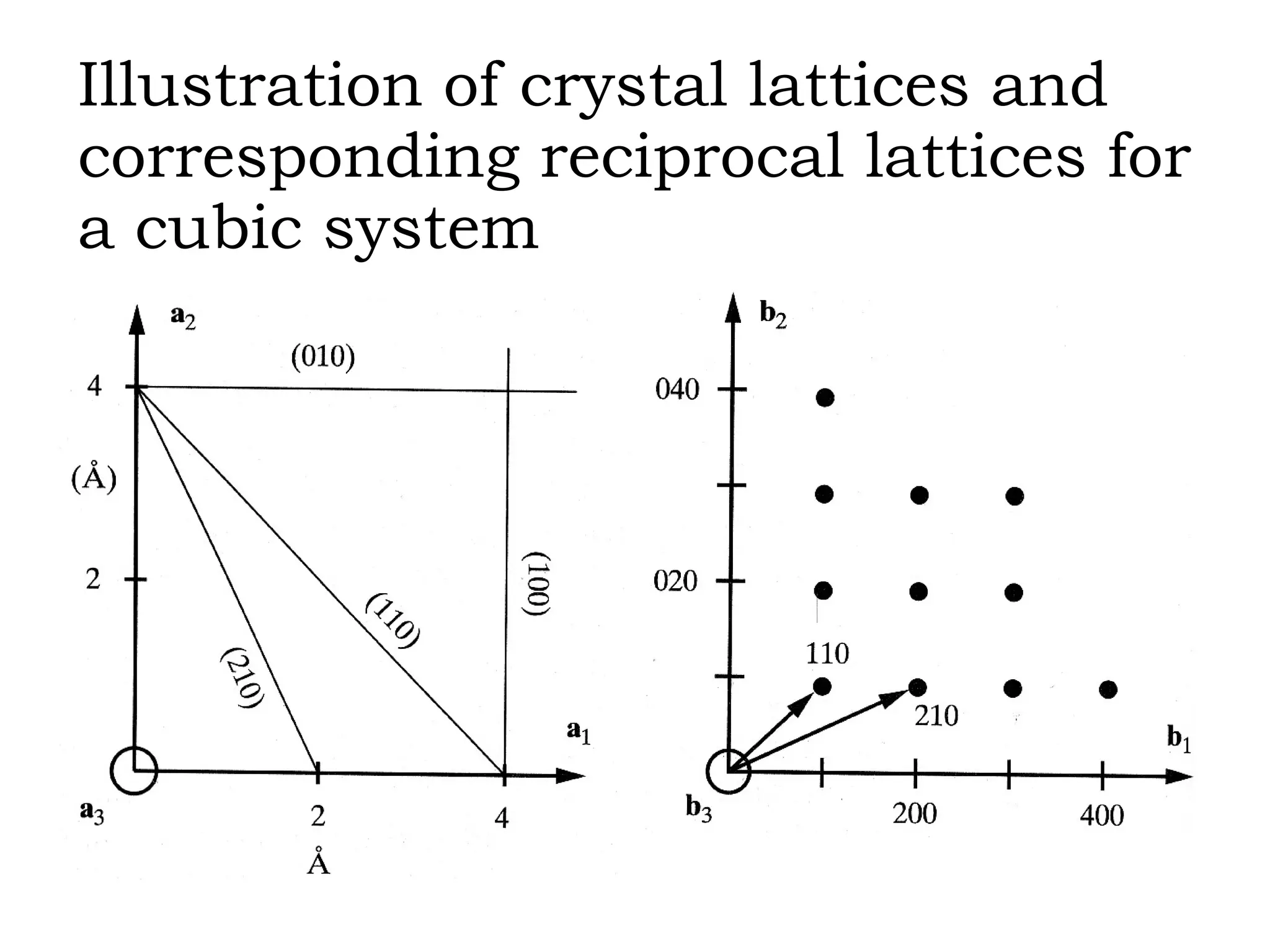
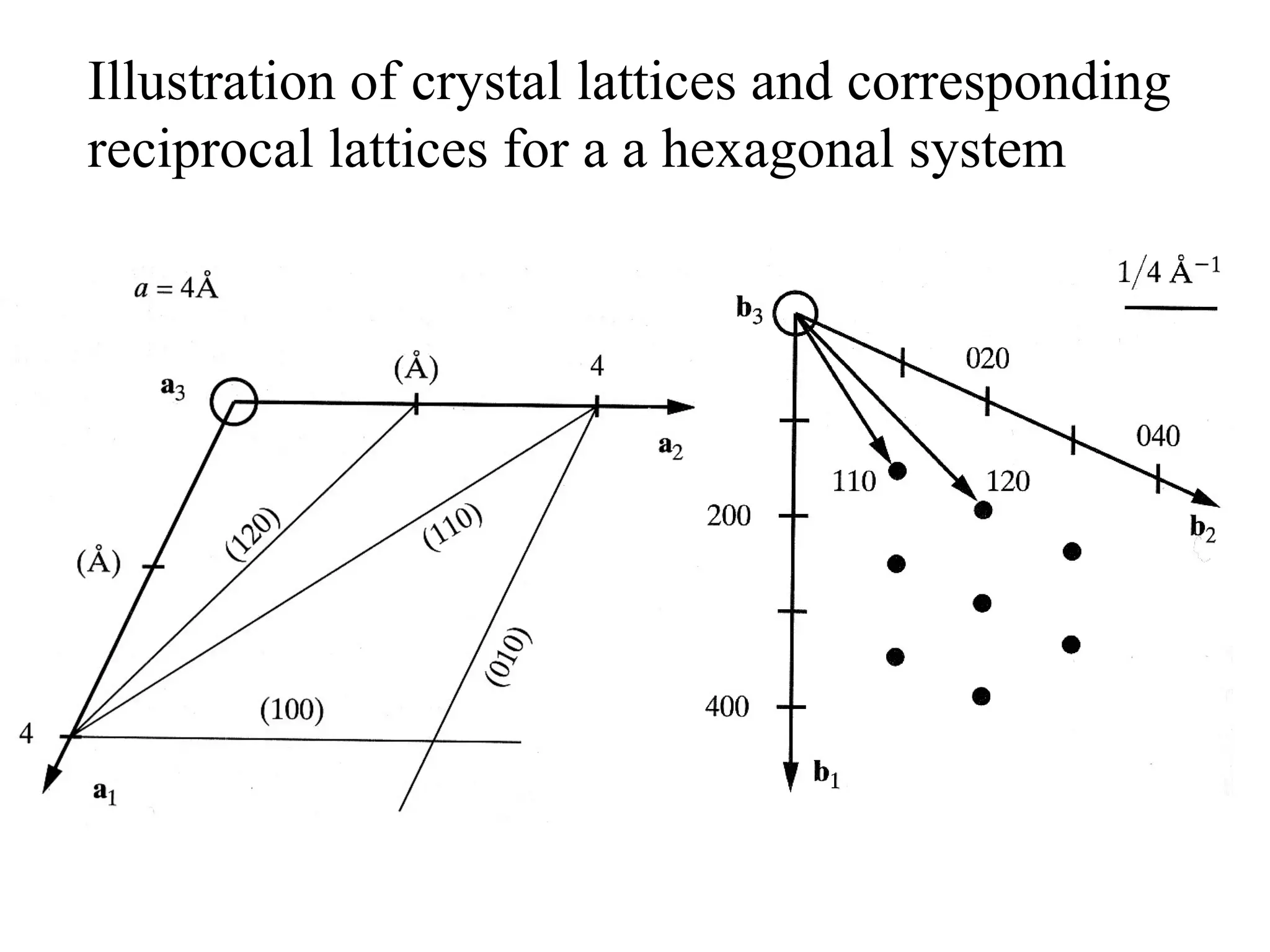
13. If then and perpendicular to (hkl) plane Proof: H • ( a 1 /h- a 2 /k) = H • ( a 1 /h- a 3 /l)=0 a 1 /h• H /| H |=[1/h 0 0] • [hkl]*/| H |=1/| H |=d hkl H a 1 a 2 a 3

14. Symmetry (a) mirror plane (b)rotation (c)inversion (d)roto- inversion

15. Symmetry operation

16. Crystal system

17. The 14 Bravais lattices

18. The fourteen Bravais lattices Simple cubic lattices nitrogen - simple cubic copper - face centered cubic body centered cubic Cubic lattices a 1 = a 2 = a 3 α = β = γ = 90 o

19. Tetragonal lattices a1 = a2 ≠ a3 α = β = γ = 90  simple tetragonal Body centered Tetragonal

20. Orthorhombic lattices a1 ≠ a2 ≠ a3 α = β = γ = 90  simple orthorhombic Base centered orthorhombic Body centered orthorhombic Face centered orthorhombic

21. Monoclinic lattices a1 ≠ a2 ≠ a3 α = γ = 90  ≠ β (2nd setting) α = β = 90  ≠ γ (1st setting) Simple monoclinic Base centered monoclinic

22. Triclinic lattice a1 ≠ a2 ≠ a3 α ≠ β ≠ γ Simple triclinic

23. Hexagonal lattice a1 = a2 ≠ a3 α = β = 90  , γ = 120  lanthanum - hexagonal

24. Trigonal (Rhombohedral) lattice a1 = a2 = a3 α = β = γ ≠ 90  mercury - trigonal

25. Relation between rhombo-hedral and hexagonal lattices

26. Relation of tetragonal C lattice to tetragonal P lattice

27. Extension of lattice points through space by the unit cell vectors a, b, c

28. Symmetry elements

29. Primitive and non-primitive cells Face-centerd cubic point lattice referred to cubic and rhombo-hedral cells

30. All shaded planes in the cubic lattice shown are planes of the zone{001}

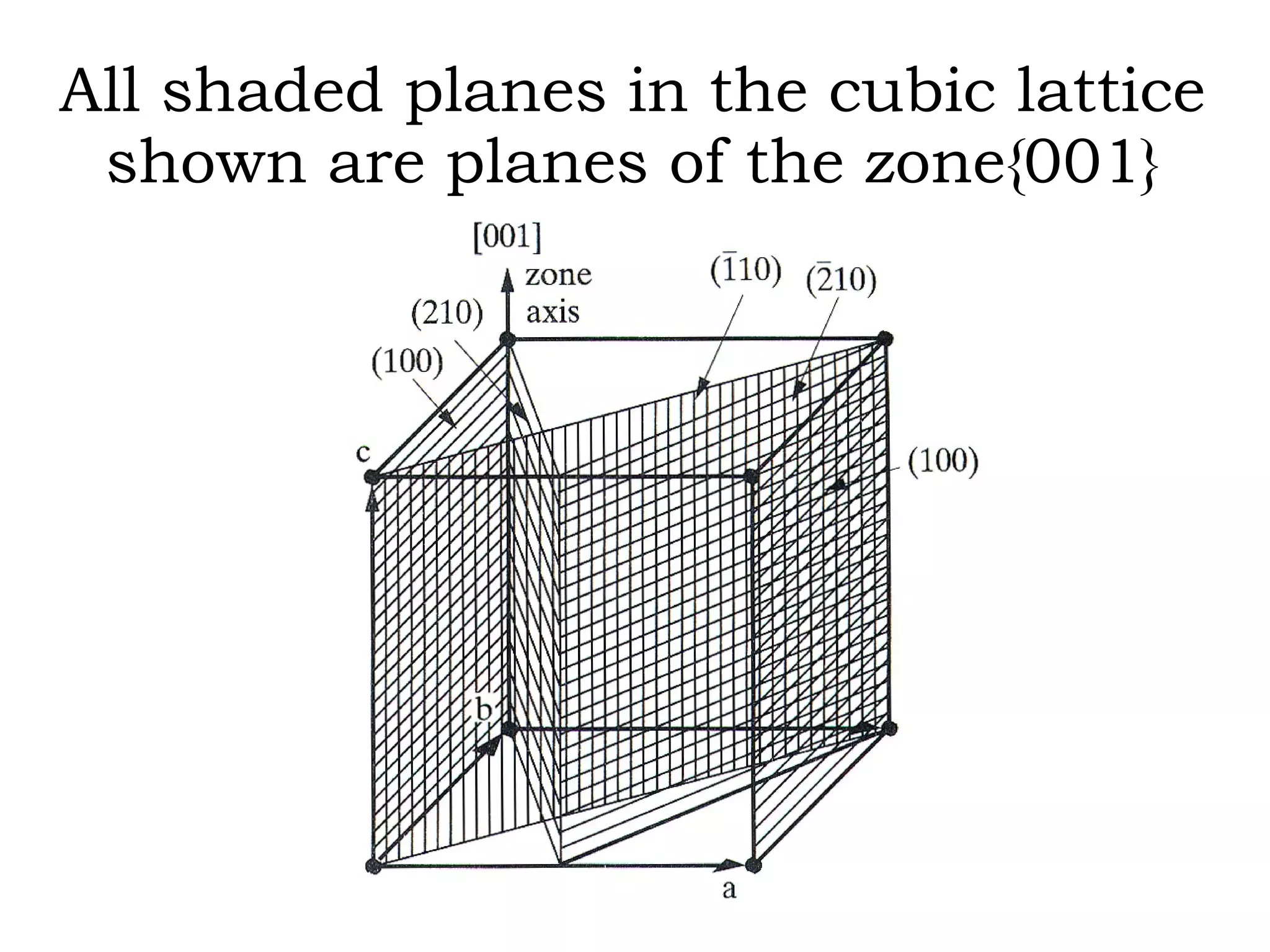
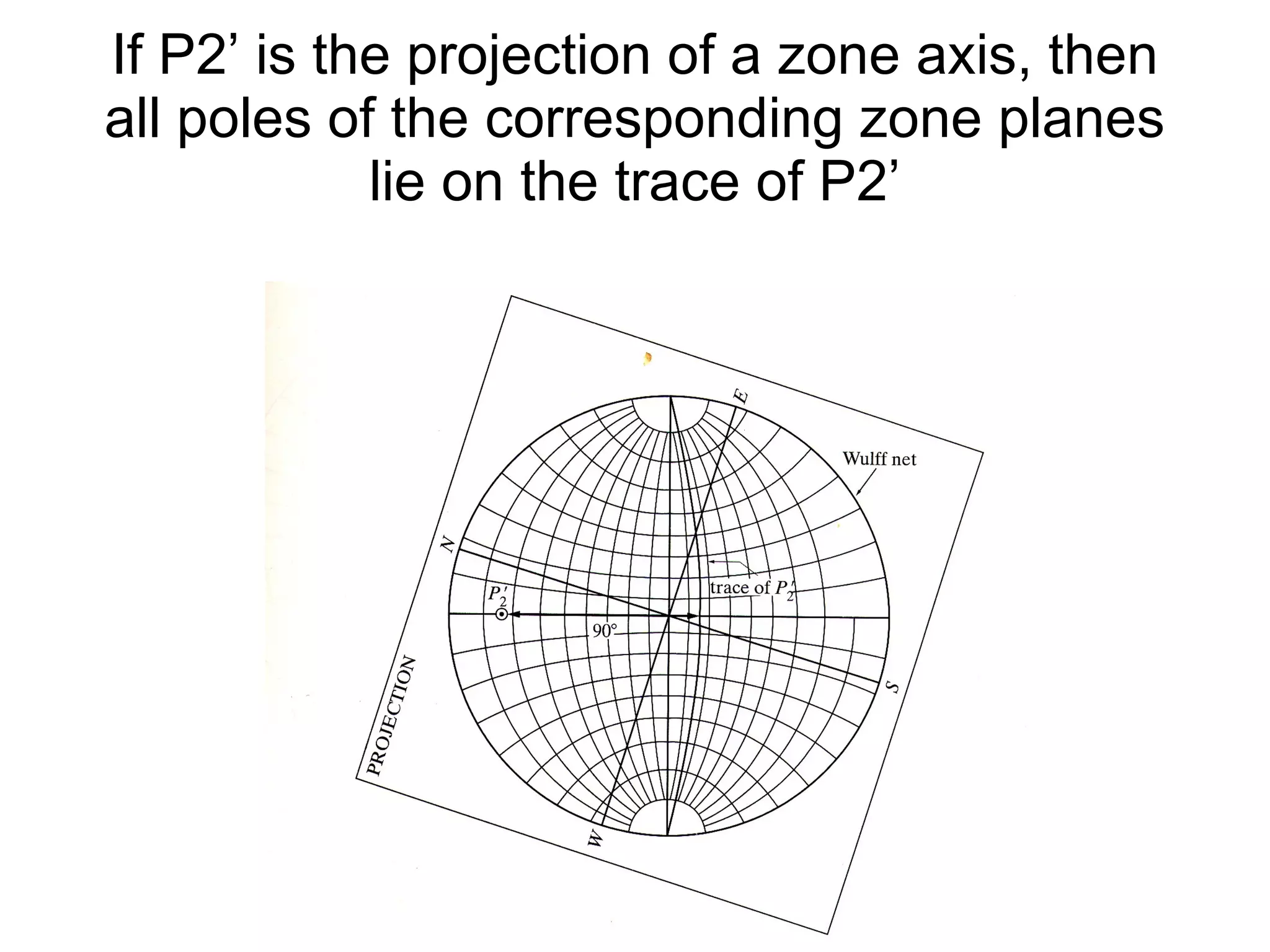
31. Zone axis [uvw] Zone plane (hkl) then hu+kv+wl=0 Two zone planes (h 1 k 1 l 1 ) and (h 2 k 2 l 2 ) then zone axis [uvw]=

32. Plane spacing

33. Indexing the hexagonal system

34. Indexing the hexagonal system

35. Crystal structure  -Fe, Cr, Mo, V  -Fe, Cu, Pb, Ni

36. Hexagonal close-packed Zn, Mg, Be,  -Ti

37. FCC and HCP

38.  -Uranium, base-centered orthorhombic (C-centered) y=0.105±0.005

43. AuBe: Simple cubic u = 0.100 w = 0.406

44. Structure of solid solution (a) Mo in Cr (substitutional) (b) C in  -Fe (interstitial)

45. Atom sizes (d) and coordination

46. Change in coordination 12  8 12  6 12  4 size contraction, percent 3 3 12

47. A: Octahedral site, B: Tetrahedral site

48. Twin

49. (a) (b) FCC annealing (c) HCP deformation twins

50. Twin band in FCC lattice, Plane of main drawing is (1 ī 0)

51. Homework assignment Problem 2-6 Problem 2-8 Problem 2-9 Problem 2-10

52. Stereographic projection *Any plane passing the center of the reference sphere intersects the sphere in a trace called great circle * A plane can be represented by its great circle or pole, which is the intersection of its plane normal with the reference sphere

53. Stereographic projection

55. Pole on upper sphere can also be projected to the horizontal (equatorial) plane

56. Projections of the two ends of a line or plane normal on the equatorial plane are symmetrical with respect to the center O.

57. Projections of the two ends of a line or plane normal on the equatorial plane are symmetrical with respect to the center O. U L P P’ P P’ X O O

58. A great circle representing a plane is divided to two half circles, one in upper reference sphere, the other in lower sphere Each half circle is projected as a trace on the equatorial plane The two traces are symmetrical with respect to their associated common diameter

59. N S E W

60. The position of pole P can be defined by two angles  and 

61. The position of projection P’ can be obtained by r = R tan(  /2)

62. The trace of each semi-great circle hinged along NS projects on WNES plane as a meridian

63. As the semi-great circle swings along NS, the end point of each radius draws on the upper sphere a curve which projects on WNES plane as a parallel

64. The weaving of meridians and parallels makes the Wulff net

65. Two projected poles can always be rotated along the net normal to a same meridian (not parallel) such that their intersecting angle can be counted from the net

66. P : a pole at (  1 ,  1 ) NMS : its trace

67. The projection of a plane trace and pole can be found from each other by rotating the projection along net normal to the following position

68. Zone circle and zone pole

69. If P2’ is the projection of a zone axis, then all poles of the corresponding zone planes lie on the trace of P2’

70. Rotation of a poles about NS axis by a fixed angle: the corresponding poles moving along a parallel *Pole A1 move to pole A2 *Pole B1 moves 40 ° to the net end then another 20 ° along the same parallel to B1’ corresponding to a movement on the lower half reference sphere, pole corresponding to B1’ on upper half sphere is B2

71. m: mirror plane F1: face 1 F2: face 2 N1: normal of F1 N2: normal of N2 N1, N2 lie on a plane which is 丄 to m

73. A plane not passing through the center of the reference sphere intersects the sphere on a small circle which also projects as a circle, but the center of the former circle does not project as the center of the latter.

74. Projection of a small circle centered at Y

75. Rotation of a pole A1 along an inclined axis B1: B1  B3  B2  B2  B3  B1 A1  A1  A2  A3  A4  A4 A plane not passing through the center of the reference sphere intersects the sphere on a small circle which also projects as a circle .

76. Rotation of a pole A1 along an inclined axis B1:

77. A 1 rotate about B 1 forming a small circle in the reference sphere, the small circle projects along A 1 , A 4 , D, arc A 1 , A 4 , D centers around C (not B 1 ) in the projection plane

78. Rotation of 3 directions along b axis

79. Rotation of 3 directions along b axis

80. Rotation of 3 directions along b axis

81. Standard coordinates for crystal axes

82. Standard coordinates for crystal axes

83. Standard coordinates for crystal axes

84. Standard coordinates for crystal axes

85. Projection of a monoclinic crystal +C -b +b -a + a x x 011 0-1-1 01-1 0-11 -110 -1-10 110 1-10

86. Projection of a monoclinic crystal

87. Projection of a monoclinic crystal

88. Projection of a monoclinic crystal

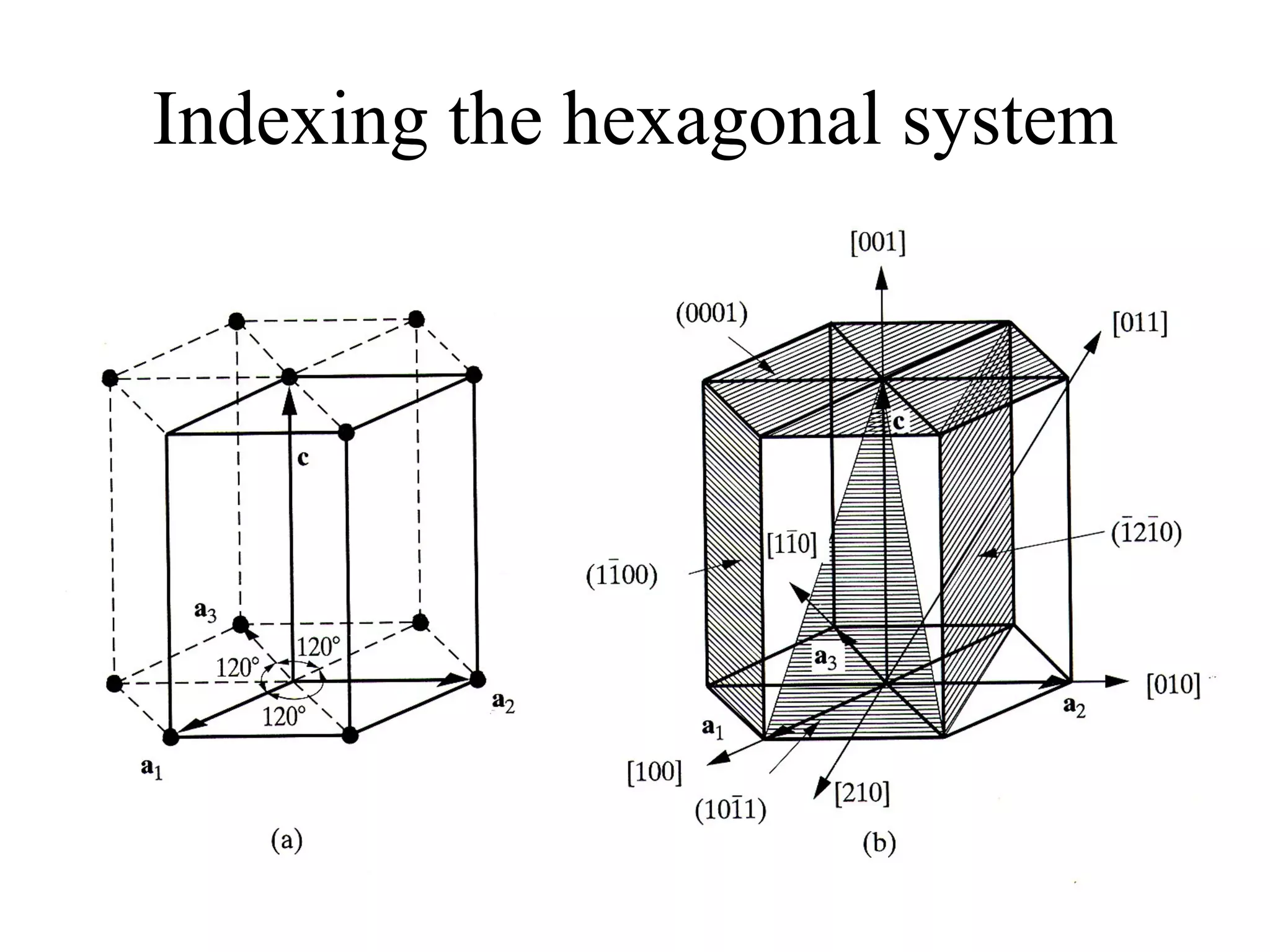
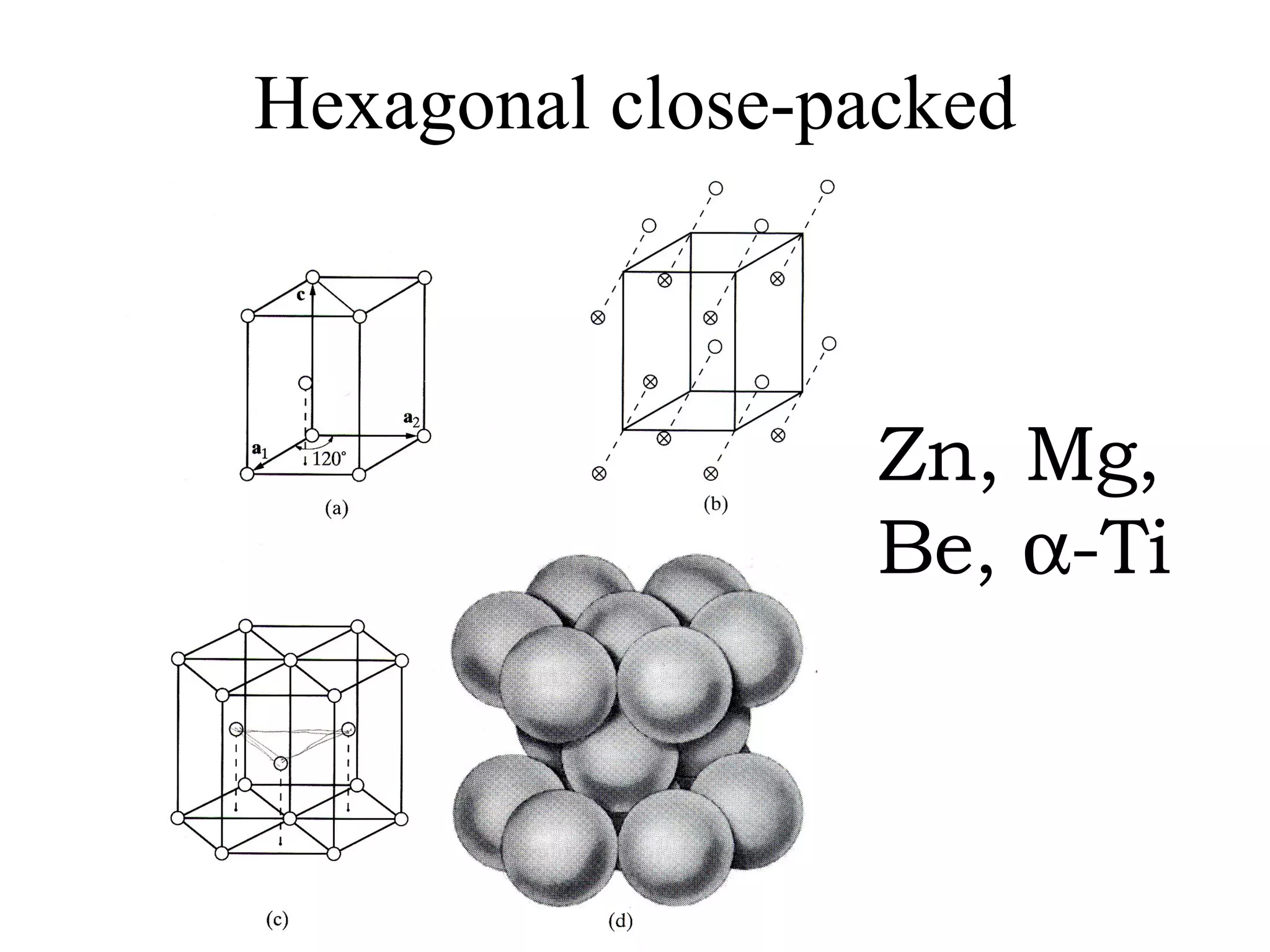
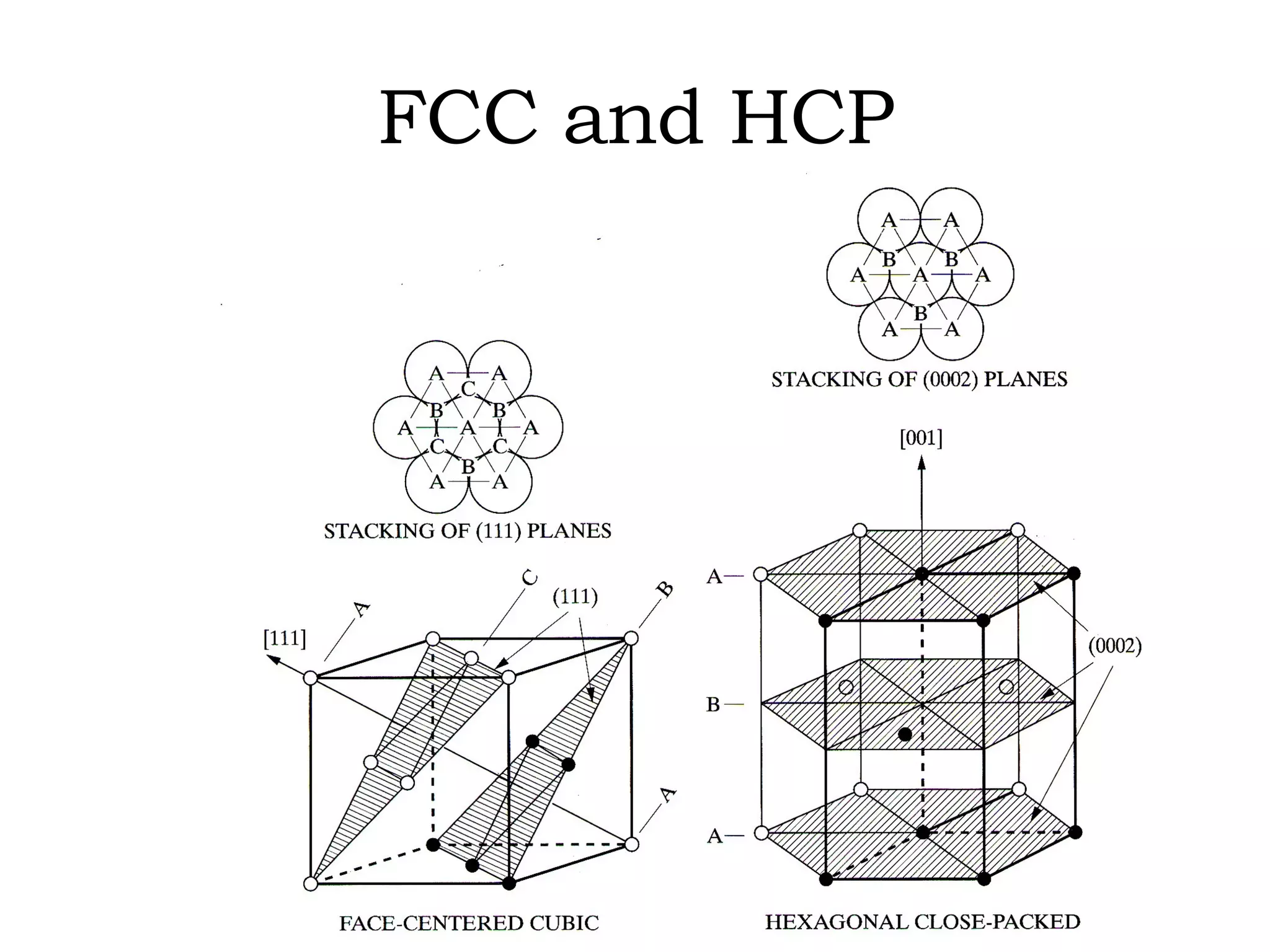
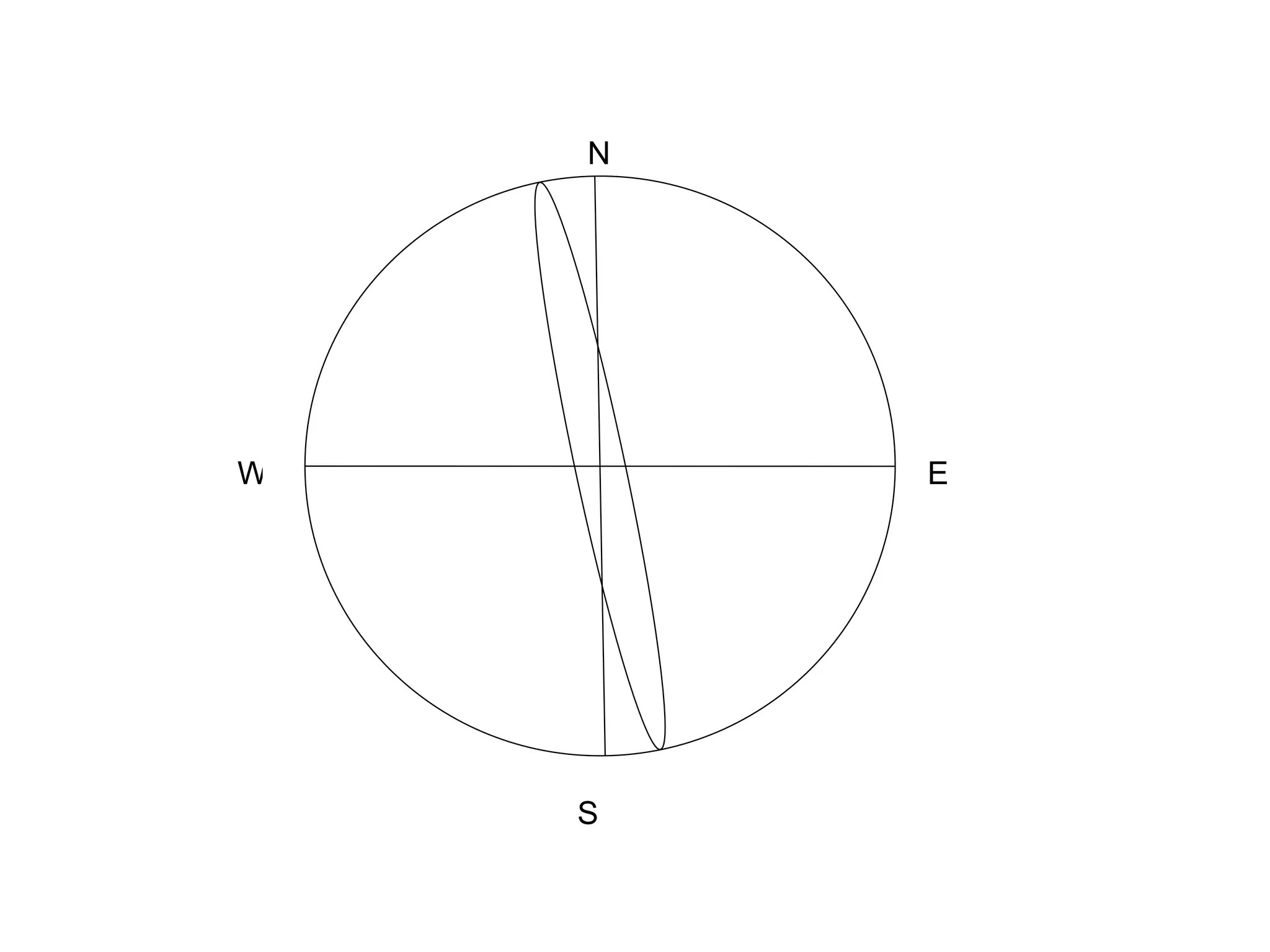
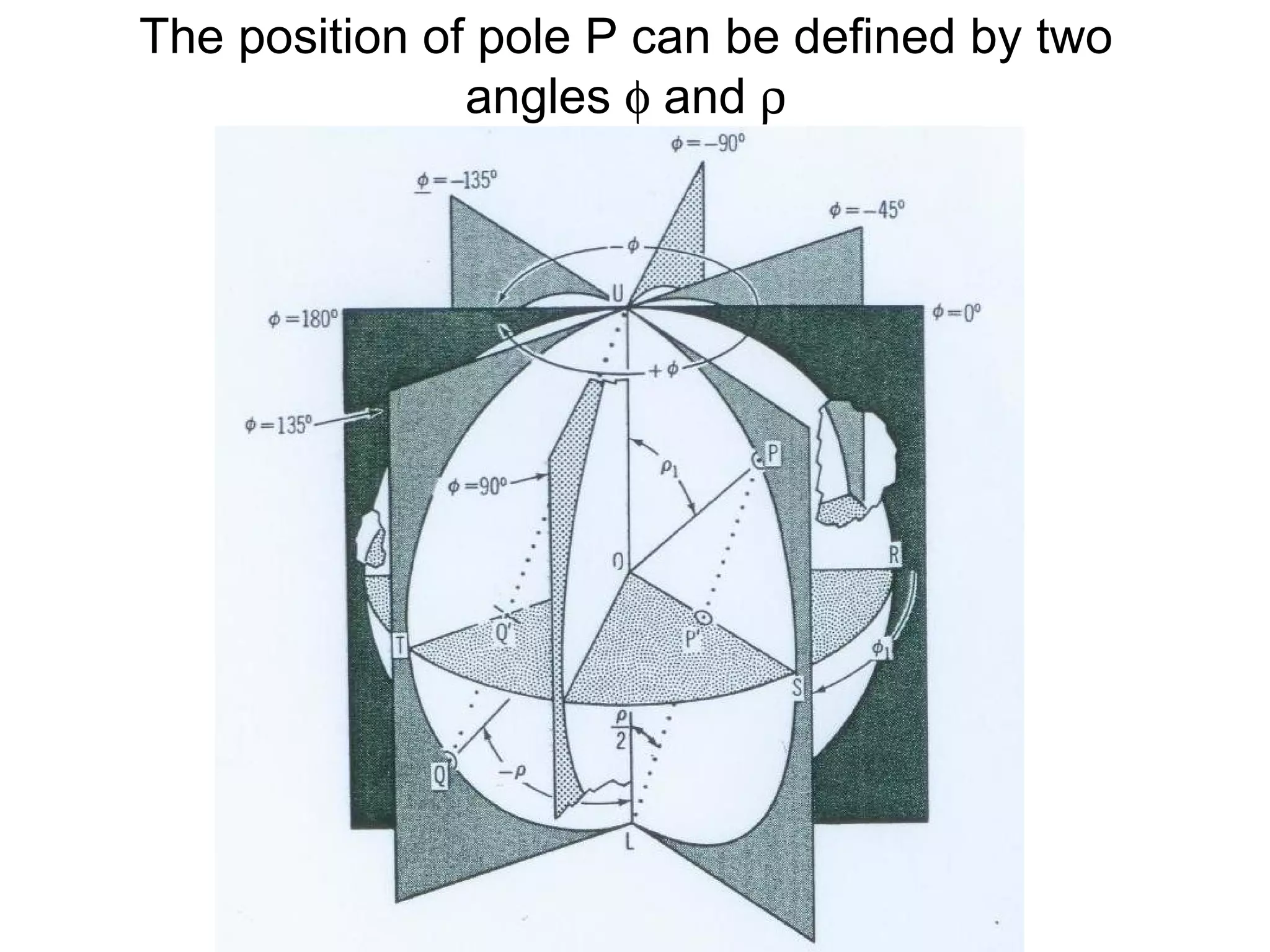
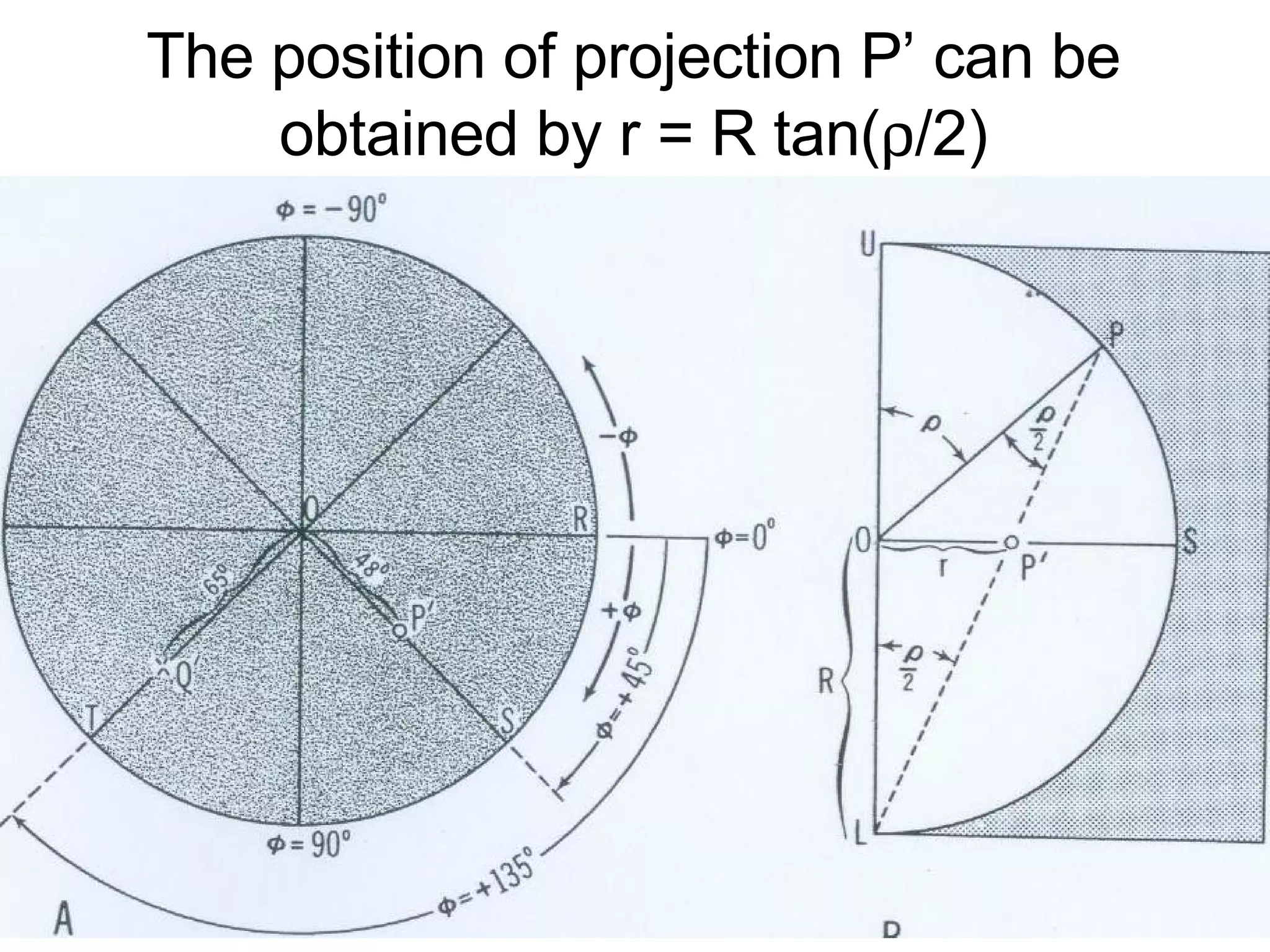
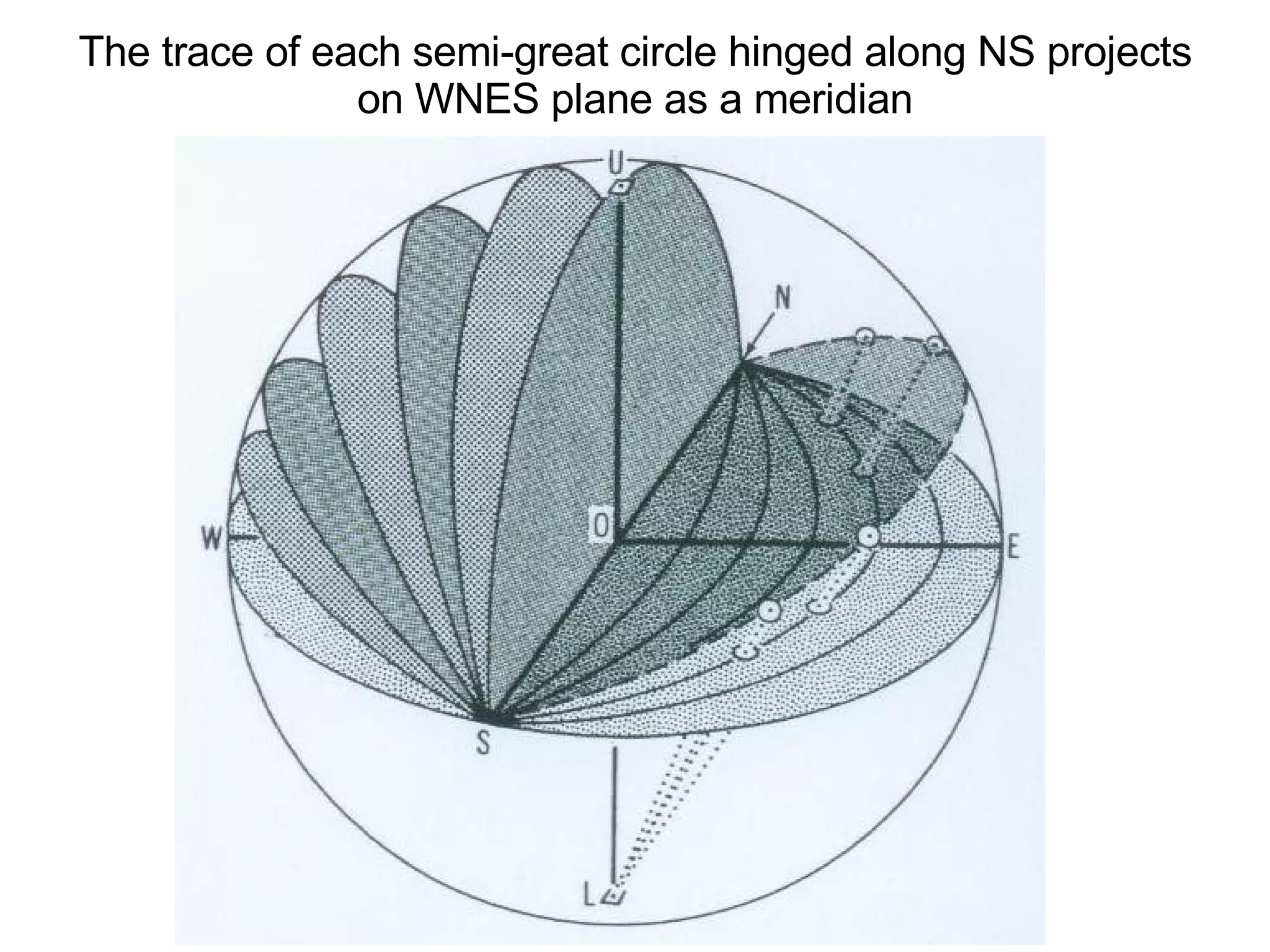
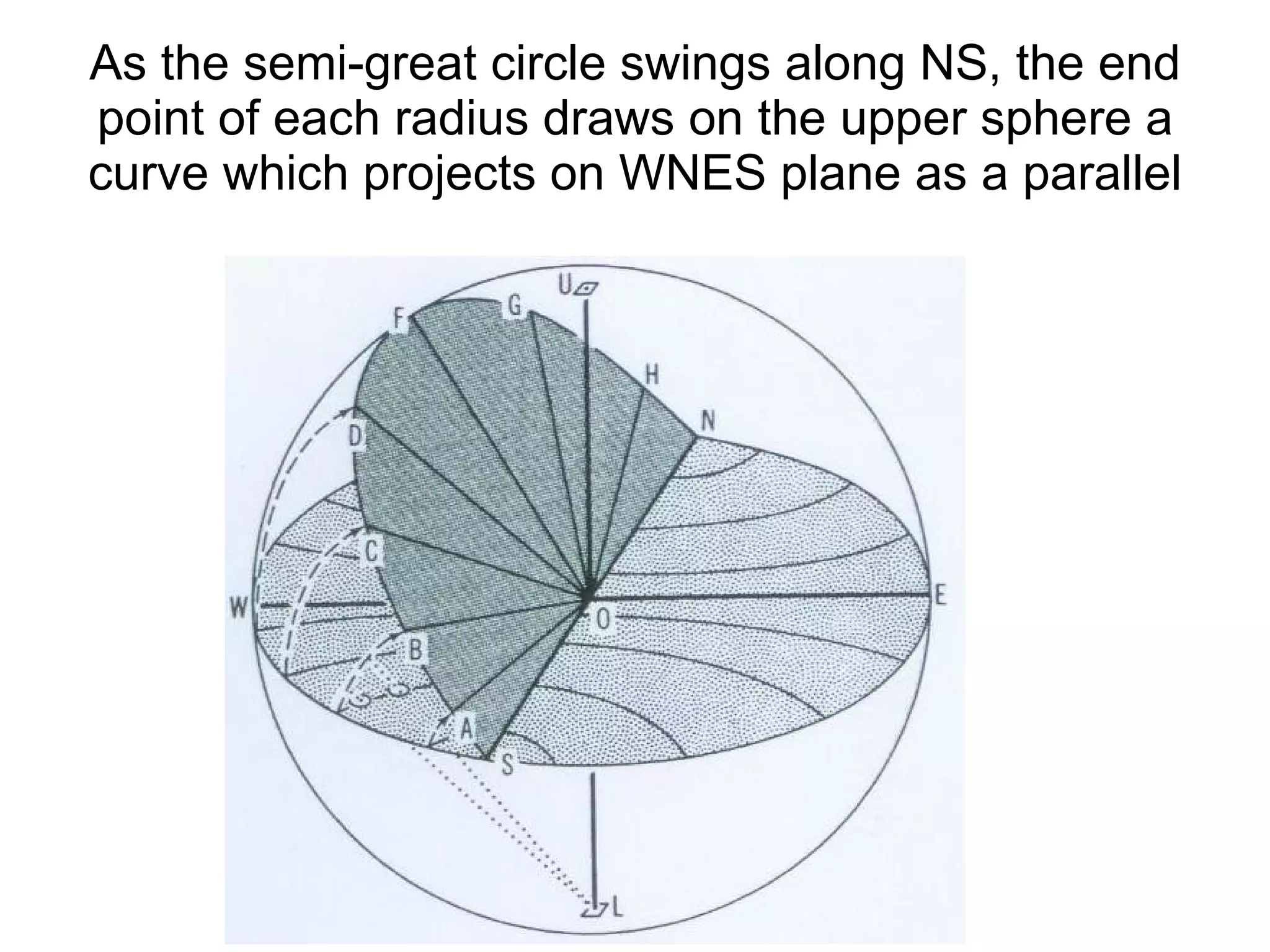
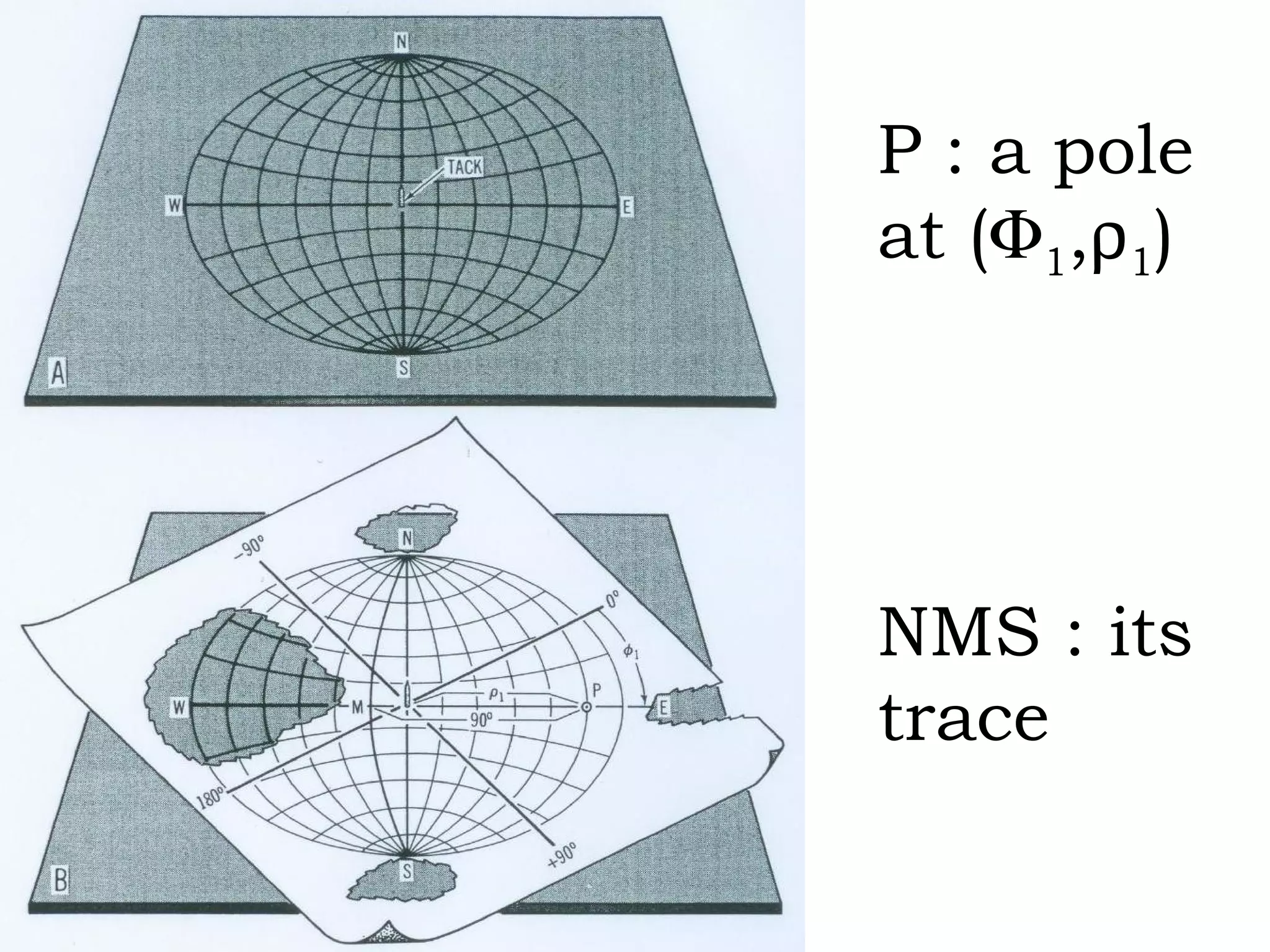
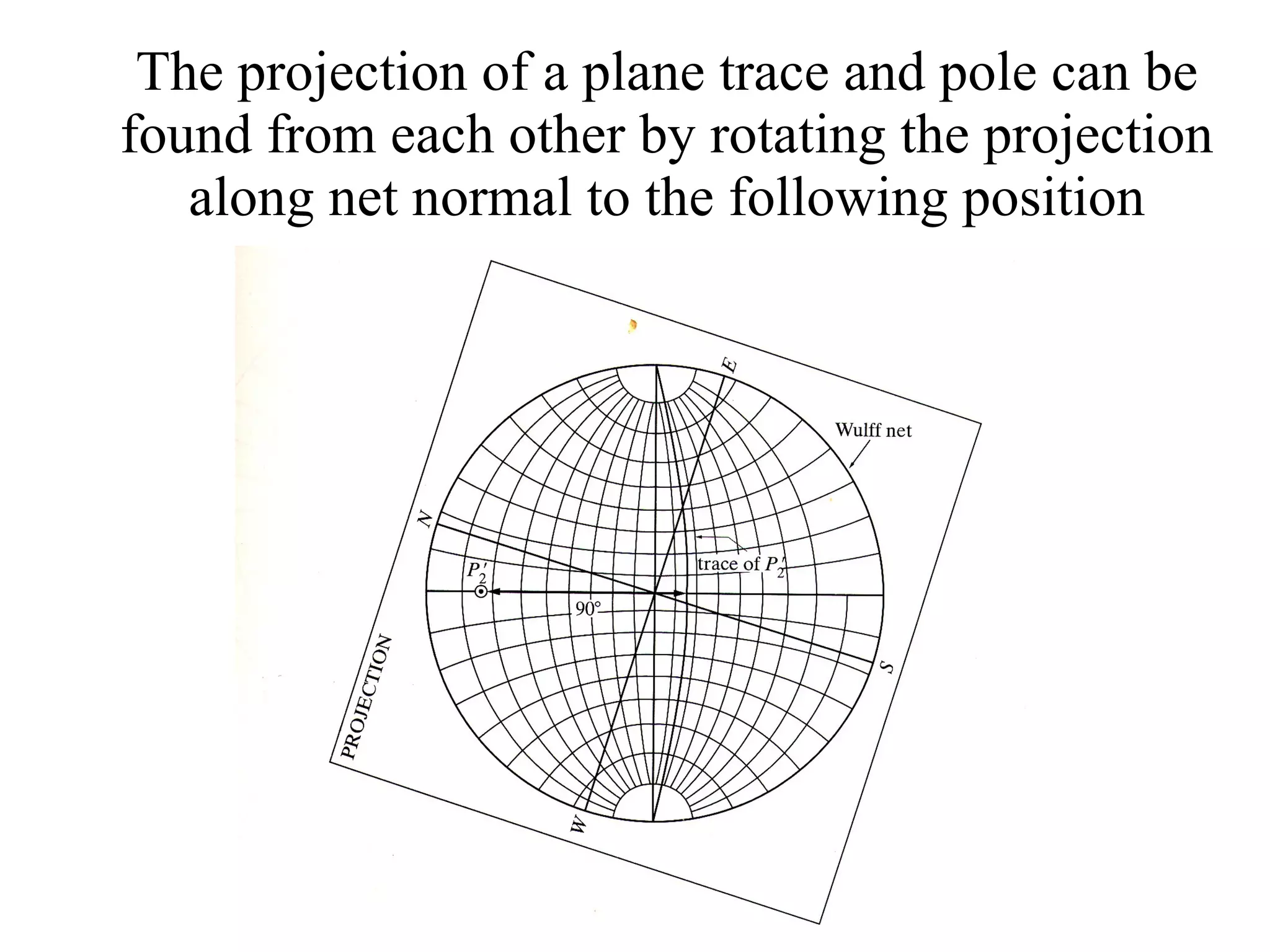
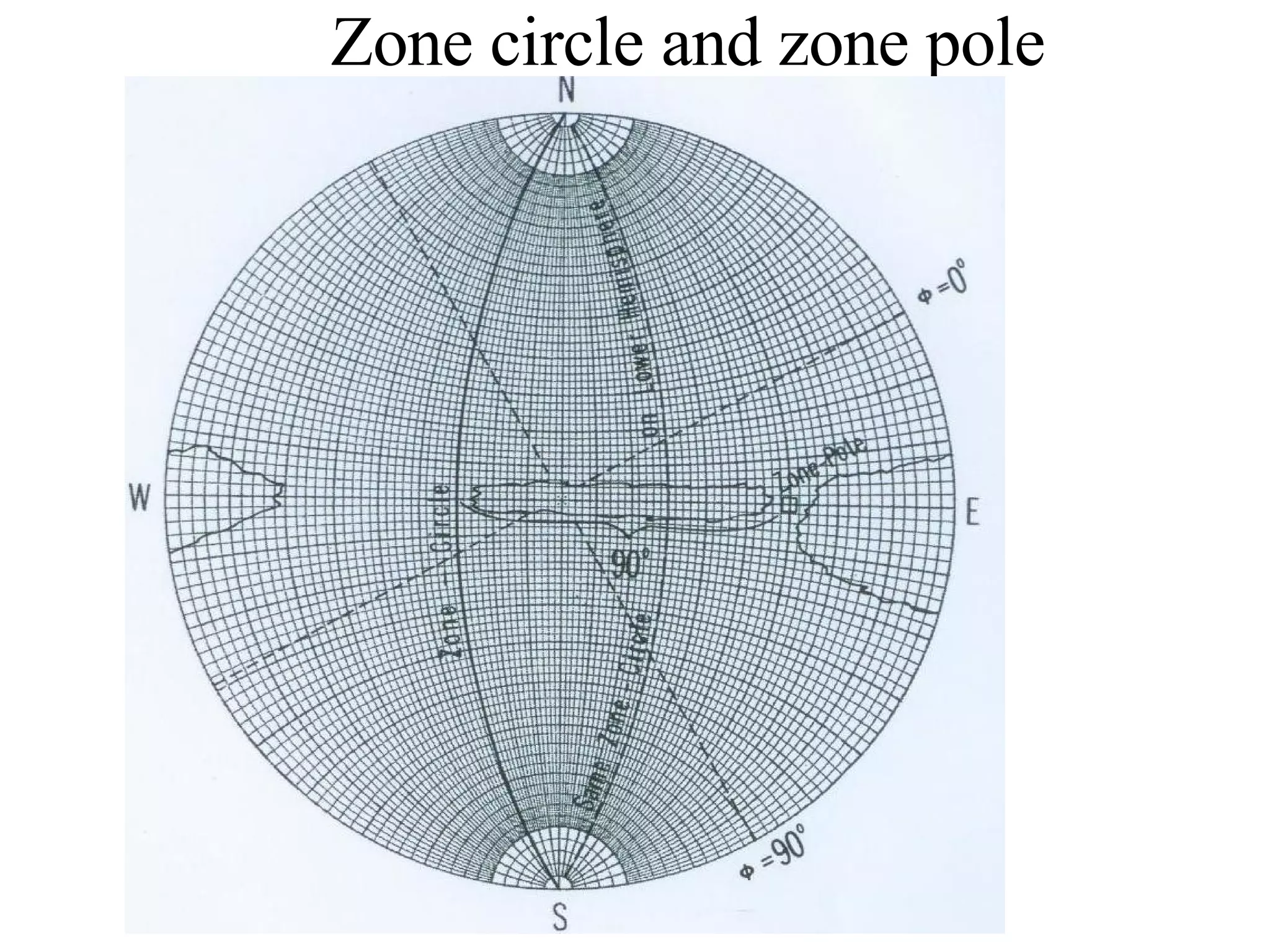
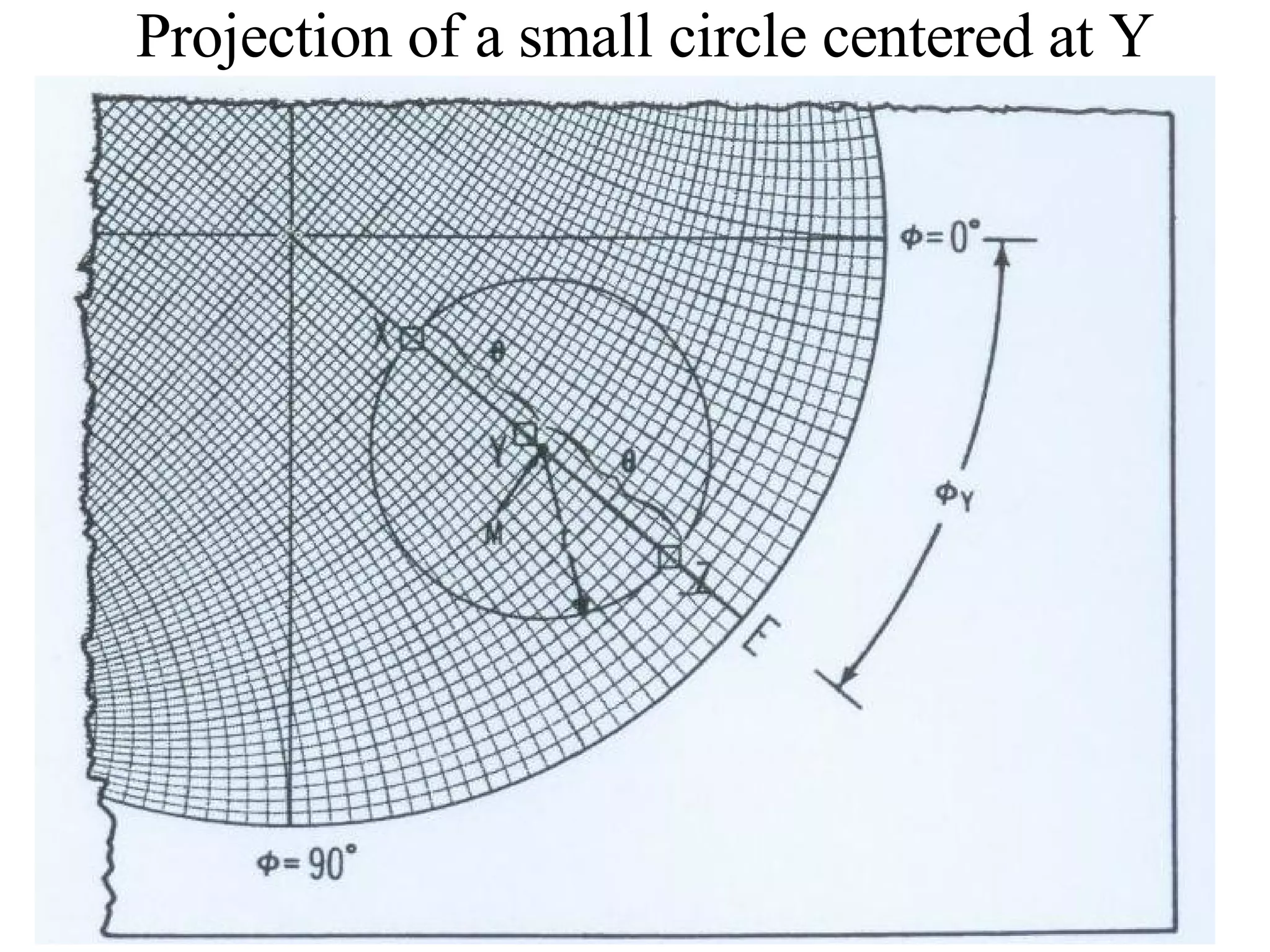
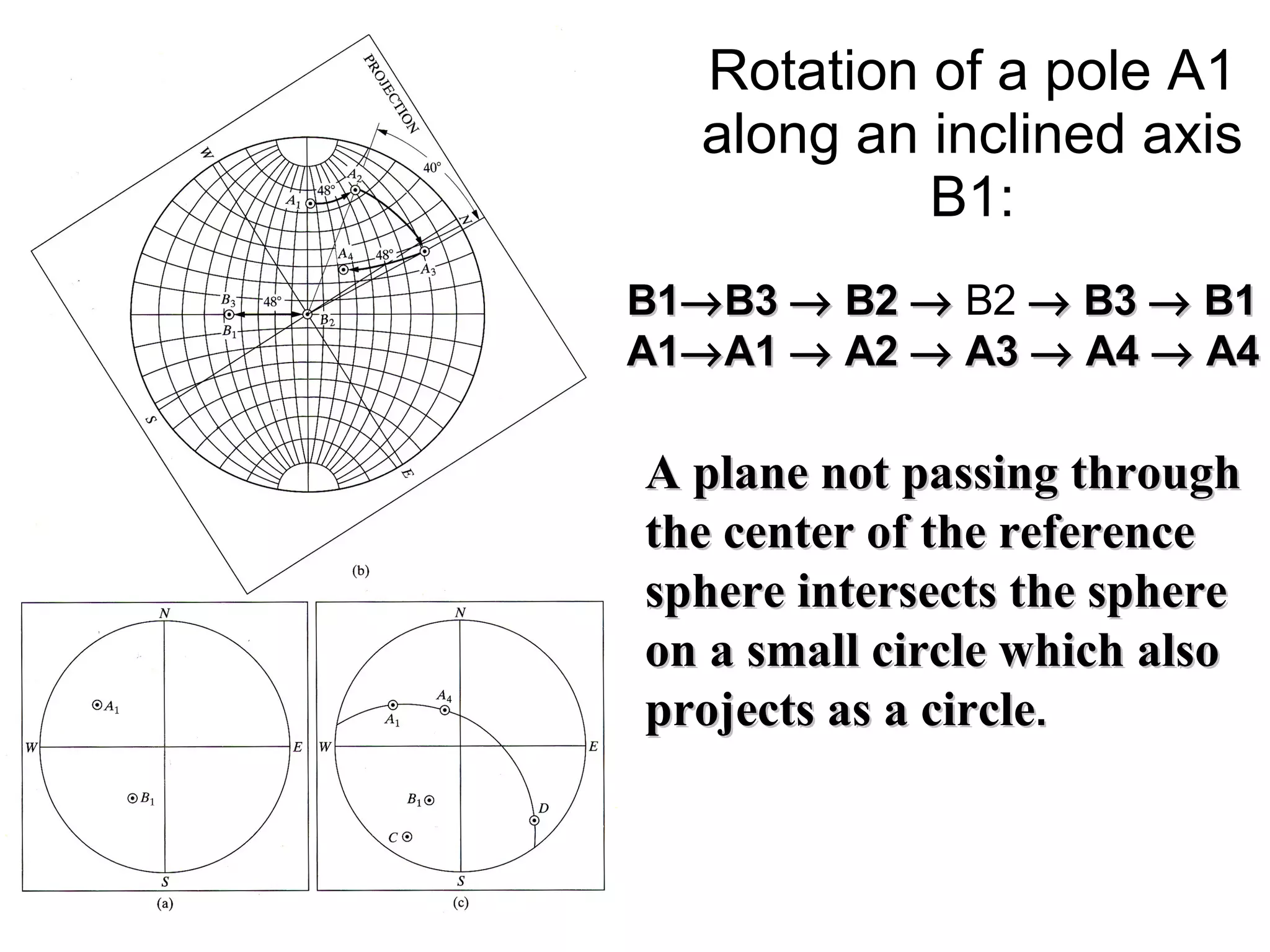
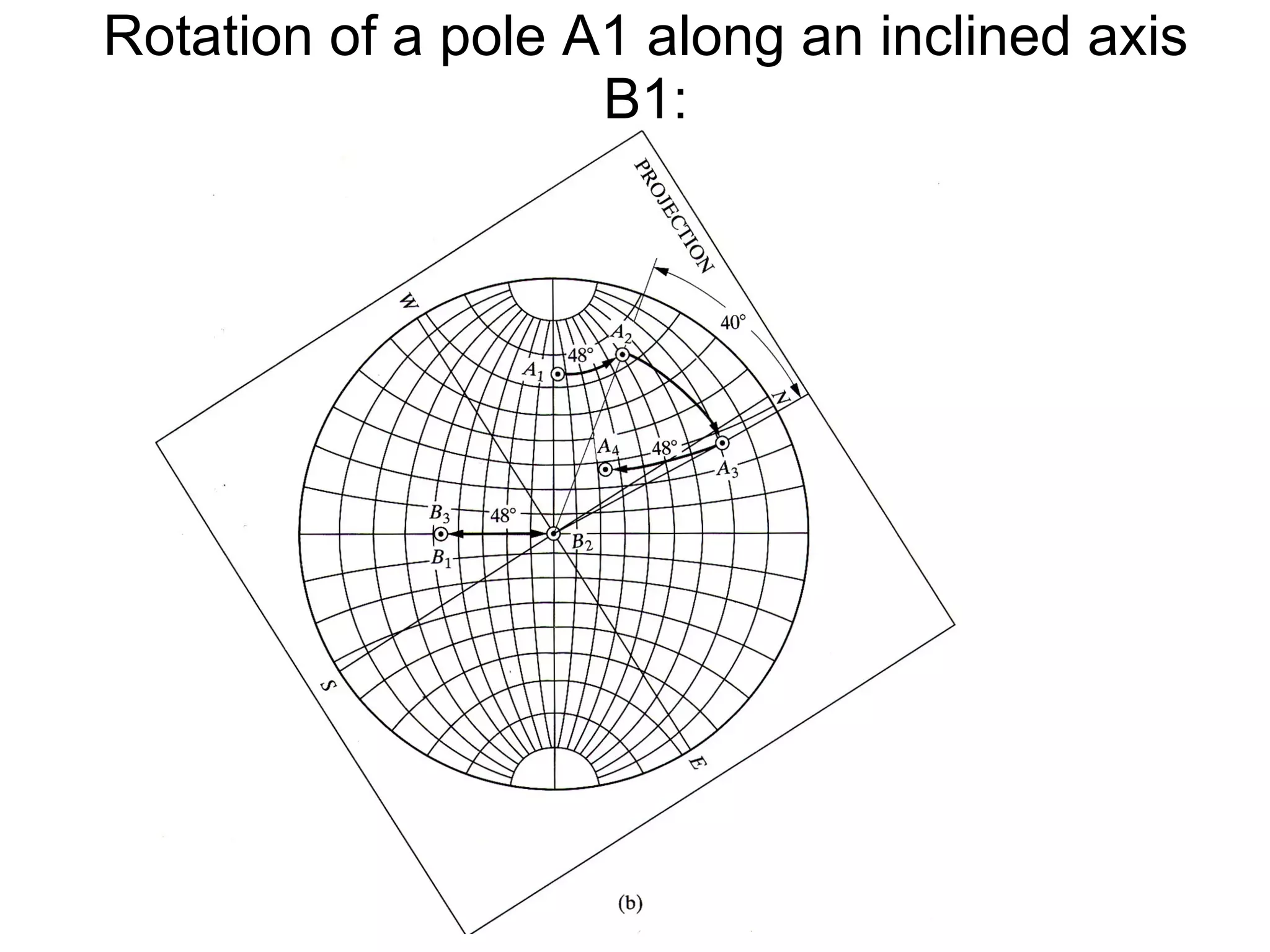
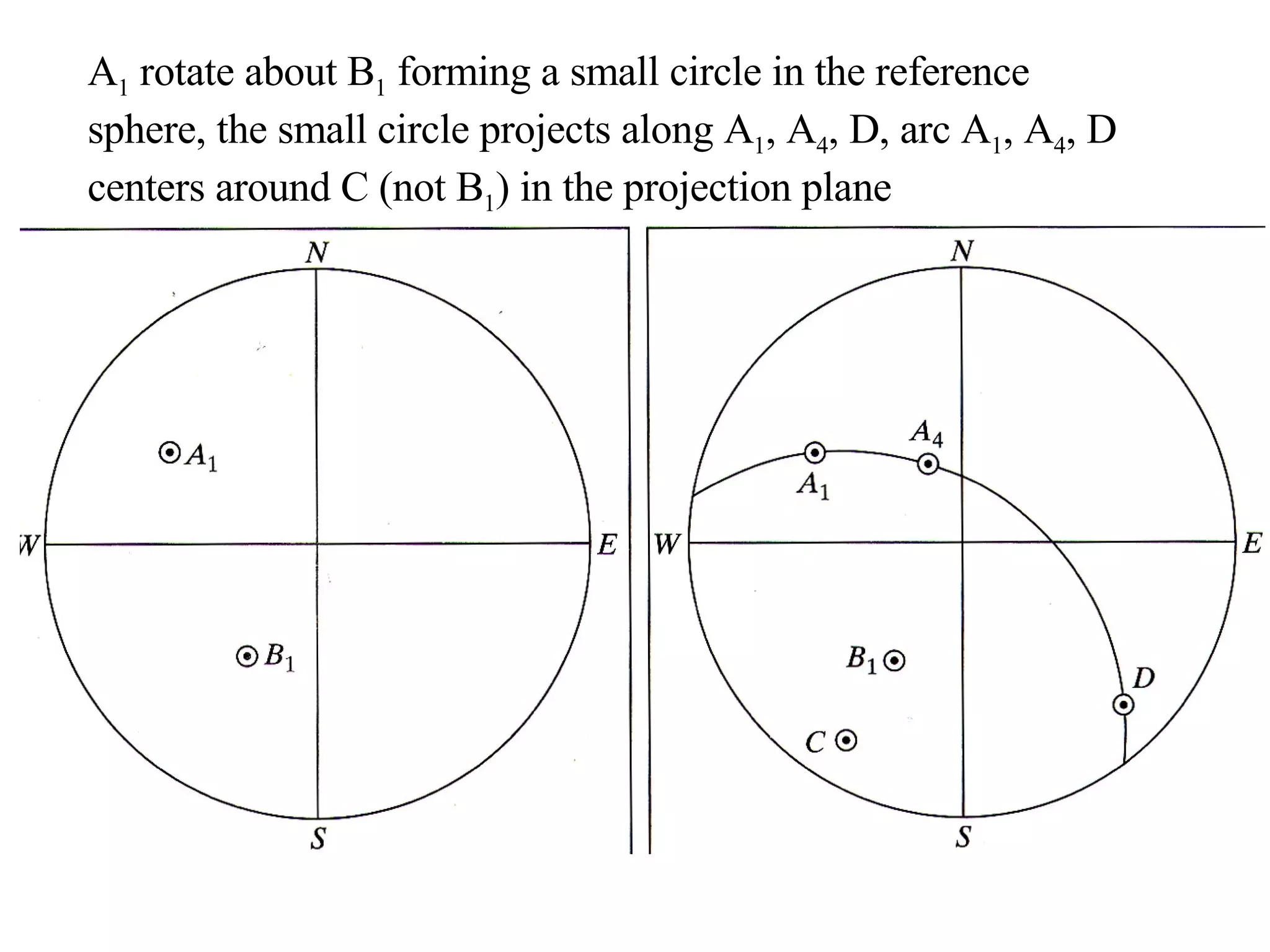
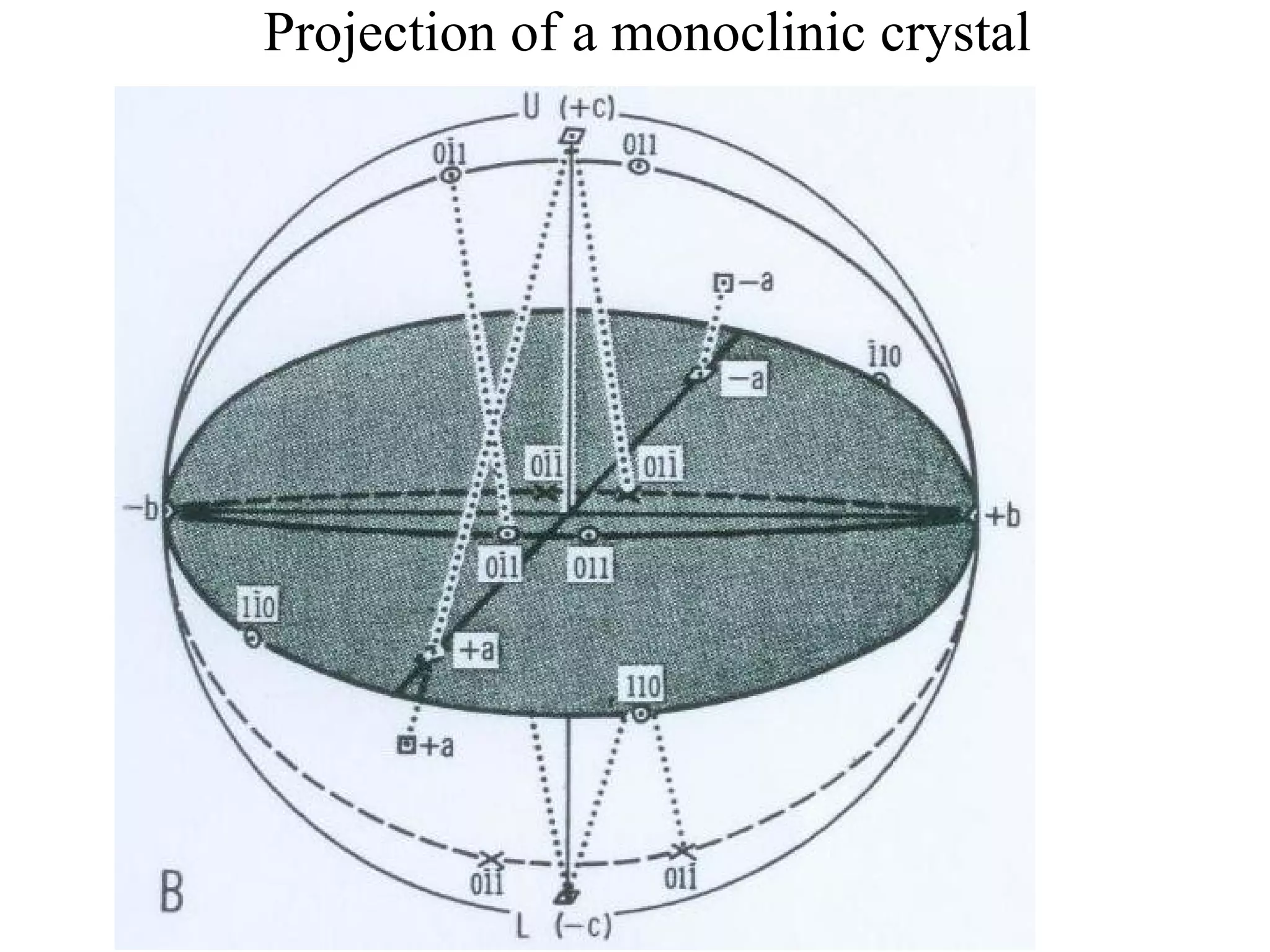
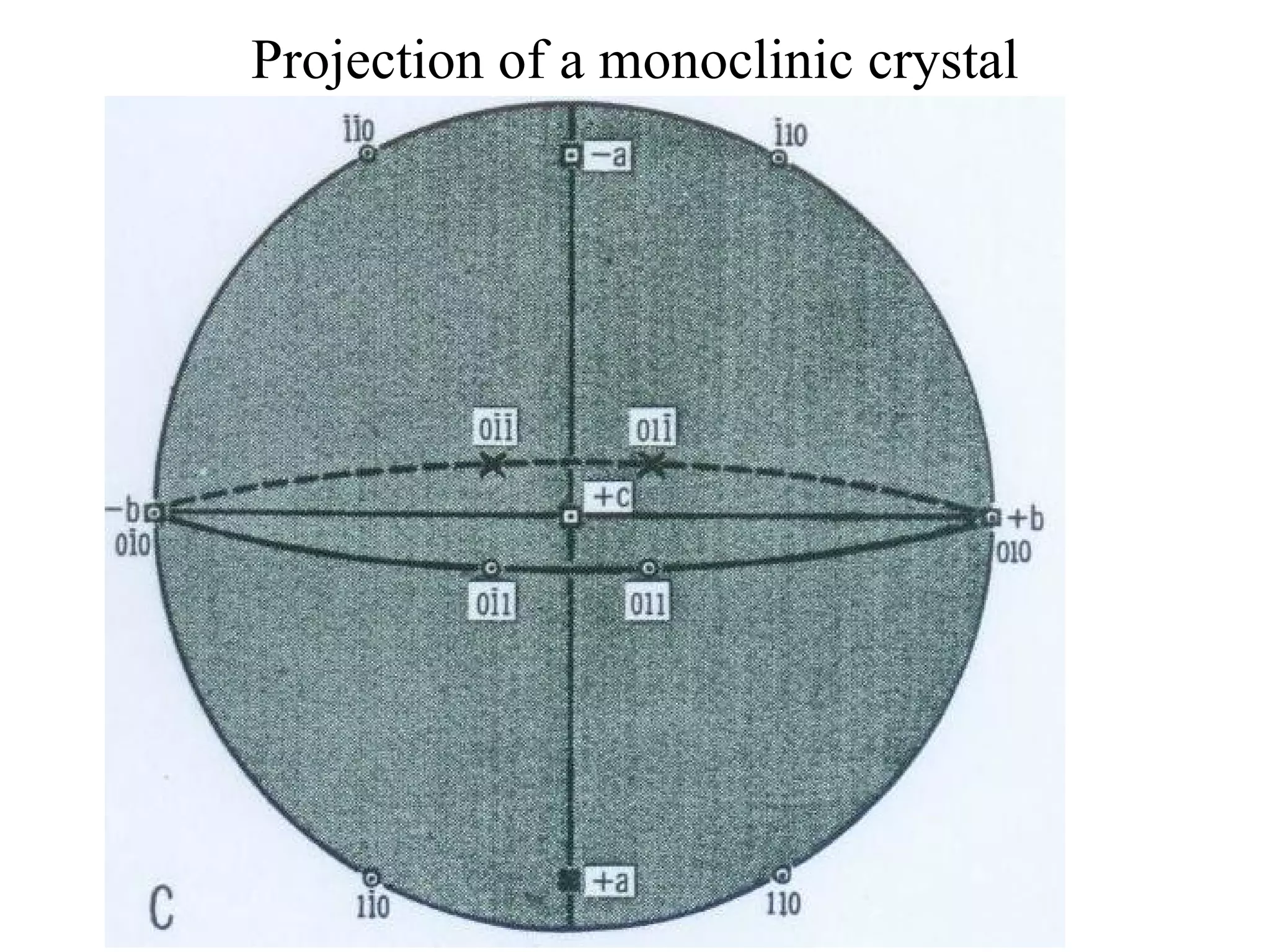
89. (a) Zone plane (stippled) (b) zone circle with zone axis ā, note [100] • [0xx]=0

90. Location of axes for a triclinic crystal: the circle on net has a radius of  along WE axis of the net

92. Zone circles corresponding to a, b, c axes of a triclinic crystal

93. Standard projections of cubic crystals on (a) (001), (b) (011)

94. d/(a/h)=cos  , d/(b/k)=cos  , d/(c/l)=cos  h:k:l=a  cos  : b  cos  : c  cos  measure 3 angles to calculate hkl

95. The face poles of six faces related by -3 axis that is (a) perpendicular (b) oblique to the plane of projection