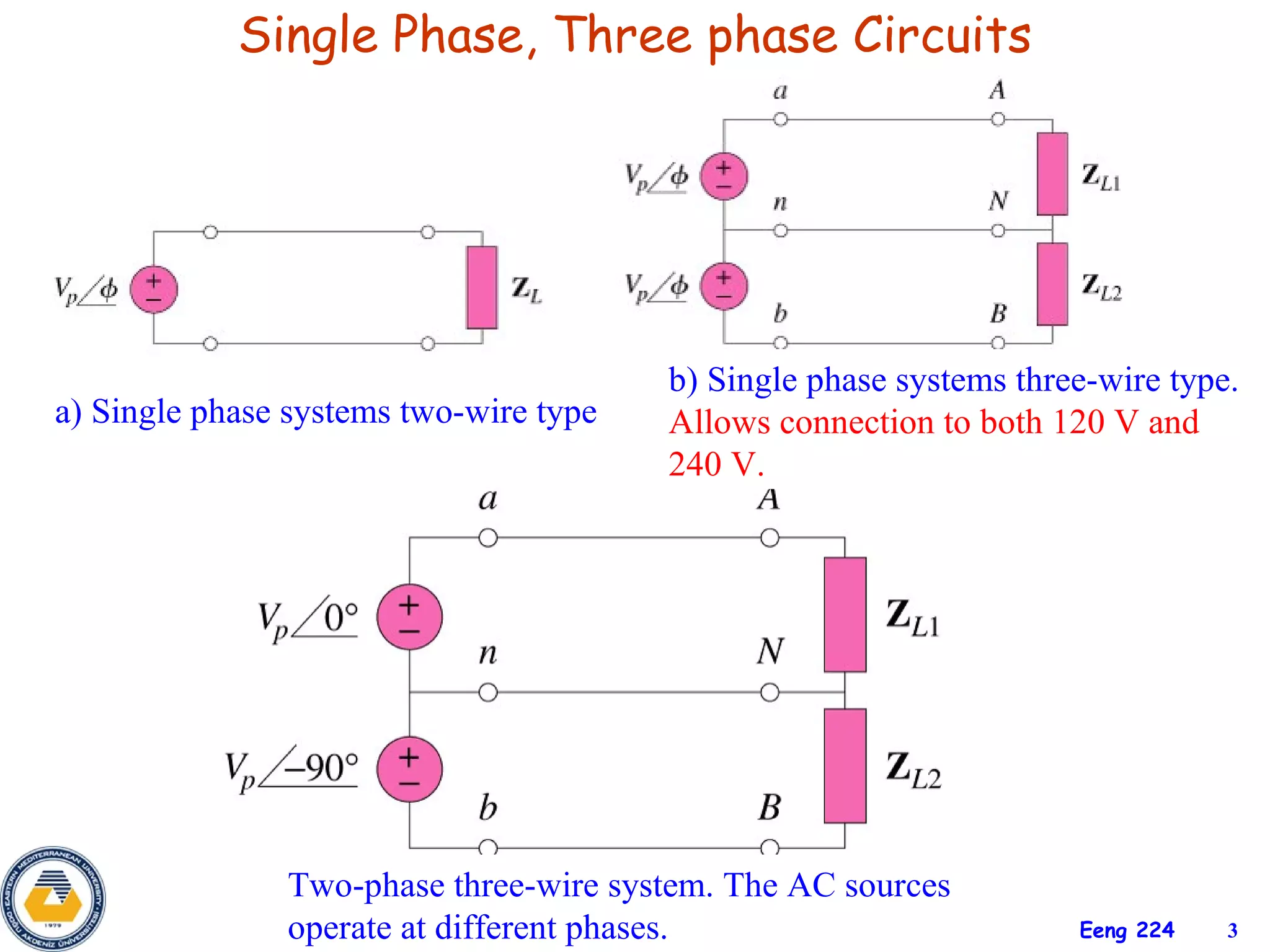
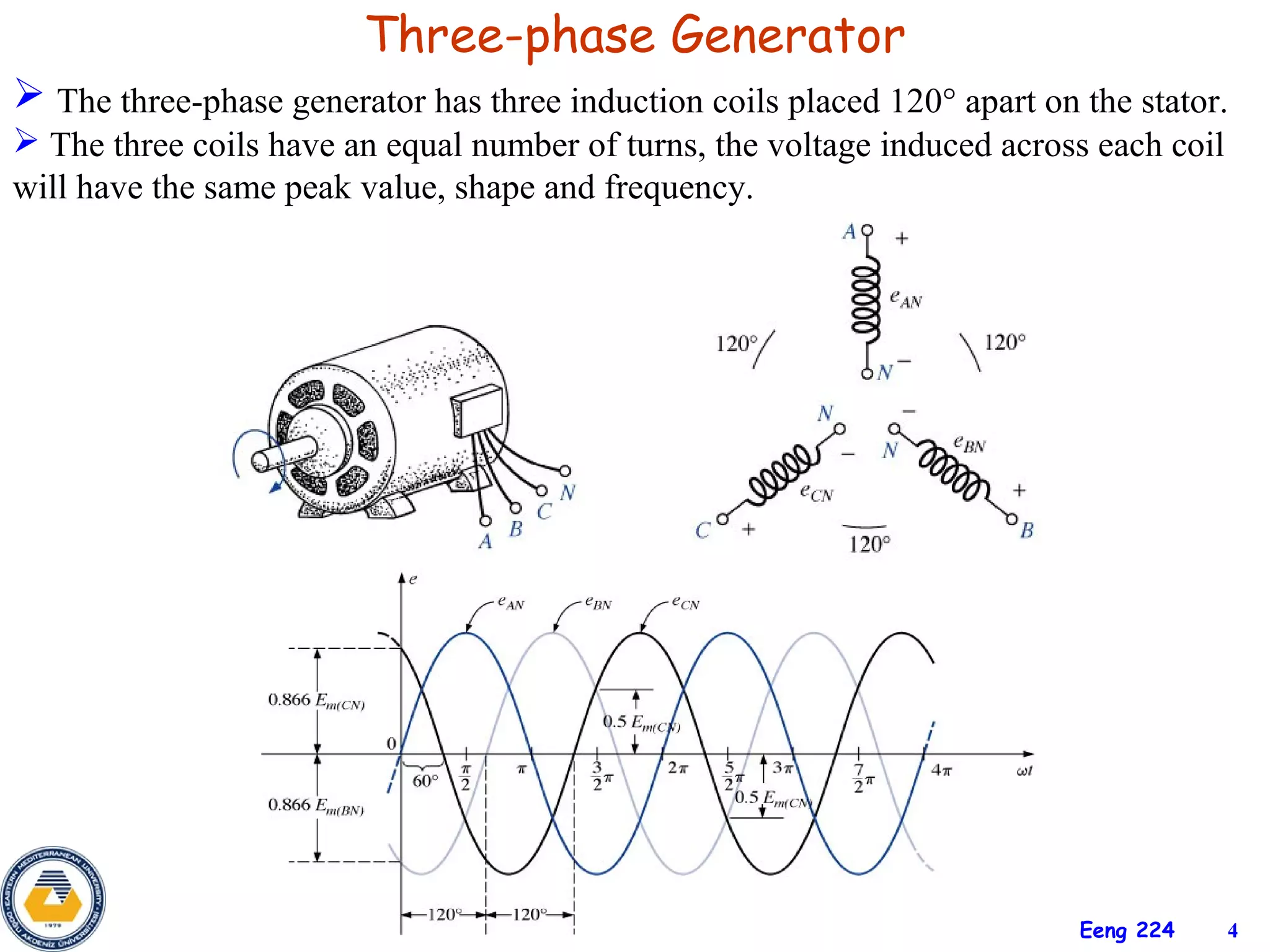
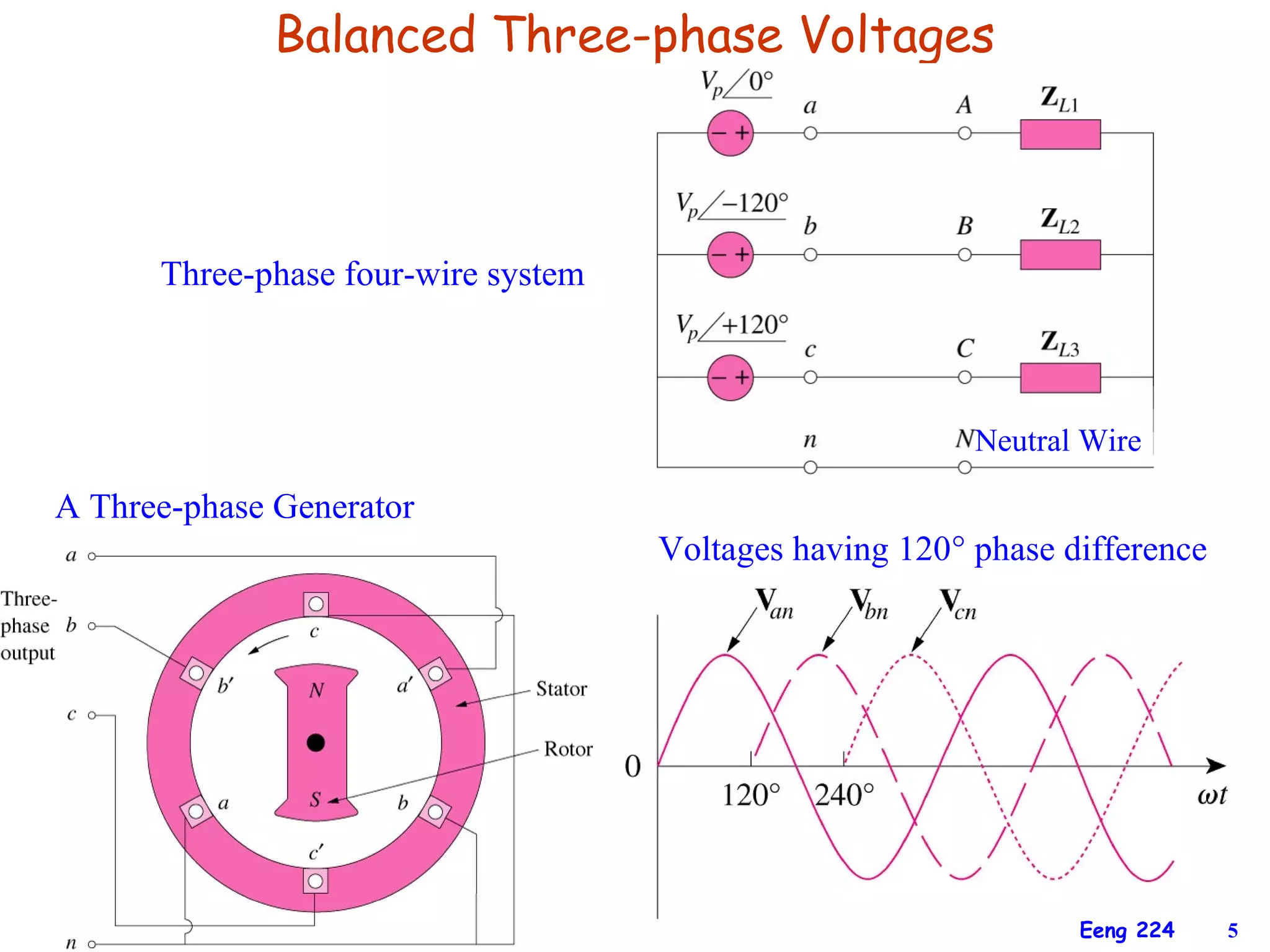
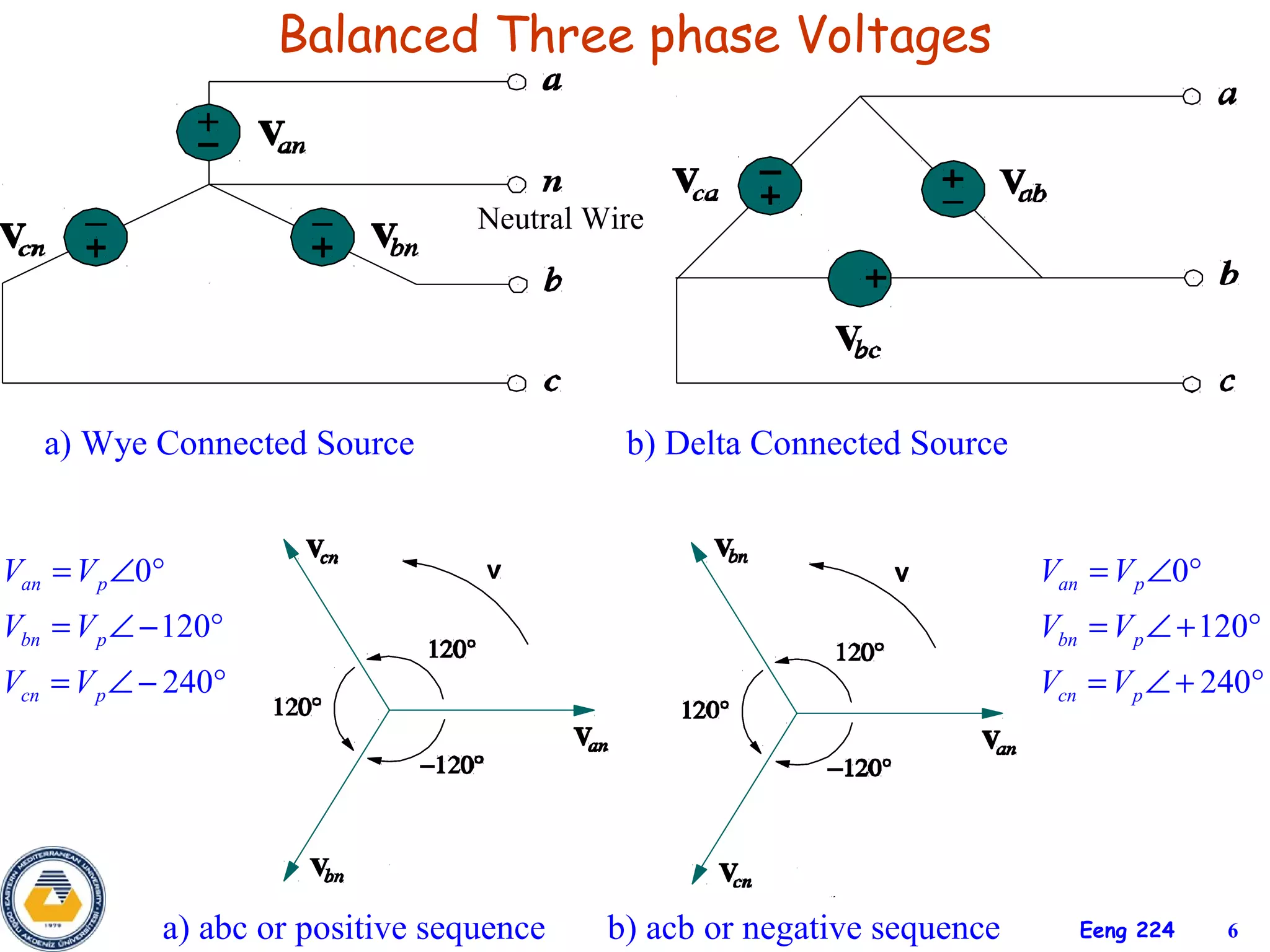
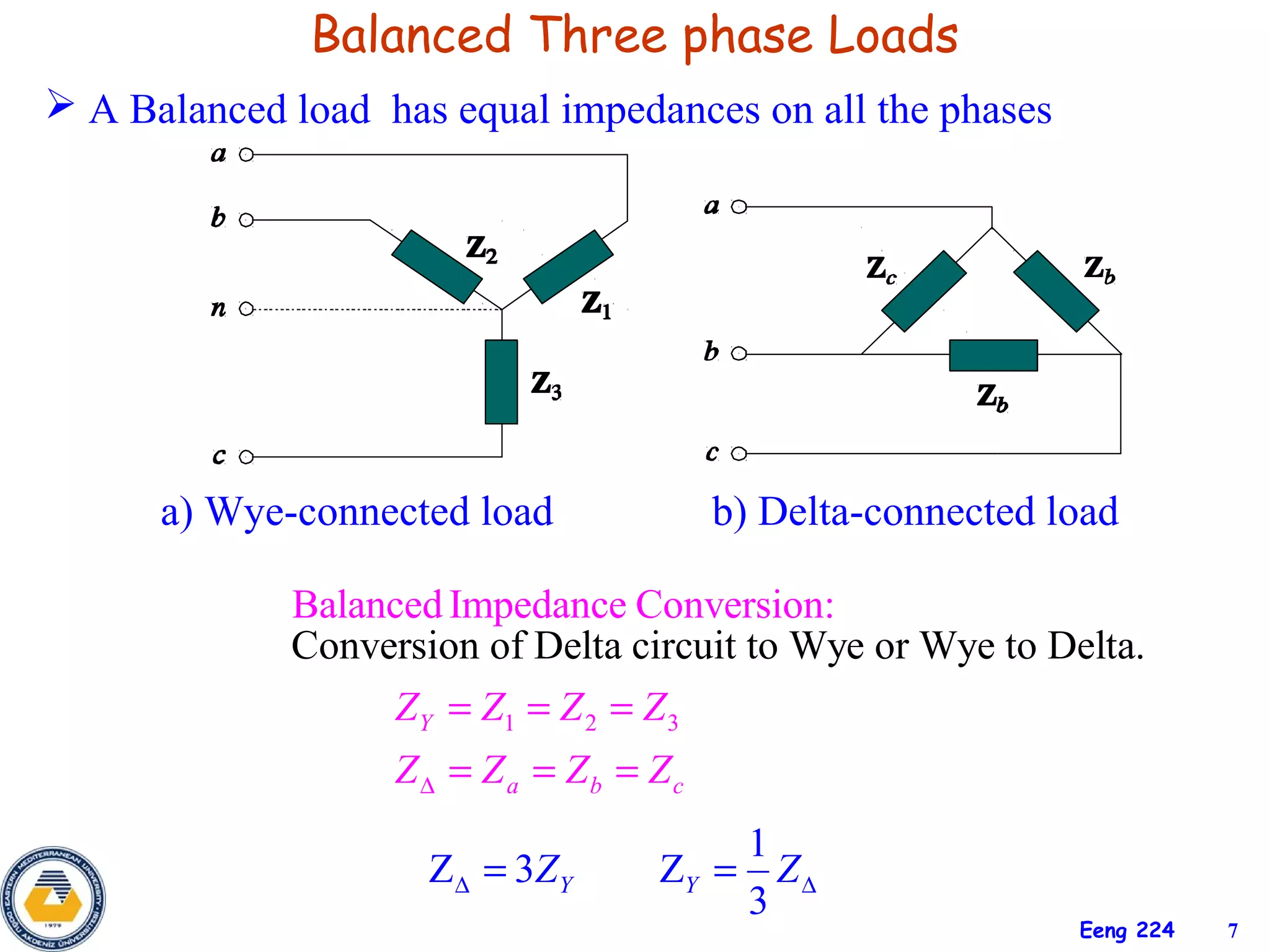
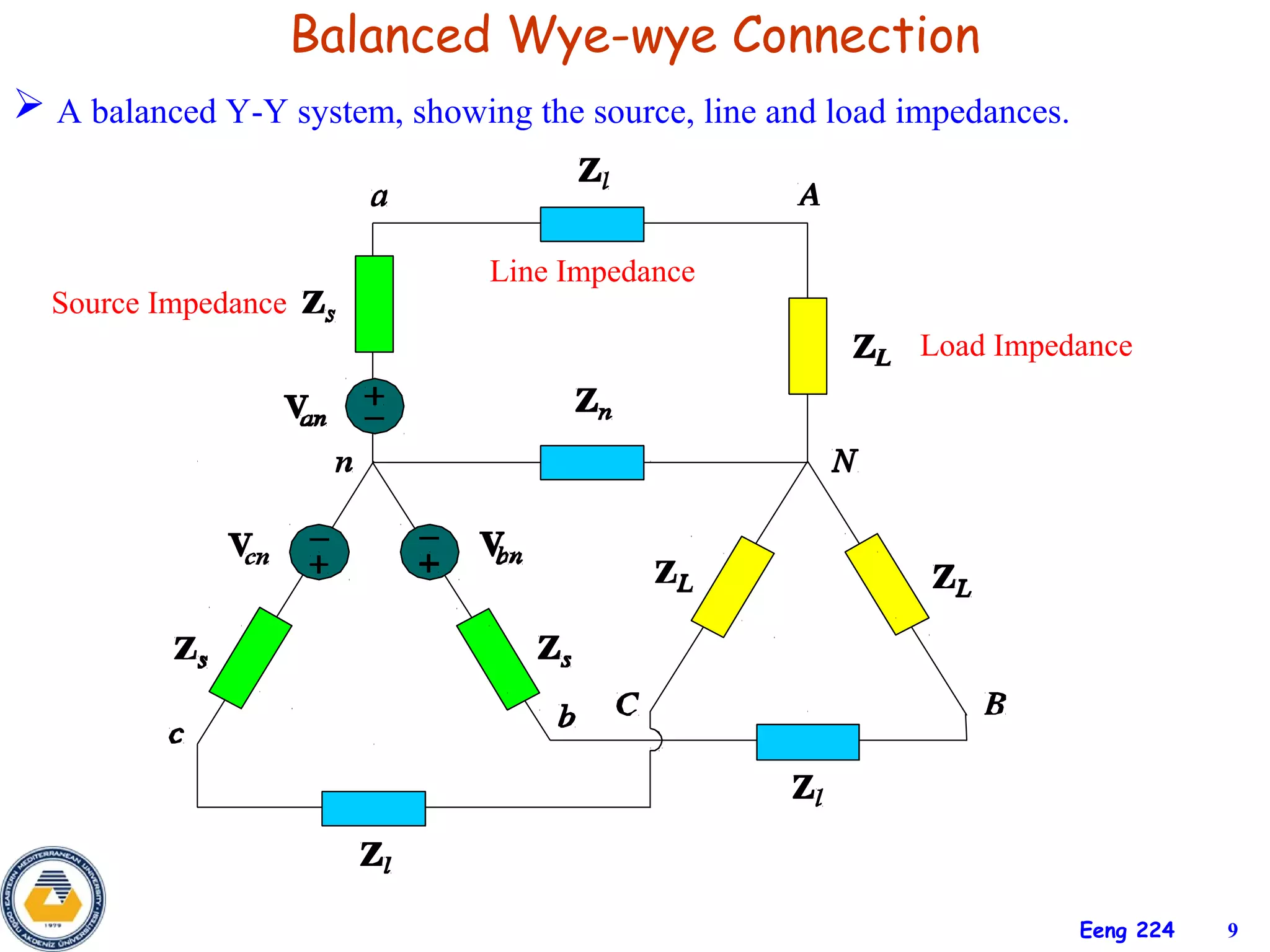
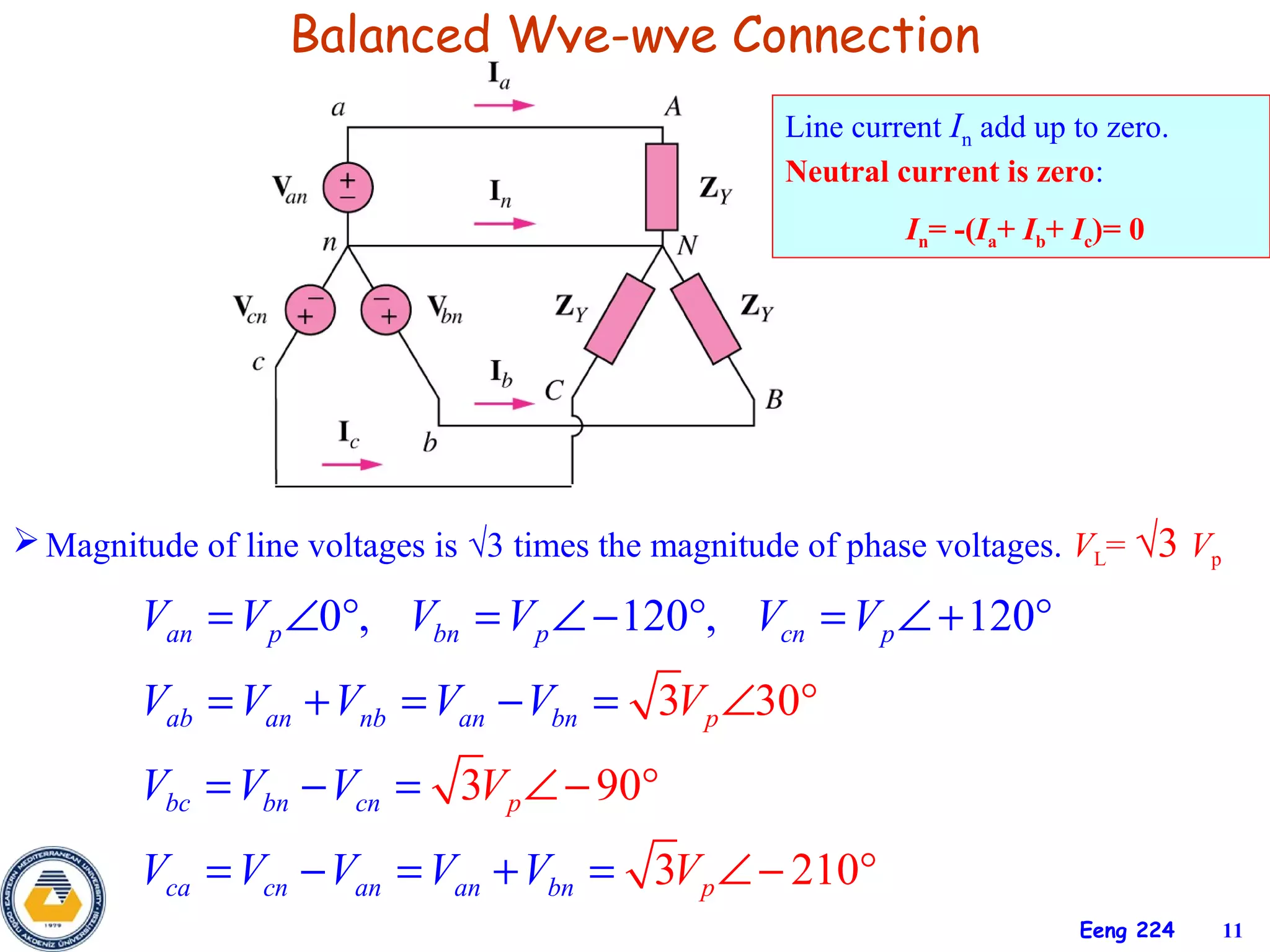
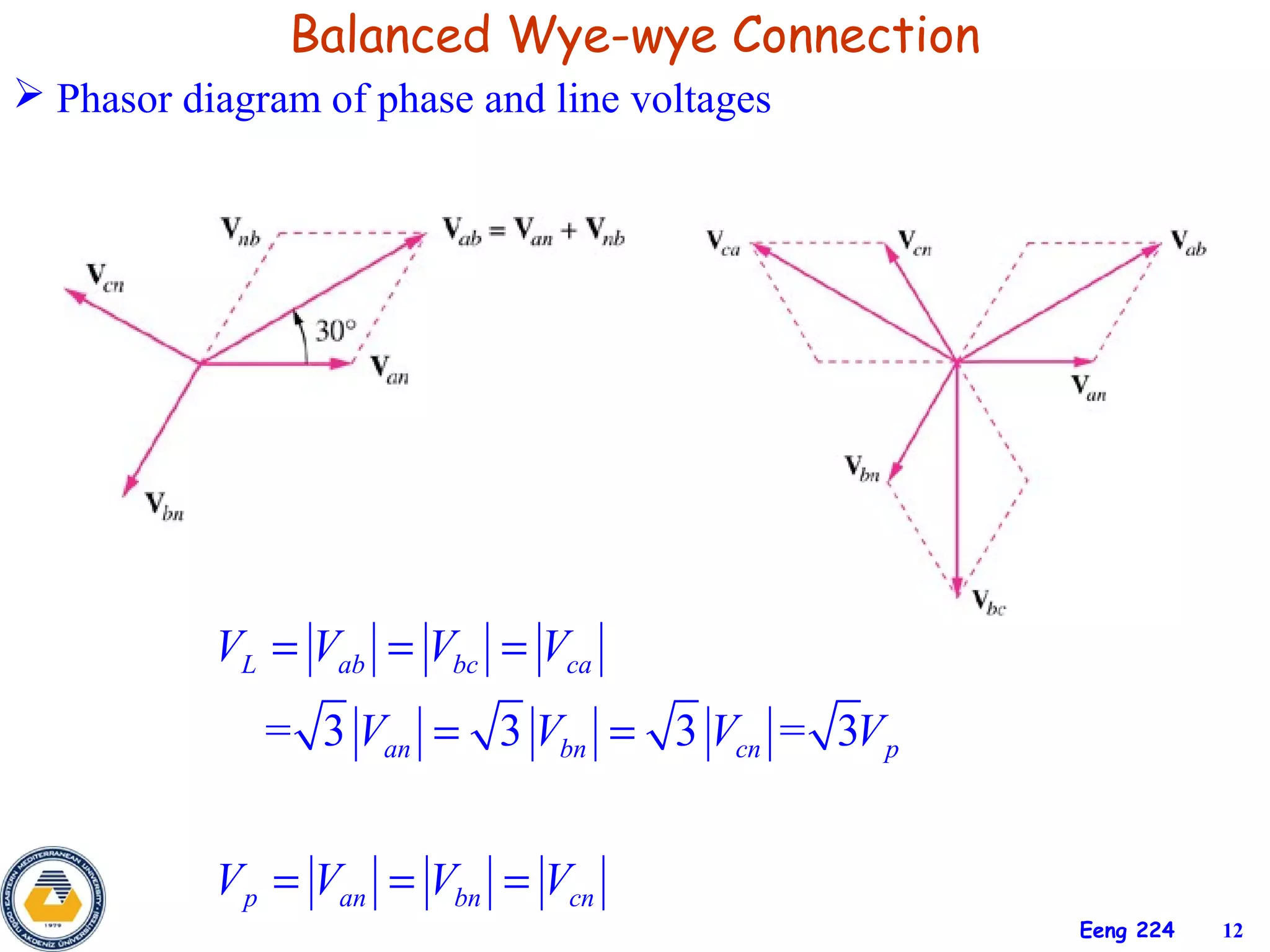
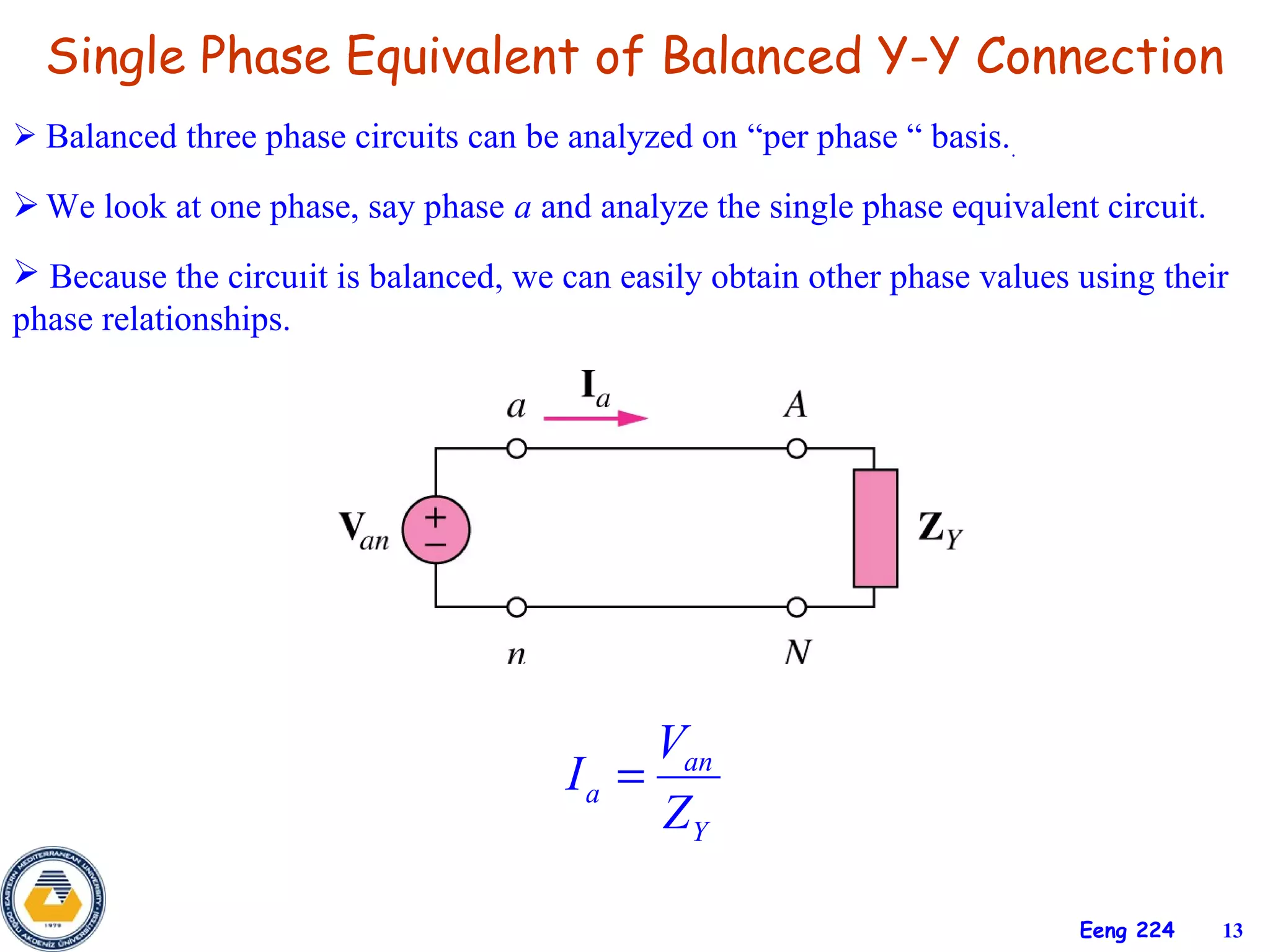
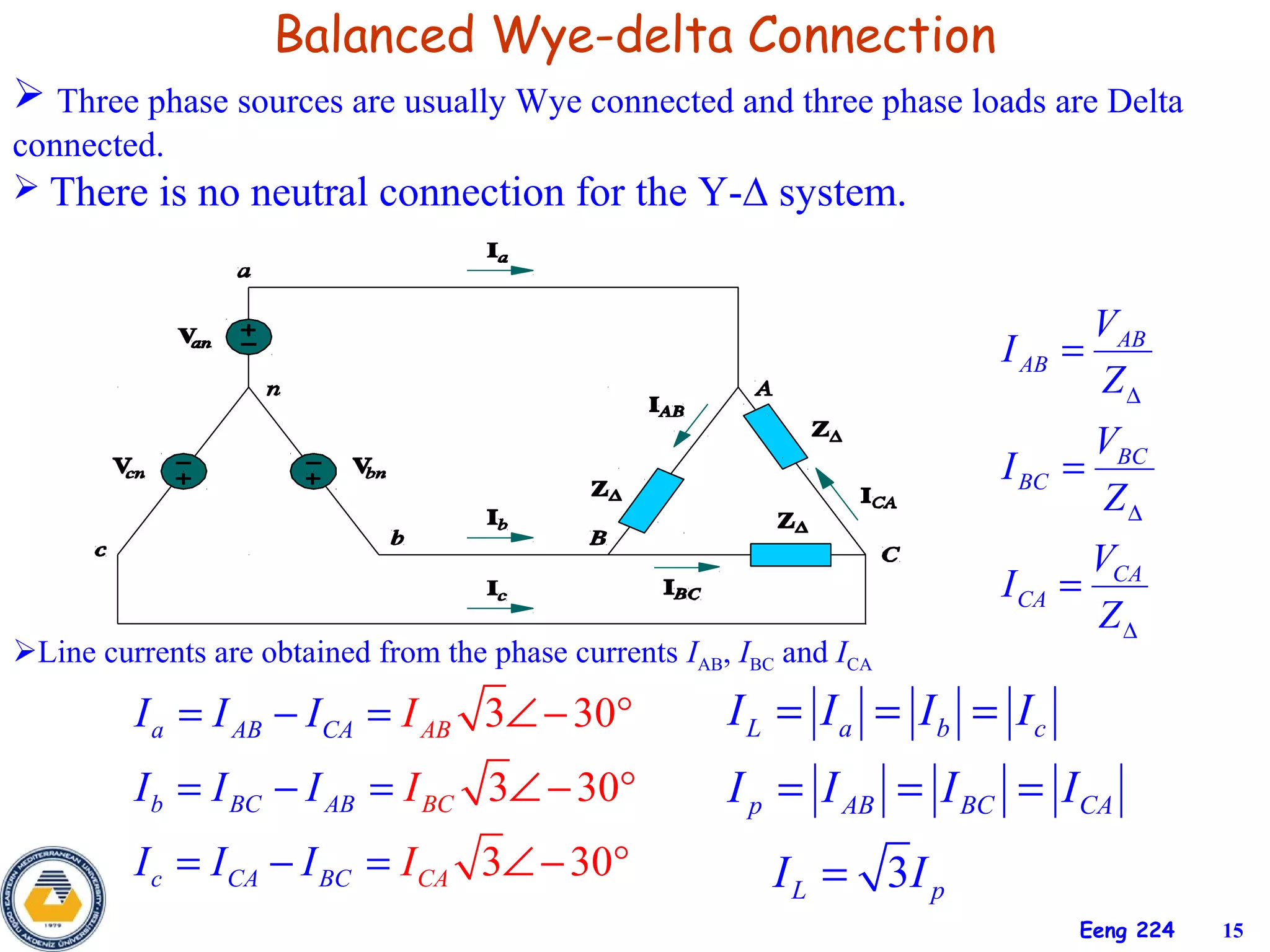
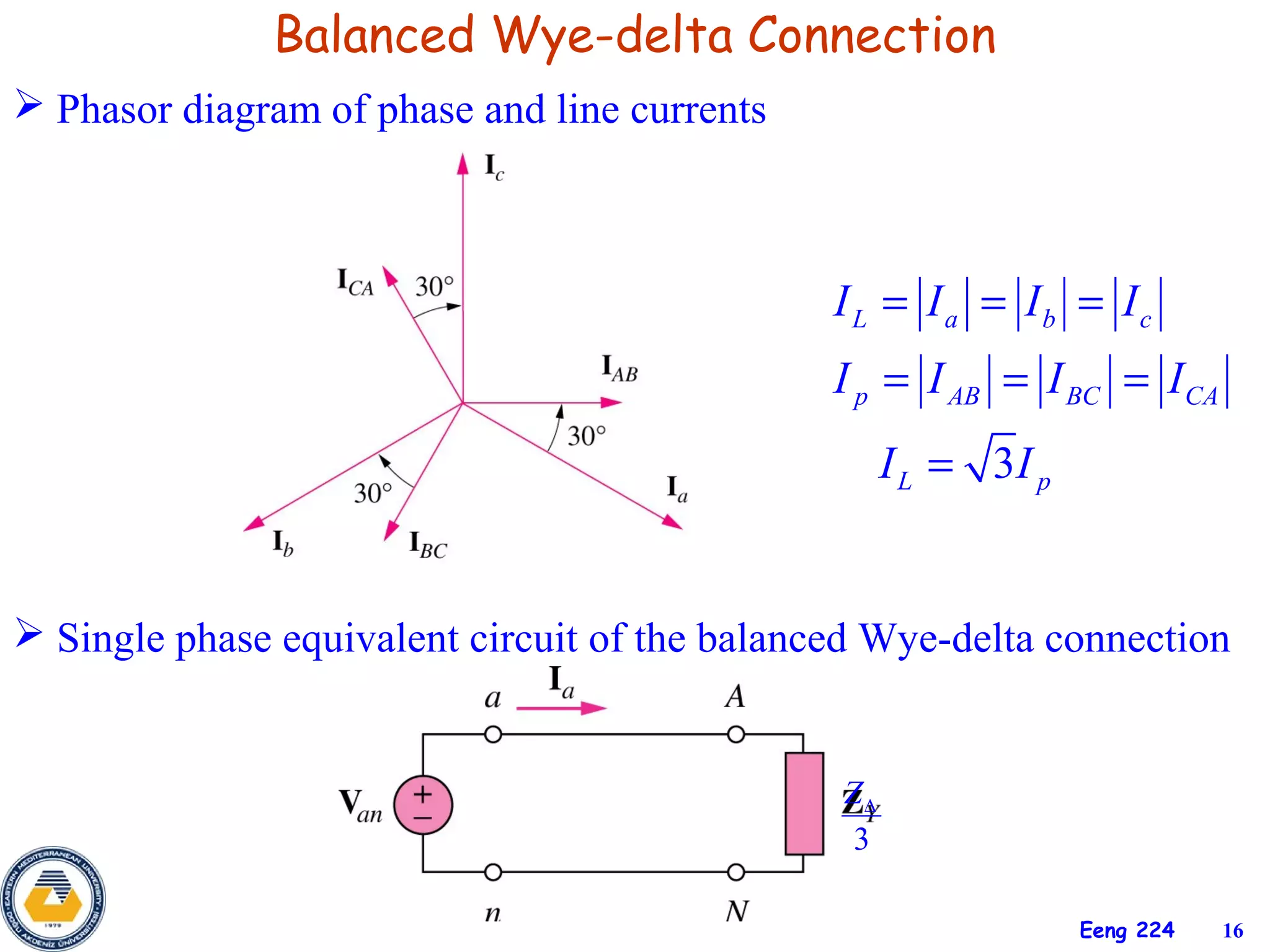
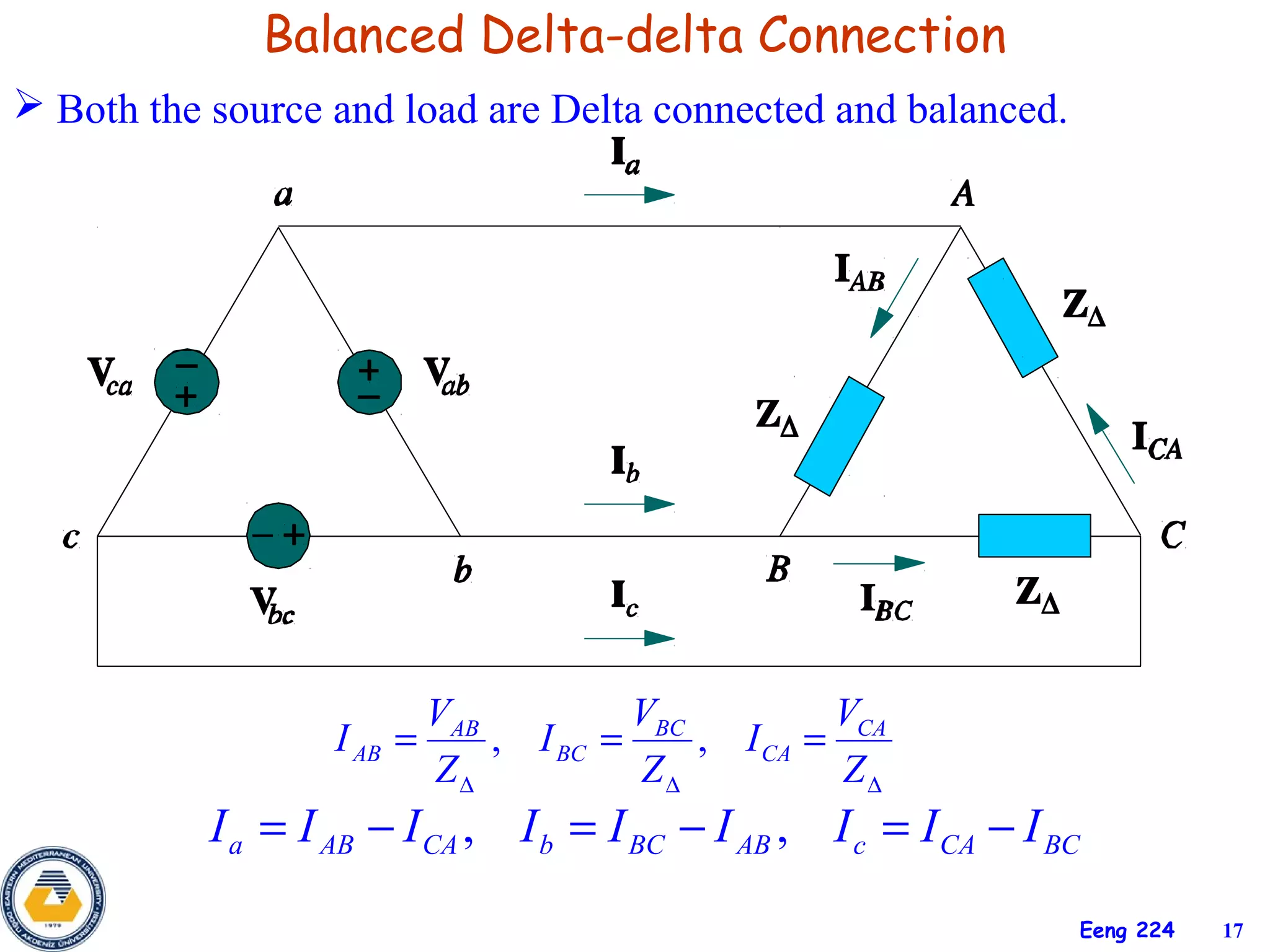
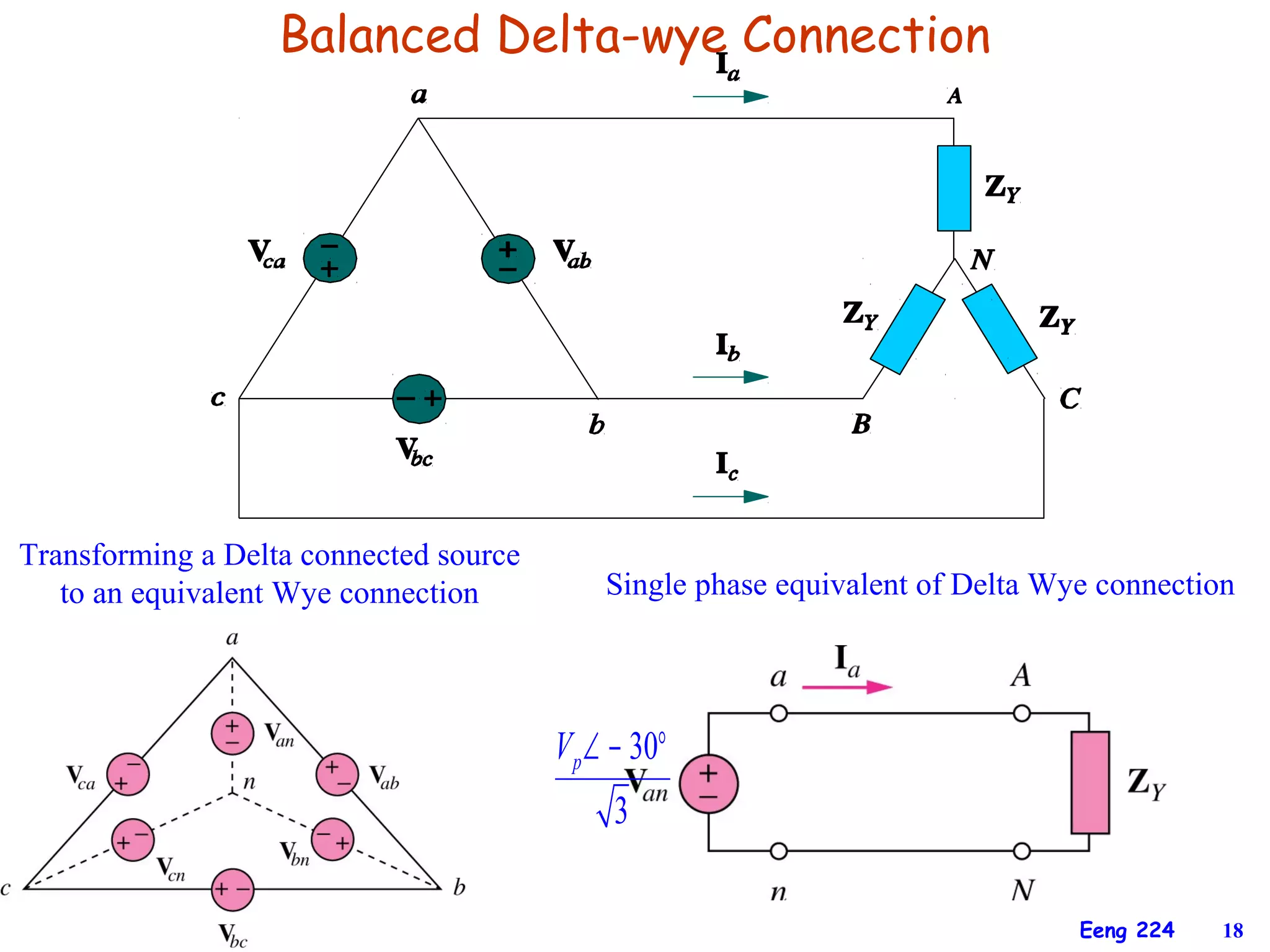
The document discusses three-phase circuits and their analysis. It covers balanced and unbalanced three-phase configurations, power in balanced systems, and analyzing unbalanced systems using PSpice. The objectives are to understand different three-phase connections, distinguish balanced and unbalanced circuits, calculate power in balanced systems, analyze unbalanced systems, and apply the concepts to measurement and residential wiring. Key points covered include wye-wye, wye-delta, delta-delta, and delta-wye connections for both sources and loads.

1. Chapter 12
Three Phase Circuits
Chapter Objectives:
 Be familiar with different three-phase configurations and how to
analyze them.
 Know the difference between balanced and unbalanced circuits
 Learn about power in a balanced three-phase system
 Know how to analyze unbalanced three-phase systems
 Be able to use PSpice to analyze three-phase circuits
 Apply what is learnt to three-phase measurement and residential
wiring
Huseyin Bilgekul
Eeng224 Circuit Theory II
Department of Electrical and Electronic Engineering
Eastern Mediterranean University Eeng 224 1

2. Three phase Circuits
 An AC generator designed to develop a single sinusoidal voltage for each rotation
of the shaft (rotor) is referred to as a single-phase AC generator.
 If the number of coils on the rotor is increased in a specified manner, the result is
a Polyphase AC generator, which develops more than one AC phase voltage per
rotation of the rotor
 In general, three-phase systems are preferred over single-phase systems for the
transmission of power for many reasons.
1. Thinner conductors can be used to transmit the same kVA at the same voltage,
which reduces the amount of copper required (typically about 25% less).
2. The lighter lines are easier to install, and the supporting structures can be less
massive and farther apart.
3. Three-phase equipment and motors have preferred running and starting
characteristics compared to single-phase systems because of a more even flow of
power to the transducer than can be delivered with a single-phase supply.
4. In general, most larger motors are three phase because they are essentially self-
starting and do not require a special design or additional starting circuitry.
Eeng 224 2

3. Single Phase, Three phase Circuits
b) Single phase systems three-wire type.
a) Single phase systems two-wire type Allows connection to both 120 V and
240 V.
Two-phase three-wire system. The AC sources
operate at different phases. Eeng 224 3

4. Three-phase Generator
 The three-phase generator has three induction coils placed 120° apart on the stator.
 The three coils have an equal number of turns, the voltage induced across each coil
will have the same peak value, shape and frequency.
Eeng 224 4

5. Balanced Three-phase Voltages
Three-phase four-wire system
Neutral Wire
A Three-phase Generator
Voltages having 120° phase difference
Eeng 224 5

6. Balanced Three phase Voltages
Neutral Wire
a) Wye Connected Source b) Delta Connected Source
Van = V p ∠0° Van = V p ∠0°
Vbn = V p ∠ − 120° Vbn = V p ∠ + 120°
Vcn = V p ∠ − 240° Vcn = V p ∠ + 240°
a) abc or positive sequence b) acb or negative sequence Eeng 224 6

7. Balanced Three phase Loads
 A Balanced load has equal impedances on all the phases
a) Wye-connected load b) Delta-connected load
Balanced Impedance Conversion:
Conversion of Delta circuit to Wye or Wye to Delta.
ZY = Z1 = Z 2 = Z 3
Z ∆ = Z a = Zb = Zc
1
Z ∆ = 3Z Y ZY = Z ∆
3
Eeng 224 7

8. Three phase Connections
 Both the three phase source and the three phase load can be
connected either Wye or DELTA.
 We have 4 possible connection types.
• Y-Y connection
• Y-Δ connection
• Δ-Δ connection
• Δ-Y connection
 Balanced Δ connected load is more common.
 Y connected sources are more common.
Eeng 224 8

9. Balanced Wye-wye Connection
 A balanced Y-Y system, showing the source, line and load impedances.
Line Impedance
Source Impedance
Load Impedance
Eeng 224 9

10. Balanced Wye-wye Connection
Line current In add up to zero.
Neutral current is zero:
In= -(Ia+ Ib+ Ic)= 0
 Phase voltages are: Van, Vbn and Vcn.
 The three conductors connected from a to A, b to B and c to C are called LINES.
 The voltage from one line to another is called a LINE voltage
 Line voltages are: Vab, Vbc and Vca
 Magnitude of line voltages is √3 times the magnitude of phase voltages. VL= √3 Vp
Eeng 224 10

11. Balanced Wye-wye Connection
Line current In add up to zero.
Neutral current is zero:
In= -(Ia+ Ib+ Ic)= 0
 Magnitude of line voltages is √3 times the magnitude of phase voltages. VL= √3 Vp
Van = V p ∠0°, Vbn = V p ∠ − 120°, Vcn = V p ∠ + 120°
Vab = Van + Vnb = Van − Vbn = 3V p ∠30°
Vbc = Vbn − Vcn = 3V p ∠ − 90°
Vca = Vcn − Van = Van + Vbn = 3V p ∠ − 210°
Eeng 224 11

12. Balanced Wye-wye Connection
 Phasor diagram of phase and line voltages
VL = Vab = Vbc = Vca
= 3 Van = 3 Vbn = 3 Vcn = 3V p
V p = Van = Vbn = Vcn
Eeng 224 12

13. Single Phase Equivalent of Balanced Y-Y Connection
 Balanced three phase circuits can be analyzed on “per phase “ basis..
 We look at one phase, say phase a and analyze the single phase equivalent circuit.
 Because the circuıit is balanced, we can easily obtain other phase values using their
phase relationships.
Van
Ia =
ZY
Eeng 224 13

14. Eeng 224 14

15. Balanced Wye-delta Connection
 Three phase sources are usually Wye connected and three phase loads are Delta
connected.
 There is no neutral connection for the Y-∆ system.
VAB
I AB =
Z∆
VBC
I BC =
Z∆
VCA
I CA =
Z∆
Line currents are obtained from the phase currents IAB, IBC and ICA
I a = I AB − I CA = I AB 3∠ − 30° I L = I a = Ib = Ic
I b = I BC − I AB = I BC 3∠ − 30° I p = I AB = I BC = I CA
I c = I CA − I BC = I CA 3∠ − 30° I L = 3I p
Eeng 224 15

16. Balanced Wye-delta Connection
 Phasor diagram of phase and line currents
I L = I a = Ib = Ic
I p = I AB = I BC = I CA
I L = 3I p
 Single phase equivalent circuit of the balanced Wye-delta connection
Z∆
3
Eeng 224 16

17. Balanced Delta-delta Connection
 Both the source and load are Delta connected and balanced.
VAB VBC VCA
I AB = , I BC = , I CA =
Z∆ Z∆ Z∆
I a = I AB − I CA , I b = I BC − I AB , I c = I CA − I BC
Eeng 224 17

18. Balanced Delta-wye Connection
Transforming a Delta connected source
to an equivalent Wye connection Single phase equivalent of Delta Wye connection
Vp ∠ − 30°
3
Eeng 224 18