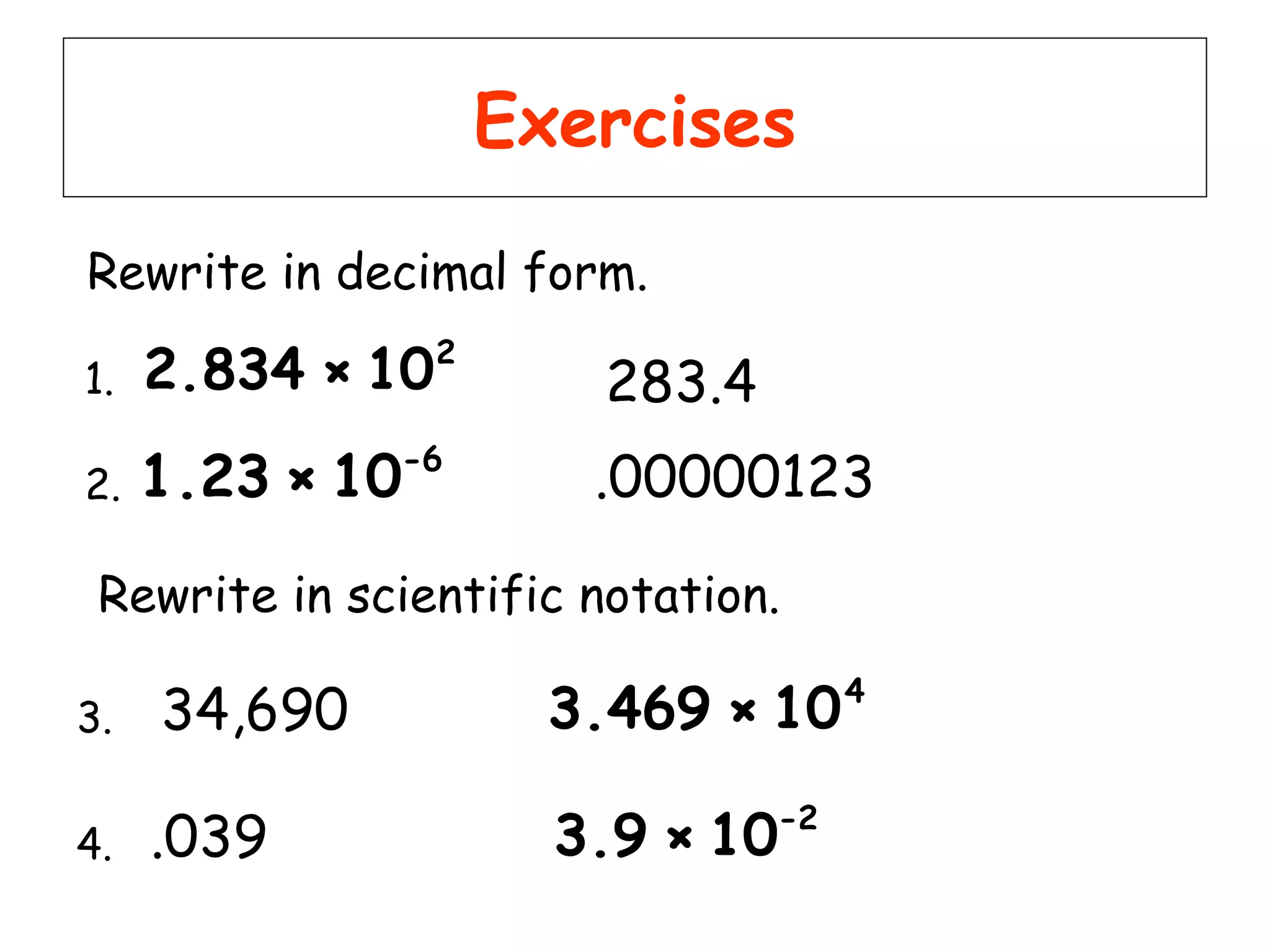
1) Scientific notation is a way of writing numbers in the form c × 10n, where c is between 1 and 10 and n is an integer.
2) Scientific notation allows very large and very small numbers to be written easily without lots of zeros by moving the decimal point and changing the exponent.
3) Operations like multiplication and division with scientific notation follow the normal rules of exponents - the exponents are added or subtracted.