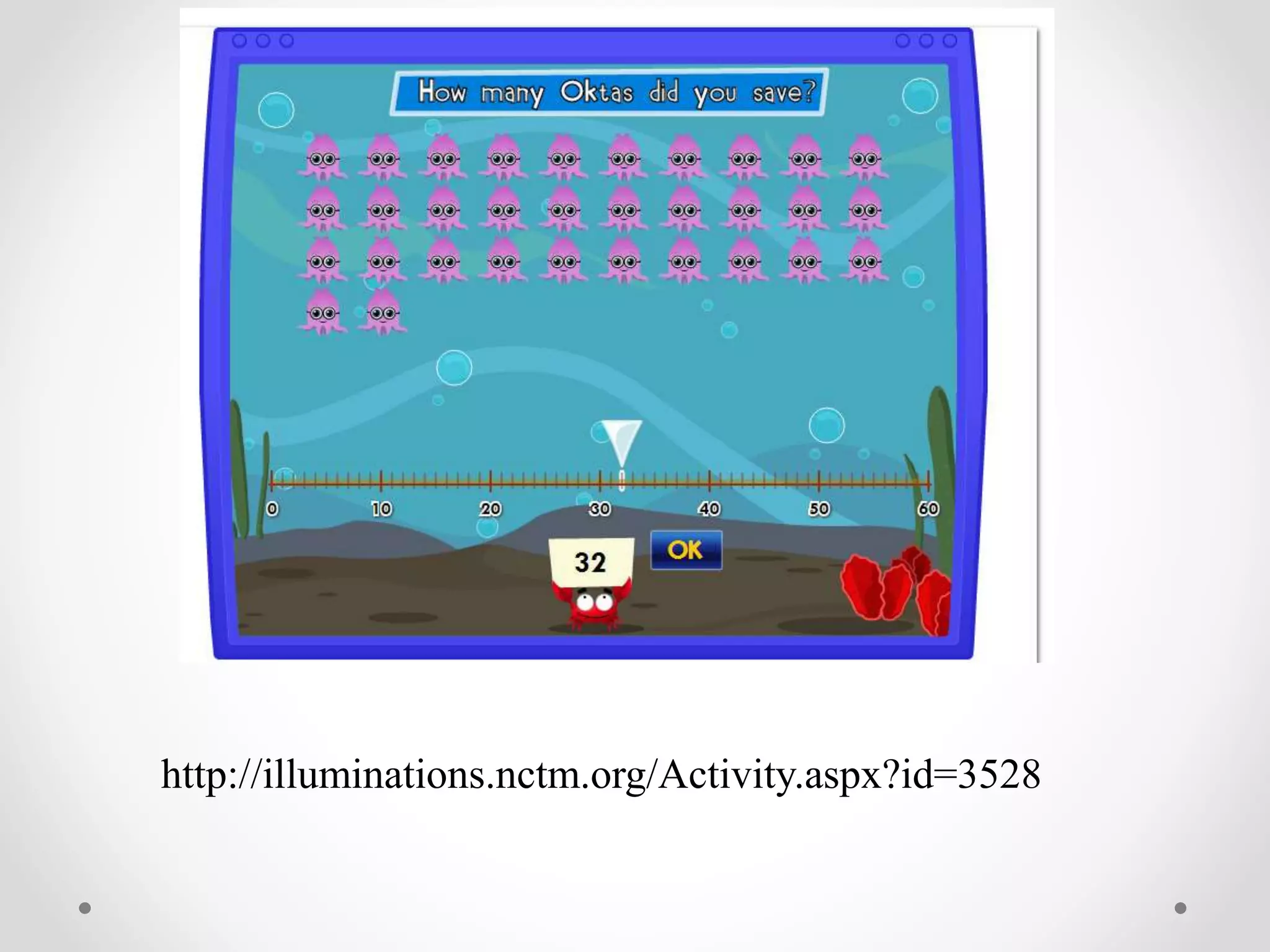
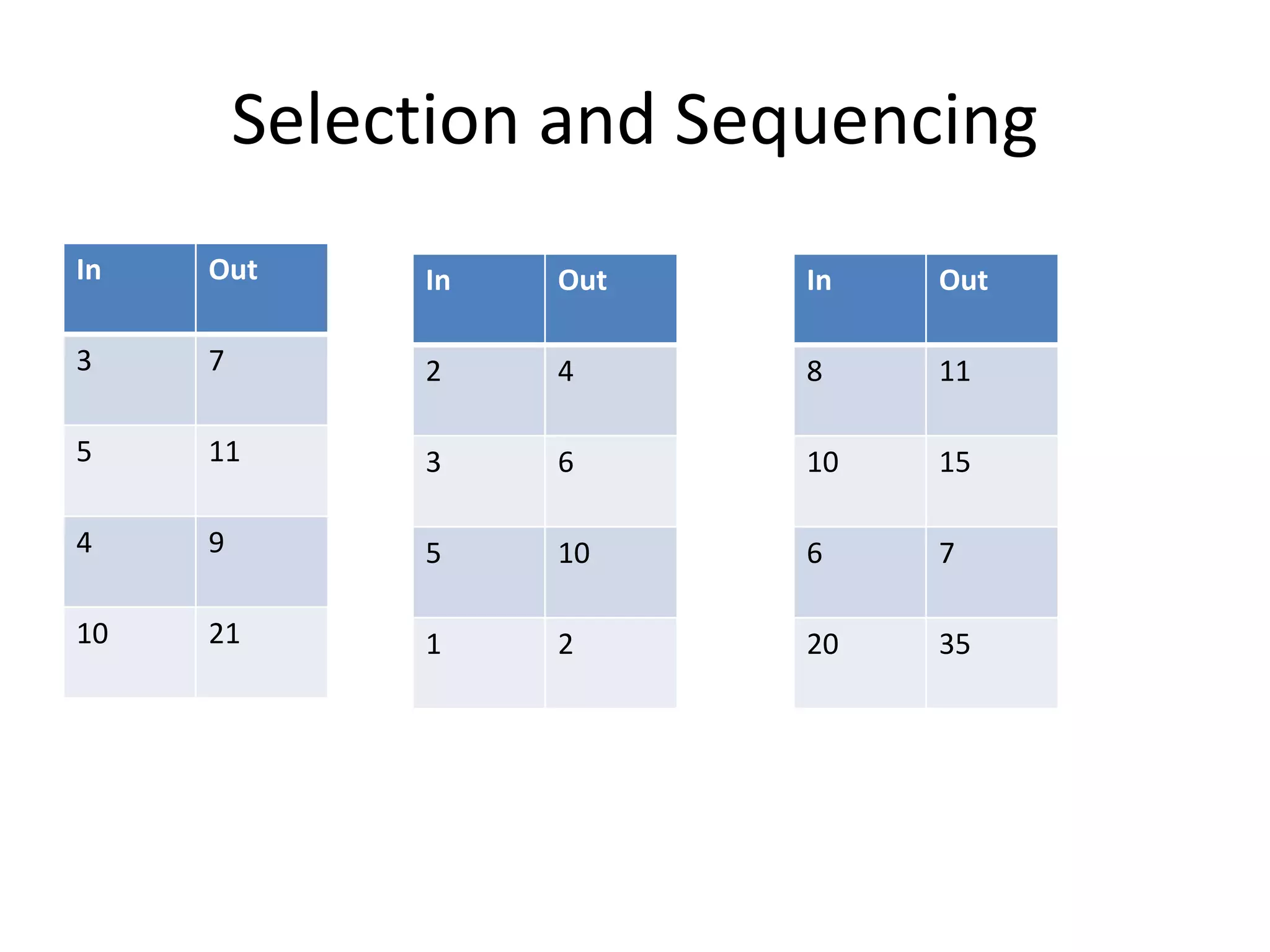
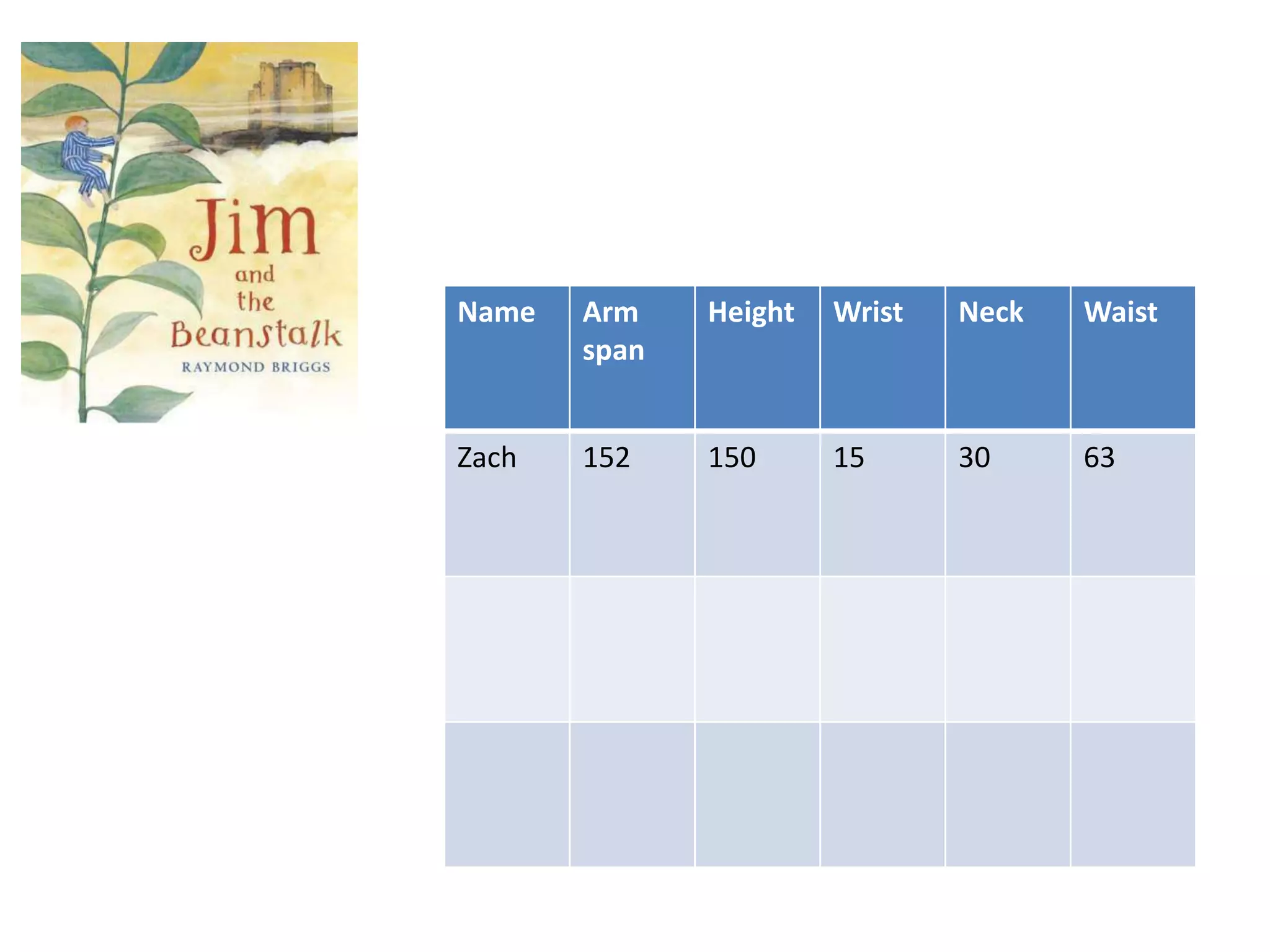
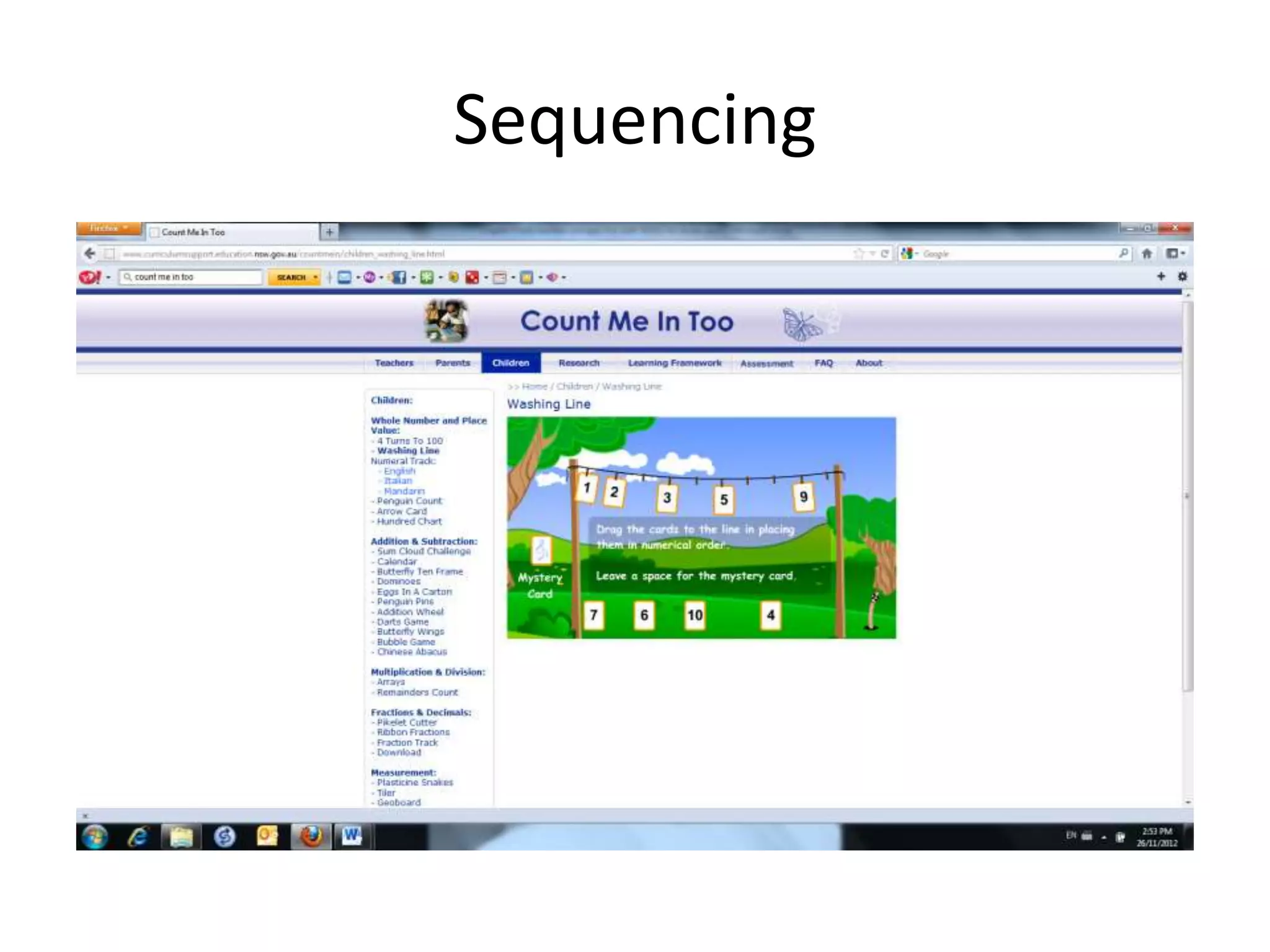
The document discusses effective mathematics teaching in early education, highlighting important characteristics and principles of numeracy instruction. It emphasizes the role of teacher knowledge, anticipating student responses, and creating authentic mathematical opportunities through structured tasks and discussion. The need for teachers to recognize and address students' misconceptions in mathematics is also stressed.

1. Creating Mathematical Opportunities in
the Early Years
Dr Tracey Muir
University of Tasmania
AAMT Connect with
Maths
26th August 2014

2. Background
Launceston

3. Overview
• What does effective mathematics teaching
look like?
• What types of knowledge does an effective
teacher require?
• How can we provide students with
authentic mathematical opportunities?
• What aspects of classroom practice should
we focus on in order to maximise
mathematical opportunities?

4. Connectionist, transmission and
discovery beliefs
Connectionist Transmission Discovery
The use of methods of
Primarily the ability to
calculation which are
perform standard
both efficient and
procedures or routines
effective
Finding the answer to a
calculation by any
method
Confidence and ability in
mental methods
A heavy reliance on
paper and pencil
methods
A heavy reliance on
practical methods
Pupil misunderstandings
need to be recognised,
made explicit and worked
on
Pupils’
misunderstandings are
the result of ‘grasp’ what
was being taught and
need to be remedied by
further reinforcement of
the ‘correct’ method
Pupils’
misunderstandings are
the results of pupils not
being ready to learn the
ideas
(Askew, et al., 1997)

5. Characteristics of effective
numeracy teachers
•Emphasise the importance of understanding mathematical
concepts and the connections between these
•Have high expectations that all children will engage seriously
with mathematical ideas
•Structure purposeful tasks that enable different possibilities,
strategies and products to emerge
•Probe and challenge children’s thinking and reasoning
•Build on children’s mathematical ideas and strategies
•Are confident in their own knowledge of mathematics at the
level they are teaching
(Groves et al., 2006)

6. Principles of practice
•Make connections
•Challenge all pupils
•Teach for conceptual understanding
•Purposeful discussion
•Focus on mathematics
•Convey and instill positive attitudes
towards mathematics

7. Teaching actions
• Choice of examples
• Choice of tasks
• Questioning
• Use of representations
• Modelling
• Teachable moments

9. How familiar is term PCK?
(Vote)

10. • Teacher knowledge
(Ball, Thames, & Phelps, 2008)

11. 5 Practices
• Anticipating
• Monitoring
• Selecting
• Sequencing
• Connecting
(Smith & Stein, 2011)

12. Anticipating
• Planning for ‘teachable moments’
• Knowing your subject and the difficulties
students might encounter
• Experience, research and reflection
• Highlighting possible misconceptions in
planning

13. Pre-planning
• What do I need to know and understand
before teaching this topic?
• What are the likely difficulties or
misconceptions students may have?

14. Measurement opportunities

15. Devise task
• What are some activities or tasks you could
undertake to explore ‘Mr Splash’?

16. • This is a photograph of Mr. Splash. He loves to
have a bath in his pajamas. He seems to be a
bit big for the bath! I wonder how tall he is?
How could we find out?

17. • Does the tallest person have the longest feet?
• Does the tallest person have the greatest hand span?
• Are hand spans and foot lengths related?
• Are boys taller than girls?
• Draw a representation of Mr. Splash on the butcher paper.
• Estimate the following and explain your estimates:
– Mr. Splash’s height
– Mr. Splash’s height compared to the tallest person in class
– Mr. Splash’s height compared to the tallest person in your
family
– Mr. Splash’s height compared to the tallest person in the
world
• Explain whether you think Mr. Splash has the dimensions of a
real person.

18. What teacher knowledge is required?
• Content knowledge
• Curriculum knowledge
• PCK

19. Anticipating student responses
Measurement considerations:
• Selection of appropriate unit
• Measuring accurately with units (e.g., lining
up with no gaps, using the one unit)
• Confusion with formal units and conversions
(for older students)

20. In your groups, measure your
heights, arm spans, hand spans and
foot size (record these measures in
the following table).

21. Name Arm
span
Height Wrist Neck Waist
Zach 152 150 15 30 63

23. More informal
measurement
• Story
• Book
• Clip
• Interactive website
• Scenario
• http://www.mwpenn.com/lesson-plans/lesson-plan-for-
how-big-is-a-foot/
• http://illuminations.nctm.org/LessonDetail.aspx?ID=L
205

25. What do I need to know/consider about
topic?

26. What do I need to know/consider about
topic?
• Length refers to the measurement of something from end to end
• Sequence for teaching measurement
• Children need to experience the usefulness of non-standard units
• There are a number of principles to consider when asking
students to measure with non-standard units:
• The unit must not change – for example, we should select one
type of informal unit, such as straws, to measure the length of the
table, rather than a straw, pencil and rubber
• The units must be placed end to end (when measuring length),
with no gaps or overlapping units
• The unit needs to be used in a uniform manner – i.e., if dominoes
are being used to find the area of the top of a desk, then each
domino needs to be placed in the same orientation in order to
accurately represent the standard unit
• There is a direct relationship between the size of the unit and the
number required – i.e., the smaller the unit, the bigger the number
and vice versa

27. What do I need to know about students’
learning of topic?
• Possible misconceptions
• Physical difficulties with measuring (e.g., physically
lining up units, etc)
• Individual considerations – how to differentiate the
task

28. Estimating – a teachable moment

29. Counting and early number
• Capitalise on ICT
https://www.youtube.com/w
atch?v=aXV-yaFmQNk
https://www.youtube.com/watc
h?v=MGMsT4qNA-c

30. Songs and Rhymes

31. Sequencing

32. Consider:
• What would be the advantages and
disadvantages of doing this activity online as
compared with using real materials in the
classroom?

33. Capitalising on the ICT

34. Bridging 10

35. • Teacher: Great. OK. This is what we do when we
bridge ten. We make one of the ten frames up into
ten by moving the dots [shows two ten frames on the
board next to each other, one with eight and one
with seven counters or dots] Which would be the
sensible one to move the dots in up here?
• Student: Move from the yellow one to the purple one
[ten frame]
• Teacher: Would you do that Jim? Would you fill up
the ten frame, the purple ten frame, with eight in it?
Would you be able to put the dots on the other side?
• [Jim moves the dots to the ten frame, and leaves a
column of three dots and a column of two dots in the
yellow frame]

36. • Teacher: Now can you arrange the other frame
so that all the dots are in a straight line?
• [Jim moves the dots so that they form a
column of 5]
• Teacher: Great, so what have we got?
• Jim: Five and ten
• Teacher: Which make?
• Jim: Fifteen

38. TPACK
Reproduced by permission
of the publisher, © 2012 by
tpack.org

39. Subitising – making it purposeful

40. Press Here
• https://www.youtube.com/watch?v=Kj81KC-Gm64

41. Thumbs up or down?
Google Images

42. http://illuminations.nctm.org/Activity.aspx?id=3528

43. Two of Everything
Google Images

44. Monitoring
• Paying close attention to students’
mathematical thinking and solution strategies
as they work on task
• Can assist through creating a list of possible
solutions before lesson (anticipating)
• Questioning – more than observing

45. Selection and Sequencing
In Out
3 7
5 11
4 9
10 21
In Out
2 4
3 6
5 10
1 2
In Out
8 11
10 15
6 7
20 35

46. Connecting
• Drawing connections between students’
solutions and the key mathematical ideas
• Goal is to have student presentations build on
one another to develop powerful
mathematical ideas

47. More than ‘sharing’
Who did it a
different way?

48. Factors influencing the planning and
uptake of mathematical
opportunities
• Teacher knowledge Content
knowledge, Pedagogical Content Knowledge (PCK)
(Shulman, 1987)
• Teacher beliefs What it is to be numerate
pupil, how pupils learn to become numerate, and
how best to teach pupils to become numerate

49. Choosing tasks to elicit
mathematical opportunities
• Connect naturally with what has been taught
• Addresses a range of outcomes in the one task
• Are time efficient and manageable
• Allow all students to make a ‘start’
• Engage the learner
• Provide a measure of choice or openness
• Encourage students to disclose their own
understanding of what they have learned
• Are themselves worthwhile activities for students’
learning (Downton, et al., 2006, p. 9)
13/10/2014

51. Place a number where you think it
would fit…

52. Counting on Frank
“I don’t mind having a bath – it
gives me time to think. For
example, I calculate it would take
eleven hours and forty-five minutes
to fill the entire bathroom with
water. That’s with both taps
running. It would take less time to
empty, as long as no one opened
the door!”
(Clements, 1990, unpaged)

53. Is it accurate?
“Going shopping with mum is a big event. She is
lucky to have such an intelligent trolley-pusher.
It takes forty-seven cans of dog food to
fill one trolley, but only one to knock over one
hundred and ten!”

54. • Does it really take 47 cans of dog food to fill
one trolley? Even allowing for different sized
trolleys and cans of dog food, this seems a
gross under-estimation. In order to test this
claim, a 12 year-old student, using real cans of
dog food (680 gram; 23.94 ounce tins) found
that it took approximately 47 cans of dog food
just to fill the base of a shopping trolley, and
that it would take closer to 216 cans to fill your
average shopping trolley.

55. Anticipating mathematical
opportunities
• Confusion between length, area and volume
(and capacity)
• Conversion of units
• Multiplication
• Dimensions of tins
• Consistency for comparison

56. Self reflection/feedback
Something that helped me learn …
Something I wasn’t sure about …
Something that stopped my learning

57. A couple of other favourites….
Google images

58. The wolf’s chicken stew

59. Useful resources

61. Conclusions
• Useful to consider the types of knowledge
required by teachers
• Mathematical opportunities can be
anticipated
• 5 practices are useful for orchestrating
productive mathematical discussions
• Mathematical opportunities are
everywhere – be creative but make them
purposeful

62. Useful references
Arafeh, S., Smerdon, B., & Snow, S. (2001, April 10-15). Learning from teachable moments: Methodological
lessons from the secondary analysis of the TIMSS video study. Paper presented at the Annual Meeting of the
American Educational Research Association, Seattle, WA.
Askew, M. (2005). It ain't (just) what you do: effective teachers of numeracy. In I. Thompson (Ed.), Issues in
teaching numeracy in primary schools (pp. 91-102). Berkshire, UK: Open University Press.
Askew, M., Brown, M., Rhodes, V., Johnson, D., & Wiliam, D. (1997). Effective teachers of numeracy. London:
School of Education, King's College.
Clarke, D., & Clarke, B. (2002). Challenging and effective teaching in junior primary mathematics: What does it
look like? In M. Goos & T. Spencer (Eds.), Mathematics making waves (Proceedings of the 19th Biennial
Conference of the Australian Association of Mathematics Teachers, pp. 309-318). Adelaide, SA: AAMT.
Groves, S., Mousley, J., & Forgasz, H. (2006). Primary Numeracy: A mapping, review and analysis of Australian
research in numeracy learning at the primary school level. Canberra, ACT: Commonwealth of Australia.
Muir, T. (2008). “Zero is not a number”: Teachable moments and their role in effective teaching of numeray. In
M. Goos, R. Brown & K. Makar (Eds.), Navigating currents and charting directions (Proceedings of the 31st
annual conference of the Mathematics Education Research Group of Australasia, Brisbane, pp. 361-367).
Adelaide, SA: MERGA.
Muir, T. (2008b, July 6-13). Describing effective teaching of numeracy: Links between principles of practice and
teacher actions. Paper presented at the 11th International Conference on Mathematics Education (ICME-11) for
Topic Study Group 2: New developments and trends in mathematics education at primary level, Monterrey,
Mexico.
Rowland, T., Turner, F., Thwaites, A., & Huckstep, P. (2009). Developing primary mathematics teaching: Reflecting
on practice with the knowledge quartet. London: SAGE Publications Ltd.
Smith, M. S., & Stein, M. K. (2011). 5 practices for orchestrating productive mathematical discussions. Reston,
VA: NCTM.