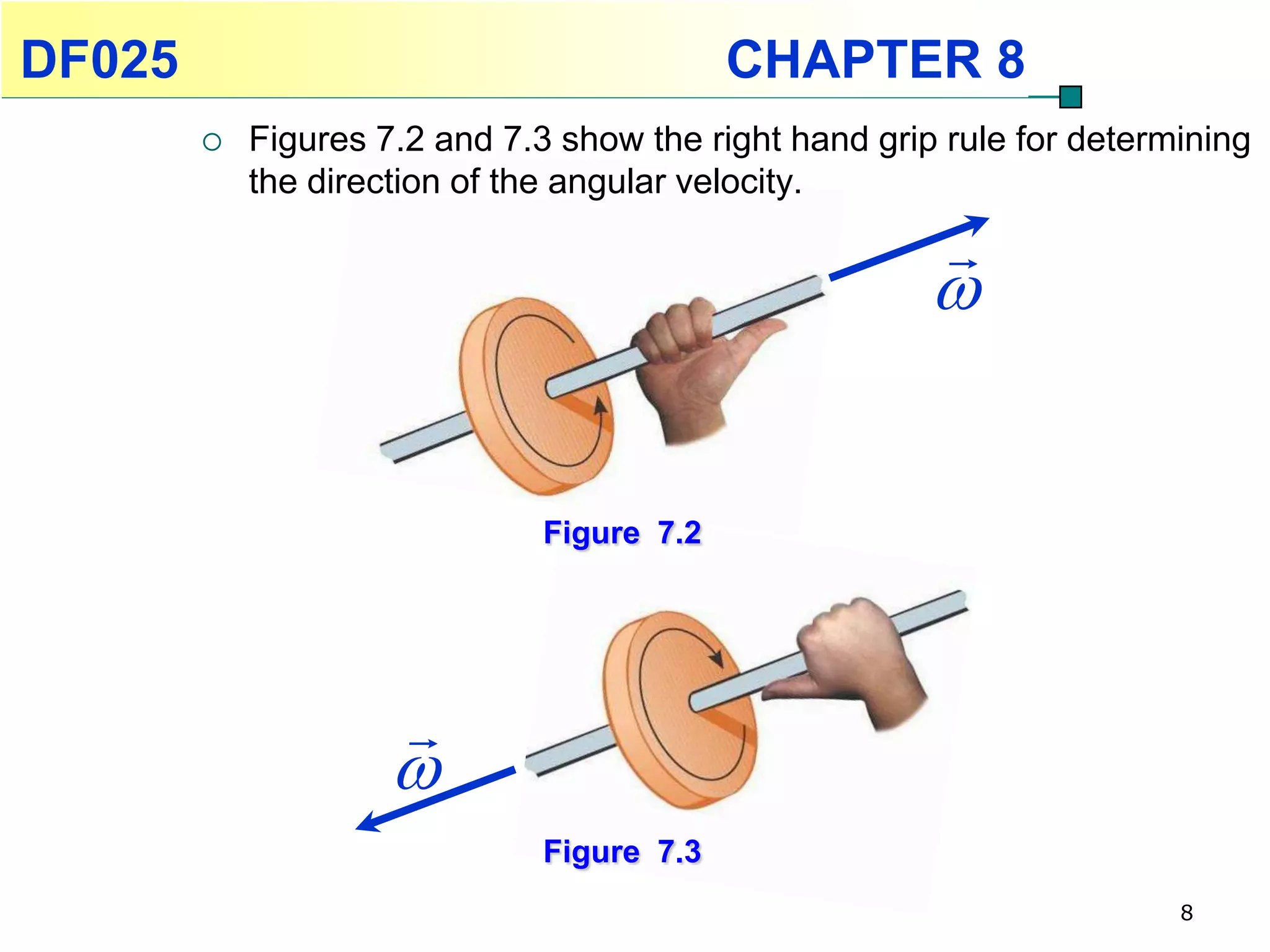
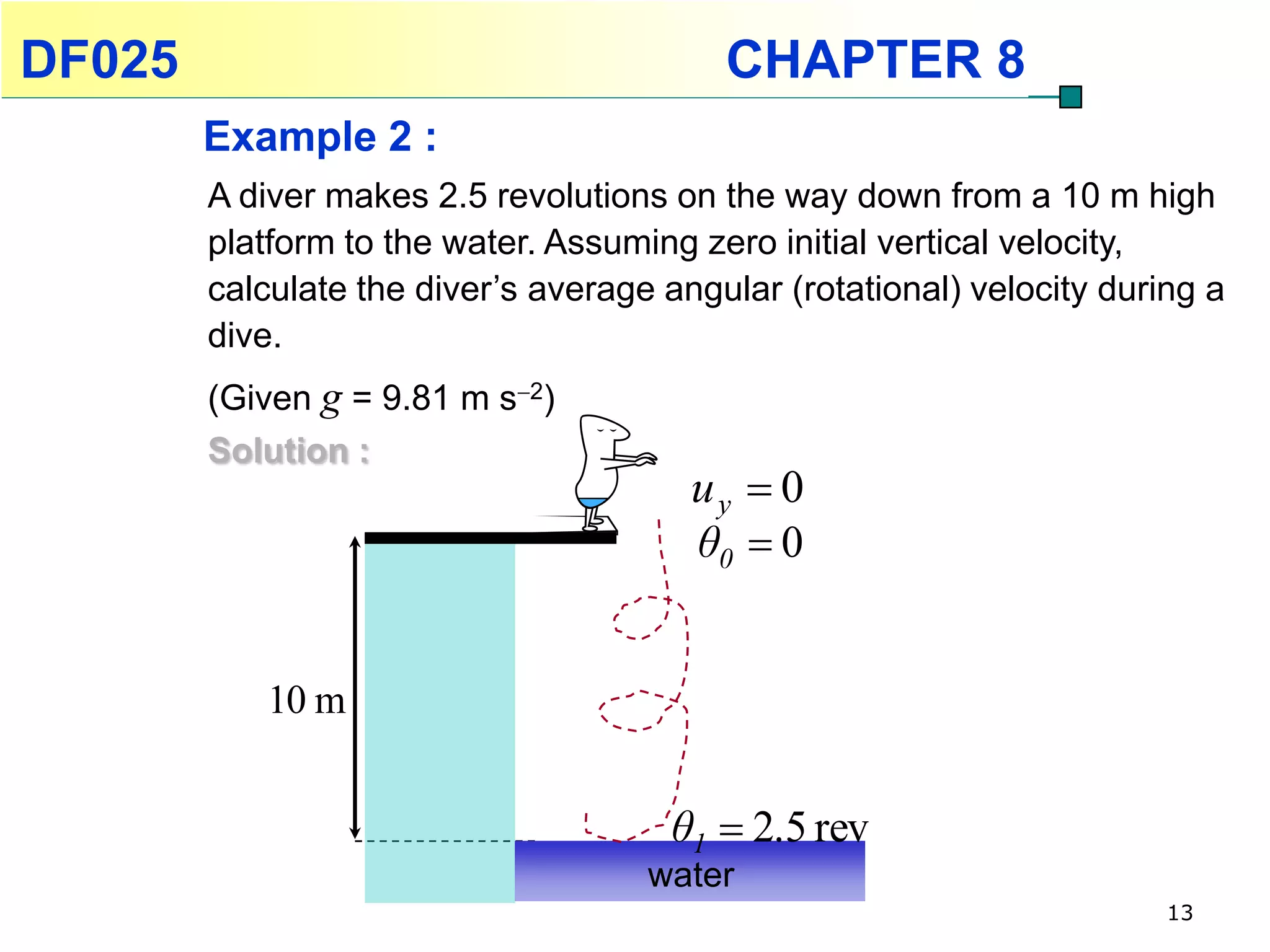
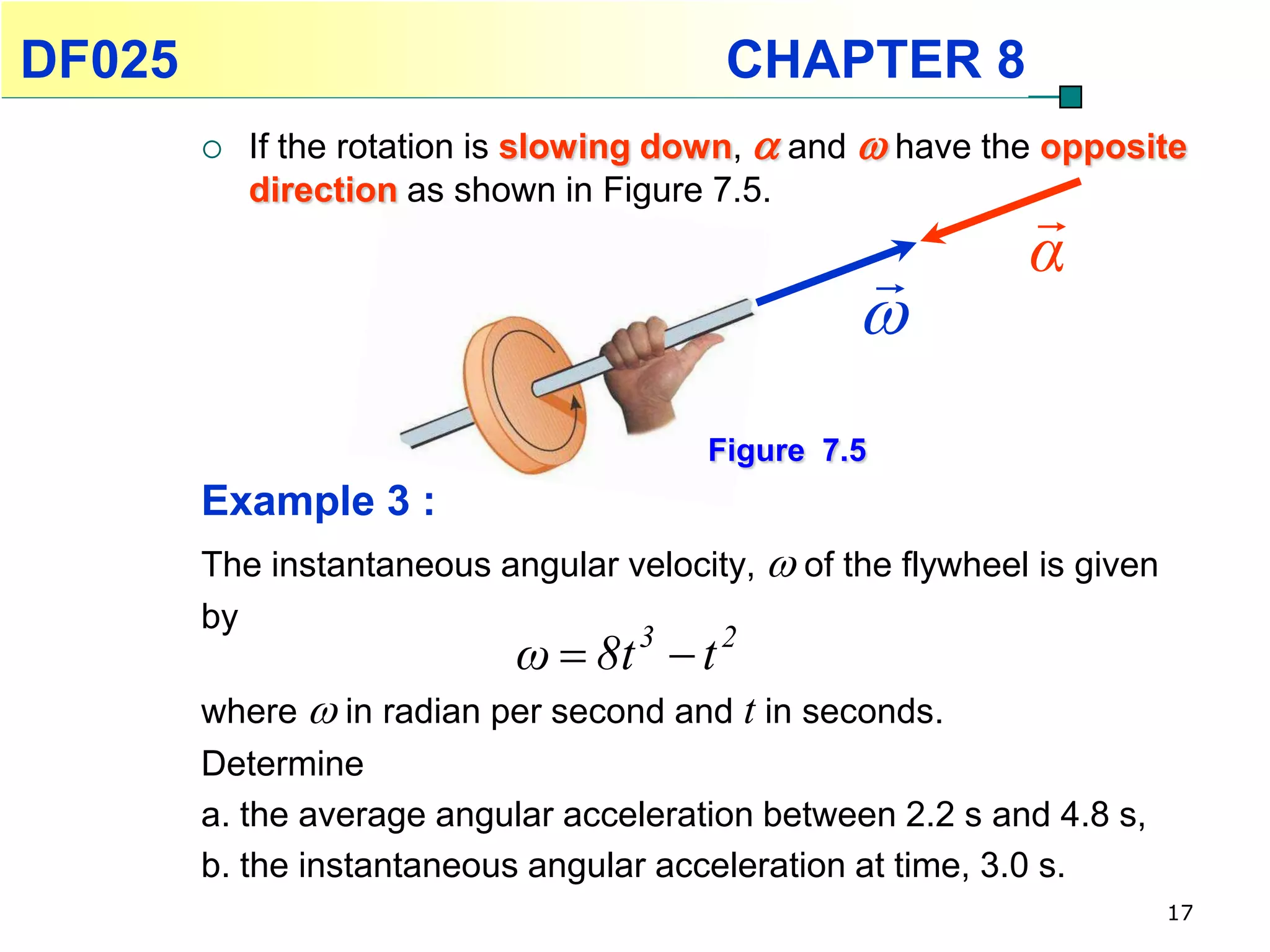
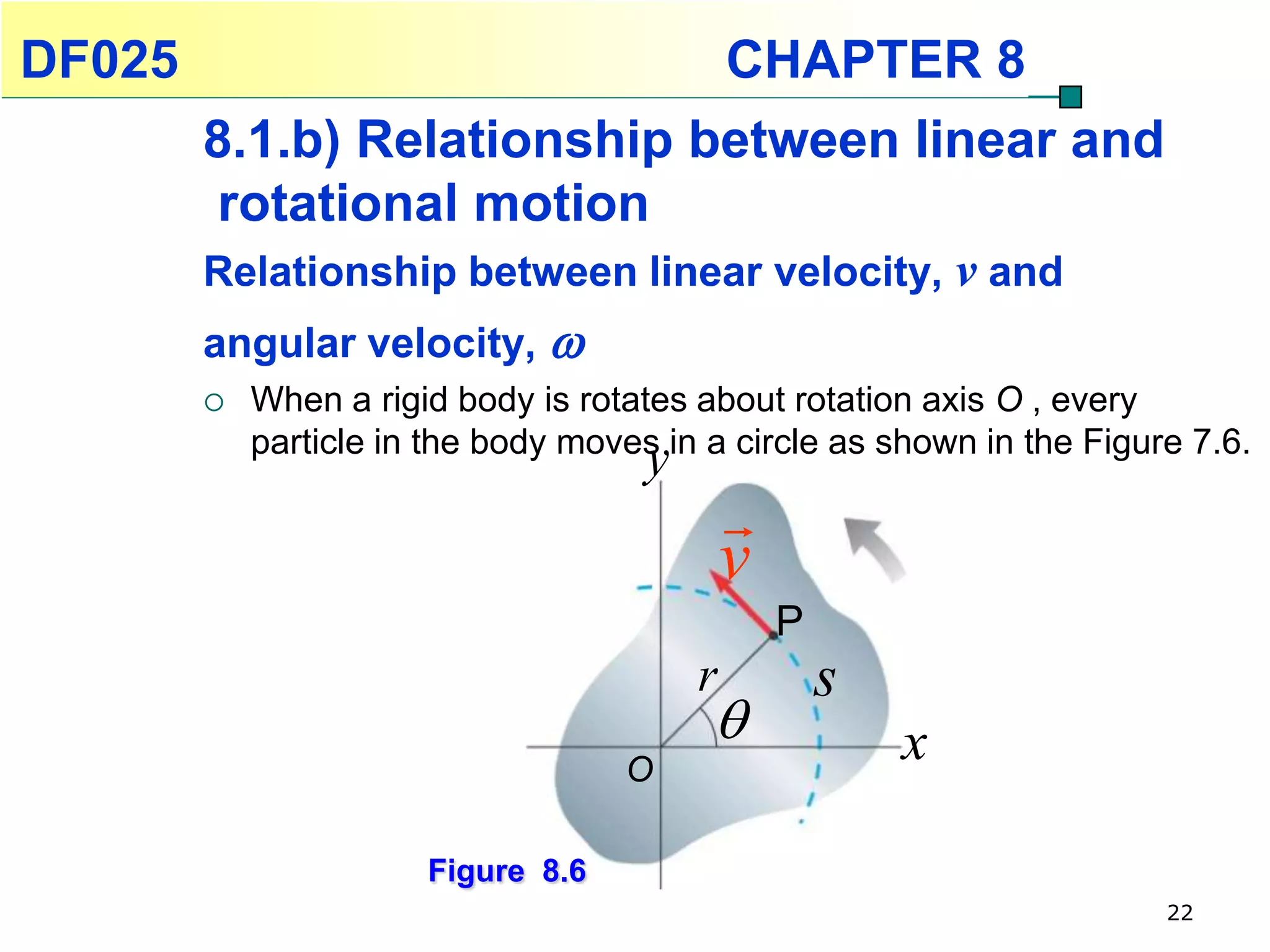
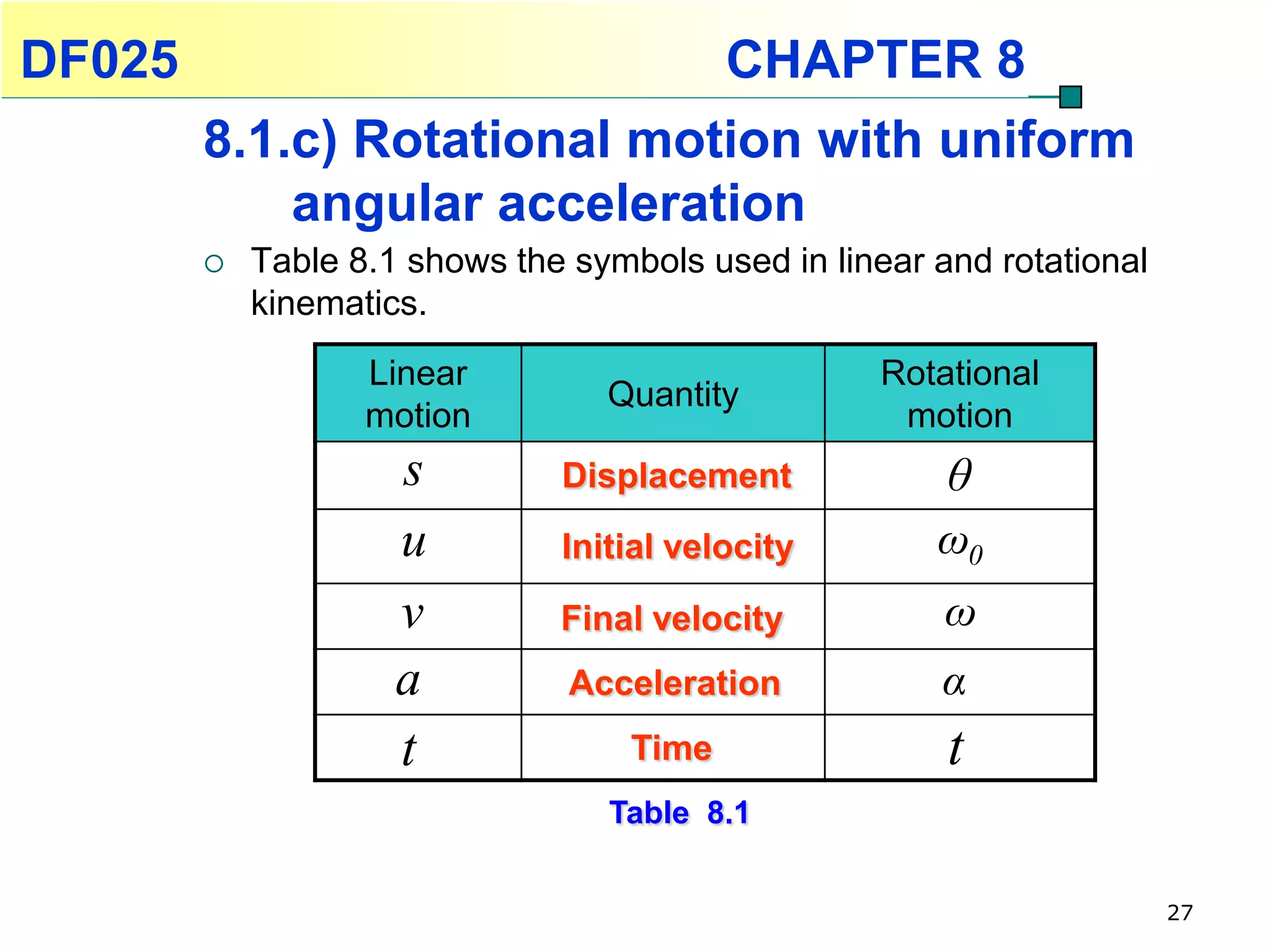
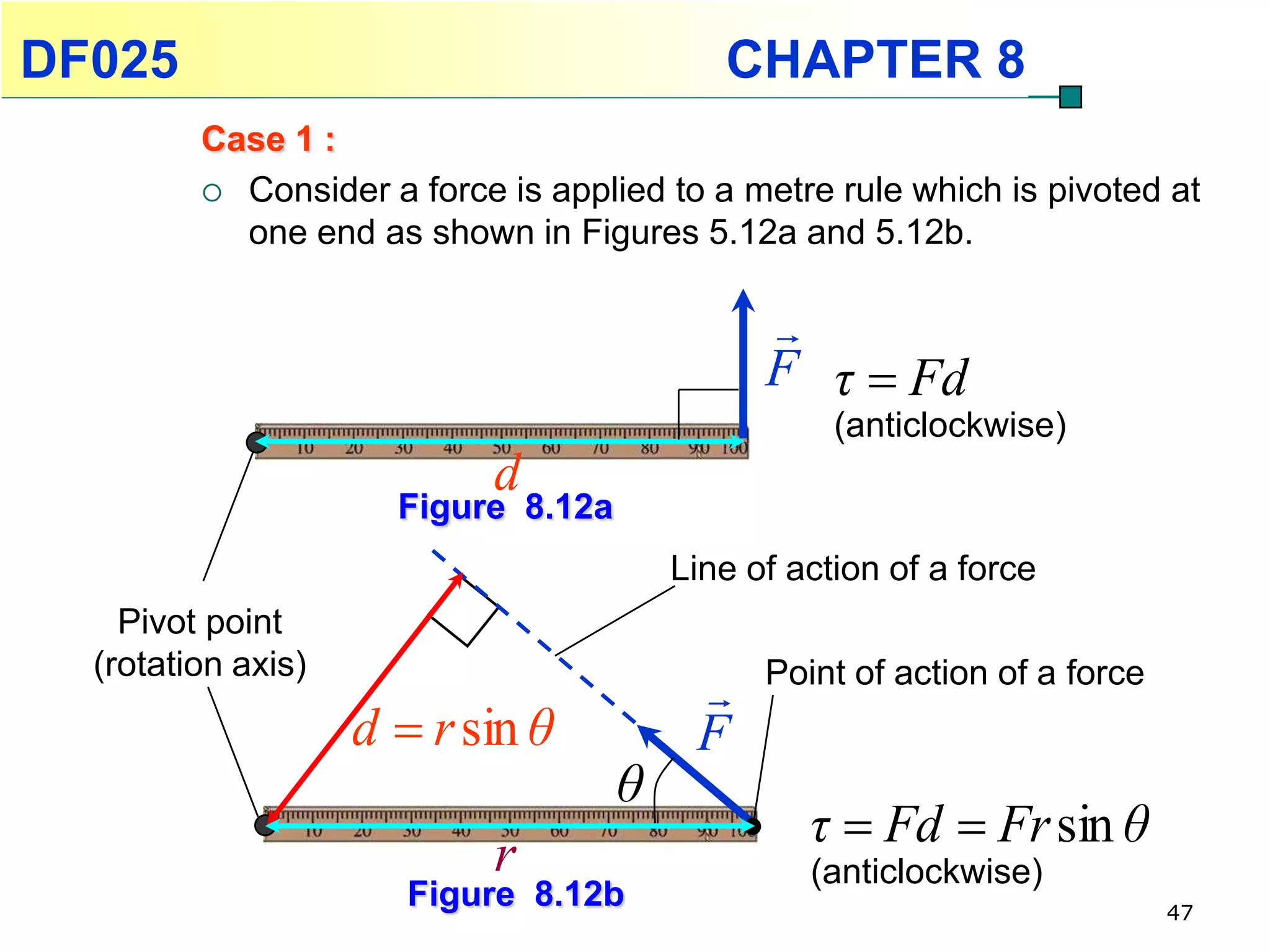
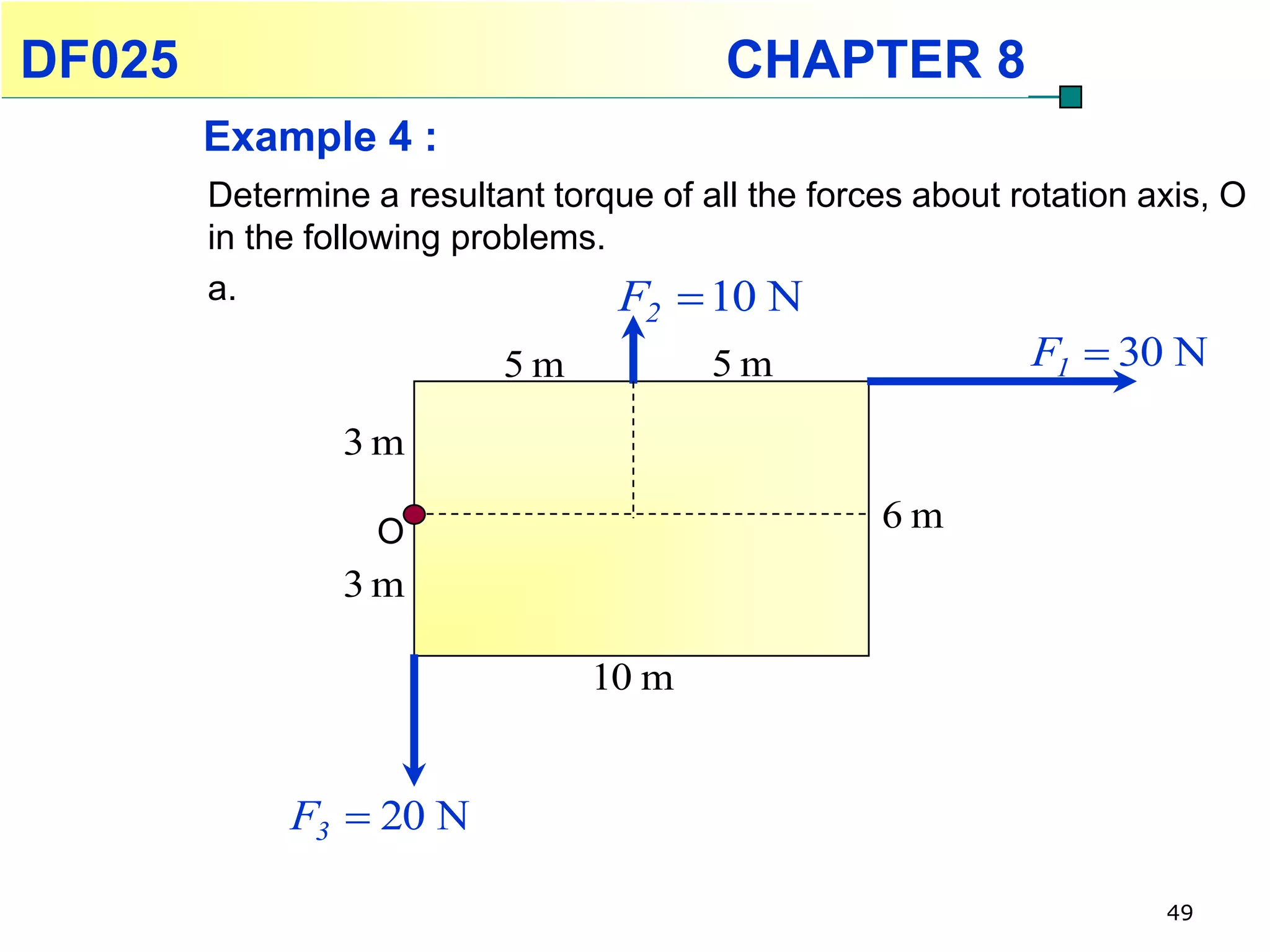
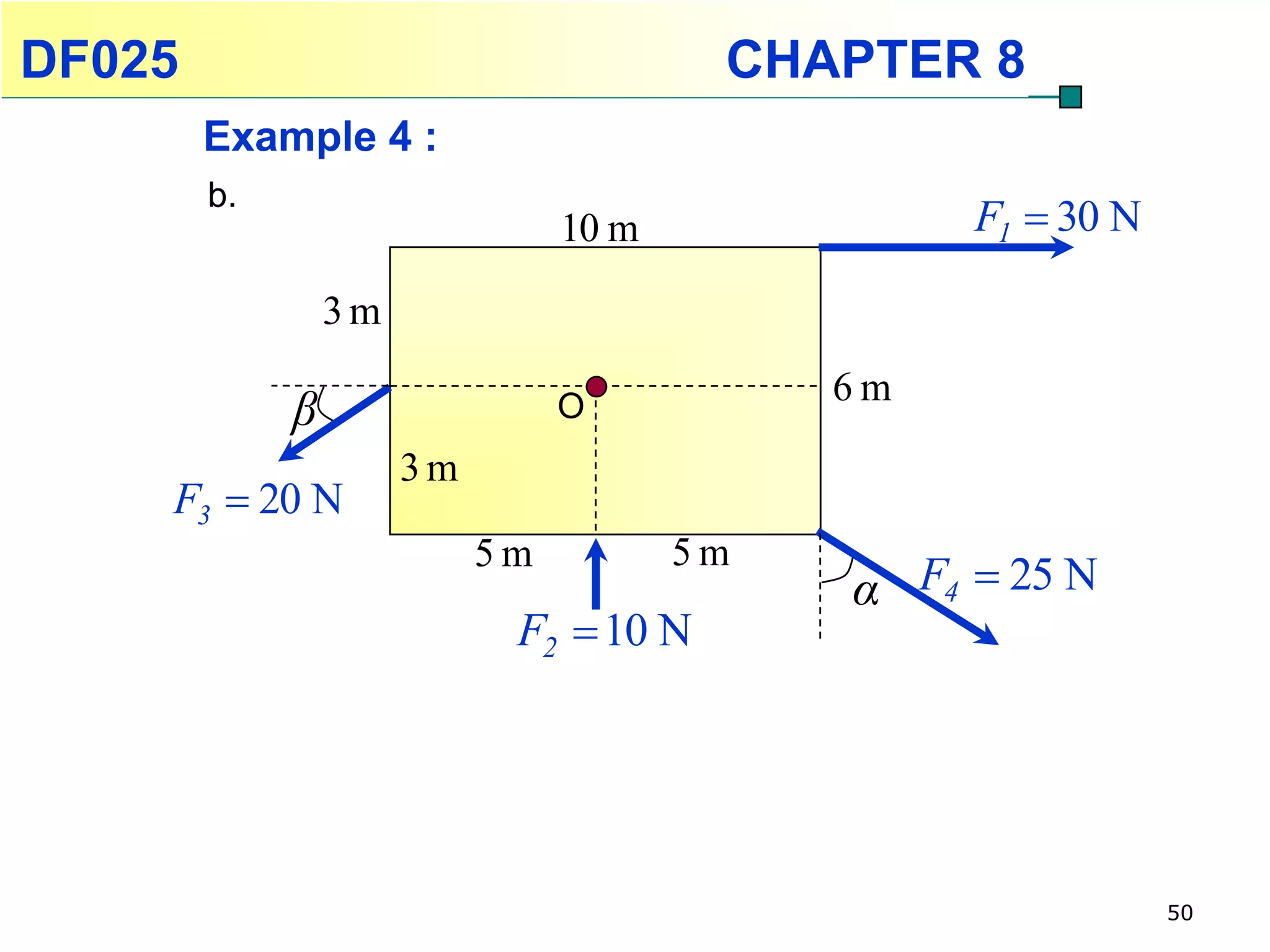
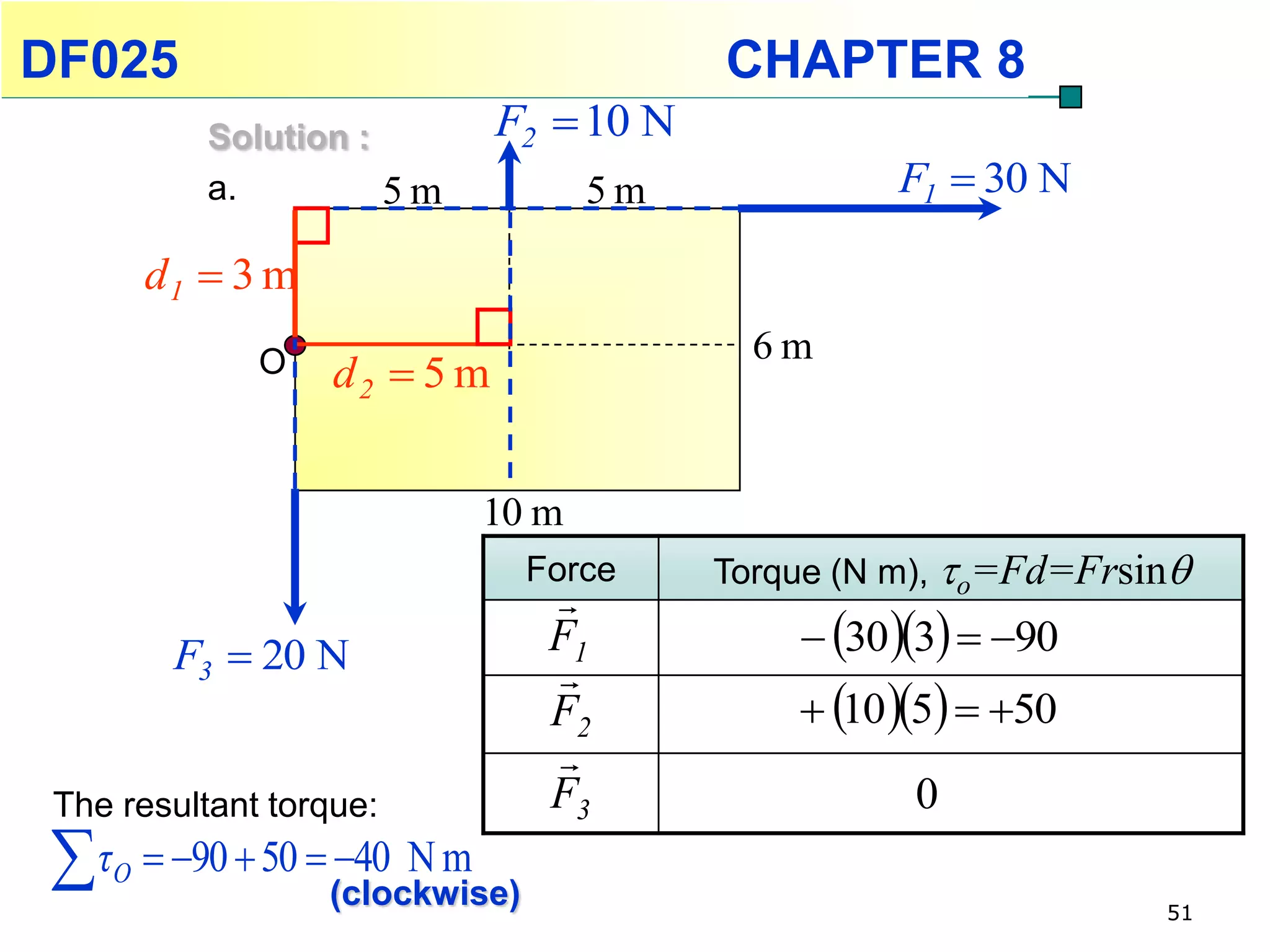
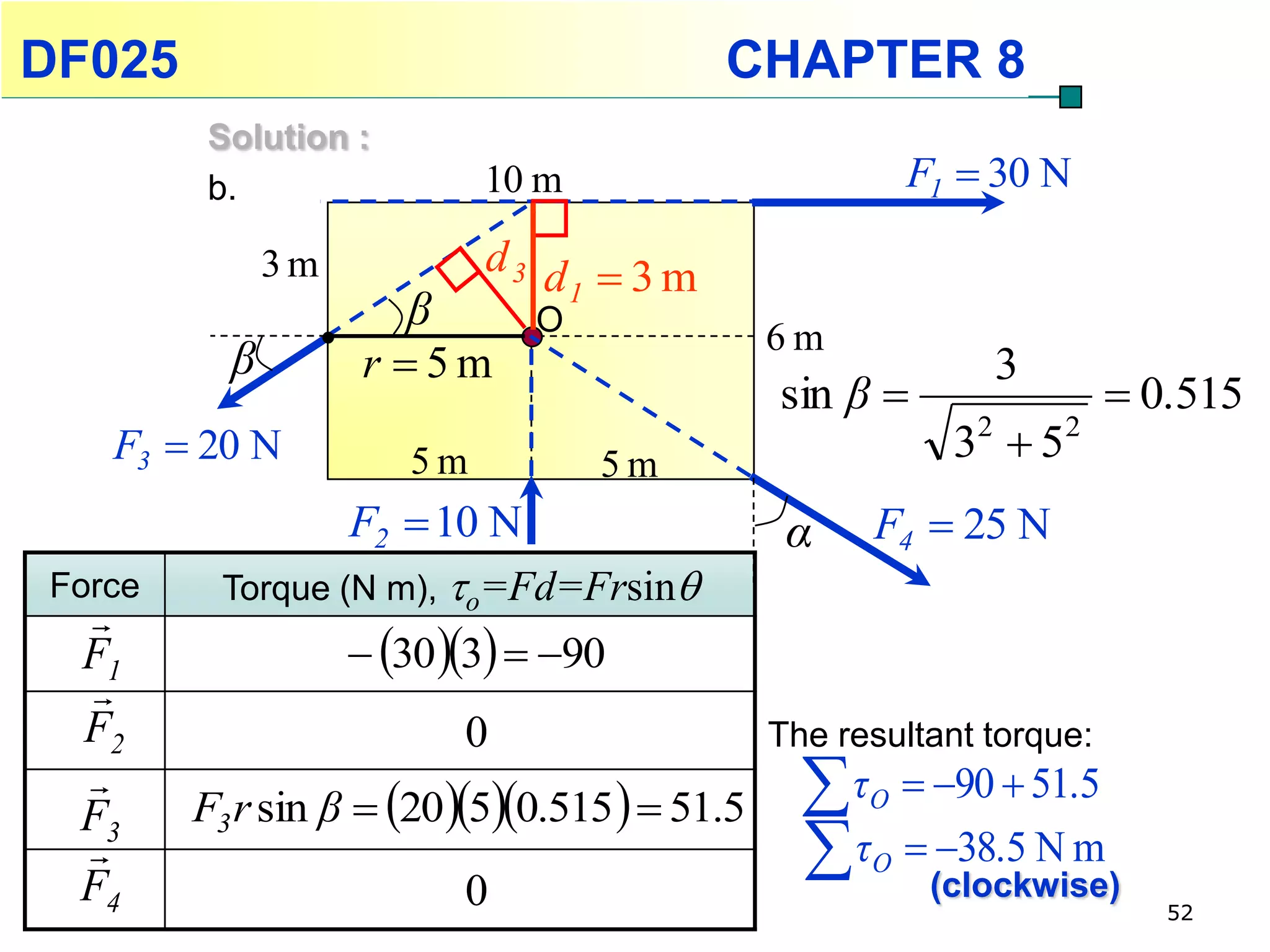
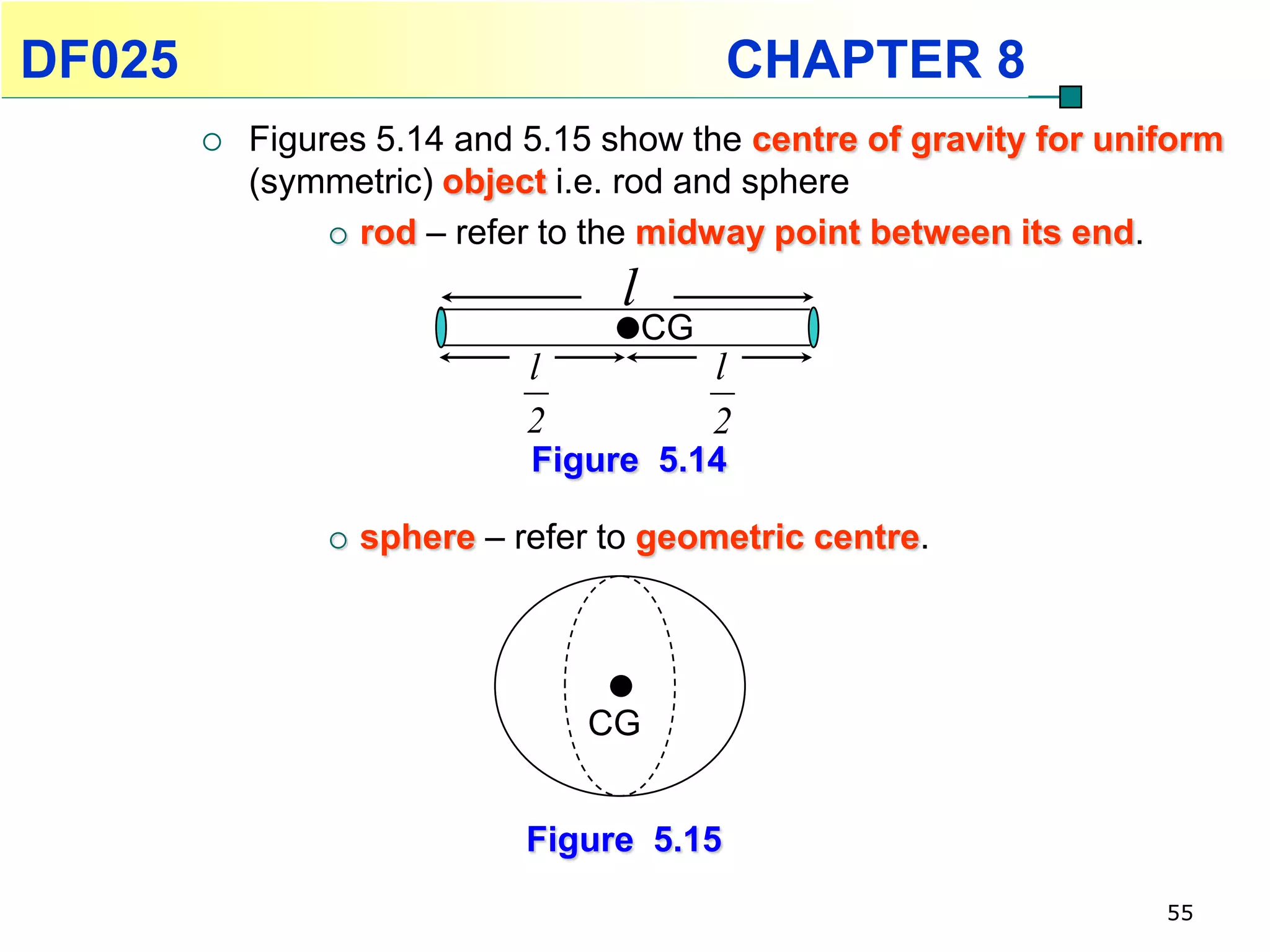
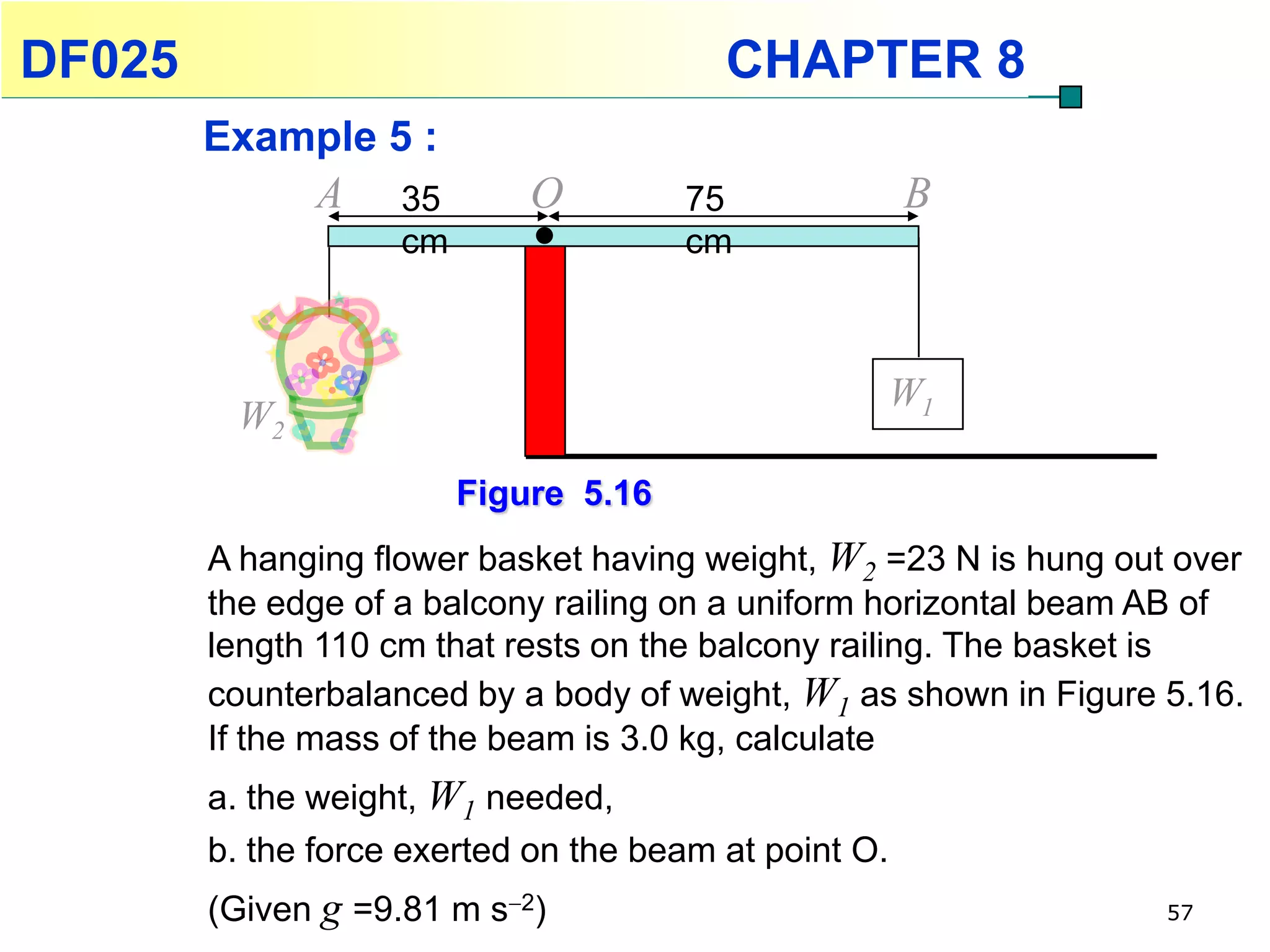
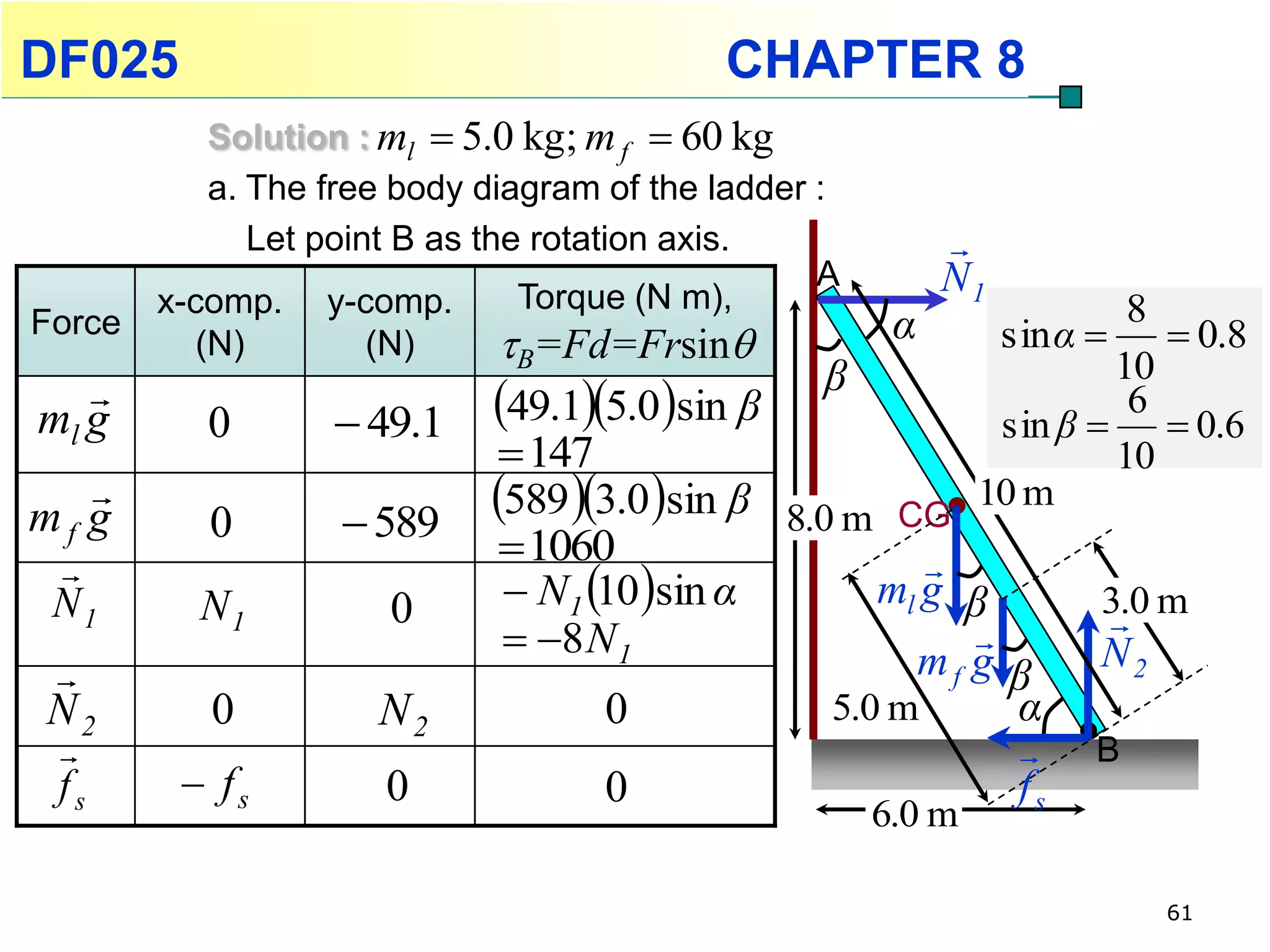
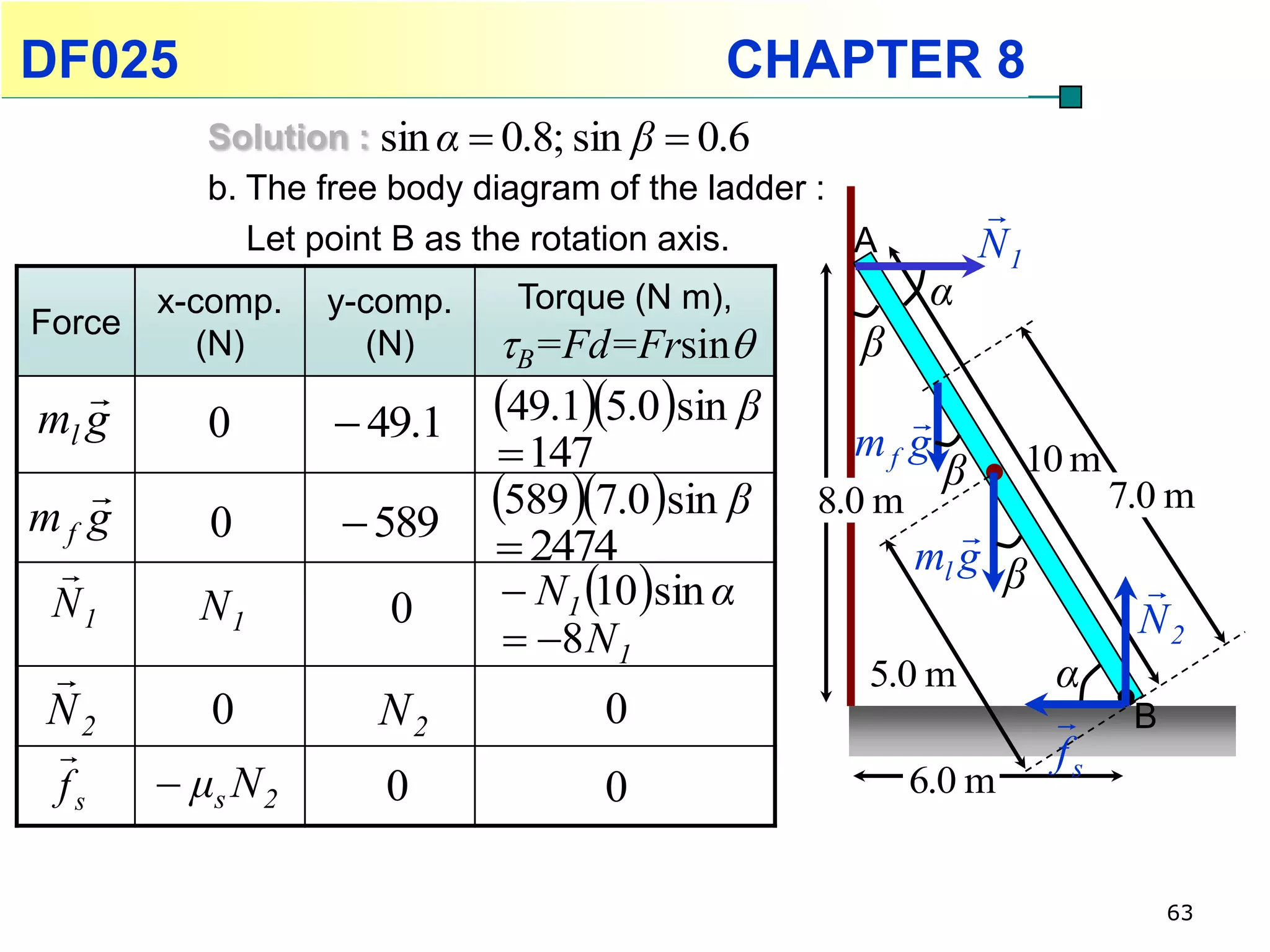
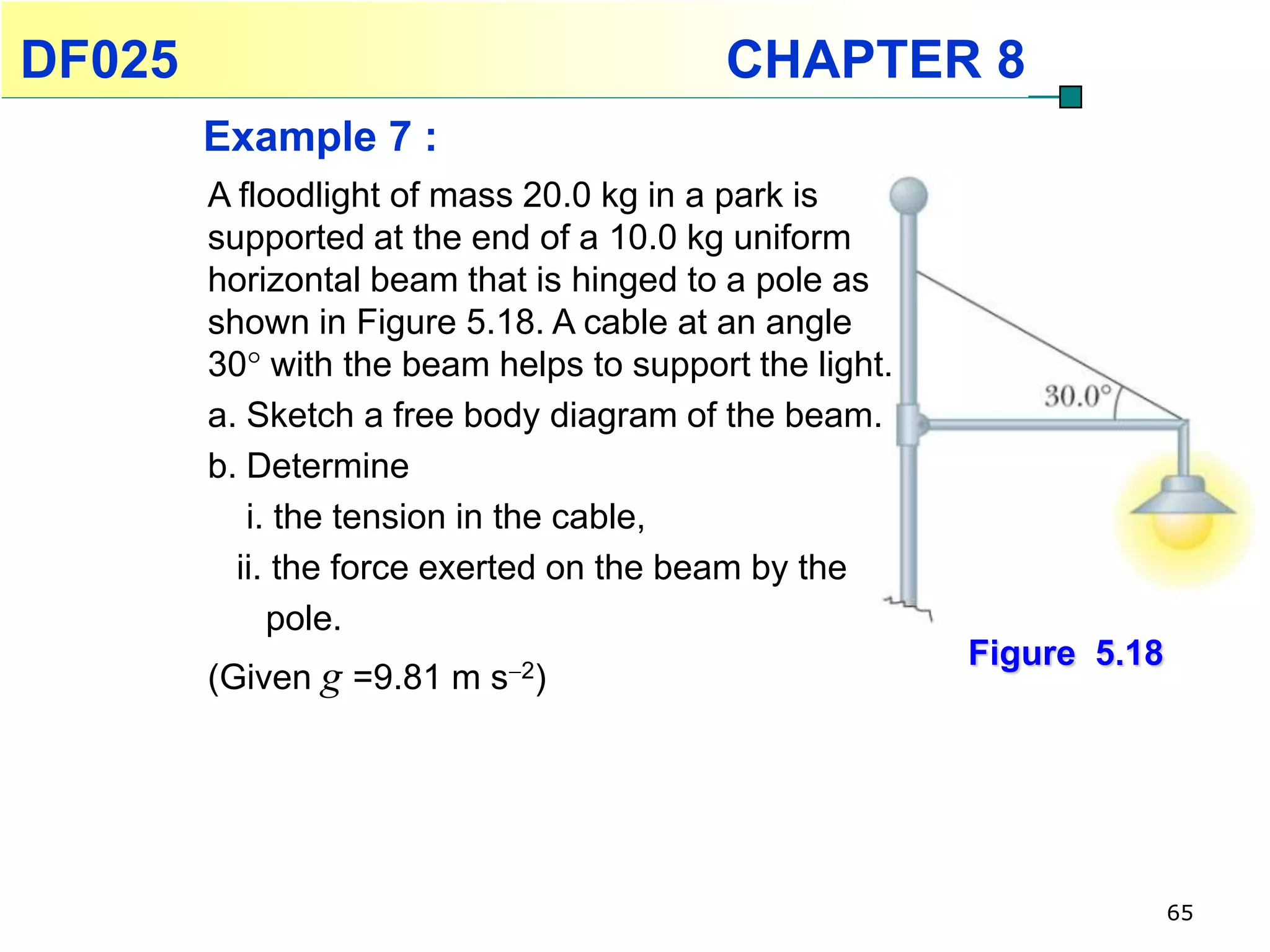
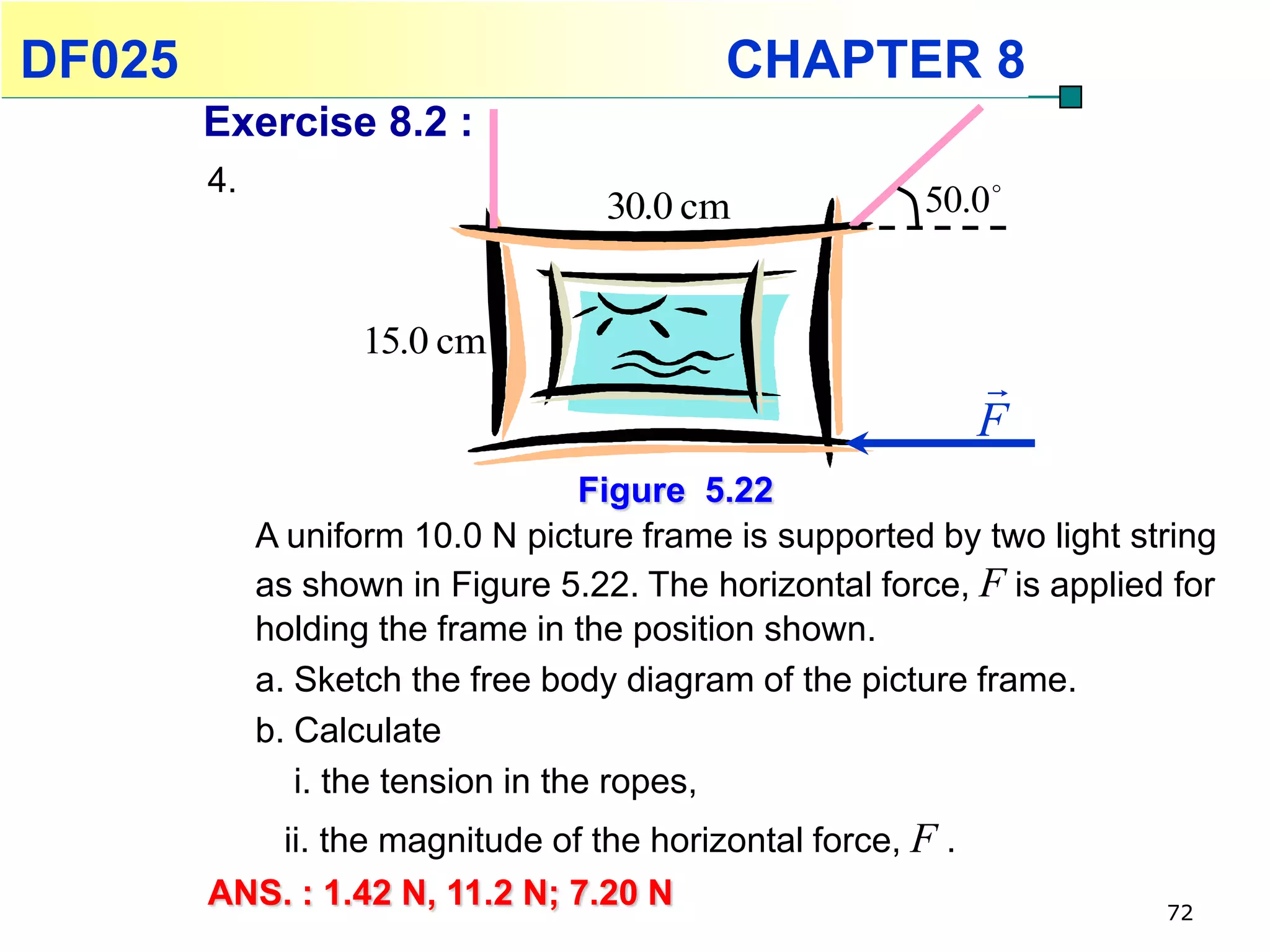
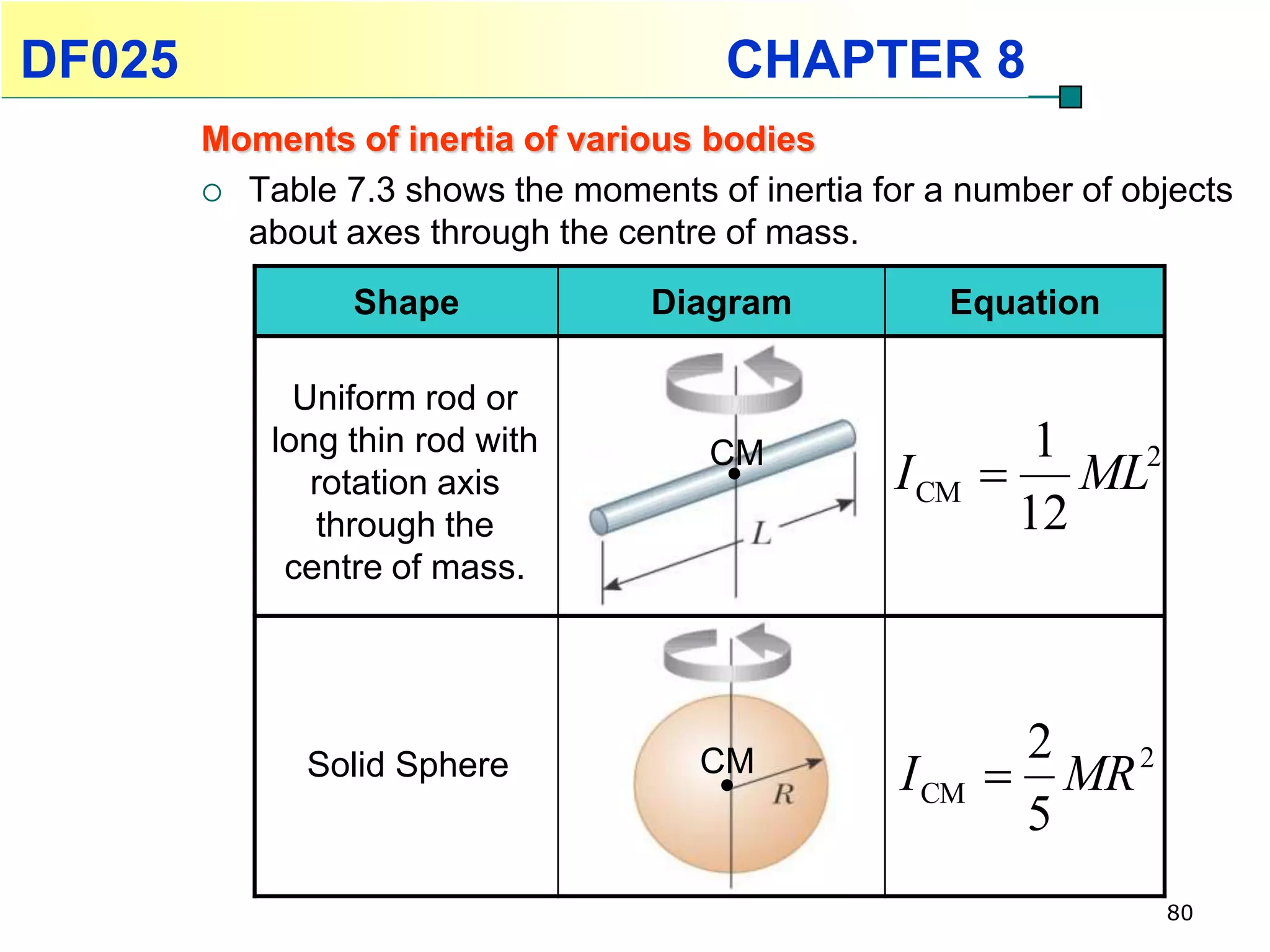
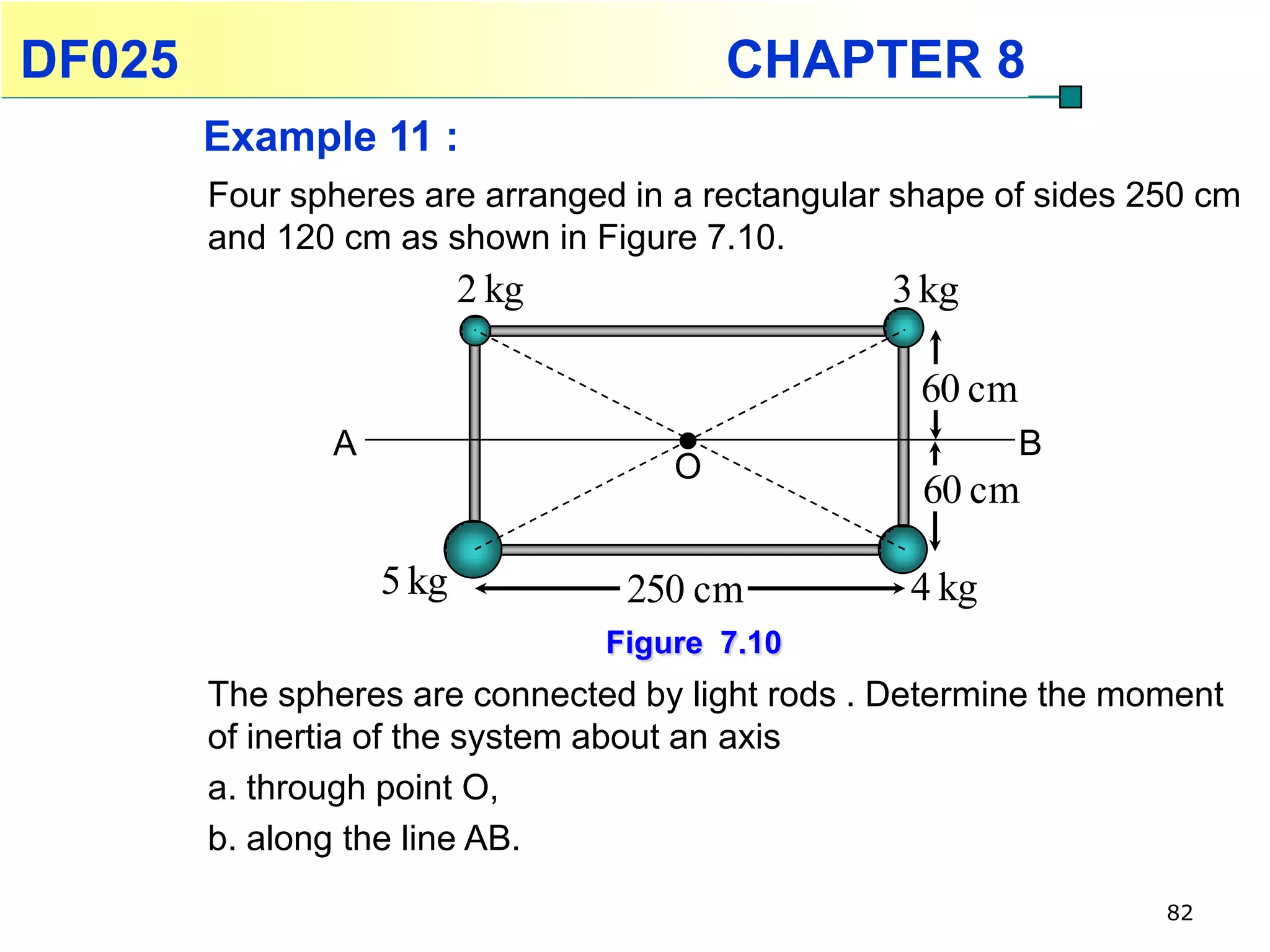
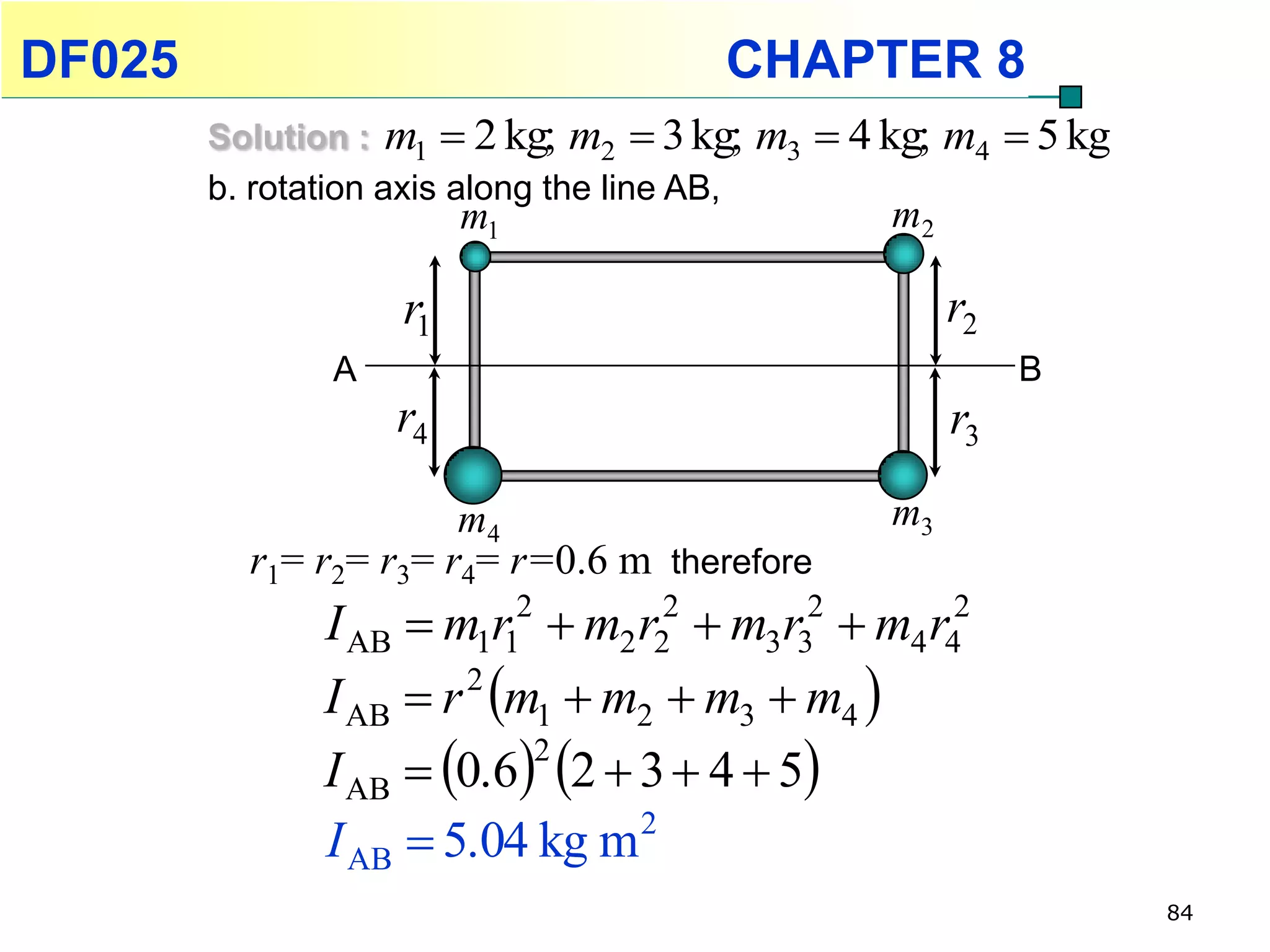
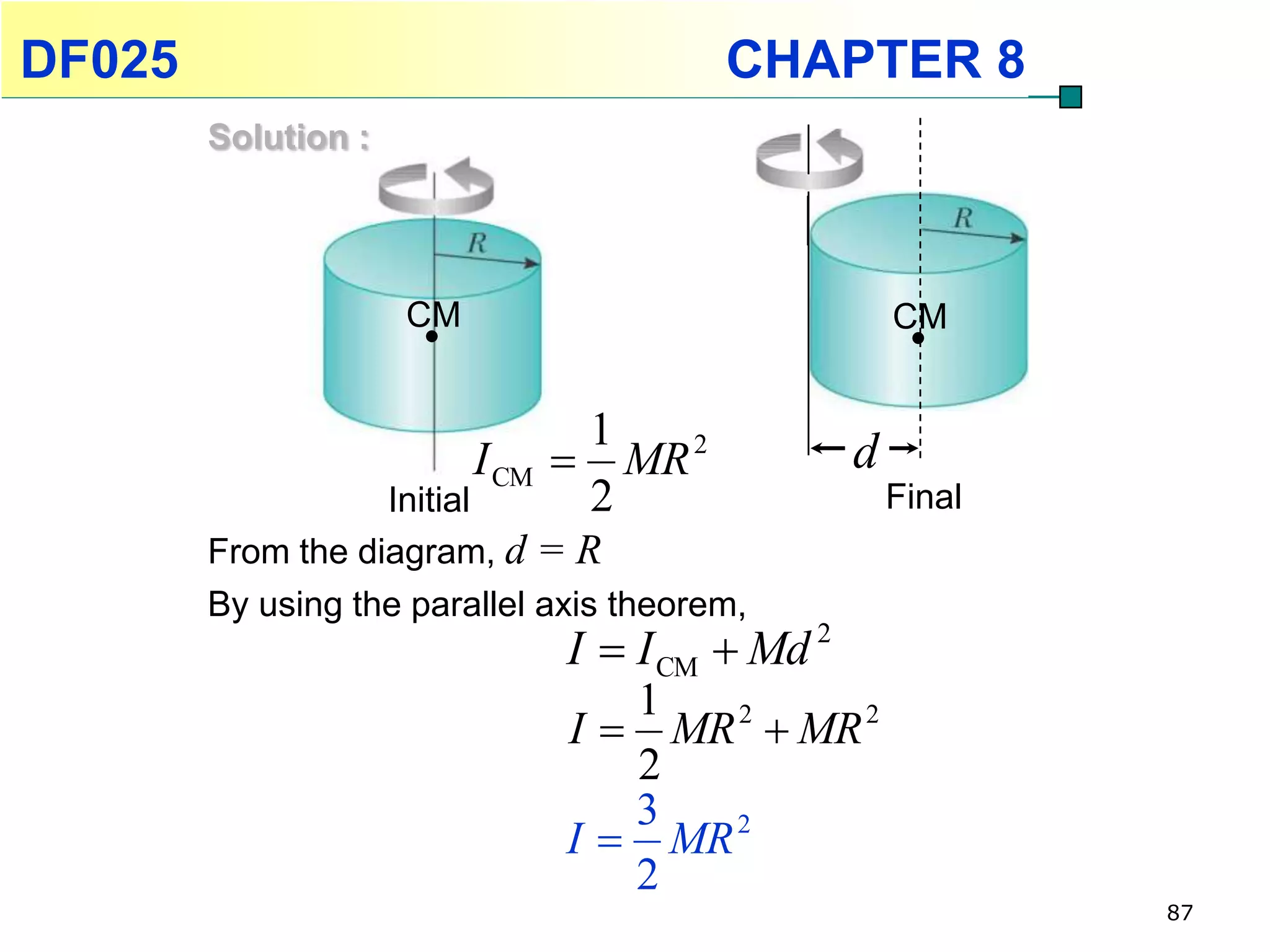
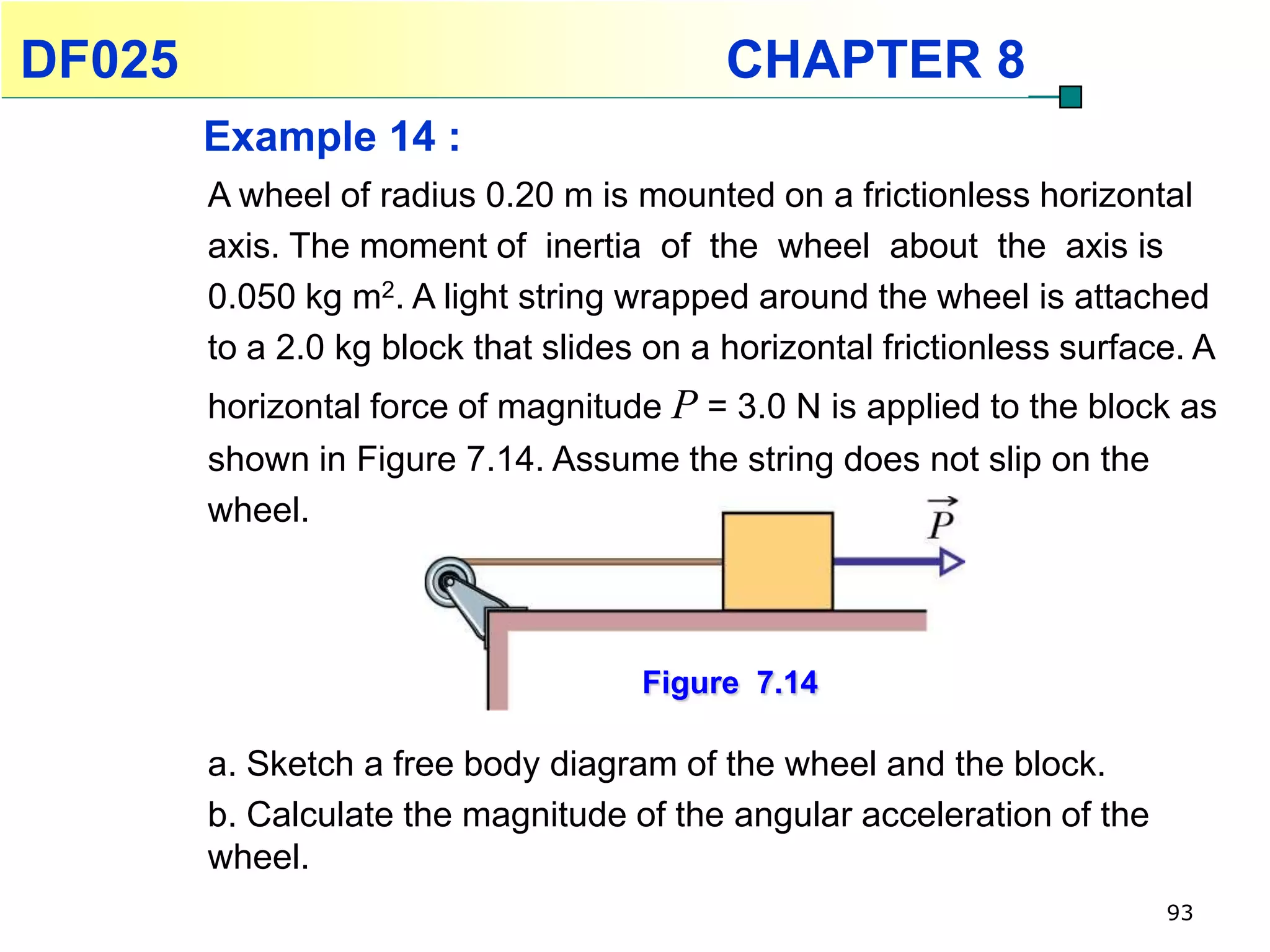
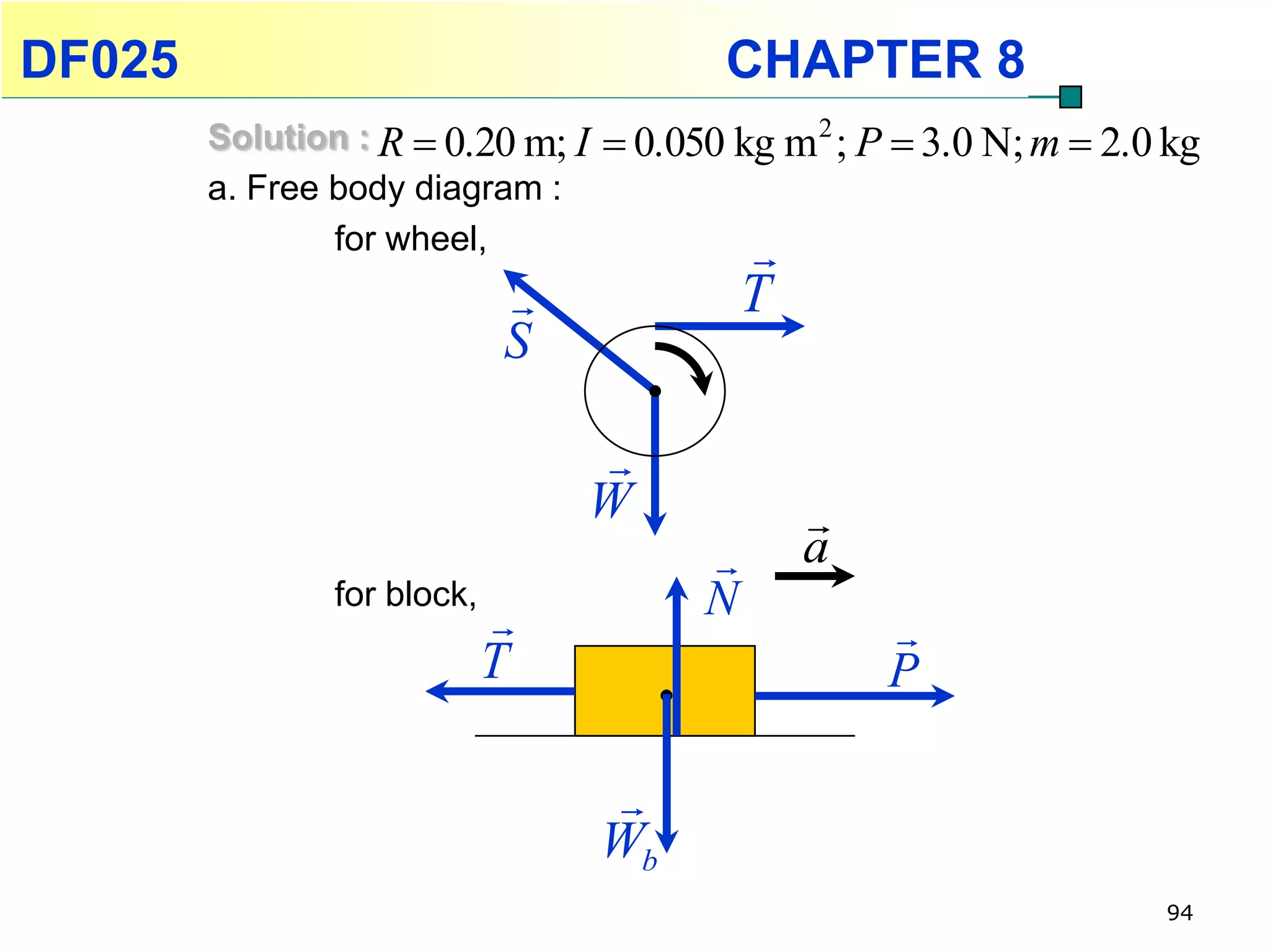
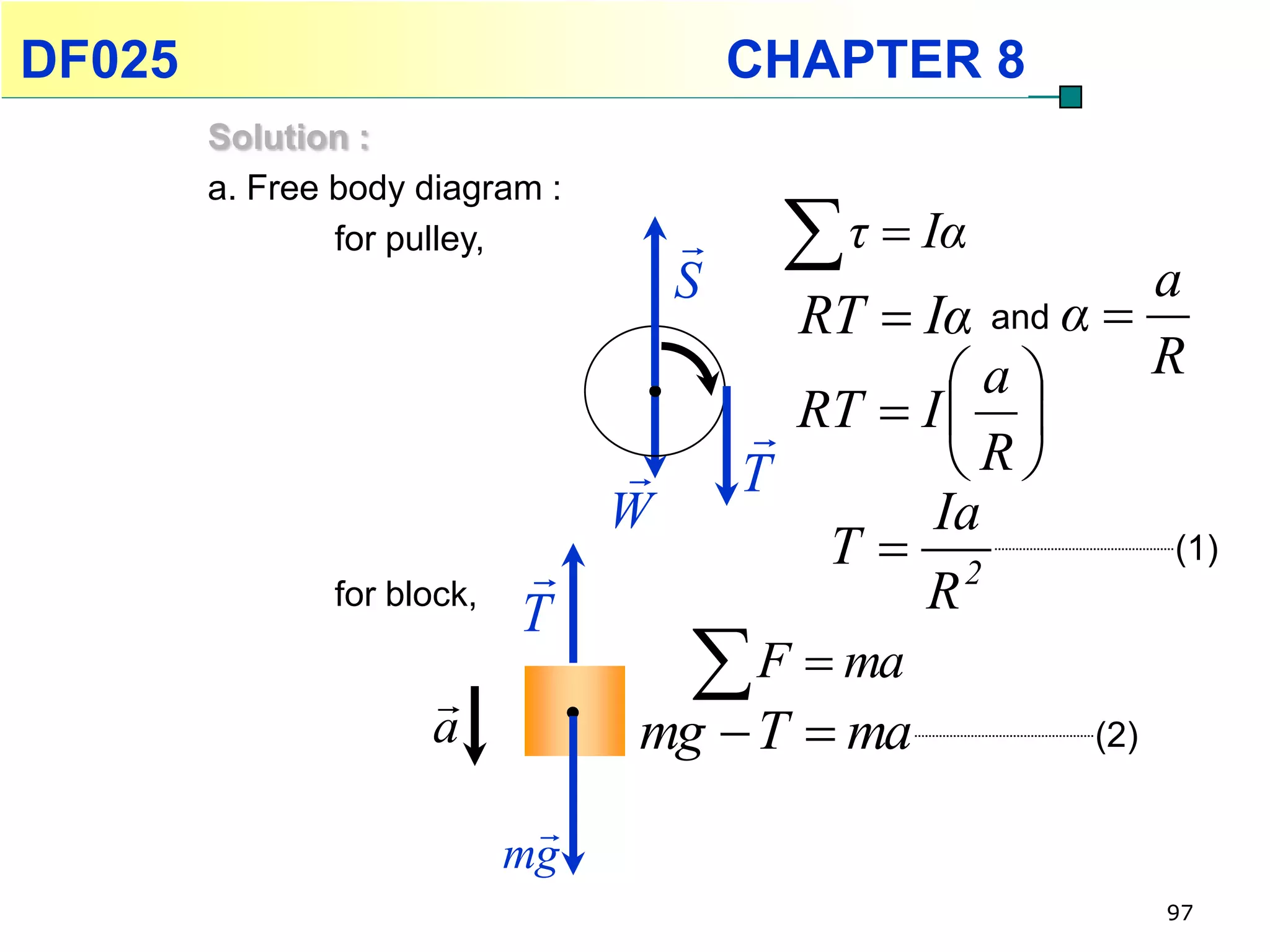
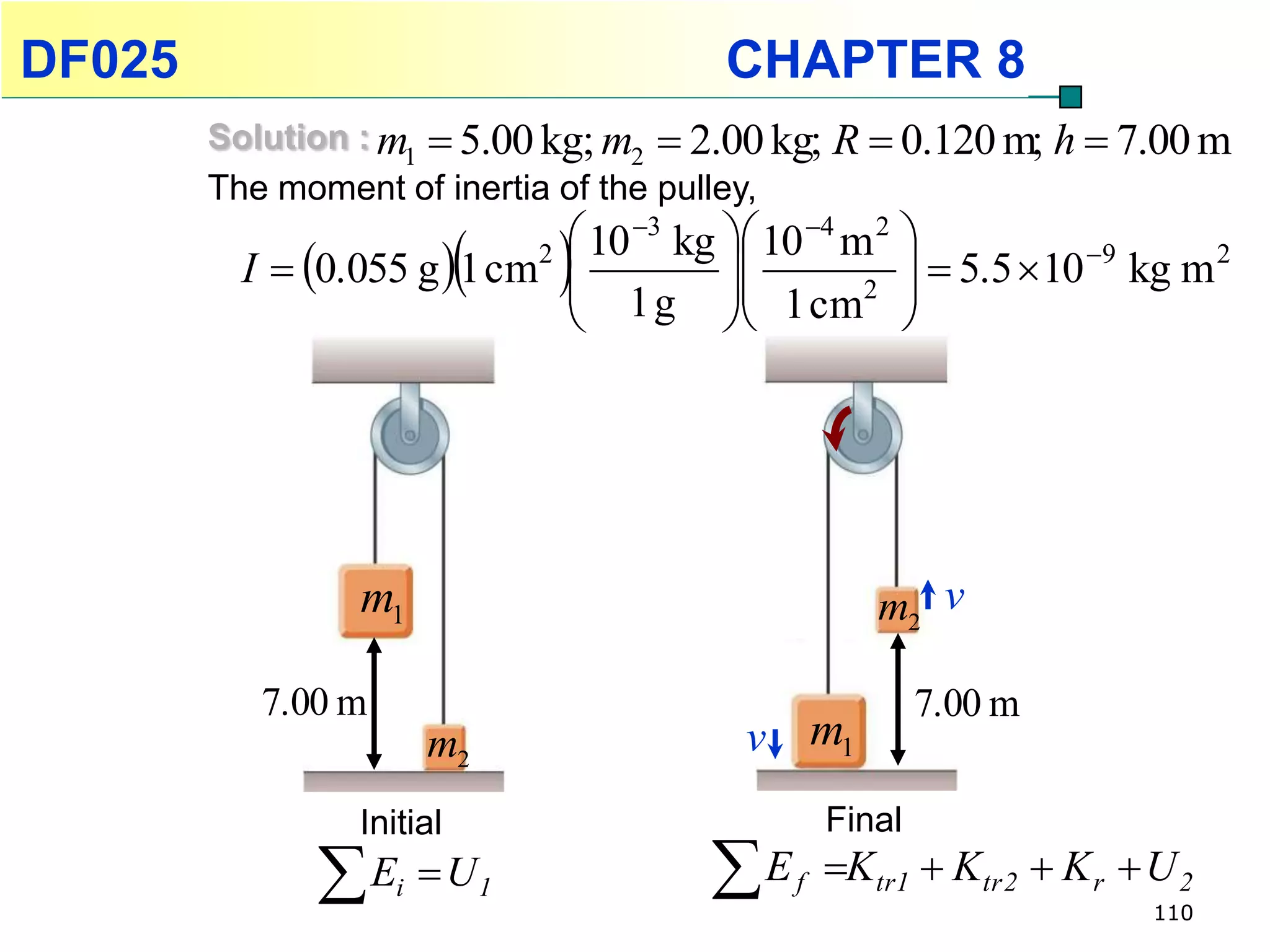
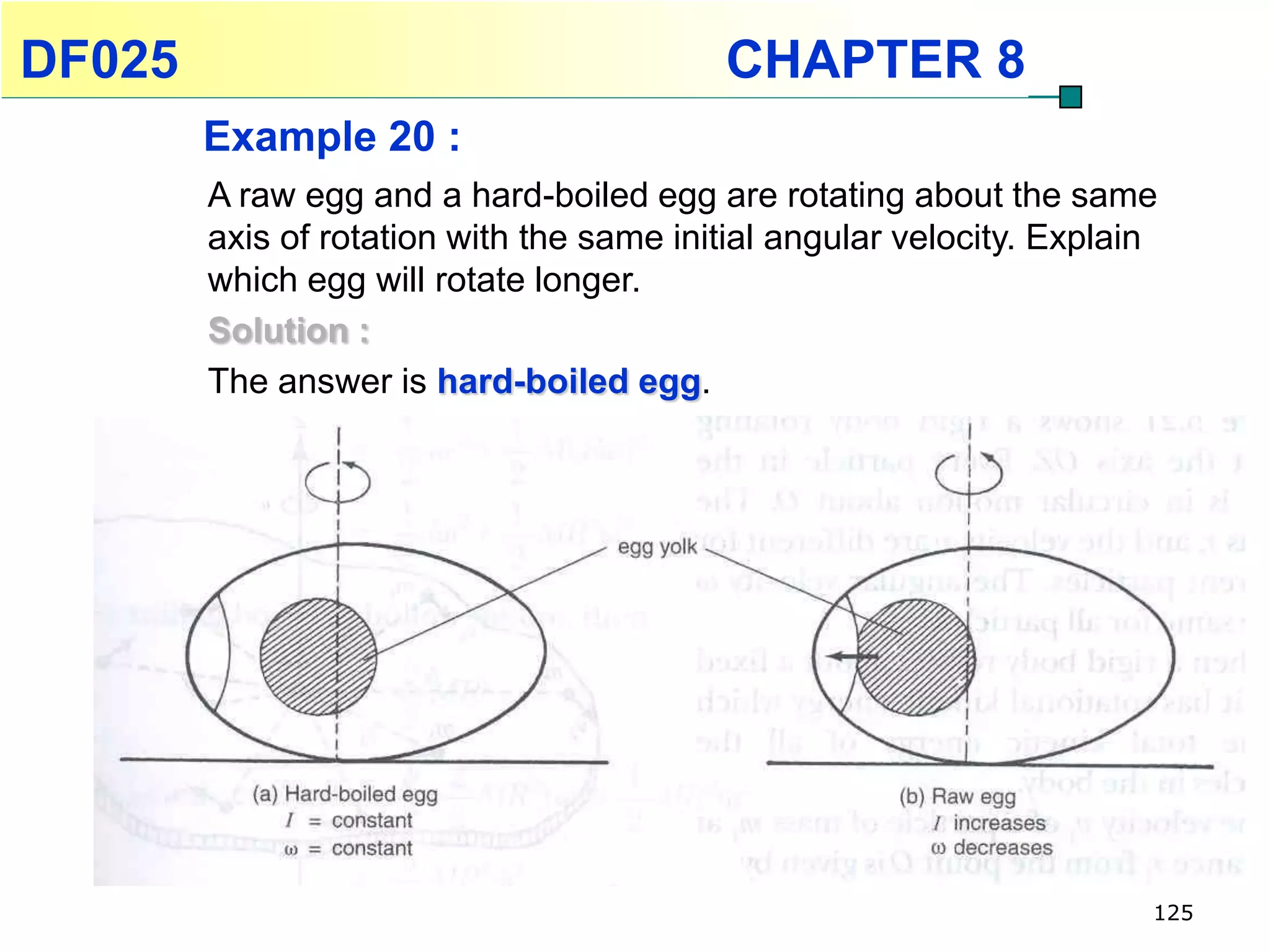
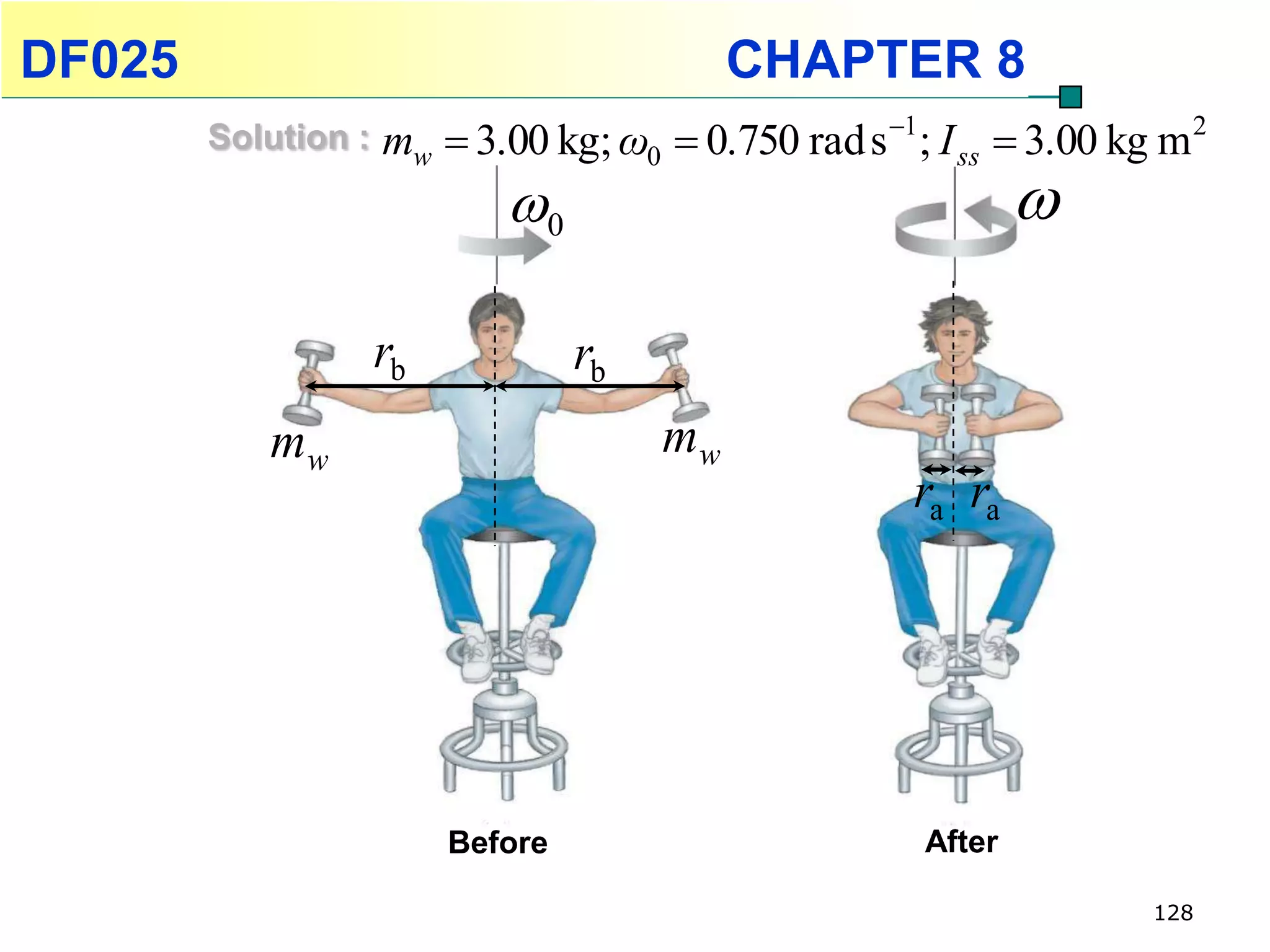
This chapter discusses rotational kinematics and the relationships between linear and rotational motion. Key concepts covered include angular displacement, velocity, and acceleration and how to define and calculate them. Equations are provided relating rotational parameters like displacement, velocity, and acceleration to their linear motion counterparts using variables like radius and arc length. Examples are given calculating values for various rotational motion situations. The chapter aims to help students understand and apply concepts of rotational kinematics.

1. DF015 CHAPTER 8
CHAPTER 8:
Rotation of a rigid body
(8 Hours)
1

2. DF025 CHAPTER 8
Learning Outcome:
8.1 Rotational kinematics (2 hours)
At the end of this chapter, students should be able to:
a) Define and use:
 angular displacement ()
 average angular velocity (av)
 instantaneous angular velocity ()
 average angular acceleration (av)
 instantaneous angular acceleration ().
2

3. DF025 CHAPTER 8
b) Relate parameters in rotational motion with their
corresponding quantities in linear motion. Write and use;
v2
s  rθ ; v  r; at  r ; ac  r 2 
r
c) Use equations for rotational motion with constant angular
acceleration;
1
, θ  ω t  t 2, ω2  ω 2  2αθ .
ω  ω  αt
0 0 0
2
3

4. DF025 CHAPTER 8
8.1 Rotational kinematics
a)(i) Angular displacement,
 is defined as an angle through which a point or line has
been rotated in a specified direction about a specified axis.
 The S.I. unit of the angular displacement is radian (rad).
 Figure 7.1 shows a point P on a rotating compact disc (CD)
moves through an arc length s on a circular path of radius r
about a fixed axis through point O.
Figure 7.1
4

5. DF025 CHAPTER 8
 From Figure 7.1, thus
s
θ OR s  rθ
r
where θ : angle (angular displaceme nt) in radian
s : arc length
r : radiusof the circle
 Others unit for angular displacement is degree () and
revolution (rev).
 Conversion factor :
1 rev  2π rad  360 
 Sign convention of angular displacement :
 Positive – if the rotational motion is anticlockwise.
 Negative – if the rotational motion is clockwise.
5

6. DF025 CHAPTER 8
a)(ii)(iii) Angular velocity
Average angular velocity, av
 is defined as the rate of change of angular displacement.
 Equation :
θ2  θ1 θ
ωav  
t 2  t1 t
whereθ2 : final angular displaceme nt in radian
θ1 : initial angular displaceme nt in radian
t : time interval
Instantaneous angular velocity, 
 is defined as the instantaneous rate of change of angular
displacement.
 Equation :
θ dθ
  limit 
t 0 t dt
6

7. DF025 CHAPTER 8
 It is a vector quantity.
 The unit of angular velocity is radian per second (rad s-1)
 Others unit is revolution per minute (rev min1 or rpm)
 Conversion factor:
2 1 
1 rpm  rad s  rad s 1
60 30
 Note :
 Every part of a rotating rigid body has the same angular
velocity.
Direction of the angular velocity
 Its direction can be determine by using right hand grip rule
where
Thumb : direction of angular velocity
Curl fingers : direction of rotation
7

8. DF025 CHAPTER 8
 Figures 7.2 and 7.3 show the right hand grip rule for determining
the direction of the angular velocity.


Figure 7.2


Figure 7.3
8

9. DF025 CHAPTER 8
Example 1 :
The angular displacement, of the wheel is given by
θ  5t 2  t
where  in radians and t in seconds. The diameter of the wheel is
0.56 m. Determine
a. the angle,  in degree, at time 2.2 s and 4.8 s,
b. the distance that a particle on the rim moves during that time
interval,
c. the average angular velocity, in rad s1 and in rev min1 (rpm),
between 2.2 s and 4.8 s,
d. the instantaneous angular velocity at time 3.0 s.
9

10. DF025 CHAPTER 8
d 0.56
Solution : r   0.28 m
2 2
a. At time, t1 =2.2 s :
θ1  52.2  2.2
2
θ1  22 rad
 180  
θ1  22 rad    1261
 π rad 
 
At time, t2 =4.8 s :
θ2  54.8  4.8
2
θ2  110 rad
 180  
θ2  110 rad    6303 
 π rad 
 
10

11. DF025 CHAPTER 8
d 0.56
Solution : r   0.28 m
2 2
b. By applying the equation of arc length,
s  rθ
Therefore s  r  r 2  1 
s  0.28110  22 
s  24.6 m
c. The average angular velocity in rad s1 is given by
θ 2  1 
ωav  
t t2  t1 
ωav 
110  22 
4.8  2.2
ωav  33.9 rad s 1
11

12. DF025 CHAPTER 8
Solution :
c. and the average angular velocity in rev min1 is
 33.9 rad  1 rev  60 s 
ωav     
 1 s  2 rad  1 min 
ωav  324 rev min 1 OR 324 rpm
d. The instantaneous angular velocity as a function of time is
dθ
ω
dt
ω
dt

d 2
5t  t 
ω  10t  1
ω  103.0  1
At time, t =3.0 s :
ω  29 rad s 1
12

13. DF025 CHAPTER 8
Example 2 :
A diver makes 2.5 revolutions on the way down from a 10 m high
platform to the water. Assuming zero initial vertical velocity,
calculate the diver’s average angular (rotational) velocity during a
dive.
(Given g = 9.81 m s2)
Solution :
uy  0
θ0  0
10 m
θ1  2.5 rev
water
13

14. DF025 CHAPTER 8
Solution : θ1  2.5  2π  5π rad
From the diagram, s y  10 m
Thus 1
s y  u y t  gt 2
2
 10  0  9.81t 2
1
2
t  1.43 s
Therefore the diver’s average angular velocity is
θ1  θ0
ωav 
t
5π  0
ωav 
1.43
ωav  11.0 rad s 1
14

15. DF025 CHAPTER 8
a)(iv)(v) Angular acceleration
Average angular acceleration, av
 is defined as the rate of change of angular velocity.
 Equation :
ω2  ω1 ω
 av  
t 2  t1 t
where ω2 : final angular velocity
ω1 : initial angular velocity
t : time interval
Instantaneous angular acceleration, 
 is defined as the instantaneous rate of change of angular
velocity.
 Equation :
ω dω
α  limit 
t 0 t dt
15

16. DF025 CHAPTER 8
 It is a vector quantity.
 The unit of angular acceleration is rad s2.
 Note:
 If the angular acceleration,  is positive, then the angular
velocity,  is increasing.
If the angular acceleration,  is negative, then the angular
velocity,  is decreasing.
Direction of the angular acceleration
 If the rotation is speeding up,  and  in the same direction
as shown in Figure 7.4. 
 α

Figure 7.4
16

17. DF025 CHAPTER 8
 If the rotation is slowing down,  and  have the opposite
direction as shown in Figure 7.5.

 α

Figure 7.5
Example 3 :
The instantaneous angular velocity,  of the flywheel is given
by
ω  8t 3  t 2
where  in radian per second and t in seconds.
Determine
a. the average angular acceleration between 2.2 s and 4.8 s,
b. the instantaneous angular acceleration at time, 3.0 s.
17

18. DF025 CHAPTER 8
Solution :
a. At time, t1 =2.2 s :
ω1  82.2  2.2
3 2
ω1  80.3 rad s 1
At time, t2 =4.8 s :
ω2  84.8  4.8
3 2
ω2  862 rad s 1
Therefore the average angular acceleration is
ω2  ω1
αav 
t 2  t1
862  80.3
αav 
4.8  2.2
αav  301 rad s 2
18

19. DF025 CHAPTER 8
Solution :
b. The instantaneous angular acceleration as a function of time is
dω
α
dt
α
dt

d 3 2
8t  t 
α  24t 2  2t
At time, t =3.0 s :
α  243.0  23.0
2
α  210 rad s 2
19

20. DF025 CHAPTER 8
Exercise 8.1a :
1. If a disc 30 cm in diameter rolls 65 m along a straight line
without slipping, calculate
a. the number of revolutions would it makes in the process,
b. the angular displacement would be through by a speck of
gum on its rim.
ANS. : 69 rev; 138 rad
2. During a certain period of time, the angular displacement of a
swinging door is described by
θ  5.00  10.0t  2.00t 2
where  is in radians and t is in seconds. Determine the angular
displacement, angular speed and angular acceleration
a. at time, t =0,
b. at time, t =3.00 s.
ANS. : 5.00 rad, 10.0 rad s1, 4.00 rad s2; 53.0 rad, 22.0 rad s1,
4.00 rad s2 20

21. DF025 CHAPTER 8
Learning Outcome:
8.1.b) Relationship between linear and rotational
motion (½ hour)
At the end of this chapter, students should be able to:
 Relate parameters in rotational motion with their
corresponding quantities in linear motion. Write and use;
v2
s  rθ ; v  r; at  r ; ac  r 2 
r
21

22. DF025 CHAPTER 8
8.1.b) Relationship between linear and
rotational motion
Relationship between linear velocity, v and
angular velocity, 
 When a rigid body is rotates about rotation axis O , every
particle in the body moves in a circle as shown in the Figure 7.6.
y

v
P
r s
 x
O
Figure 8.6
22

23. DF025 CHAPTER 8
 Point P moves in a circle of radius r with the tangential velocity
v where its magnitude is given by
ds
v and s  rθ
dt
d
vr
dt
v  r
 The direction of the linear (tangential) velocity always
tangent to the circular path.
 Every particle on the rigid body has the same angular speed
(magnitude of angular velocity) but the tangential speed is not
the same because the radius of the circle, r is changing
depend on the position of the particle.
Simulation 8.1
23

24. DF025 CHAPTER 8
Relationship between tangential acceleration, at and
angular acceleration, 
 If the rigid body is gaining the angular speed then the
tangential velocity of a particle also increasing thus two
component of acceleration are occurred as shown in
Figure 7.7.
y

at
 P
a 
ac
O
x
Figure 8.7
24

25. DF025 CHAPTER 8
 The components are tangential acceleration, at and
centripetal acceleration, ac given by
dv
at  and v  rω
dt
d
at  r at  r
dt
v2
but ac   r  v2
r
 The vector sum of centripetal and tangential acceleration of
a particle in a rotating body is resultant (linear) acceleration, a
given by   
a  at  ac Vector form

and its magnitude,
a  at  ac
2 2
25

26. DF025 CHAPTER 8
Learning Outcome:
8.1.c) Rotational motion with uniform angular
acceleration (1/2 hour)
At the end of this chapter, students should be able to:
 Write and use equations for rotational motion with
constant angular acceleration;
ω  ω0  αt
1 2
θ  ω0 t  t
2
ω2  ω0  2αθ
2
26

27. DF025 CHAPTER 8
8.1.c) Rotational motion with uniform
angular acceleration
 Table 8.1 shows the symbols used in linear and rotational
kinematics.
Linear Rotational
Quantity
motion motion
s Displacement θ
u Initial velocity ω0
v Final velocity ω
a Acceleration α
t Time t
Table 8.1
27

28. DF025 CHAPTER 8
 Table 8.2 shows the comparison of linear and rotational motion
with constant acceleration.
Linear motion Rotational motion
a  constant α  constant
v  u  at ω  ω0  αt
1 2 1 2
s  ut  at θ  ω0 t  αt
2 2
v 2  u 2  2as ω  2
ω0
2
 2αθ
s  v  u t
1
θ  ω  ω0 t
1
2 2
where  in radian. Table 8.2
28

29. DF025 CHAPTER 8
Example 4 :
A car is travelling with a velocity of 17.0 m s1 on a straight
horizontal highway. The wheels of the car has a radius of 48.0 cm.
If the car then speeds up with an acceleration of 2.00 m s2 for
5.00 s, calculate
a. the number of revolutions of the wheels during this period,
b. the angular speed of the wheels after 5.00 s.
Solution : u  17.0 m s 1 , r  0.48 m, a  2.00 m s 2 , t  5.00 s
a. The initial angular velocity is
u  rω0
1
17.0  0.48ω0 ω0  35.4 rad s
and the angular acceleration of the wheels is given by
a  rα
2.00  0.48α α  4.17 rad s 2
29

30. DF025 CHAPTER 8
Solution : u  17.0 m s 1 , r  0.48 m, a  2.00 m s 2 , t  5.00 s
a. By applying the equation of rotational motion with constant
angular acceleration, thus
1 2
θ  ω0 t  αt
2
θ  35.4 5.00   4.17 5.00 
1 2
2
θ  229 rad
therefore  1 rev 
θ  229 rad    36.5 rev
 2π rad 
b. The angular speed of the wheels after 5.00 s is
ω  ω0  αt
ω  35.4  4.17 5.00 
ω  56.3 rad s 1
30

31. DF025 CHAPTER 8
Example 5 :
The wheels of a bicycle make 30 revolutions as the bicycle
reduces its speed uniformly from 50.0 km h-1 to 35.0 km h-1. The
wheels have a diameter of 70 cm.
a. Calculate the angular acceleration.
b. If the bicycle continues to decelerate at this rate, determine the
time taken for the bicycle to stop.
0.70
Solution : θ  30  2π  60π rad, r   0.35 m,
2
50.0 km  10 3 m  1 h 
u   1
  13.9 m s ,
1 h  1 km  3600 s 
 
35.0 km  10 3 m  1 h 
v     9.72 m s
1
1 h  1 km  3600 s 
 
31

32. DF025 CHAPTER 8
Solution :
a. The initial angular speed of the wheels is
u  rω0
13.9  0.35ω0 ω0  39.7 rad s 1
and the final angular speed of the wheels is
v  rω
9.72  0.35ω ω  27.8 rad s 1
therefore
ω2  ω0  2αθ
2
27.8  39.7   2α60π
2 2
α  2.13 rad s 2
1
b. The car stops thus ω  0 and ω0  27.8 rad s
Hence ω  ω0  αt
0  27.8   2.13t
t  13.1 s
32

33. DF025 CHAPTER 8
Example 6 :
A blade of a ceiling fan has a radius of 0.400 m is rotating about a
fixed axis with an initial angular velocity of 0.150 rev s-1. The
angular acceleration of the blade is 0.750 rev s-2. Determine
a. the angular velocity after 4.00 s,
b. the number of revolutions for the blade turns in this time interval,
c. the tangential speed of a point on the tip of the blade at time,
t =4.00 s,
d. the magnitude of the resultant acceleration of a point on the tip
of the blade at t =4.00 s.
Solution : r  0.400 m, ω0  0.150  2π  0.300π rad s 1 ,
α  0.750  2π  1.50π rad s 2
a. Given t =4.00 s, thus
ω  ω0  αt ω  0.300π   1.50π 4.00 
1
ω  19.8 rad s
33

34. DF025 CHAPTER 8
Solution :
b. The number of revolutions of the blade is
1 2
θ  ω0 t  αt
2
θ  0.300 4.00   1.504.00 
1 2
2
θ  41.5 rad
 1 rev 
θ  41.5 rad    6.61 rev
 2π rad 
c. The tangential speed of a point is given by
v  rω
v  0.400 19.8
v  7.92 m s 1
34

35. DF025 CHAPTER 8
Solution :
d. The magnitude of the resultant acceleration is
a  ac  at
2 2
2
v 2

a    rα 2
 r 
 
 7.92 
2
2

a    0.400  1.50π 2
 0.400 
 
a  157 m s 2
35

36. DF025 CHAPTER 8
Example 7 :
Calculate the angular velocity of
a. the second-hand,
b. the minute-hand and
c. the hour-hand,
of a clock. State in rad s-1.
d. What is the angular acceleration in each case?
Solution :
a. The period of second-hand of the clock is T = 60 s, hence
2π 2π
ω ω
T 60
1
ω  0.11 rad s
36

37. DF025 CHAPTER 8
Solution :
b. The period of minute-hand of the clock is T = 60 min = 3600 s,
hence
2π
ω
3600
ω  1.74  10 3 rad s 1
c. The period of hour-hand of the clock is T = 12 h = 4.32 104 s,
hence 2π
ω
4.32  10 4
ω  1.45  10 4 rad s 1
d. The angular acceleration in each cases is zero.
37

38. DF025 CHAPTER 8
Example 8 :
A coin with a diameter of 2.40 cm is dropped on edge on a
horizontal surface. The coin starts out with an initial angular speed
of 18 rad s1 and rolls in a straight line without slipping. If the
rotation slows down with an angular acceleration of magnitude
1.90 rad s2, calculate the distance travelled by the coin before
coming to rest.
Solution : ω  18 rad s 1
0 ω  0 rad s 1
d  2.40  10 m2 α  1.90 rad s 2
s
The radius of the coin is
d
r   1.20  10 2 m
2
38

39. DF025 CHAPTER 8
Solution :
The initial speed of the point at the edge the coin is
u  rω0
 
u  1.20 10 2 18
u  0.216 m s 1
1
and the final speed is v  0 m s
The linear acceleration of the point at the edge the coin is given by
a  rα
 
a  1.20 10 2  1.90 
a  2.28  10 2 m s 2
Therefore the distance travelled by the coin is
v  u  2as
2 2

0  0.216   2  2.28 10 2 s
2

s  1.02 m
39

40. DF025 CHAPTER 8
Exercise 8.1b&c :
1. A disk 8.00 cm in radius rotates at a constant rate of 1200 rev
min-1 about its central axis. Determine
a. its angular speed,
b. the tangential speed at a point 3.00 cm from its centre,
c. the radial acceleration of a point on the rim,
d. the total distance a point on the rim moves in 2.00 s.
ANS. : 126 rad s1; 3.77 m s1; 1.26  103 m s2; 20.1 m
2. A 0.35 m diameter grinding wheel rotates at 2500 rpm.
Calculate
a. its angular velocity in rad s1,
b. the linear speed and the radial acceleration of a point on the
edge of the grinding wheel.
ANS. : 262 rad s1; 46 m s1, 1.2  104 m s2
40

41. DF025 CHAPTER 8
Exercise 8.1b&c :
3. A rotating wheel required 3.00 s to rotate through 37.0
revolution. Its angular speed at the end of the 3.00 s interval is
98.0 rad s-1. Calculate the constant angular acceleration of the
wheel.
ANS. : 13.6 rad s2
4. A wheel rotates with a constant angular acceleration of
3.50 rad s2.
a. If the angular speed of the wheel is 2.00 rad s1 at t =0,
through what angular displacement does the wheel rotate in
2.00 s.
b. Through how many revolutions has the wheel turned during
this time interval?
c. What is the angular speed of the wheel at t = 2.00 s?
ANS. : 11.0 rad; 1.75 rev; 9.00 rad s1
41

42. DF025 CHAPTER 8
Exercise 8.1b&c :
5. A bicycle wheel is being tested at a repair shop. The angular
velocity of the wheel is 4.00 rad s-1 at time t = 0 , and its angular
acceleration is constant and equal 1.20 rad s-2. A spoke OP on
the wheel coincides with the +x-axis at time t = 0 as shown in
Figure 7.8. y
P x
O
Figure 8.8
a. What is the wheel’s angular velocity at t = 3.00 s?
b. What angle in degree does the spoke OP make with the
positive x-axis at this time?
ANS. : 0.40 rad s1; 18
42

43. DF025 CHAPTER 8
Learning Outcome:
8.2 Equilibrium of a uniform rigid body
(2 hours)
At the end of this chapter, students should be able to:
a) Define and use torque, τ
b) State and use conditions for equilibrium of rigid body:

F x  0, F y  0,  τ 0
 Examples of problems :
Fireman ladder leaning on a wall, see-saw, pivoted /
suspended horizontal bar.
 Sign convention for moment or torque :
+ve : anticlockwise
43
ve : clockwise

44. DF025 CHAPTER 8
8.2 Equilibrium of a rigid body
Non-concurrent forces
 is defined as the forces whose lines of action do not pass
through a single common point.
 The forces cause the rotational motion on the body.
 The combination of concurrent and non-concurrent forces cause
rolling motion on the body. (translational and rotational
motion)
 Figure 5.11 shows an example of non-concurrent forces.
 
F1 F2

F4 
Figure 8.2 F3 44

45. DF025 CHAPTER 8

Torque (moment of a force), 
 The magnitude of the torque is defined as the product of a
force and its perpendicular distance from the line of action
of the force to the point (rotation axis).
τ  Fd
OR
where τ : magnitude of the torque
F : magnitude of the force
d : perpendicular distance (moment arm)
Because of d  r sin 
where r : distance between the pivot point (rotation
axis) and the point of application of force.
Thus
  
  Fr sin  OR   r F
 
where  : angle between F and r
45

46. DF025 CHAPTER 8
 It is a vector quantity.
 The dimension of torque is
   F d   ML T2 2
 The unit of torque is N m (newton metre), a vector product
unlike the joule (unit of work), also equal to a newton metre,
which is scalar product.
 Torque is occurred because of turning (twisting) effects of the
forces on a body.
 Sign convention of torque:
 Positive - turning tendency of the force is anticlockwise.
 Negative - turning tendency of the force is clockwise.
 The value of torque depends on the rotation axis and the
magnitude of applied force.
46

47. DF025 CHAPTER 8
Case 1 :
 Consider a force is applied to a metre rule which is pivoted at
one end as shown in Figures 5.12a and 5.12b.

F τ  Fd
(anticlockwise)
d
Figure 8.12a
Line of action of a force
Pivot point
(rotation axis) Point of action of a force

d  r sin θ F
θ
τ  Fd  Fr sin θ
r (anticlockwise)
Figure 8.12b 47

48. DF025 CHAPTER 8
Case 2 :
 Consider three forces are applied to the metre rule which is
pivoted at one end (point O) as shown in Figures 5.13.
τ1  F1d1  F1r1 sin θ1

F3 d1  r1 sin θ1 τ 2   F2 d 2   F2 r2 sin θ2

F1 τ 3  F3 d 3  F3 r3 sin θ3  0
r2 r1 θ1 Therefore the resultant (nett)
torque is
O
d 2  r2 sin θ2
θ2  τ O  τ1  τ 2  τ 3
τ
 F2 Figure 8.13
O  F1d1  F2 d 2
 Caution :
 If the line of action of a force is through the rotation axis
then
τ  Fr sin θ and θ 0 
τ 0 Simulation 8.2 48

49. DF025 CHAPTER 8
Example 4 :
Determine a resultant torque of all the forces about rotation axis, O
in the following problems.
a. F  10 N
2
5m 5m F1  30 N
3m
O 6m
3m
10 m
F3  20 N
49

50. DF025 CHAPTER 8
Example 4 :
b.
10 m F1  30 N
3m
6m
β O
3m
F3  20 N
5m 5m
α F4  25 N
F2  10 N
50

51. DF025 CHAPTER 8
Solution : F2  10 N
a. 5m 5m F1  30 N
d1  3 m
6m
O d2  5 m
10 m
Force Torque (N m), o=Fd=Frsin

F3  20 N F1  30 3  90

F2  10 5  50

The resultant torque: F3 0
τ O  90  50  40 N m
(clockwise) 51

52. DF025 CHAPTER 8
Solution :
b. 10 m F1  30 N
3m d3 d  3 m
β O
1
6m
β r 5m 3
sin β   0.515
F3  20 N 5m 5m
32  5 2
F2  10 N α F4  25 N
Force Torque (N m), o=Fd=Frsin

F1  30 3  90

F2 0 The resultant torque:

F3 F3 r sin β  2050.515   51.5 τ O  90  51.5

F4 0
τ O  38.5 N m
(clockwise)
52

53. DF025 CHAPTER 8
8.2 Equilibrium of a rigid body
 Rigid body is defined as a body with definite shape that
doesn’t change, so that the particles that compose it stay in
fixed position relative to one another even though a force is
exerted on it.
 If the rigid body is in equilibrium, means the body is
translational and rotational equilibrium.
 There are two conditions for the equilibrium of forces acting on
a rigid body.
 The vector sum of all forces acting on a rigid body must
be zero. 
F  F nett 0
OR
F x  0, Fy  0, F z 0
53

54. DF025 CHAPTER 8
 The vector sum of all external torques acting on a rigid
body must be zero about any rotation axis.

   τ nett  0
 This ensures rotational equilibrium.
 This is equivalent to the three independent scalar
equations along the direction of the coordinate axes,
τ x  0, τ y  0, τ z 0
Centre of gravity, CG
 is defined as the point at which the whole weight of a body
may be considered to act.
 A force that exerts on the centre of gravity of an object will
cause a translational motion.
54

55. DF025 CHAPTER 8
 Figures 5.14 and 5.15 show the centre of gravity for uniform
(symmetric) object i.e. rod and sphere
 rod – refer to the midway point between its end.
l
CG
l l
2 2
Figure 5.14
 sphere – refer to geometric centre.
CG
Figure 5.15
55

56. DF025 CHAPTER 8
5.3.4 Problem solving strategies for equilibrium of
a rigid body
 The following procedure is recommended when dealing with
problems involving the equilibrium of a rigid body:
 Sketch a simple diagram of the system to help
conceptualize the problem.
 Sketch a separate free body diagram for each body.
 Choose a convenient coordinate axes for each body and
construct a table to resolve the forces into their
components and to determine the torque by each force.
 Apply the condition for equilibrium of a rigid body :
F x  0; F
y 0 and
τ  0
 Solve the equations for the unknowns.
56

57. DF025 CHAPTER 8
Example 5 :
A 35 O 75 B
cm cm
W1
W2
Figure 5.16
A hanging flower basket having weight, W2 =23 N is hung out over
the edge of a balcony railing on a uniform horizontal beam AB of
length 110 cm that rests on the balcony railing. The basket is
counterbalanced by a body of weight, W1 as shown in Figure 5.16.
If the mass of the beam is 3.0 kg, calculate
a. the weight, W1 needed,
b. the force exerted on the beam at point O.
(Given g =9.81 m s2) 57

58. DF025 CHAPTER 8

Solution : m  3 kg; W2  23 N N
The free body diagram of the beam :
0.20 m
A 0.35 m 0.75 m B
CG
O
 
W2 0.55 m  0.55 m
W1
mg
Let point O as the rotation axis.
Force y-comp. (N) Torque (N m), o=Fd=Frsin

W1  W1  W1 0.75   0.75W1

W2  23  230.35   8.05
mg
  39.81  29.4 0.20   5.88
  29.4
N N 0
58

59. DF025 CHAPTER 8
Solution :
Since the beam remains at rest thus the system in equilibrium.
a. Hence
τ O 0
 0.75W1  8.05  5.88  0
W1  2.89 N
b. and F y 0
 W1  23  29.4  N  0
 2.89   23  29.4  N  0
N  55.3 N
59

60. DF025 CHAPTER 8
Example 6 :
A uniform ladder AB of length 10 m and
mass 5.0 kg leans against a smooth wall
as shown in Figure 5.17. The height of the A
end A of the ladder is 8.0 m from the
rough floor.
a. Determine the horizontal and vertical
forces the floor exerts on the end B of
the ladder when a firefighter of mass
60 kg is 3.0 m from B.
b. If the ladder is just on the verge of
slipping when the firefighter is 7.0 m smooth
wall B
up the ladder , Calculate the coefficient
of static friction between ladder and rough floor
floor. Figure 5.17
(Given g =9.81 m s2)
60

61. DF025 CHAPTER 8
Solution : ml  5.0 kg; m f  60 kg
a. The free body diagram of the ladder :
Let point B as the rotation axis. 
A N1
x-comp. y-comp. Torque (N m), 8
Force
(N) (N) B=Fd=Frsin α sin α   0.8
β 10

ml g 0  49.1 49.15.0sin β 6
sin β   0.6
 147 10

mf g 0  589
589 3.0 sin β 8.0 m CG 10 m
  1060 
N1 N1 0  N1 10sin α ml g β 3.0 m

 8 N 1  N2
 mf g β
N2 0 N2 0 5.0 m α
  B
fs  fs 0 0 fs
6.0 m
61

62. DF025 CHAPTER 8
Solution :
Since the ladder in equilibrium thus
τ B
0
147  1060  8N1  0
N1  151 N
F x
0
N1  f s  0
Horizontal force:f s  151 N
F y  0
 49.1  589  N 2  0
Vertical force: N 2  638 N
62

63. DF025 CHAPTER 8
Solution : sin α  0.8; sin β  0.6
b. The free body diagram of the ladder :

Let point B as the rotation axis. A N1
x-comp. y-comp. Torque (N m), α
Force
(N) (N) B=Fd=Frsin β

ml g 0  49.1 49.15.0sin β 
 147 mf g
β 10 m

mf g 0  589
589 7.0sin β 8.0 m

7.0 m
  2474 ml g β
N1 N1 0  N1 10sin α 
 8 N 1 N2
 5.0 m α
N2 0 N2 0  B
 fs
fs  μs N 2 0 0 6.0 m
63

64. DF025 CHAPTER 8
Solution :
Consider the ladder stills in equilibrium thus
τ B
0
147  2474  8N1  0
N1  328 N
 Fy 0
 49.1  589  N 2  0
N 2  638 N
F x  0
N 1  μs N 2  0
328  μs 638  0
μs  0.514
64

65. DF025 CHAPTER 8
Example 7 :
A floodlight of mass 20.0 kg in a park is
supported at the end of a 10.0 kg uniform
horizontal beam that is hinged to a pole as
shown in Figure 5.18. A cable at an angle
30 with the beam helps to support the light.
a. Sketch a free body diagram of the beam.
b. Determine
i. the tension in the cable,
ii. the force exerted on the beam by the
pole.
Figure 5.18
(Given g =9.81 m s2)
65

66. DF025 CHAPTER 8
Solution : m f  20.0 kg; mb  10.0 kg
a. The free body diagram of the beam :
 
S T
30 
O 0.5l CG 
mb g
l 
mf g
b. Let point O as the rotation axis.
Force x-comp. (N) y-comp. (N) Torque (N m), o=Fd=Frsin

mf g 0 196  196 l

mb g 0  98.1  98.10.5l   49.1l

T  T cos 30

T sin 30 
Tl sin 30  0.5Tl

S Sx Sy 0
66

67. DF025 CHAPTER 8
Solution :
b. The floodlight and beam remain at rest thus
i.
 τ 0
O
196l  49.1l  0.5Tl  0
T  490 N
ii. F x  0
 T cos 30   S x  0
S x  424 N
F y  0
 196  98.1  T sin 30  S y  0
S y  49.1 N
67

68. DF025 CHAPTER 8
Solution :
b. ii. Therefore the magnitude of the force is
S  Sx  S y
2 2
S 424 2  49.12
S  427 N
and its direction is given by
1 
Sy 
θ  tan  
S 
 x
1 
49.1 
θ  tan  
 424 
θ  6.61 from the +x-axis anticlockwise
68

69. DF025 CHAPTER 8
Exercise 8.2 :
Use gravitational acceleration, g = 9.81 m s2

1. F1
a B

A F2
b
D
C γ

Figure 8.19 F3
Figure 5.19 shows the forces, F1 =10 N, F2= 50 N and F3=
60 N are applied to a rectangle with side lengths, a = 4.0 cm
and b = 5.0 cm. The angle  is 30. Calculate the resultant
torque about point D.
ANS. : -3.7 N m 69

70. DF025 CHAPTER 8
Exercise 8.2 :
2.
Figure 5.20
A see-saw consists of a uniform board of mass 10 kg and length
3.50 m supports a father and daughter with masses 60 kg and
45 kg, respectively as shown in Figure 5.20. The fulcrum is
under the centre of gravity of the board. Determine
a. the magnitude of the force exerted by the fulcrum on the
board,
b. where the father should sit from the fulcrum to balance the
system.
ANS. : 1128 N; 1.31 m 70

71. DF025 CHAPTER 8
Exercise 8.2 :
3.
Figure 5.21
A traffic light hangs from a structure as show in Figure 5.21. The
uniform aluminum pole AB is 7.5 m long has a mass of 8.0 kg.
The mass of the traffic light is 12.0 kg. Determine
a. the tension in the horizontal massless cable CD,
b. the vertical and horizontal components of the force exerted
by the pivot A on the aluminum pole.
71
ANS. : 248 N; 197 N, 248 N

72. DF025 CHAPTER 8
Exercise 8.2 :
4.
30.0 cm 50.0 
15.0 cm

F
Figure 5.22
A uniform 10.0 N picture frame is supported by two light string
as shown in Figure 5.22. The horizontal force, F is applied for
holding the frame in the position shown.
a. Sketch the free body diagram of the picture frame.
b. Calculate
i. the tension in the ropes,
ii. the magnitude of the horizontal force, F .
ANS. : 1.42 N, 11.2 N; 7.20 N 72

73. DF025 CHAPTER 8
8.3 Rotational Dynamics (1 hour)
Centre of mass (CM)
 is defined as the point at which the whole mass of a body
may be considered to be concentrated.
 Its coordinate (xCM, yCM) is given the expression below:
 n   n 

 mi xi    mi yi 
 i 1   
xCM   n  ; yCM   i 1
n 
  mi 

 
 i 1
mi 


 i 1


th
where mi : mass of the i particle
xi : x coordinate of the i th particle
yi : y coordinate of the i th particle
73

74. DF025 CHAPTER 8
Example 9 :
Two masses, 2 kg and 4 kg are located on the x-axis at x =2 m and
x =5 m respectively. Determine the centre of mass of this system.
Solution : m1  2 kg; m2  4 kg m 2
m1
CM
x 0 2m 4m 5m
2
m x i i
m1 x1  m2 x2 22  45
xCM  i 1
 xCM 
2
m1  m2 2  4
m
i 1
i xCM  4 m from x  0
OR
2 m from m1
74

75. DF025 CHAPTER 8
Example 10 :
A system consists of three particles have the following masses and
coordinates :
(1) 2 kg, (1,1) ; (2) 4 kg, (2,0) and (3) 6 kg, (2,2).
Determine the coordinate of the centre of mass of the system.
Solution : m1  1 kg; m2  2 kg; m3  3 kg
The x coordinate of the CM is
3
m x
i 1
i i
m1 x1  m2 x2  m3 x3
xCM  
3
m1  m2  m3
m
i 1
i
xCM 
21  42  62 xCM  1.83
2  4  6
75

76. DF025 CHAPTER 8
Solution :
The y coordinate of the CM is
3
m y
i 1
i i
m1 y1  m2 y2  m3 y3
yCM  
3
m1  m2  m3
y
i 1
i
yCM 
21  40  62 yCM  1.17
2  4  6
Therefore the coordinate of the CM is
1.83,1.17 
76

77. DF025 CHAPTER 8
Moment of inertia, I
 Figure 7.9 shows a rigid body about a fixed axis O with angular
velocity .

m1
mn r1
rn r2 m2
Or m3
3
Figure 7.9
 is defined as the sum of the products of the mass of each
particle and the square of its respective distance from the
rotation axis.
77

78. DF025 CHAPTER 8
n
OR I m1r12
 m2 r22
 m3 r32
 ...mn rn2
 m r
i 1
i i
2
where I : moment of inertia of a rigid body about rotation axis
m : mass of particle
r : distance from the particle to the rotation axis
 It is a scalar quantity.
 Moment of inertia, I in the rotational kinematics is analogous
to the mass, m in linear kinematics.
 The dimension of the moment of inertia is M L2.
 The S.I. unit of moment of inertia is kg m2.
 The factors which affect the moment of inertia, I of a rigid body:
a. the mass of the body,
b. the shape of the body,
c. the position of the rotation axis.
78

79. DF025 CHAPTER 8
Moments of inertia of various bodies
 Table 7.3 shows the moments of inertia for a number of objects
about axes through the centre of mass.
Shape Diagram Equation
Hoop or ring or
thin cylindrical CM I CM  MR 2
shell
1
Solid cylinder or
disk
CM I CM  MR 2
2
79

80. DF025 CHAPTER 8
Moments of inertia of various bodies
 Table 7.3 shows the moments of inertia for a number of objects
about axes through the centre of mass.
Shape Diagram Equation
Uniform rod or
long thin rod with 1
rotation axis
CM
I CM  ML2
through the 12
centre of mass.
2
Solid Sphere CM I CM  MR 2
5
80

81. DF025 CHAPTER 8
Moments of inertia of various bodies
 Table 7.3 shows the moments of inertia for a number of objects
about axes through the centre of mass.
Shape Diagram Equation
Hollow Sphere or 2
thin spherical CM I CM  MR 2
shell 3
Table 7.3
81

82. DF025 CHAPTER 8
Example 11 :
Four spheres are arranged in a rectangular shape of sides 250 cm
and 120 cm as shown in Figure 7.10.
2 kg 3 kg
60 cm
A B
O
60 cm
5 kg 250 cm 4 kg
Figure 7.10
The spheres are connected by light rods . Determine the moment
of inertia of the system about an axis
a. through point O,
b. along the line AB.
82

83. DF025 CHAPTER 8
Solution : m1  2 kg; m2  3 kg; m3  4 kg; m4  5 kg
a. rotation axis about point O,
m1 m2
r1 r2 0.6 m
1.25 m
O
r4 r3
m4 m3
Since r1= r2= r3= r4= r thus r  0.6    1.25
2 2
 1.39 m
and the connecting rods are light therefore
I O  m1r12  m2 r22  m3r32  m4 r42
I O  r m1  m2  m3  m4   1.39  2  3  4  5
2 2
I O  27.0 kg m 2
83

84. DF025 CHAPTER 8
Solution : m1  2 kg; m2  3 kg; m3  4 kg; m4  5 kg
b. rotation axis along the line AB,
m1 m2
r1 r2
A B
r4 r3
m4 m3
r1= r2= r3= r4= r=0.6 m therefore
I AB  m1r12  m2 r22  m3r32  m4 r42
I AB  r m1  m2  m3  m4 
2
I AB  0.6 2  3  4  5
2
I AB  5.04 kg m 2
84

85. DF025 CHAPTER 8
Parallel-Axis Theorem (Steiner’s Theorem)
 States that the moment of inertia, I about any axis parallel to
and a distance, d away from the axis through the centre of
mass, ICM is given by
I  I CM  Md 2
where
I : moment of inertia about a new rotation axis
I CM : moment of inertia about an axis through CM
M : mass of the rigid body
d : distance between the new axis and the original axis
85

86. DF025 CHAPTER 8
Example 12 :
Determine the moment of inertia of a solid cylinder of radius R and
mass M about an axis tangent to its edge and parallel to its
symmetry axis as shown in Figure 7.11.
d
CM
Figure 7.11
Given the moment of inertia of the solid cylinder about axis through
the centre of mass is 1
I CM  MR 2
2 86

87. DF025 CHAPTER 8
Solution :
CM CM
1
I CM  MR 2 d
Initial 2 Final
From the diagram, d = R
By using the parallel axis theorem,
I  I CM  Md 2
1
I  MR 2  MR 2
2
3
I  MR 2
2
87

88. DF025 CHAPTER 8
Torque,
Relationship between torque, and angular acceleration, 
 Consider a force, F acts on a rigid body freely pivoted on an
axis through point O as shown in Figure 7.12.
a1 m1
mn

r1 F
an rn
O
r2 a2
m2
Figure 7.12
 The body rotates in the anticlockwise direction and a nett torque
is produced.
88

89. DF025 CHAPTER 8
 A particle of mass, m1 of distance r1 from the rotation axis O will
experience a nett force F1 . The nett force on this particle is
F1  m1a1 and a1  r1α
F1  m1r1α
 The torque on the mass m1 is
 1  r1F1 sin 90
 1  m1r1 
2
 The total (nett) torque on the rigid body is given by
  m1r12  m2 r22  ...  mn rn2
 n  n
  i 1 
    mi ri 2  and  mi ri 2  I
i 1
  I 89

90. DF025 CHAPTER 8
 From the equation, the nett torque acting on the rigid body is
proportional to the body’s angular acceleration.
 Note :
Nett torqu e ,   I
is analogous to the
Nett force,  F  ma
90

91. DF025 CHAPTER 8
Example 13 :
Forces, F1 = 5.60 N and F2 = 10.3 N are applied tangentially to a
disc with radius 30.0 cm and the mass 5.00 kg as shown in Figure
7.13.

F2
O
 30.0 cm
F1
Calculate, Figure 7.13
a. the nett torque on the disc.
b. the magnitude of angular acceleration influence by the disc.
1
( Use the moment of inertia, I CM  MR 2 )
2
91

92. DF025 CHAPTER 8
Solution : R  0.30 m; M  5.00 kg
a. The nett torque on the disc is
     1 2
  RF  RF 1  R F1  F2 
2
  0.30 5.60  10.3
  1.41 N m
b. By applying the relationship between torque and angular
acceleration,
1 2
  I    2 MR 
 
1 2
1.41   5.000.30 
2 
  6.27 rad s 2
92

93. DF025 CHAPTER 8
Example 14 :
A wheel of radius 0.20 m is mounted on a frictionless horizontal
axis. The moment of inertia of the wheel about the axis is
0.050 kg m2. A light string wrapped around the wheel is attached
to a 2.0 kg block that slides on a horizontal frictionless surface. A
horizontal force of magnitude P = 3.0 N is applied to the block as
shown in Figure 7.14. Assume the string does not slip on the
wheel.
Figure 7.14
a. Sketch a free body diagram of the wheel and the block.
b. Calculate the magnitude of the angular acceleration of the
wheel.
93

94. DF025 CHAPTER 8
Solution : R  0.20 m; I  0.050 kg m 2 ; P  3.0 N; m  2.0 kg
a. Free body diagram :
for wheel, 
 T
S

W 
 a
for block,
 N

T P

Wb
94

95. DF025 CHAPTER 8
Solution : R  0.20 m; I  0.050 kg m 2 ; P  3.0 N; m  2.0 kg
b. For wheel,
 τ  Iα Iα
RT  Iα T (1)
For block, R
 F  ma P  T  ma (2)
By substituting eq. (1) into eq. (2), thus
 Iα 
P     ma and a  Rα
R
 Iα 
P     mRα
R
 0.050α 
3.0     2.00.20 α α  4.62 rad s 2
 0.20 
95

96. DF025 CHAPTER 8
Example 15 :
An object of mass 1.50 kg is suspended
from a rough pulley of radius 20.0 cm by light
string as shown in Figure 7.15. The pulley
has a moment of inertia 0.020 kg m2 about
the axis of the pulley. The object is released
from rest and the pulley rotates without
encountering frictional force. Assume that R
the string does not slip on the pulley. After
0.3 s, determine
a. the linear acceleration of the object,
b. the angular acceleration of the pulley, 1.50 kg
c. the tension in the string, Figure 7.15
d. the liner velocity of the object,
e. the distance travelled by the object.
(Given g = 9.81 m s-2)
96

97. DF025 CHAPTER 8
Solution :
a. Free body diagram :
for pulley, 
S
 τ  Iα a
RT  Iα and α 
 a R
 RT  I  R 
 T  
W Ia
 T 2 (1)
for block,
T R
  F  ma
a mg  T  ma (2)

mg
97

98. DF025 CHAPTER 8
Solution : R  0.20 m; I  0.020 kg m 2 ; m  1.50 kg;
u  0; t  0.3 s
a. By substituting eq. (1) into eq. (2), thus
 Ia 
mg   2   ma
R 
 0.020 a 
1.50 9.81     1.50 a
 0.20 2  a  7.36 m s 2
 
b. By using the relationship between a and , hence
a  Rα
7.36  0.20α
α  36.8 rad s 2
98

99. DF025 CHAPTER 8
Solution : R  0.20 m; I  0.020 kg m 2 ; m  1.50 kg;
u  0; t  0.3 s
c. From eq. (1), thus
Ia
T 2 T
0.020 7.36 
R 0.20 2
T  3.68 N
d. By applying the equation of liner motion, thus
v  u  at
v  0  7.36 0.3 v  2.21 m s 1
(downwards)
e. The distance travelled by the object in 0.3 s is
1 2
s  ut  at
2
s  0  7.36 0.3
1
s  0.331 m
2
2
99

100. DF025 CHAPTER 8
Exercise 8.3 :
Use gravitational acceleration, g = 9.81 m s2
1. Three odd-shaped blocks of chocolate have following masses
and centre of mass coordinates: 0.300 kg, (0.200 m,0.300 m);
0.400 kg, (0.100 m. -0.400 m); 0.200 kg, (-0.300 m, 0.600 m).
Determine the coordinates of the centre of mass of the system
of three chocolate blocks.
ANS. : (0.044 m, 0.056 m)
2. Figure 7.16 shows four masses that are held at 70 g
the corners of a square by a very light 40 cm
frame. Calculate the moment of inertia 80 cm
of the system about an axis perpendicular B
to the plane 150 g A 150 g
a. through point A, and 80 cm
b. through point B.
Figure 7.16 70 g
ANS. : 0.141 kg m2; 0.211 kg m2 100

101. DF025 CHAPTER 8
Exercise 8.3 :
3. A 5.00 kg object placed on a
frictionless horizontal table is
connected to a string that passes 2.00 m s 2
over a pulley and then is fastened
to a hanging 9.00 kg object as in T1
Figure 7.17. The pulley has a
radius of 0.250 m and moment of
inertia I. The block on the table is T2
moving with a constant
acceleration of 2.00 m s2.
a. Sketch free body diagrams of
both objects and pulley.
b. Calculate T1 and T2 the tensions Figure 7.17
in the string.
c. Determine I.
ANS. : 10.0 N, 70.3 N; 1.88 kg m2 101

102. DF025 CHAPTER 8
Learning Outcome:
8.4 Work and Energy of Rotational Motion(2 hours)
At the end of this chapter, students should be able to:
a) Solve problems related to:
 Rotational kinetic energy,
1 2
K r  Iω
2
 work,
W  τθ
 power,
P  τω
102

103. DF025 CHAPTER 8
Rotational kinetic energy and power
Rotational kinetic energy, Kr
 Consider a rigid body rotating about the axis OZ as shown in
Figure 7.18.
Z
v1 m1
mn r1
vn rn r2 v2
O m2
r3 v3
m3
Figure 7.18
 Every particle in the body is in the circular motion about point O.
103

104. DF025 CHAPTER 8
 The rigid body has a rotational kinetic energy which is the total
of kinetic energy of all the particles in the body is given by
1 1 1 1
K r  m1v1  m2 v2  m3v3  ...  mn vn
2 2 2 2
2 2 2 2
1 1 1 1
K r  m1r1 ω  m2 r2 ω  m3 r3 ω  ...  mn rn2 ω2
2 2 2 2 2 2
2 2 2 2
1 2

K r  ω m1r12  m2 r22  m3 r32  ...  mn rn2
2

1 2 n   n 2

K r  ω  mi ri  and   mi ri   I
2
 
2  i 1


  i 1 
1 2
K r  Iω
2
104

105. DF025 CHAPTER 8
 From the formula for translational kinetic energy, Ktr
1 2
K tr  mv
2
 After comparing both equations thus
 is analogous to v
I is analogous to m
 For rolling body without slipping, the total kinetic energy of
the body, K is given by
K  K tr  K r
where K tr : translati onal kinetic energy
K r : rotational kinetic energy
105

106. DF025 CHAPTER 8
Example 16 :
A solid sphere of radius 15.0 cm and mass 10.0 kg rolls down an
inclined plane make an angle 25 to the horizontal. If the sphere
rolls without slipping from rest to the distance of 75.0 cm and the
inclined surface is smooth, calculate
a. the total kinetic energy of the sphere,
b. the linear speed of the sphere,
c. the angular speed about the centre of mass.
2
(Given the moment of inertia of solid sphere is I CM  mR 2and
the gravitational acceleration, g = 9.81 m s2) 5
106

107. DF025 CHAPTER 8
Solution : R  0.15 m; m  10.0 kg
s  0.75 m R
h  s sin 25
v CM 25 
a. From the principle of conservation of energy,
E  E
i f
mgh  K
K  mgs sin 25
K  10.0 9.810.75sin 25 
K  31.1 J
107

108. DF025 CHAPTER 8
Solution : R  0.15 m; m  10.0 kg
b. The linear speed of the sphere is given by
K  K tr  K r 1 2 1 2 v
K  mv  Iω and ω 
2 2 R
2
1 2 12 2  v 
K  mv   mR  
2 25  R 
7
K  mv 2
10
31.1  10.0 v 2
7
v  2.11 m s 1
10
c. By using the relationship between v and , thus
v  Rω 2.11  0.15ω
ω  14.1 rad s 1
108

109. DF025 CHAPTER 8
Example 17 :
The pulley in the Figure 7.19 has a
radius of 0.120 m and a moment of
inertia 0.055 g cm2. The rope does not
slip on the pulley rim.
Calculate the speed of the 5.00 kg
block just before it strikes the floor.
(Given g = 9.81 m s2) 5.00 kg
7.00 m
2.00 kg
Figure 7.19
109

110. DF025 CHAPTER 8
Solution : m1  5.00 kg; m2  2.00 kg; R  0.120 m; h  7.00 m
The moment of inertia of the pulley,
 10 3 kg  10 4 m 2 
 
I  0.055 g  1 cm2  
 1 g  1 cm2 
  5.5  10 9 kg m 2
  
m1 m2 v
7.00 m 7.00 m
m2 v m1
Initial Final
E i  U1 E f Ktr1  Ktr 2  K r  U 2
110

111. DF025 CHAPTER 8
Solution : m1  5.00 kg; m2  2.00 kg; R  0.120 m;
h  7.00 m; I  5.5 10 9 kg m 2
By using the principle of conservation of energy, thus
E  Ei f
U 1  K tr1  K tr 2  K r  U 2
1 1 1 2
m1 gh  m1v  m2v  Iω  m2 gh
2 2
2 2 2 2
1 v
m1  m2 gh  v m1  m2   I  
1 2
2 2 R
 
2
 v 
5.00  2.00 9.817.00   v 5.00  2.00   5.5 10 9
1 2 1
 
2 2  0.120 
v  7.67 m s 1
111

112. DF025 CHAPTER 8
Work, W
 Consider a tangential force, F acts on the solid disc of radius R
freely pivoted on an axis through O as shown in Figure 7.20.
ds
d
R 
R F
O
Figure 7.20
 The work done by the tangential force is given by
dW  Fds and ds  Rdθ
dW  FRdθ
θ2 θ2
 dW   θ1
τdθ W θ1
τdθ
112

113. DF025 CHAPTER 8
 If the torque is constant thus
2
W    d
1
W    2  1 
W   is analogous to the W  Fs
where τ : torque
Δθ : change in angular displacement
W : work done
 Work-rotational kinetic energy theorem states
W  K r  K r  f  K r i
1 2 1 2
W  Iω  Iω0
2 2
113

114. DF025 CHAPTER 8
Power, P
 From the definition of instantaneous power,
dW
P and dW  τdθ
dt
τdθ and dθ
P ω
dt dt
P  τω is analogous to the P  Fv
 Caution :
 The unit of kinetic energy, work and power in the
rotational kinematics is same as their unit in translational
kinematics.
114

115. DF025 CHAPTER 8
Example 18 :
A horizontal merry-go-round has a radius of 2.40 m and a
moment of inertia 2100 kg m2 about a vertical axle through its
centre. A tangential force of magnitude 18.0 N is applied to the
edge of the merry-go- round for 15.0 s. If the merry-go-round is
initially at rest and ignore the frictional torque, determine
a. the rotational kinetic energy of the merry-go-round,
b. the work done by the force on the merry-go-round,
c. the average power supplied by the force.
(Given g = 9.81 m s2)
Solution :

R  2.40 m F
115

116. DF025 CHAPTER 8
Solution : R  2.40 m; I  2100 kg m 2 ; F  18.0 N;
t  15.0 s; ω0  0
a. By applying the relationship between nett torque and angular
acceleration, thus
 τ  Iα
RF  Iα 2.4018.0   2100 α
α  2.06  10 2 rad s 2
Use the equation of rotational motion with uniform angular
acceleration, ω  ω0  αt

ω  0  2.06 10 15.0
2

ω  0.309 rad s 1
Therefore the rotational kinetic energy for 15.0 s is
1 2
K r  2100 0.309 
1
K r  Iω 2
2 2
K r  100 J
116

117. DF025 CHAPTER 8
Solution : R  2.40 m; I  2100 kg m 2 ; F  18.0 N;
t  15.0 s; ω0  0
b. The angular displacement,  for 15.0 s is given by
1 2
θ  ω0t  αt
2
1
2

θ  0  2.06  10 2 15.0 
2
θ  2.32 rad
By applying the formulae of work done in rotational motion, thus
W  τθ W  RFθ
W  2.40 18.0 2.32 
W  100 J
c. The average power supplied by the force is
W 100
Pav  Pav 
t 15.0
Pav  6.67 W
117

118. DF025 CHAPTER 8
Learning Outcome:
8.5 Conservation of angular momentum (1 hour)
At the end of this chapter, students should be able to:
 Define and use the formulae of angular momentum,
L  Iω
 State and use the principle of conservation of angular
momentum
118

119. DF025 CHAPTER 8
Conservation of angular momentum

Angular momentum, L
 is defined as the product of the angular velocity of a body
and its moment of inertia about the rotation axis.
L  I
OR
is analogous to the p  mv
where L : angular momentum
I : moment of inertia of a body
ω : angular velocity of a body
 It is a vector quantity.
 Its dimension is M L2 T1
 The S.I. unit of the angular momentum is kg m2 s1.
119

120. DF025 CHAPTER 8
 The relationship between angular momentum, L with linear
momentum, p is given by    
vector notation : L  r  p  r  mv
magnitude form :
L  rp sin θ  mvr sin θ
where
r : distance from the particle to the rotation axis

θ : the angle between r with v
 Newton’s second law of motion in term of linear momentum is

 

dp
F  Fnett 
dt
hence we can write the Newton’s second law in angular form as

 

dL
τ  τ nett 
dt
and states that the vector sum of all the torques acting on a
rigid body is proportional to the rate of change of angular
momentum. 120

121. DF025 CHAPTER 8
Principle of conservation of angular momentum
 states that the total angular momentum of a system about an
rotation axis is constant if no external torque acts on the
system.
OR

I  constant If the
 τ 0
Therefore 
 dL
 τ
 dt
0
dL  0 and dL   L f - Li
 
 Li   L f
121

122. DF025 CHAPTER 8
Example 19 :
A 200 kg wooden disc of radius 3.00 m is rotating with angular
speed 4.0 rad s-1 about the rotation axis as shown in Figure
7.21. A 50 kg bag of sand falls onto the disc at the edge of the
wooden disc.
ω0 
R R
Before Figure 7.21 After
Calculate,
a. the angular speed of the system after the bag of sand falling
onto the disc. (treat the bag of sand as a particle)
b. the initial and final rotational kinetic energy of the system.
Why the rotational kinetic energy is not the same?
1
(Use the moment of inertia of disc is MR2 )
2 122

123. DF025 CHAPTER 8
Solution : R  3.00 m; ω0  4.0 rad s 1 ; mw  200 kg; mb  50 kg
a. The moment of inertia of the disc,
I w  mw R  200 3.00 
1 2 1 2
2 2
I w  900 kg m 2
The moment of inertia of the bag of sand,
I b  mb R 2  50 3.00 
2
I b  450 kg m 2
 
By applying the principle of conservation of angular momentum,
L  L
i f
I wω0  I w  I b ω
900 4.0  900  450 ω
ω  2.67 rad s 1
123

124. DF025 CHAPTER 8
Solution : R  3.00 m; ω0  4.0 rad s 1 ; mw  200 kg; mb  50 kg
b. The initial rotational kinetic energy,
K r i  I wω0  900 4.0
1 2 1 2
2 2
K r i  7200 J
The final rotational kinetic energy,
K r  f  I w  I b ω  900  450 2.67 
1 2 1 2
2 2
K r  f  4812 J
   
thus K r i  K r f
It is because the energy is lost in the form of heat from the
friction between the surface of the disc with the bag of
sand.
124

125. DF025 CHAPTER 8
Example 20 :
A raw egg and a hard-boiled egg are rotating about the same
axis of rotation with the same initial angular velocity. Explain
which egg will rotate longer.
Solution :
The answer is hard-boiled egg.
125

126. DF025 CHAPTER 8
Solution :
Reason
Raw egg :
When the egg spins, its yolk being denser moves away from the
axis of rotation and then the moment of inertia of the egg increases
because of I  mr 2
From the principle of conservation of angular momentum,
I  constant
If the I is increases hence its angular velocity,  will decreases.
Hard-boiled egg :
The position of the yolk of a hard-boiled egg is fixed. When the egg
is rotated, its moment of inertia does not increase and then its
angular velocity is constant. Therefore the egg continues to spin.
126

127. DF025 CHAPTER 8
Example 21 :
A student sits on a freely rotating stool holding two weights, each
of mass 3.00 kg as shown in Figure 7.22.
When his arms are extended horizontally, the weights are 1.00 m
from the axis of rotation and he rotates with an angular speed of
0.750 rad s1. The moment of inertia of the student and stool is
3.00 kg m2 and is assumed to be constant. The student pulls the
weights inward horizontally to a position 0.300 m from the
rotation axis. Determine
 
a. the new angular speed of the student. 0
b. the kinetic energy of the rotating
system before and after he pulls
the weights inward.
Before After
Figure 7.22
127

128. DF025 CHAPTER 8
Solution : mw  3.00 kg; ω0  0.750 rad s 1; I ss  3.00 kg m 2
0 
rb rb
mw mw
ra ra
Before After
128

129. DF025 CHAPTER 8
Solution : mw  3.00 kg; ω0  0.750 rad s 1; I ss  3.00 kg m 2 ;
rb  1.00 m; ra  0.300 m
a. The moment of inertia of the system initially is
I i  I ss  I w 
I i  I ss  mw rb  mw rb
2 2

I i  I ss  2mw rb
2
Ii  3.00  23.001.002  9.00 kg m2
The moment of inertia of the system finally is
I f  I ss  2mw ra
2
I f  3.00  23.000.300   3.54 kg m2
2
 
By using the principle of conservation of angular momentum,
thus
 L  L
i  f
I i ω0  I f ω
9.00 0.750   3.54 ω
1
ω  1.91 rad s
129

130. DF025 CHAPTER 8
Solution : mw  3.00 kg; ω0  0.750 rad s 1; I ss  3.00 kg m 2 ;
rb  1.00 m; ra  0.300 m
b. The initial rotational kinetic energy is given by
K r i 1
 I i ω0
2
2
K r i  9.00 0.750 
1 2
2
K r i  2.53 J
and the final rotational kinetic energy is
K r  f 1
 I f ω2
2
K r  f  3.54 1.91
1 2
2
K r  f  6.46 J
130

131. DF025 CHAPTER 8
Exercise 8.5 :
Use gravitational acceleration, g = 9.81 m s2
1. A woman of mass 60 kg stands at the rim of a horizontal
turntable having a moment of inertia of 500 kg m2 and a radius
of 2.00 m. The turntable is initially at rest and is free to rotate
about the frictionless vertical axle through its centre. The
woman then starts walking around the rim clockwise (as viewed
from above the system) at a constant speed of 1.50 m s1
relative to the Earth.
a. In the what direction and with what value of angular speed
does the turntable rotate?
b. How much work does the woman do to set herself and the
turntable into motion?
ANS. : 0.360 rad s1 ,U think; 99.9 J
131

132. DF025 CHAPTER 8
Exercise 8.5 :
2. Determine the angular momentum of the Earth
a. about its rotation axis (assume the Earth is a uniform solid
sphere), and
b. about its orbit around the Sun (treat the Earth as a particle
orbiting the Sun).
Given the Earth’s mass = 6.0 x 1024 kg, radius = 6.4 x 106 m
and is 1.5 x 108 km from the Sun.
ANS. : 7.1 x 1033 kg m2 s1; 2.7 x 1040 kg m2 s1
3. Calculate the magnitude of the angular momentum of the
second hand on a clock about an axis through the centre of the
clock face. The clock hand has a length of 15.0 cm and a mass
of 6.00 g. Take the second hand to be a thin rod rotating with
angular velocity about one end. (Given the moment of inertia of
thin rod about the axis through the CM is 1 ML2 )
ANS. : 4.71 x 106 kg m2 s1 12
132

133. DF025 CHAPTER 8
Summary:
Linear Motion Relationship Rotational Motion
d
v
ds v  r 
dt dt
dv d
a a  r 
dt dt
n
m I   mi ri 2 I
i 1
 F  ma   rF sin    I
p  mv L  rp sin  L  I
W  Fs W  
P  Fv P  
133

134. DF015 CHAPTER 8
THE END…
Next Chapter…
CHAPTER 9 :
Simple Harmonic Motion
134