1. 機械学習入門 – SVMによる画像分類
yokkuns: 里 洋平
第３回 データマイニング+WEB 勉強会

2. 機械学習入門 – SVMによる画像分類
yokkuns: 里 洋平
第３回 データマイニング+WEB 勉強会

3. AGENDA
 自己紹介
 機械学習
 SVM
 マージンの最大化
 カーネル関数を用いた柔軟なモデリング
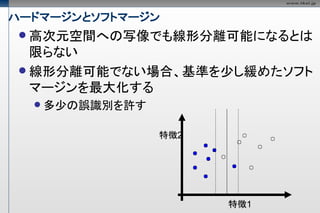
 ハードマージンとソフトマージン
 ラグランジュ乗数
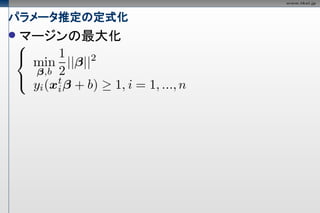
 パラメータ推定の定式化
 RによるSVMの使用例

4. 自己紹介
 id : yokkuns
 名前 : 里 洋平
 職業 : Webエンジニア
 出身 : 種子島
 趣味 : プログラミングとかカラオケとか
 主催してる勉強会 : Tokyo.R、数式ニヤニヤ勉強会
統計とか機械学習やりはじめたのは割と最近なので
、
突っ込み大歓迎です！

5. 機械学習とは

6. 機械学習とは
 人間が自然に行っている学習能力と同じ機能をコン
ピュータで実現させる技術・手法
 サンプルデータを対象に解析を行い、そのデータか
ら有用な規則、ルールなどを抽出
 大きく以下のように分類出来る
 教師あり学習
 教師なし学習
 強化学習

7. 記憶ベース推論
車

8. 記憶ベース推論
テレビ

9. 記憶ベース推論
ギター

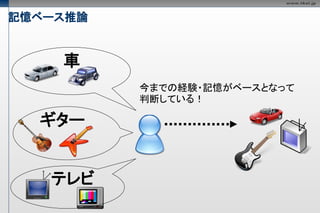
10. 記憶ベース推論
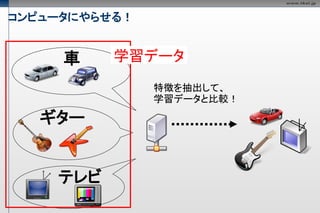
車
今までの経験・記憶がベースとなって
判断している！
ギター
テレビ

11. コンピュータにやらせる！
車 学習データ
特徴を抽出して、
学習データと比較！
ギター
テレビ

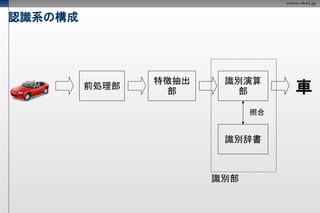
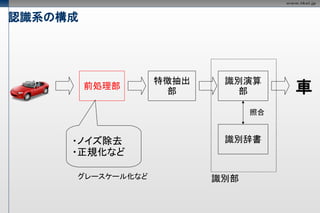
12. 認識系の構成
特徴抽出 識別演算
前処理部
部 部 車
照合
識別辞書
識別部

13. 認識系の構成
特徴抽出 識別演算
前処理部
部 部 車
照合
・ノイズ除去 識別辞書
・正規化など
グレースケール化など 識別部

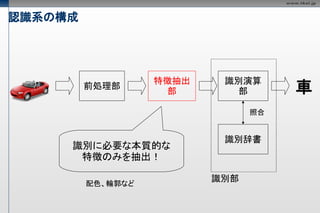
14. 認識系の構成
特徴抽出 識別演算
前処理部
部 部 車
照合
識別辞書
識別に必要な本質的な
特徴のみを抽出！
配色、輪郭など
識別部

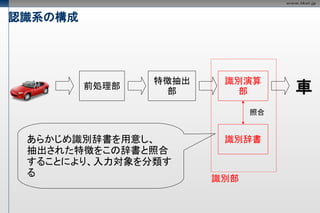
15. 認識系の構成
特徴抽出 識別演算
前処理部
部 部 車
照合
あらかじめ識別辞書を用意し、 識別辞書
抽出された特徴をこの辞書と照合
することにより、入力対象を分類す
る
識別部

16. サポートベクターマシン（SVM）

17. サポートベクターマシン
 実データの解析に広く利用されている判別手法
 特徴
 マージン最大化を基準とすることで、高い判別性能を実
現
 カーネル関数を用いた柔軟なモデリング
 パラメータ推定が凸2次最適化問題として定式化されるた
め、高速な最適化アルゴリズムが利用可能

18. サポートベクターマシン
 実データの解析に広く利用されている判別手法
 特徴
 マージン最大化を基準とすることで、高い判別性能を実
現
 カーネル関数を用いた柔軟なモデリング
 パラメータ推定が凸2次最適化問題として定式化されるた
め、高速な最適化アルゴリズムが利用可能

19. マージン最大化

20. マージン最適化

21. マージン最大化

22. マージン最大化

23. マージン最大化

24. マージン最大化

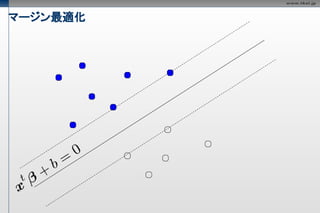
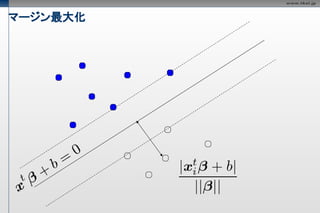
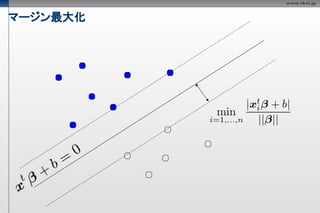
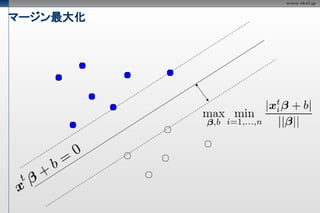
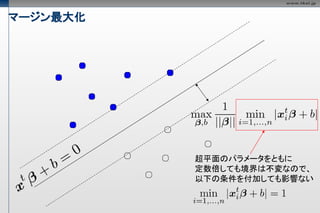
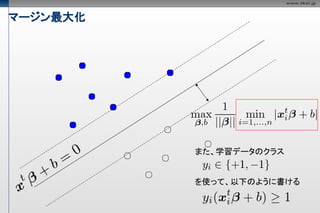
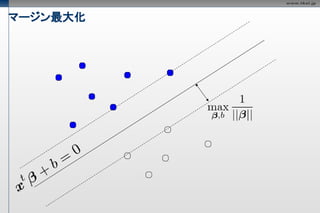
25. マージン最大化
超平面のパラメータをともに
定数倍しても境界は不変なので、
以下の条件を付加しても影響ない

26. マージン最大化
また、学習データのクラス
を使って、以下のように書ける

27. マージン最大化

28. マージン最大化
 よって、以下のように定式化出来る
 を解きやすい に置き換えている

29. サポートベクターマシン
 実データの解析に広く利用されている判別手法
 特徴
 マージン最大化を基準とすることで、高い判別性能を実
現
 カーネル関数を用いた柔軟なモデリング
 パラメータ推定が凸2次最適化問題として定式化されるた
め、高速な最適化アルゴリズムが利用可能

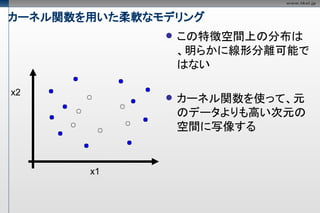
30. カーネル関数を用いた柔軟なモデリング
 この特徴空間上の分布は
、明らかに線形分離可能で
はない
x2
 カーネル関数を使って、元
のデータよりも高い次元の
空間に写像する
x1

31. 非線形変換
 データを高次元の空間へ写す
 内積は

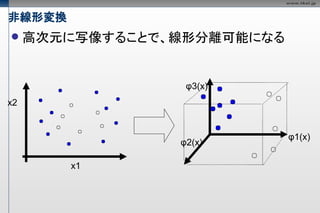
32. 非線形変換
 高次元に写像することで、線形分離可能になる
φ3(x)
x2
φ1(x)
φ2(x)
x1

33. ハードマージンとソフトマージン
 今までの前提
 線形分離可能
 出来ない場合でも、高次元空間への写像を使うことで線
形分離可能
 このように、学習線形分離可能をという条件のマー
ジンをハードマージンという

34. ハードマージンとソフトマージン
 高次元空間への写像でも線形分離可能になるとは
限らない
 線形分離可能でない場合、基準を少し緩めたソフト
マージンを最大化する
 多少の誤識別を許す
特徴2
特徴1

35. サポートベクターマシン
 実データの解析に広く利用されている判別手法
 特徴
 マージン最大化を基準とすることで、高い判別性能を実
現
 カーネル関数を用いた柔軟なモデリング
 パラメータ推定が凸2次最適化問題として定式化されるた
め、高速な最適化アルゴリズムが利用可能

36. パラメータ推定
 マージン最大化の学習過程は、ラグランジュ関数を
用いることで、凸2次計画問題になる
 サンプル数が増えると急激に計算量がふえるため、
分割統治法の考え方を用いた手法が提案されてい
る

37. パラメータ推定
 マージン最大化の学習過程は、ラグランジュ関数を
用いることで、凸2次計画問題になる
 サンプル数が増えると急激に計算量がふえるため、
分割統治法の考え方を用いた手法が提案されてい
る

38. 関数をベクトルで考える
 1次関数
は、 平面上で、各点 に高さ を
与えると、 空間中の平面を表す

39. 勾配
 x軸に平行な方向に1だけ進むと関数値は、aだけ増
え、 y軸に平行な方向に距離1だけ進むと
関数値はbだけ増える
 x軸、y軸方向への勾配の大きさがそれぞれ、a,b。これらを成
分とするベクトルを勾配と呼ぶ
 勾配は、関数値がもっとも急激に増大する方向を表す

40. 関数の等高線と勾配
 xy平面上で関数値が一定の軌跡を等高線と呼ぶ。
 点(x, y)での関数値をcとすると、点(x, y)は等高線
上にある。
 の勾配は、等高線 と直交す
る
 勾配は、関数値がもっとも増大する方向
 等高線がもっとも増大する方向は垂直方向
 等高線 の法線ベクトルは勾配

41. n変数関数への拡張
 以上のことは、n変数関数でも成り立つ
 n変数関数の勾配は、次のように定義される
 n変数関数 の勾配 は、
等値面 の法線ベクトルである

42. ラグランジュの未定乗数法
 制約条件が1つの場合
制約条件 のもとで関数 が極値を
とる点は
と置くと、次の式を満たす

43. ラグランジュの未定乗数法
 制約条件が1つの場合
制約条件 のもとで関数 が極値を
とる点は
と置くと、次の式を満たす
ラグランジュ乗数

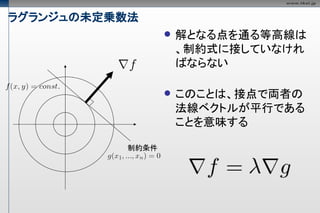
44. ラグランジュの未定乗数法
 解となる点を通る等高線は
、制約式に接していなけれ
ばならない
 このことは、接点で両者の
法線ベクトルが平行である
ことを意味する
制約条件

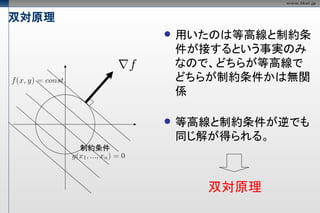
45. 双対原理
 用いたのは等高線と制約条
件が接するという事実のみ
なので、どちらが等高線で
どちらが制約条件かは無関
係
 等高線と制約条件が逆でも
同じ解が得られる。
制約条件
双対原理

46. ラグランジュ未定乗数法
 制約条件が複数の場合
制約条件 のもとで関数 が極値を
とる点は
と置くと、次の式を満たす

47. 線形計画と非線形計画
 線形計画
 線形制約条件のもとで線形関数を最大、最小にする
問題
 シンプレックス法とか使える
 非線形計画
 非線形制約条件のもとで非線形関数を最大、最小に
する問題
 一般的な理論も解法も存在しない
 制約条件や目的関数のもつ性質ごとに種々の定理が成立
し、さまざまな解法が存在する

48. 線形計画と非線形計画
 線形計画
 線形制約条件のもとで線形関数を最大、最小にする
問題
 シンプレックス法とか使える
 非線形計画
 非線形制約条件のもとで非線形関数を最大、最小に
する問題
 一般的な理論も解法も存在しない
 制約条件や目的関数のもつ性質ごとに種々の定理が成立
し、さまざまな解法が存在する

49. 非線形計画とラグランジュ乗数
 問題A
 は上に凸、 は全て下に凸、 は全て1
次式とする

50. 非線形計画とラグランジュ乗数
 このとき、以下のような関数を考える
 上の式を、問題Aのラグランジュ関数と呼ぶ
 また、このとき、KKT条件が成り立つ
 問題Aの解が存在する必要十分条件は、次の条件が成
り立つような が存在すること

51. 双対問題
 ラグランジュ関数Lにおいて、ラグランジュ乗数
{λi}、{μi}を定数とみなしてxに関して最大化した値
は{λi}、{μi}の関数である。これを
と置くと、次の問題を問題Aの双対問題と呼ぶ
 問題B

52. パラメータ推定の定式化
 マージンの最大化

53. パラメータ推定の定式化
 ラグランジュ乗数αを導入すると、ラグランジュ関数は、

54. パラメータ推定の定式化

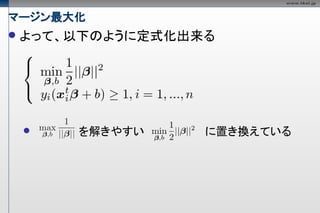
55. パラメータ推定の定式化
 よって、相対形式として、以下の凸2次計画問題を解
けばよい
 これを解く手法として、SMOなどがある

56. RによるSVMの使用例

57. スパムメールの学習と判別
4601 の電子メールを58 項目に分けて記録したもの
第58 列がクラス情報spam，nonspam で、残りの57 項目はメールの特徴

58. ご清聴ありがとうございました。

59. 参考文献
 わかりやすいパターン認識
 データマイニング手法―
営業、マーケティング、カスタマーサポートのための顧客分析
 Rによるデータサイエンス - データ解析の基礎から最新手法まで
 パターン認識 (Rで学ぶデータサイエンス 5)
 マシンラーニング (Rで学ぶデータサイエンス 6)
 これなら分かる最適化数学―基礎原理から計算手法まで