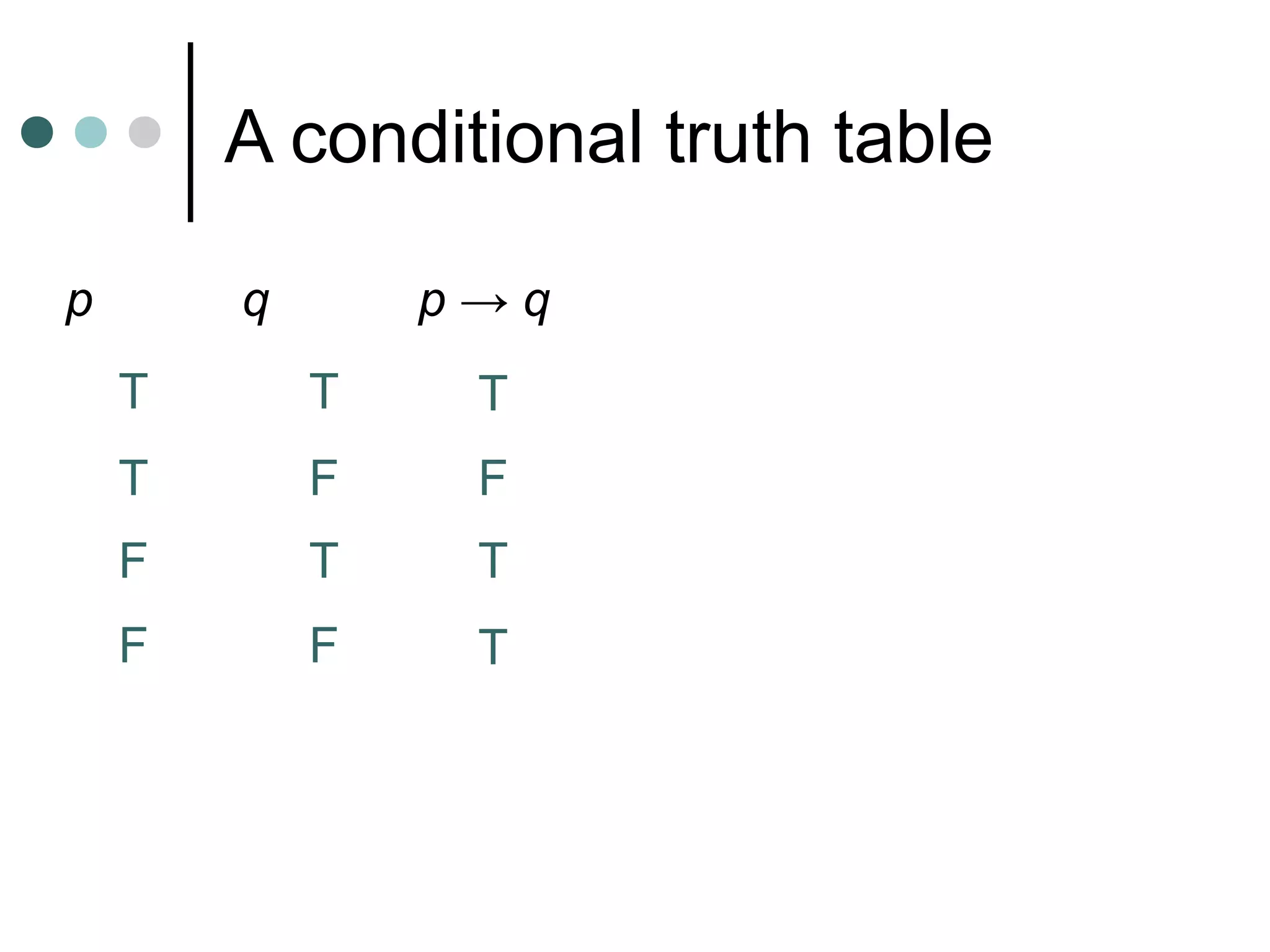
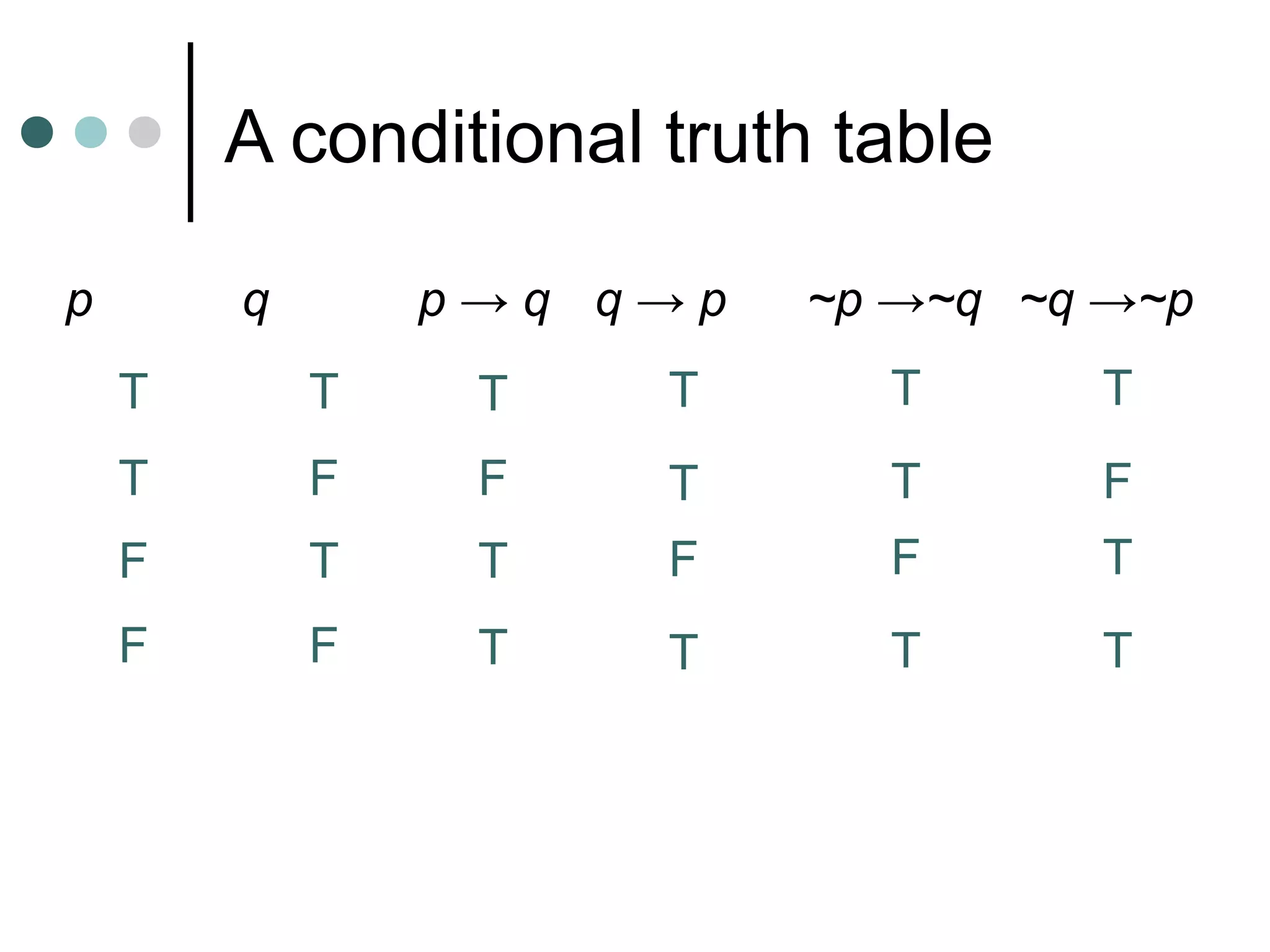
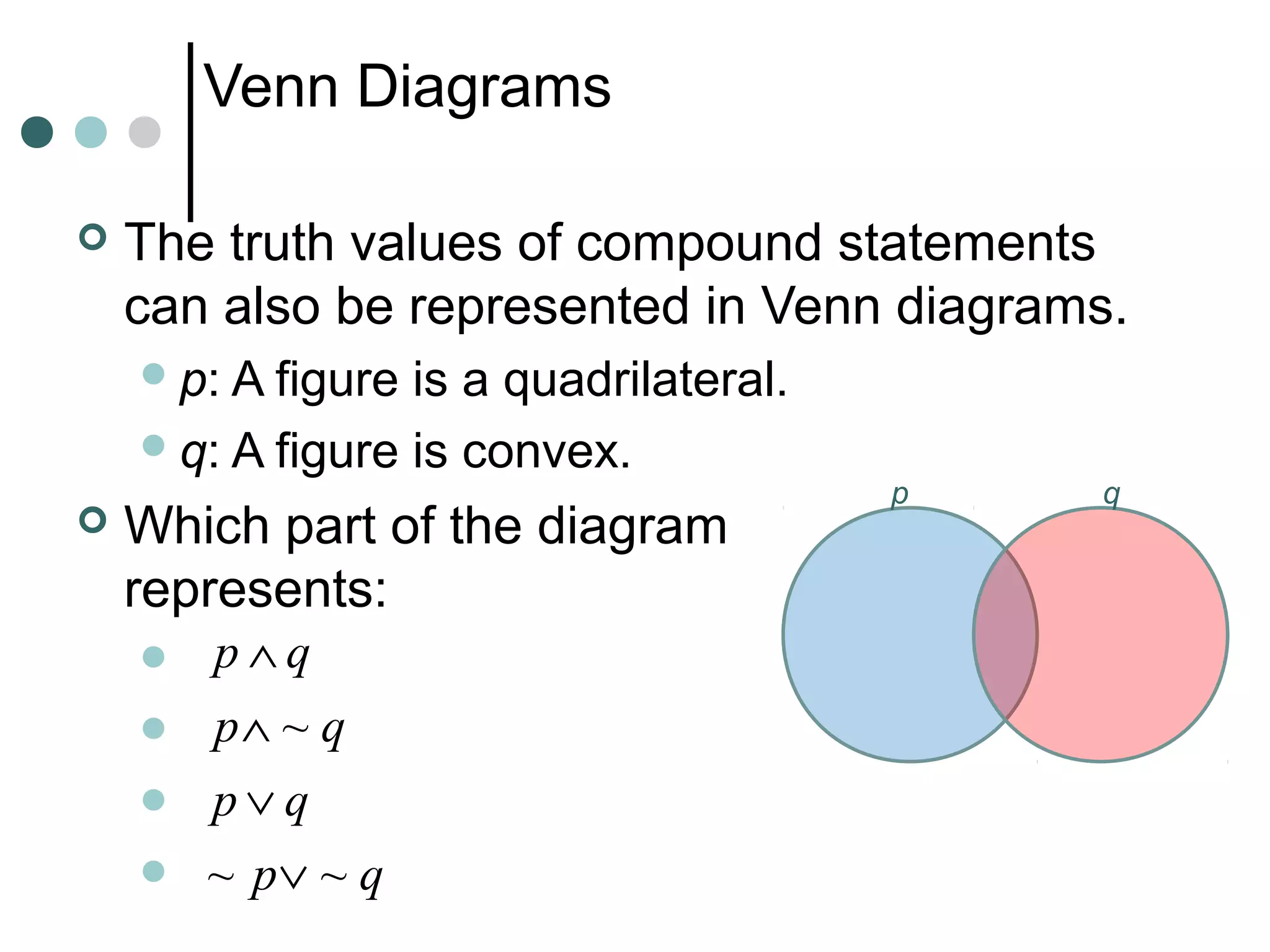
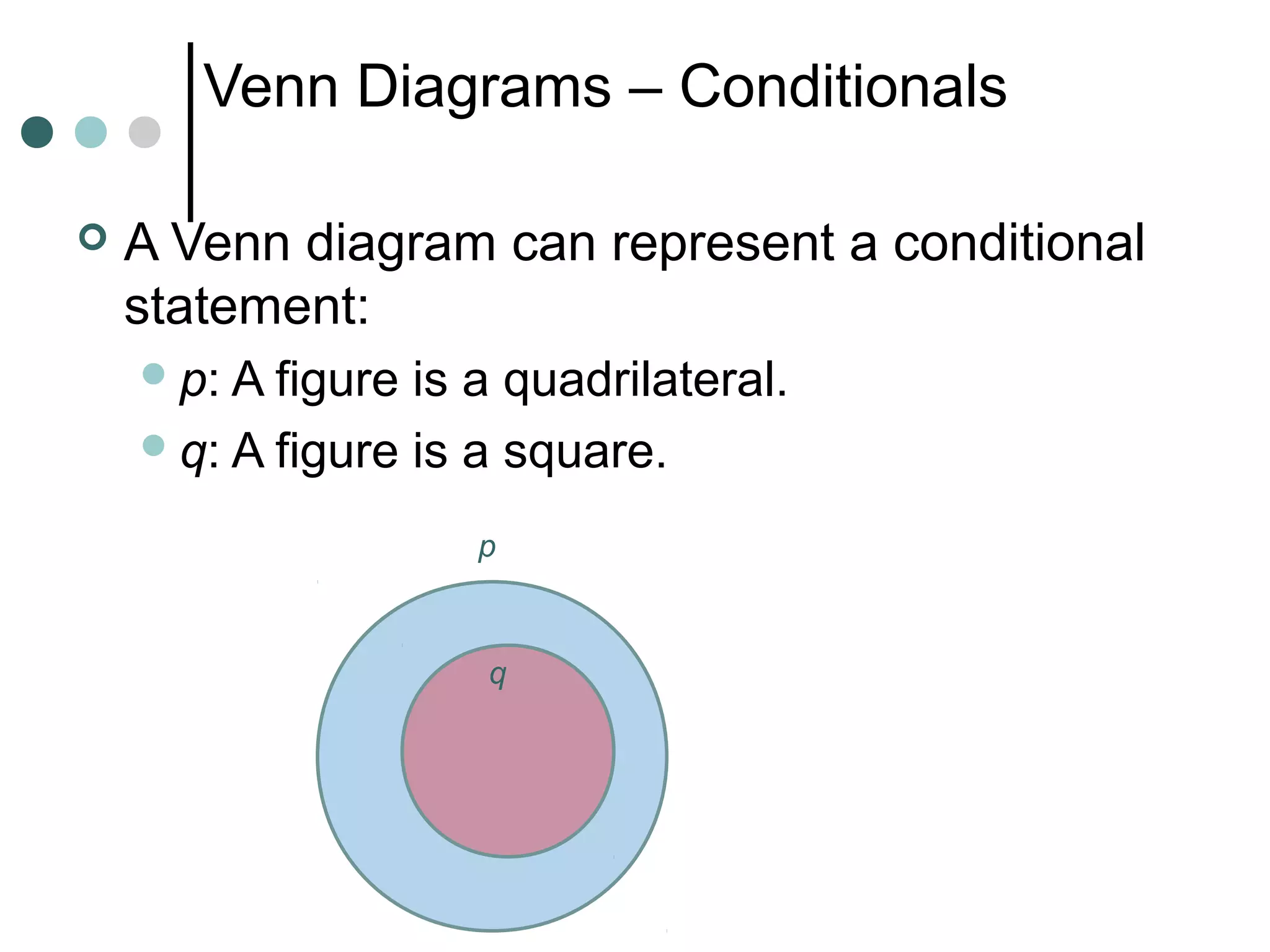
Inductive reasoning uses examples and observations to reach a conclusion, called a conjecture. A conjecture is either always true or false. While examples can support a conjecture, they cannot prove it. A counterexample can demonstrate that a conjecture is false.