Modified booth

MODIFIED BOOTH MULTIPLIERS WITH A REGULAR
PARTIAL PRODUCT ARRAY
CONTENTS
ABSTRACT i
LIST OF FIGURES ii
LIST OF TABLES iii
CHAPTER NO DESCRIPTION PAGE NO
CHAPTER:1 INTRODUCTION 1-8
1.1 CONVENTIONAL MBE MULTIPLIER 3-4
1.2 PROPOSED MULTIPLIER 5-7
1.3 PROPOSED POSTTRUNCATED MBE MULTIPLIER 8
CHAPTER:2 LITERATURE REVIEW 9-13
2.1 ARITHEMATIC AND LOGIC OPERATIONS 9
2.1.1 BOOLEAN ADDITION 9
2.2 BOOLEAN SUBTRACTION 10
2.3 OVERFLOW 11
2.4 MIPS OVERFLOW HANDLING 12
2.5 LOGICAL OPERATIONS 13-14
CHAPTER:3 ARITHMATIC LOGIC UNITS AND MIPS ALU 15-19
3.1 INTRODUCTION 15
3.1.1 BASIC CONCEPTS OF ALU DESIGN 15
3.1.2 1-BIT ALU DESIGN 15
3.2 AND/OR OPERATIONS 15
3.3 FULL ADDER 16-18
3.4 32-BIT ALU DESIGN 19

CHAPTER:4 MIPS ALU 20-29
4.1 SUPPORT FOR THE SLT INSTRUCTION 21
4.2 SUPPORT FOR THE BNE INSTRUCTION 22
4.3 SUPPORT FOR THE SHIFT INSTRUCTION
4.4 SUPPORT FOR THE IMMEDIATE INSTRUCTION 23
4.5 ALU PERFORMANCE ISSUES 24-28
4.6 SUMMARY 29
CHAPTER:5 BOOLEAN MULTIPLICATION AND DIVISION 29-54
5.1MULTIPLIER DESIGN 29-38
5.1.1 DESIGN OF ARITHMETIC DIVISION HARDWARE 39
5.2 UNSIGNED DIVISION 39-41
5.2.1SIGNED DIVISION 41-43
5.2.2DIVISION IN MIPS 44
5.3 FLOATING POINT ARITHMATIC
5.3.1 SCIENTIFIC NOTATION AND FP REPRESENTATION 45
5.3.2 OVERFLOW AND UNDERFLOW 46
5.3.3 IEEE 754 STANDARD 47
5.3.4 FP ARITHMATIC 48-51
5.5 FLOATING POINT IN MIPS 52-54
CHAPTER:6 IMPLEMENTATION 55-58
6.1 EXPERIMENTAL RESULTS 59
6.2 RESULTS FOR POSTTRUNCATED MULTIPLIERS 60
6.3 SIMULATION RESULTANT GRAPH 61
6.3.1 SEMULATION RESULTS FOR 8-BIT MUL 62
CHAPTER:7 PROGRAM CODE 63-71
CONCLUSION 72
REFERENCES

ABSTRACT:
The conventional modified Booth encoding (MBE) generates an irregular partial product
array because of the extra partial product bit at the least significant bit position of each partial product
row. In this brief, a simple approach is proposed to generate a regular partial product array with fewer
partial product rows and negligible overhead, thereby lowering the complexity of partial product
reduction and reducing the area, delay, and power of MBE multipliers. The proposed approach can also
be utilized to regularize the partial product array of post truncated MBE multipliers. Implementation
results demonstrate that the proposed MBE multipliers with a regular partial product array really
achieve significant improvement in area, delay, and power consumption when compared with
conventional MBEmultipliers.

LIST OF FIGURES
S.NO.
FIG
NO.
NAME OF THE FIGURE
PAGE
NO.
1. 3 MBE encoder and selector 5
2. 4 Proposed circuits to generate τi1, di, and α2α1α0 for i = n/2
− 1.
7
3. 5 Example of Boolean addition with carry propagation 10
4. 3.1 Example of a simple 1-bit ALU 16
5.
3.6 Full adder circuit (a) sum-of-products form from above-
listed truth table, (b) Carryout production, and (c) one-bit
full adder with carry
18
6.
3.9 One-bit ALU with three operations: and, or, and addition:
(a) Least significant bit, (b) Remaining bits
19
7. 3.10 32-bit ALU with three operations: and, or, and addition 19
8. 3.10(a) the generic one-bit ALU designed in Sections 3.2.1-3.2.3 20
9. 3.11 One-bit ALU with additional logic for slt operation 22
10.
3.12 32-bit ALU with additional logic to support bne and slt
instructions
23
11. 3.14 Supporting immediate instructions on a MIPS ALU design 25
12. 3.14(a) two-level CLA architecture 27
13.
3.15 Pencil-and-paper multiplication of 32-bit Boolean number
representations: (a) algorithm, and (b) simple ALU circuitry
30-31
14.
3.16 Second version of pencil-and-paper multiplication of 32-bit
Boolean number representations: (a) algorithm, and (b)
schematic diagram of ALU circuitry
32-33
15.
3.17 Third version of pencil-and-paper multiplication of 32-bit
Boolean number representations: (a) algorithm, and (b)
schematic diagram of ALU circuitry
34-35

16.
3.18 Booth's procedure for multiplication of 32-bit Boolean
number representations: (a) algorithm, and (b) schematic
diagram of ALU circuitry
38
17.
3.19 Division of 32-bit Boolean number representations: (a)
algorithm, (b) example using division of the unsigned
integer 7 by the unsigned integer 3, and (c) schematic
diagram of ALU circuitry
40-41
18.
3.20 Division of 32-bit Boolean number representations: (a)
algorithm, and (b,c) examples using division of +7 or -7 by
the integer +3 or -3
42-43
19.
3.21 MIPS ALU supporting the integer arithmetic operations
(+,-,x,/)
44
20. 3.23 MIPS ALU supporting floating point addition 53

LIST OF TABLES
S.NO.
TABLE
NO.
NAME OF THE TABLE
PAGE
NO.
1. 1.1
Conventional MBE partial product arrays for 8 × 8
multiplication
1
2. 1.2
Truth table for MBE TABLE
2
3. 1.3
Proposed MBE partial product array for 8 × 8
multiplication
4
4. 2 truth table for partial product bits in the proposed
partial product array:
6
5. 3 truth table for new sign extension bits 7
6. 3.1 Special values in the IEEE 754 standard 49
7. 4 experimental results of MBE multipliers 59
8. 5 experimental results of post truncated multipliers 60

I. INTRODUCTION
ENHANCING the processing performance and reducing the power dissipation of
the systems are the most important design challenges for multimedia and digital signal
processing (DSP) applications, in which multipliers frequently dominate the system’s
performance and power dissipation. Multiplication consists of three major steps: 1) recoding and
generating partial products; 2) reducing the partial products by partial product reduction schemes
(e.g., Wallace tree [1]–[3]) to two rows; and 3) adding the remaining two rows of partial
products by using a carry-propagate adder (e.g., carry look ahead adder) to obtain the final
product. There are already many techniques developed in the past years for these three steps to
improve the performance of multipliers. In this brief, we will focus on the first step (i.e., partial
product generation) to reduce the area, delay, and power consumption of multipliers. The partial
products of multipliers are generally generated by using two-input AND gates or a modified
Booth encoding(MBE) algorithm [3]–[7]. The latter has widely been adopted in parallel
multipliers since it can reduce the number of partial product rows to be added by half, thus
reducing the size and enhancing the speed of the reduction tree. However, as shown in
Fig. 1. Conventional MBE partial product arrays for 8 × 8 multiplication.

Fig. 1(a), the conventional MBE algorithm generates n/2 + 1partial product rows rather
than n/2 due to the extra partial product bit (neg bit) at the least significant bit position of each
partial product row for negative encoding, leading to an irregular partial product array and a
complex reduction tree. Some approaches [7], [8] have been proposed to generate more regular
partial product arrays, as shown in Fig. 1(b) and (c), for the MBE multipliers. Thus, the area,
delay, and power consumption of the reduction tree, as well as the whole MBE multiplier, can be
reduced. In this brief, we extend the method proposed in [7] to generate a parallelogram-shaped
partial product array, which is more regular than that of [7] and [8]. The proposed approach
reduces the partial product rows from n/2 + 1 to n/2 by incorporating the last neg bit into the sign
extension bits of the first partial product row, and almost no overhead is introduced to the partial
product generator. More regular partial product array and fewer partial product rows result in a
small and fast reduction tree, so that the area, delay, and power of MBE multipliers can further
be reduced. In addition, the proposed approach can also be applied to regularize the partial
product array of post truncated MBE multipliers. Post truncated multiplication, which generates
the 2n-bit product and then rounds the product into n bits, is desirable in many multimedia and
DSP systems due to the fixed register size and bus width inside the hardware.
Experimental results show that the proposed general and post truncated MBE multipliers
with a regular partial product array can achieve significant improvement in area, delay, and
power consumption when compared with conventional MBE multipliers.
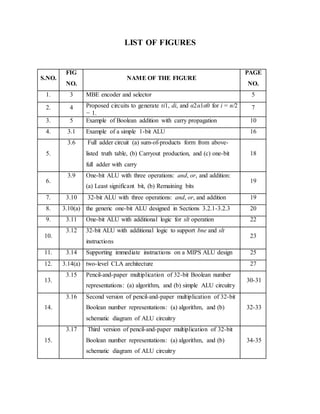
TABLE I
MBE TABLE

1.1. CONVENTIONAL MBEMULTIPLIER
Consider the multiplication of two n-bit integer numbers A (multiplicand) and B (multiplier) in
2’s complement representation,
where b−1 = 0, and mi ∈ {−2,−1, 0, 1, 2}. According to the encoded results from B,
the Booth selectors choose −2A, −A, 0, A, or 2A to generate the partial product rows, as shown in
Table I. The 2A in Table I is obtained by left shifting A one bit. Negation operation is achieved
by complementing each bit of A (one’s complement) and adding “1” to the least significant bit.
Adding “1” is implemented as a correction bit neg, which implies that the partial product row is
negative (neg = 1) or positive (neg = 0). In addition, because partial product rows are represented
in 2’s complement representation and every row is left shifted two bit positions with respect to
the previous row, sign extensions are required to align the most significant parts of partial
product rows. These extra sign bits will significantly complicate the reduction tree. Therefore,
many sign extension schemes [3], [9]–[11] have been proposed to prevent extending up the sign
bit of each row to the (2n − 1)th bit position.
Fig. 1(a) illustrates the MBE partial product array for an 8 × 8 multiplier with a sign
extension prevention procedure, where si is the sign bit of the partial product row PPi, si is the
complement of si, and b_p indicates the bit position. As can beseen in Fig. 1(a), MBE reduces
the number of partial product rows by half, but the correction bits result in an irregular partial
product array and one additional partial product row.

To have a more regular least significant part of each partial product row PPi, the authors in
[7] added the least significant bit pi0 with negi in advance and obtained a new least significant
bit τi0 Fig. 2. Proposed MBE partial product array for 8 × 8 multiplication. and a carry ci. Note
that both τi0 and ci are generated no later than other partial product bits. Fig. 1(b) depicts the 8 ×
8 MBE partial product array generated by the approach proposed in [7]. Since ci is at the left one
bit position of negi, the required additions in the reduction tree are reduced. However, the
approach does not remove the additional partial product row PP4. The problem is overcome in
[8] by directly producing the 2’s complement representation of the last partial product row
PPn/2−1 while the other partial products are produced so that the last neg bit will not be
necessary.
An efficient method and circuit are developed in [8] to find the 2’s complement of the
last partial product row in a logarithmic time. As shown in Fig. 1(c), the 10-bit last partial
product row and its neg bit in Fig. 1(a) are replaced by the 10-bit 2’s complemented partial
products (s3, s3, t7, t6, . . . , t0) without the last neg bit. Note that one extra “1” is added at the
fourteenth bit position to obtain the correct final product. The approach simplifies and speeds up
the reduction step, particularly for a multiplier that is in the size of a power of 2 and uses 4–2
compressors [12], [13] to achieve modularity and high performance. However, the approach
must additionally develop and design the 2’s complement logic, which possibly enlarges the area
and delay of the partial product generator and lessens the benefit contributed by removing the
extra row.

1.2.PROPOSED MULTIPLIERS
The proposed MBE multiplier combines the advantages of these two approaches presented in [7]
and [8] to produce a very regular partial product array, as shown in Fig. 2. In the partial product
array, not only each negi is shifted left and replaced by ci but also the last neg bit is removed by
using a simple approach described in detail in the following section. A. Proposed MBE
Multiplier For MB recoding, at least three signals are needed to represent the digit set {−2,−1, 0,
1, 2}. Many different ways have been developed, and Table I shows the encoding scheme
proposed in [14] that is adopted to implement the proposed MBEmultiplier. The Booth encoder
and selector circuits proposed in [14] are depicted in Fig. 3(a) and (b), respectively. Based on the
recoding scheme and the approach proposed in [7], τi0 and ci in Fig. 1(b) can be derived from
the truth table shown in Table II, as follows:
τi0 =onei · a0 = onei + a0------------------------------ (3)
ci =negi · (onei + a0) = negi + onei · a0.------------------------- (4)
Fig. 3. MBE encoder and selector proposed in [14].

TABLE II
TRUTH TABLE FOR PARTIAL PRODUCT BITS IN THE PROPOSED PARTIAL
PRODUCT ARRAY:
According to (3) and (4), τi0 and ci can be produced by one NOR gate and one AOI gate,
respectively. Moreover, they are generated no later than other partial product bits. To further
remove the additional partial product row PPn/2 [i.e., PP4 in Fig. 1(b)], we combine the ci for i =
n/2 − 1 with the partial product bit pi1 to produce a new partial product bit τi1 and a new carry
di. Then, the carry di can be incorporated into the sign extension bits of PP0. However, if τi1 and
di are produced by adding ci and pi1, their arrival delays will probably be larger than other
partial product bits. Therefore, we directly produce τi1 and di for i = n/2 − 1 from A, B, and the
outputs of the Booth encoder (i.e., negi, twoi, and onei), as shown in Table II, where L and £
denote the Exclusive-OR and Exclusive-NOR operations, respectively.
The logic expressions of τi1 and di can be written as
τi1 =onei · ε + twoi · a0 = (onei + ε) · (twoi + a0) ---------------------------- (5)
di =(b2i+1 + a0) · [(b2i−1 + a1) · (b2i + a1) · (b2i + b2i−1)]-----------------------(6)
where
ε = La1, if a0 · b2i+1 = 0
a1, otherwise. --------------------(7)

Since the weight of di is 2n, which is equal to the weight of s0 at bit position n, di can be
incorporated with the sign extension bits s0s0s0 of PP0. Let α2α1α0 be the new bits after
incorporating di into s0s0s0; the relations between them are summarized in Table III. As can be
seen in Table III, the maximal value of s0s0s0 is 100 so that the addition of s0s0s0 and di will
never produce an overflow. Therefore, α2α1α0 is
TABLE III
TRUTH TABLE FOR NEW SIGN EXTENSION BITS:
Fig. 4. Proposed circuits to generate τi1, di, and α2α1α0 for i = n/2 − 1.
enough to represent the sum of s0s0s0 and di. According to
Table III, α2, α1, and α0 can be expressed as
α2 =(s0 · di) -----------------------(8)
α1 =s0 · di = α2------------------------------ (9)
α0 =s0£ di. --(10)
The corresponding circuits to generate τi1, di, and α2α1α0 are depicted in Fig. 4(a)–(c),
respectively. The partial product array generated by the proposed approach for the 8 × 8
multiplier is shown in Fig. 2. This regular array is generated by only slightly modifying the
original partial product generation circuits and introducing almost no area and delay overhead.

1.3. Proposed Post truncated MBE Multiplier
As mentioned earlier, the product of an n × n multiplier is frequently rounded to n bits. A
post truncated multiplier can be accomplished by adding a “1” at the (n − 1)th bit position of the
partial product array and then truncating the least significant n-bit of the final 2n-bit product, as
shown in Fig. 5(a). Unfortunately, this extra “1” will result in one additional partial product row
like negn/2−1, and it cannot be removed by directly producing the 2’s complement
representation of the last partial product row PPn/2−1. On the other hand, the proposed approach
to remove negn/2−1 can easily be extended to simultaneously remove this extra “1.” Because the
weight of the extra “1” is equal to the weight of pi1 for i = n/2 − 1, we add the two least
significant bits pi1pi0 with the extra “1” and negn/2−1 beforehand to obtain a 2-bit sum ˜τi1τi0
and a carry ei. τi0 can be generated according to (3). Similar to τi1 and di, ˜τi1 and ei for i = n/2
− 1 are directly produced from A, B, and the outputs of the Booth encoder to shorten their arrival
delays. The relations between them are also listed in Table II, and ˜τi1 and ei can be obtained as
follows: ˜

τi1 =τi1------------------------- (11)
ei =(κ + onei) · (π + onei)------------------------- (12)
Where
κ = (b2n+1 · b2n · a0 + b2n+1 · b2n) ------------- (13)
π =b2n+1 · a1 · a0 + b2n+1 · a1. ------------------------ (14)
Subsequently, the carry ei must also be incorporated with the sign extension bits s0s0s0 of PP0
to remove the additional partial product row. Let β2β1β0 be the result of incorporating ei into
s0s0s0; they can be obtained by the similar method as α2α1α0 shown in (8)–(10). The partial
product array generated by the is shown in Fig. 5(b).
2. LETERATURE REVIEW
2.1. Arithmetic and Logic Operations
The ALU is the core of the computer - it performs arithmetic and logic operations on data that
not only realize the goals of various applications (e.g., scientific and engineering programs), but
also manipulate addresses (e.g., pointer arithmetic). In this section, we will overview algorithms
used for the basic arithmetic and logical operations. A key assumption is that twos complement
representation will be employed, unless otherwise noted.
2.1.1. Boolean Addition
When adding two numbers, if the sum of the digits in a given position equals or exceeds the
modulus, then a carry is propagated. For example, in Boolean addition, if two ones are added,
the sum is obviously two (base 10), which exceeds the modulus of 2 for Boolean numbers (B =
Z2 = {0,1}, the integers modulo 2). Thus, we record a zero for the sum and propagate a carry
valued at one into the next more significant digit, as shown in Figure 3.1.

Figure 3.1. Example of Boolean addition with carry propagation, adapted from [Maf01].
2.2. Boolean Subtraction
When subtracting two numbers, two alternatives present themselves. First, one can
formulate a subtraction algorithm, which is distinct from addition. Second, one can negate the
subtrahend (i.e., in a - b, the subtrahend is b) then perform addition. Since we already know how
to perform addition as well as twos complement negation, the second alternative is more
practical. Figure 2.2 illustrates both processes, using the decimal subtraction 12 - 5 = 7 as an
example.

Example of Boolean subtraction using (a) unsigned binary representation, and (b) addition
with twos complement negation - adapted from [Maf01].
Just as we have a carry in addition, the subtraction of Boolean numbers uses a borrow. For
example, in Figure 2.2a, in the first (least significant) digit position, the difference 0 - 1 in the
one's place is realized by borrowing a one from the two's place (next more significant digit). The
borrow is propagated upward (toward the most significant digit) until it is zeroed (i.e., until we
encounter a difference of 1 - 0).
2.3. Overflow
Overflow occurs when there are insufficient bits in a binary number representation to portray the
result of an arithmetic operation. Overflow occurs because computer arithmetic is not closed
with respect to addition, subtraction, multiplication, or division. Overflow cannot occur in
addition (subtraction), if the operands have different (resp. identical) signs.
To detect and compensate for overflow, one needs n+1 bits if an n-bit number representation is
employed. For example, in 32-bit arithmetic, 33 bits are required to detect or compensate for
overflow. This can be implemented in addition (subtraction) by letting a carry (borrow) occur
into (from) the sign bit. To make a pictorial example of convenient size, Figure 3.3 illustrates the

four possible sign combinations of differencing 7 and 6 using a number representation that is
four bits long (i.e., can represent integers in the interval [-8,7]).
Example of overflow in Boolean arithmetic, adapted from [Maf01].
2.4. MIPS Overflow Handling
MIPS raises an exception when overflow occurs. Exceptions (or interrupts) act like procedure
calls. The register $epc stores the address of the instruction that caused the interrupt, and the
instruction
mfc register, $epc
moves the contents of $epc to register. For example, register could be $t1. This is an efficient
approach, since no conditional branch is needed to test for overflow.
Two's complement arithmetic operations (add, addi, and sub instructions) raise exceptions on
overflow. In contrast, unsigned arithmetic (addu and addiu) instructions do not raise an
exception on overflow, since they are used for arithmetic operations on addresses (recall our
discussion of pointer arithmetic in Section 2.6). In terms of high-level languages, C ignores
overflows (always uses addu, addiu, and subu), while FORTRAN uses the appropriate

instruction to detect overflow. Figure 3.4 illustrates the use of conditional branch on overflow for
signed and unsigned addition operations.
Example of overflow in Boolean arithmetic, adapted from [Maf01].
2.5. Logical Operations
Logical operations apply to fields of bits within a 32-bit word, such as bytes or bit fields (in C, as
discussed in the next paragraph). These operations include shift-left and shift-right operations
(sll and srl), as well as bitwise and, or (and, andi, or, ori). As we saw in Section 2, bitwise
operations treat an operand as a vector of bits and operate on each bit position.
C bit fields are used, for example, in programming communications hardware, where
manipulation of a bit stream is required. In Figure 3.5 is presented C code for an example
communications routine, where a structure called receiver is formed from an 8-bit field called
receivedByte and two one-bit fields called ready and enable. The C routine sets receiver.ready
to 0 and receiver.enable to 1.

Figure 2.5. Example of C bit field use in MIPS, adapted from [Maf01].
Note how the MIPS code implements the functionality of the C code, where the state of the
registers $s0 and $s1 is illustrated in the five lines of diagrammed register contents below the
code. In particular, the initial register state is shown in the first two lines. The sll instruction
loads the contents of $s1 (the receiver) into $s0 (the data register), and the result of this is shown
on the second line of the register contents. Next, the srl instruction left-shifts $s0 24 bits,
thereby discarding the enable and ready field information, leaving just the received byte. To
signal the receiver that the data transfer is completed, the andi and ori instructions are used to
set the enable and ready bits in $s1, which corresponds to the receiver. The data in $s0 has
already been received and put in a register, so there is no need for its further manipulation.

3. ALU AND MIPS ALU
3.1. Arithmetic Logic Units and the MIPS ALU
In this section, we discuss hardware building blocks, ALU design and implementation, as well as
the design of a 1-bit ALU and a 32-bit ALU. We then overview the implementation of the MIPS
ALU.
3.1.1. Basic Concepts of ALU Design
ALUs are implemented using lower-level components such as logic gates, including and, or, not
gates and multiplexers. These building blocks work with individual bits, but the actual ALU
works with 32-bit registers to perform a variety of tasks such as arithmetic and shift operations.
In principle, an ALU is built from 32 separate 1-bit ALUs. Typically, one constructs separate
hardware blocks for each task (e.g., arithmetic and logical operations), where each operation is
applied to the 32-bit registers in parallel, and the selection of an operation is controlled by a
multiplexer. The advantage of this approach is that it is easy to add new operations to the
instruction set, simply by associating an operation with a multiplexer control code. This can be
done provided that the mux has sufficient capacity. Otherwise, new data lines must be added to
the mux (es), and the CPU must be modified to accomodate these changes.
3.1.2. 1-bit ALU Design
As a result, the ALU consists of 32 muxes (one for each output bit) arranged in parallel to send
output bits from each operation to the ALU output.
3.2. And/Or Operations. As shown in Figure 3.6, a simple (1-bit) ALU operates in parallel,
producing all possible results that are then selected by the multiplexer (represented by an oval
shape at the output of the and / or gates. The output C is thus selected by the multiplexer. (Note:
If the multiplexer were to be applied at the input(s) rather than the output, twice the amount of
hardware would be required, because there are two inputs versus one output.)

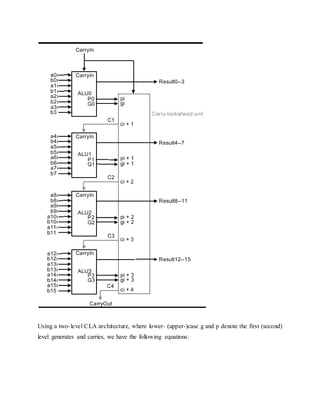
Figure 3.6. Example of a simple 1-bit ALU, where the oval represents a multiplexer with a
control code denoted by Op and an output denoted by C - adapted from [Maf01].
3.3. Full Adder. Now let us consider the one-bit adder. Recalling the carry situation shown in
Figure 3.1, we show in Figure 3.7 that there are two types of carries - carry in (occurs at the
input) and carry out (at the output).
Figure 3.7. Carry-in and carry-out in Boolean addition, adapted from [Maf01].
Here, each bit of addition has three input bits (Ai, Bi, and CarryIni), as well as two output bits
(Sumi, CarryOuti), where CarryIni+1 = CarryOuti. (Note: The "i" subscript denotes the i-th bit.)
This relationship can be seen when considering the full adder's truth table, shown below:

Given the four one-valued results in the truth table, we can use the sum-of-products method to
construct a one-bit adder circuit from four three-input and gates and one four-input or gate, as
shown in Figure 3.8a. The CarryOut calculation can be similarly implemented with three two-
input and gates and one three-input or gate, as shown in Figure 3.8b. These two circuits can be
combined to effect a one-bit full adder with carry, as shown in Figure 3.8c.
(a) (b)

(c)
Figure 3.7. Full adder circuit (a) sum-of-products form from above-listed truth table, (b)
CarryOut production, and (c) one-bit full adder with carry - adapted from [Maf01].
Recalling the symbol for the one-bit adder, we can add an addition operation to the one-bit ALU
shown in Figure 3.6. This is done by putting two control lines on the output mux, and by having
an additional control line that inverts the b input (shown as "Binvert") in Figure 3.9).

(a) (b)
Figure 3.9. One-bit ALU with three operations: and, or, and addition: (a) Least significant bit,
(b) Remaining bits - adapted from [Maf01].
3.4. 32-bit ALU Design
The final implementation of the preceding technique is in a 32-bit ALU that incorporates the
and, or, and addition operations. The 32-bit ALU can be simply constructed from the one-bit
ALU by chaining the carry bits, such that CarryIni+1 = CarryOuti, as shown in Figure 3.10.
Figure 3.10. 32-bit ALU with three operations: and, or, and addition - adapted from [Maf01].

This yields a composite ALU with two 32-bit input vectors a and b, whose i-th bit is denoted by
ai and bi, where i = 0..31. The result is also a 32-bit vector, and there are two control buses - one
for Binvert, and one for selecting the operation (using the mux shown in Figure 3.9). There is
one CarryOut bit (at the bottom of Figure 3.10), and no CarryIn.
We next examine the MIPS ALU and how it supports operations such as shifting and branching.
4.MIPS ALU
4.1. MIPS ALU Design
We begin by assuming that we have the generic one-bit ALU designed in Sections 3.2.1-3.2.3,
and shown below:
Here, the Bnegate input is the same as the Binvert input in Figure 3.9, and we assume that we
have three control inputs to the mux whose control line configuration is associated with an
operation, as follows:

4.1. Support for the slt Instruction. The slt instruction (set on less-than) has the following
format:
slt rd, rs, rt
where rd = 1 if rs < rt, and rd = 0 otherwise.
Observe that the inputs rs and rt can represent high-level language input variables A and B. Thus,
we have the following implication:
A < B => A - B < 0 ,
which is implemented as follows:
Step 1. Perform subtraction using negation and a full adder
Step 2. Check most significant bit (sign bit)
Step 3. Sign bit tells us whether or not A < B
To implement slt, we need (a) new input line called Less that goes directly to the mux, and (b) a
new control code (111) to select the slt operation. Unfortunately, the result for slt cannot be
taken directly as the output from the adder. Instead, we need a new output line called Set that is
used only for the slt instruction. Overflow detection logic is also associated with this bit. The
additional logic that supports slt is shown in Figure 3.11.

Figure 3.11. One-bit ALU with additional logic for slt operation - adapted from [Maf01].
Thus, for a 32-bit ALU, the additional cost of the slt instruction is (a) augmentation of each of
32 muxes to have three control lines instead of two, (b) augmentation of each of 32 one-bit
ALU's control signal structure to have an additional (Less) input, and (c) the addition of overflow
detection circuitry, a Set output, and an xor gate on the output of the sign bit.
4.2. Support for the bne Instruction. Recall the branch-on-not-equal instruction bne r1, r2,
Label, where r1 and r2 denote registers and Label is a branch target label or address. To
implement bne, we observe that the following implication holds:
A - B = 0 => A = B .
then add hardware to test if the comparison between A and B implemented as (A - B) is zero.
Again, this can be done using negation and the full adder that we have already designed as part
of the ALU. The additional step is to or all 32 results from each of the one-bit ALUs, then invert

the output of the or operation. Thus, if all 32 bits from the one-bit full adders are zero, then the
output of the or gate will be zero (inverted, it will be one). Otherwise, the output of the or gate
wil be one (inverted, it will be zero). We also need to consider A - B, to see if there is overflow
when A = 0. A block diagram of the hardware modification is shown in Figure 3.12.
Figure 3.12. 32-bit ALU with additional logic to support bne and slt instructions - adapted from
[Maf01].
Here, the additional hardware involves 32 separate output lines from the 342 one-bit adders, as
well as a cascade of or gates to implement a 32-input nor gate (which doesn't exist in practice,
due to excessive fan-in requirement).
4.3. Support for Shift Instructions. Considering the sll, srl, and sra instructions, these are
supported in the ALU under design by adding a data line for the shifter (both left and right).

However, the shifters are much more easily implemented at the transistor level (e.g., outside the
ALU) rather than trying to fit more circuitry onto the ALU itself.
In order to implement a shifter external to the ALU, we consider the design of a barrel shifter,
shown schematically in Figure 3.13. Here, the closed siwtch pattern, denoted by black filled
circles, is controlled by the CPU through control lines to a mux or decoder. This allows data line
xi to be sent to output xj, where i and j can be unequal.
Figure 3.13. Four bit barrel shifter, where "x >> 1" denotes a shift amount greater than one -
adapted from [Maf01].
This type of N-bit shifter is well understood and easy to construct, but has space complexity of
O(N2).
4.4. Support for Immediate Instructions. In the MIPS immediate instruction formats, the first
input to the ALU is the first register (we'll call it rs) in the immediate command, while the
second input is either data from a register rt or a zero or sign-extended constant (immediate). To
support this type of instruction, we need to add a mux at the second input of the ALU, as shown
in Figure 3.14. This allows us to select whether rt or the sign-extended immediate is input to the
ALU.

Figure 3.14. Supporting immediate instructions on a MIPS ALU design, where IR denotes the
instruction register, and (/16) denotes a 16-bit parallel bus - adapted from [Maf01].
4.5 ALU Performance Issues
When estimating or measuring ALU performance, one wonders if a 32-bit ALU is as fast as a 1-
bit ALU - what is the degree of parallelism, and do all operations execute in parallel? In practice,
some operations on N-bit operands (e.g., addition with sequential propagation of carries) take
O(N) time. Other operations, such as bitwise logical operations, take O(1) time. Since addition
can be implemented in a variety of ways, each with a certain level of parallelism, it is wise to
consider the possibility of a full adder being a computational bottleneck in a simple ALU.
We previously discussed the ripple-carry adder (Figure 3.10) that propagates the carry bit from
stage i to stage i+1. It is readily seen that, for an N-bit input, O(N) time is required to propagate
the carry to the most significant bit. In contrast, the fastest N-bit adder uses O(log2N) stages in a

tree-structured configuration with N-1 one-bit adders. Thus, the complexity of this technique is
O(log2N) work. In a sequential model of computation, this translates to O(log2N) time. If one is
adding smaller numbers (e.g., up to 10-bit integers with current memory technology), then a
lookup table can be used that (1) forms a memory address A by concatenating binary
representations of the two operands, and (2) produces a result stored in memory that is accessed
using A. This takes O(1) time, that is dependent upon memory bandwidth.
An intermediate approach between these extremes is to use a carry-lookahead adder (CLA).
Suppose we do not know the value of the carry-in bit (which is usually the case). We can express
the generation (g) of a carry bit for the i-th position of two operands a and b, as follows:
gi = ai bi ,
where the i-th bits of a and b are and-ed. Similarly, the propagated carry is expressed as:
pi = ai + bi ,
where the i-th bits of a and b are or-ed. This allows us to recursively express the carry bits in
terms of the carry-in c0, as follows:
Did we get rid of the ripple? (Well, sort of...) What we did was transform the work involved in
carry propagation from the adder circuitry to a large equation for cN. However, this equation
must still be computed in hardware. (Lesson: In computing, you don't get much for free.)
Unfortunately, it is prohibitively costly to build a CLA circuit for operands as large as 16 bits.
Instead, we can use the CLA principle to create a two-tiered circuit, for example, at the bottom
level an array of four 4-bit full adders (economical to construct), connected at the top level by a
CLA, as shown below:

Using a two-level CLA architecture, where lower- (upper-)case g and p denote the first (second)
level generates and carries, we have the following equations:

P0 = p3 + p2 + p1 + p0
P1 = p7 + p6 + p5 + p4
P2 = p11 + p10 + p9 + p8
P3 = p15 + p14 + p13 + p12
G0 = g3 + p3g2 + p3p2g1 + p3p2p1g0
G1 = g7 + p7g6 + p7p6g5 + p7p6p5g4
G2 = g11 + p11g10 + p11p10g9 + p11p10p9g8
G3 = g15 + p15g14 + p15p14g13 + p15p14p13g12
Assuming that and as well as or gates have the same propagation delay, comparative analysis of
the ripple carry vs. carry lookahead adders reveals that the total time to compute a CLA result is
the summation of all gate delays along the longest path through the CLA. In the case of the 16-
bit adder exemplified above, the CarryOut signals c16 and C4 define the longest path. For the
ripple carry adder, this path has length 2(16) = 32.
For the two-level CLA, we get two levels of logic in terms of the architecture (P and G versus p
and g). Pi is specified in one level of logic using pi. Gi is specified in one level of logic using pi
and gi. Also, pi and gi each represent one level of logic computed in terms of inputs ai and bi.
Thus, the CLA critical path length is 2 + 2 + 1 = 5, which means that two-level 16-bit CLA is 6.4
= 32/5 times faster than a 16-bit ripple carry adder.
It is also useful to note that the logic equation for a one-bit adder can be expressed more simply
with xor logic, for example:
A + B = A xor B xor CarryIn .
In some technologies, xor is more efficient than and/or gates. Also, processors are now designed
in CMOS technology, which allows fewer muxes (this also applies to the barrel shifter).
However, the design principles are similar.

4.6. Summary
We have shown that it is feasible to build an ALU to support the MIPS ISA. The key idea is to
use a multiplexer to select the output from a collection of functional units operating in parallel.
We can replicate a 1-bit ALU that uses this principle, with appropriate connections between
replicates, to produce an N-bit ALU.
Important things to remember about ALUs are: (a) all of the gates are working in parallel, (b) the
speed of a gate is affected by the number of inputs (degree of fan-in), and (c) the speed of a
circuit depends on the number of gates in the longest computational path through the circuit (this
can vary per operation). Finally, we have shown that changes in architectural organization can
improve performance, similar to better algorithms in software.
5.1. Boolean Multiplication and Division
Multiplication is more complicated than addition, being implemented by shifting as well as
addition. Because of the partial products involved in most multiplication algorithms, more time
and more circuit area is required to compute, allocate, and sum the partial products to obtain the
multiplication result.
5.1. Multiplier Design
We herein discuss three versions of the multiplier design based on the pencil-and-paper
algorithm for multiplication that we all learned in grade school, which operates on Boolean
numbers, as follows:
Multiplicand: 0010 # Stored in register r1
Multiplier: x 1101 # Stored in register r2
--------------------
Partial Prod 0010 # No shift for LSB of Multiplier
" " 0000 # 1-bit shift of zeroes (can omit)
" " 0010 # 2-bit shift for bit 2 of Multiplier
" " 0010 # 3-bit shift for bit 3 of Multiplier
-------------------- # Zero-fill the partial products and add
PRODUCT 0011010 # Sum of all partial products -> r3

(b)
Figure 3.15. Pencil-and-paper multiplication of 32-bit Boolean number representations: (a)
algorithm, and (b) simple ALU circuitry - adapted from [Maf01].
The second version of this algorithm is shown in Figure 3.16. Here, the product is shifted with
respect to the multiplier, and the multiplicand is shifted after the product register has been
shifted. A 64-bit register is used to store both the multiplicand and the product.

(b)
Figure 3.16. Second version of pencil-and-paper multiplication of 32-bit Boolean number
representations: (a) algorithm, and (b) schematic diagram of ALU circuitry - adapted from
[Maf01].
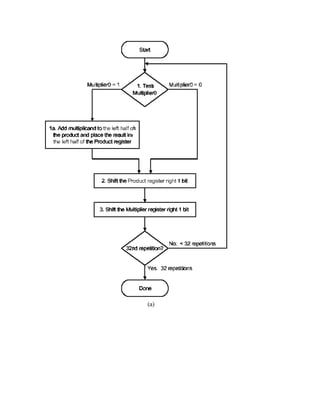
The final version puts results in the product register if and only if the least significant bit of the
product produced on the previous iteration is one-valued. The product register only is shifted.
This reduces by approximately 50 percent the amount of shifting that has to be done, which
reduces time and hardware requirements. The algorithm and ALU schematic diagram is shown in
Figure 3.17.

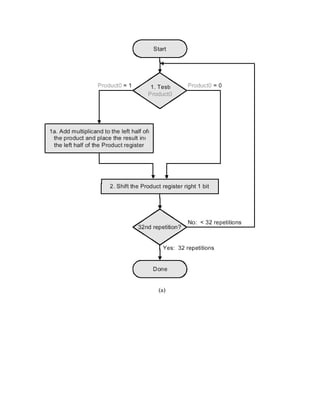
(b)
Figure 3.17. Third version of pencil-and-paper multiplication of 32-bit Boolean number
representations: (a) algorithm, and (b) schematic diagram of ALU circuitry - adapted from
[Maf01].
Thus, we have the following shift-and-add scheme for multiplication:
The preceding algorithms and circuitry does not hold for signed multiplication, since the
bits of the multiplier no longer correspond to shifts of the multiplicand. The following example is
illustrative:

A solution to this problem is Booth's Algorithm, whose flowchart and corresponding
schematic hardware diagram are shown in Figure 3.18. Here, the examination of the multiplier is
performed with look ahead toward the next bit. Depending on the bit configuration, the
multiplicand is positively or negatively signed, and the multiplier is shifted or unshifted.

(a)
(b)
Figure 3.18. Booth's procedure for multiplication of 32-bit Boolean number representations: (a)
algorithm, and (b) schematic diagram of ALU circuitry - adapted from [Maf01].

Observe that Booth's algorithm requires only the addition of a subtraction step and the
comparison operations for the two-bit codes, versus the one-bit comparison in the preceding
three algorithms. An example of Booth's algorithm follows:
Here N = 4 iterations of the loop are required to produce a product from two N = 4 digit
operands. Four shifts and two subtractions are required. From the analysis of the algorithm
shown in Figure 3.18a, it is easily seen that the maximum work for multiplying two N-bit
numbers is given by O(N) shift and addition operations. From this, the worst-case computation
time can be computed given CPI for the shift and addition instructions, as well as cycle time of
the ALU.
5.1.1. Designof Arithmetic Division Hardware
Division is a similar operation to multiplication, especially when implemented using a procedure
similar to the algorithm shown in Figure 3.18a. For example, consider the pencil-and-paper
method for dividing the byte 10010011 by the nybble 1011:

The governing equation is as follows:
Dividend = Quotient �Divisor + Remainder .
5.2. Unsigned Division. The unsigned division algorithm that is similar to Booth's algorithm is
shown in Figure 3.19a, with an example shown in Figure 3.19b. The ALU schematic diagram in
given in Figure 3.19c. The analysis of the algorithm and circuit is very similar to the preceding
discussion of Booth's algorithm.

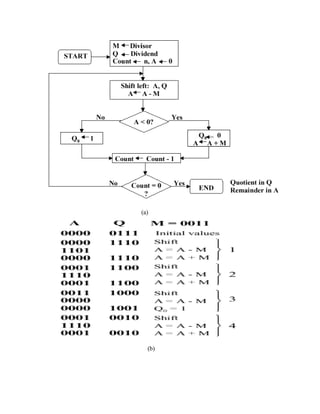
(c)
Figure 3.19. Division of 32-bit Boolean number representations: (a) algorithm, (b) example
using division of the unsigned integer 7 by the unsigned integer 3, and (c) schematic diagram of
ALU circuitry - adapted from [Maf01].
5.2.1. Signed Division. With signed division, we negate the quotient if the signs of the divisor
and dividend disagree. The remainder and the dividend must have the same signs. The governing
equation is as follows:
Remainder = Dividend - (Quotient �Divisor) ,

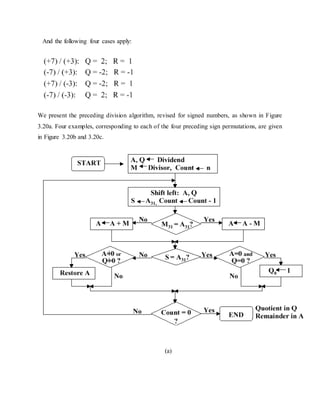
And the following four cases apply:
We present the preceding division algorithm, revised for signed numbers, as shown in Figure
3.20a. Four examples, corresponding to each of the four preceding sign permutations, are given
in Figure 3.20b and 3.20c.
(a)

(b)
(c)
Figure 3.20. Division of 32-bit Boolean number representations: (a) algorithm, and (b,c)
examples using division of +7 or -7 by the integer +3 or -3; adapted from [Maf01].

5.2.2. Division in MIPS. MIPS supports multiplication and division using existing hardware,
primarily the ALU and shifter. MIPS needs one extra hardware component - a 64-bit register
able to support sll and sra instructions. The upper (high) 32 bits of the register contains the
remainder resulting from division. This is moved into a register in the MIPS register stack (e.g.,
$t0) by the mfhi command. The lower 32 bits of the 64-bit register contains the quotient
resulting from division. This is moved into a register in the MIPS register stack by the mflo
command.
In MIPS assembly language code, signed division is supported by the div instruction and
unsigned division, by the divu instruction. MIPS hardware does not check for division by zero.
Thus, divide-by-zero exception must be detected and handled in system software. A similar
comment holds for overflow or underflow resulting from division.
Figure 3.21 illustrates the MIPS ALU that supports integer arithmetic operations (+,-,x,/).
Figure 3.21. MIPS ALU supporting the integer arithmetic operations (+,-,x,/), adapted from
[Maf01].

5.3. Floating Point Arithmetic
Floating point (FP) representations of decimal numbers are essential to scientific computation
using scientific notation. The standard for floating point representation is the IEEE 754 Standard.
In a computer, there is a tradeoff between range and precision - given a fixed number of binary
digits (bits), precision can vary inversely with range. In this section, we overview decimal to FP
conversion, MIPS FP instructions, and how registers are used for FP computations.
We have seen that an n-bit register can represent unsigned integers in the range 0 to 2n-1, as well
as signed integers in the range -2n-1 to -2n-1-1. However, there are very large numbers (e.g.,
3.15576 �1023), very small numbers (e.g., 10-25), rational numbers with repeated digits (e.g., 2/3
= 0.666666...), irrationals such as 21/2, and transcendental numbers such as e = 2.718..., all of
which need to be represented in computers for scientific computation to be supported.
We call the manipulation of these types of numbers floating point arithmetic because the decimal
point is not fixed (as for integers). In C, such variables are declared as the float datatype.
5.3.1. Scientific Notation and FP Representation
Scientific notation has the following configuration:
and can be in normalized form (mantissa has exactly one digit to the left of the decimal point,
e.g., 2.3425 � 10-19) or non-normalized form. Binary scientiic notation has the folowing
configuration, which corresponds to the decimal forms:

Assume that we have the following normal format for scientific notation in Boolean numbers:
+1.xxxxxxx2 �wyyyyy
2 ,
where "xxxxxxx" denotes the significand and "yyyyy" denotes the exponent and we assume that
the number has sign S. This implies the following 32-bit representation for FP numbers:
which can represent decimal numbers ranging from -2.0 �10-38 to 2.0 �1038.
5.3.2.Overflow and Underflow
In FP, overflow and underflow are slightly different than in integer numbers. FP overflow
(underflow) refers to the positive (negative) exponent being too large for the number of bits
alloted to it. This problem can be somewhat ameliorated by the use of double precision, whose
format is shown as follows:
Here, two 32-bit words are combined to support an 11-bit signed exponent and a 52-bit
significand. This representation is declared in C using the double datatype, and can support

numbers with exponents ranging from -30810 to 30810. The primary advantage is greater
precision in the mantissa.
The following chart illustrates specific types of overflow and underflow encountered in standard
FP representation:
5.3.3. IEEE 754 Standard
Both single- and double-precision FP representations are supported by the IEEE 754 Standard,
which is used in the vast majority of computers since its publication in 1980. IEEE 754
facilitates the porting of FP programs, and ensures minimum standards of quality for FP
computer arithmetic. The result is a signed representation - the sign bit is 1 if the FP number
represented by IEEE754 is negative. Otherwise, the sign is zero. A leading value of 1 in the
significand is implicit for normalized numbers. Thus, the significand, which always has a value
between zero and one, occupies 23 + 1 bits in single-precision FP and 52 + 1 bits in double
precision. Zero is represented by a zero significand and a zero exponent - there is no leading
value of one in the significand. The IEEE 754 representation is thus computed as:
FPnumber = (-1)S �(1 + Significand) �2Exponent .
As a parenthetical note, the significand can be translated into decimal values via the following
expansion:

With IEEE 754, it is possible to manipulate FP numbers without having special-purpose FP
hardware. For example, consider the sorting of FP numbers. IEEE 754 facilitates breaking FP
numbers up into three parts (sign, significant, exponent). The numbers to be sorted are ordered
first according to sign (negative < positive), second according to exponent (larger exponent =>
larger number), and third according to significand (when one has at least two numbers with the
same exponents).
Another issue of interest in IEEE 754 is biased notation for exponents. Observe that twos
complement notation does not work for exponents: the largest negative (positive) exponent is
000000012 (111111112). Thus, we must add a bias term to the exponent to center the range of
exponents on the bias number, which is then equated to zero. The bias term is 127 (1023) for the
IEEE 754 single-precision (double-precision) representation. This implies that
FPnumber = (-1)S �(1 + Significand) �2(Exponent - Bias) .
As a result, we have the following example of binary to decimal floating point conversion:
Decimal-to-binary FP conversion is somewhat more difficult. Three cases pertain: (1) the
decimal number can be expressed as a fraction n/d where d is a power of two; (2) the decimal
number has repeated digits (e.g., 0.33333); or (3) the decimal number does not fit either Case 1
or Case 2. In Case 1, one selects the exponent as -log2(d), and converts n to binary notation. Case

3 is more difficult, and will not be discussed here. Case 2 is exemplified in the following
diagram:
Here, the significand is 101 0101 0101 0101 0101 0101, the sign is negative (representation = 1),
and the exponent is computed as 1 + 127 = 12810 = 1000 00002. This yields the following
representation in IEEE 754 standard notation:
The following table summarizes special values that can be represented using the IEEE 754
standard.
Table 3.1. Special values inthe IEEE 754 standard.
Of particular interest in the preceding table is the NaN (not a number) representation. For
example, when taking the square root of a negative number, or when dividing by zero, we
encounter operations that are undefined in the arithmetic operations over real numbers. These
results are called NaNs and are represented with an exponent of 255 and a zero significand.
NaNs can help with debugging, but they contaminate calculations (e.g., NaN + x = NaN). The

recommended approach to NaNs, especially for software designers or engineers early in their
respective careers, is not to use NaNs.
Another variant of FP representation is denormalized numbers, also called denorms. These
number representations were developed to remedy the problem of a gap among representable FP
numbers near zero. For example, the smallest positive number is x = 1.00... � 2-127, and the
second smallest positive number is y = 1.0012 �2-127 = 2-127 + 2-150. This implies that the gap
between zero and x is 2-127 and that the gap between x and y is 2-150, as shown in Figure 3.22a.
(a) (b)
Figure 3.22. Denorms: (a) Gap between zero and 2-127, and (b) Denorms close this gap - adapted
from [Maf01].
This situation can be remedied by omitting the leading one from the significand, thereby
denormalizing the FP representation. The smallest positive number is now the denorm 0.0...1 �
2-127 = 2-150, and the second smallest positive number is 2-149.
5.3.4. FP Arithmetic
Applying mathematical operations to real numbers implies that some error will occur due to the
floating point representation. This is due to the fact that FP addition and subtraction are not
associative, because the FP representation is only an approximation to a real number.

Example 1. Using decimal numbers for clarity, let x = -1.5 �1038, y = 1.5 �1038, and z = 1.0.
With floating point representation, we have:
x + (y + z) = -1.5 �1038 + (1.5 �1038 + 1.0) = 0.0
and
(x + y) + z = (-1.5 �1038 + 1.5 �1038) + 1.0 = 1.0
The difference occurs because the value 1.0 cannot be distinguished in the significand of 1.5 �
1038 due to insufficient precision (number of digits) of the significand in the FP representation of
these numbers (IEEE 754 assumed).
The preceding example leads to several implementational issues in FP arithmetic. Firstly,
rounding occurs when performing math on real numbers, due to lack of sufficient precision. For
example, when multiplying two N-bit numbers, a 2N-bit product results. Since only the upper N
bits of the 2N bit product are retained, the lower N bits are truncated. This is also called
rounding toward zero.
Another type of rounding is called rounding to infinity. Here, if rounding toward +infinity, then
we always round up. For example, 2.001 is rounded up to 3, -2.001 is rounded up to 2.
Conversely, if rounding toward -infinity, then we always round down. For example, 1.999 is
rounded down to 1, -1.999 is rounded down to -2. There is a more familiar technique, for
example, where 3.7 is rounded to 4, and 3.1 is rounded to 3. In this case, we resolve rounding
from n.5 to the nearest even number, e.g., 3.5 is rounded to 4, and -2.5 is rounded to 2.
A second implementational issue in FP arithmetic is addition and subtraction of numbers that
have nonzero significands and exponents. Unlike integer addition, we can't just add the
significands. Instead, one must:
1. Denormalize the operands and shift one of the operands to make the exponents of
both numbers equal (we denote the exponent by E).
2. Add or subtract the significands to get the resulting significand.

3. Normalize the resulting significand and change E to reflect any shifts incurred by
normalization.
We will review several approaches to floating point operations in MIPS in the following section.
5.5. Floating Point in MIPS
The MIPS FP architecture uses separate floating point insturctions for IEEE 754 single and
double precision. Single precision uses add.s, sub.s, mul.s, and div.s, whereas double
precision instructions are add.d, sub.d, mul.d, and div.d. These instructions are much more
complicated than their integer counterparts. Problems with implementing FP arithmetic include
inefficiencies in having different instructions that take significantly different times to execute
(e.g., division versus addition). Also, FP operations require much more hardware than integer
operations.
Thus, in the spirit of RISC design philosophy, we note that (a) a particular datum is not likely to
change its datatype within a program, and (b) some types of programs do not require FP
computation. Thus, in 1990, the MIPS designers decided to separate the FP computations from
the remainder of the ALU operations, and use a separate chip for FP (called the coprocessor). A
MIPS coprocessor contains 32 32-bit registers designated as $f0, $f1, ..., etc. Most of these
registers are specified in the .s and .d instructions. Double precision operands are stored in
register pairs (e.g., $f0,$f1 up to $f30,$f31).
The CPU thus handles all the regular computation, while the coprocessor handles the floating
point operations. Special instructions are required to move data between the coprocessor(s) and
CPU (e.g., mfc0, mtc0, mfc0, mtc0, etc.), where cn refers to coprocessor #n. Similarly, special
I/O operations are required to load and store data between the coprocessor and memory (e.g.,
lwc0, swc0, lwc1, swc1, etc.)
FP coprocessors require very complex hardware, as shown in Figure 3.23, which portrays only
the hardware required for addition.

Figure 3.23. MIPS ALU supporting floating point addition, adapted from [Maf01].
The use of floating point operations in MIPS assembly code is described in the following simple
example, which implements a C program designed to convert Fahrenheit temperatures to Celsius.

Here, we assume that there is a coprocessor c1 connected to the CPU. The values 5.0 and 9.0 are
respectively loaded into registers $f16 and $f18 using the lwc1 instruction with the global
pointer as base address and the variables const5 and const9 as offsets. The single precision
division operation puts the quotient of 5.0/9.0 into $f16, and the remainder of the computation is
straightforward. As in all MIPS procedure calls, the jr instruction returns control to the address
stored in the $ra register.

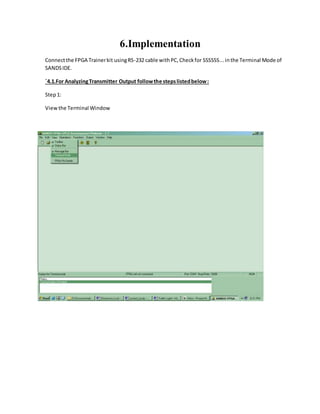
6.Implementation
Connectthe FPGA Trainerkit usingRS-232 cable withPC,Checkfor SSSSSS... inthe Terminal Mode of
SANDSIDE.
`4.1.For AnalyzingTransmitter Output followthe stepslistedbelow:
Step1:
Viewthe Terminal Window

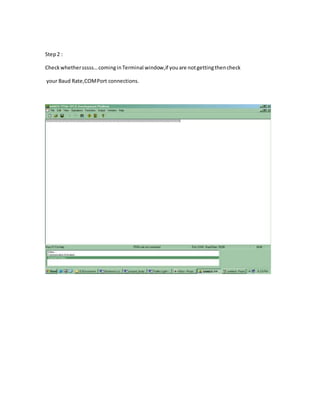
Step2 :
Checkwhethersssss…cominginTerminal window,if youare notgettingthencheck
your Baud Rate,COMPort connections.

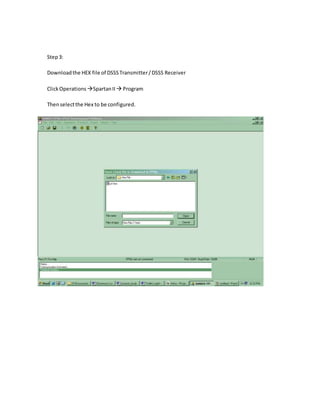
Step3:
Downloadthe HEX file of DSSSTransmitter/DSSS Receiver
ClickOperations SpartanII  Program
Thenselectthe Hex to be configured.

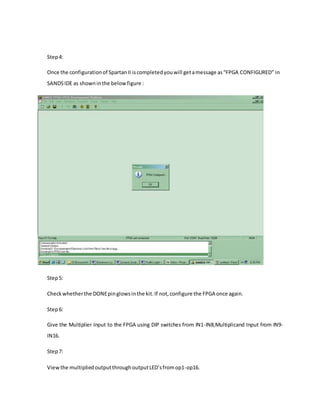
Step4:
Once the configurationof SpartanII iscompletedyouwill getamessage as“FPGA CONFIGURED” in
SANDSIDE as showninthe belowfigure :
Step5:
Checkwhetherthe DONEpinglowsinthe kit.If not,configure the FPGA once again.
Step6:
Give the Multiplier Input to the FPGA using DIP switches from IN1-IN8,Multiplicand Input from IN9-
IN16.
Step7:
Viewthe multipliedoutputthroughoutputLED’sfromop1-op16.

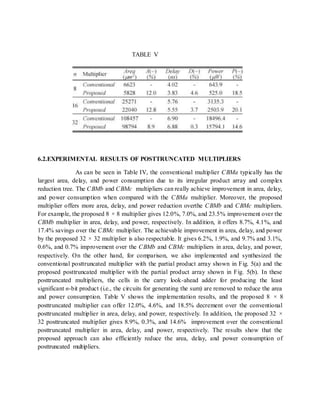
6.1 EXPERIMENTAL RESULTS
For comparison, we have implemented several MBE multipliers whose partial
product arrays are generated by using different approaches. Except for a few of partial product
bits that are generated by different schemes to regularize the partial product array, the other
partial product bits are generated by using the similar method and circuits for all multipliers. In
addition, the partial product array of each multiplier is reduced by a Wallace tree scheme, and a
carry look-ahead adder is used for the final addition. These multipliers were modeled in Verilog
HDL and synthesized by using Synopsys Design Compiler with an Artisan TSMC 0.18-μm 1.8-
V standard cell library. The synthesized netlists were then fed into Cadence SOC Encounter to
perform placement and routing [15]. Delay estimates were obtained after RC extraction from the
placed and routed netlists. Power dissipation was estimated from the same netlists by feeding
them into Synopsys Nanosim to perform full transistor-level power simulation at a clock
frequency of 50 MHz with 5000 random input patterns. The implementation results, including
the hardware area, critical path delay, and power consumption for these multipliers with n = 8,
16, and 32, are listed in Table IV, where CBMa, CBMb [7], and CBMc [8] denote the MBE
multipliers with the partial product array shown in Fig. 1(a)–(c), respectively. Moreover, A(−),
D(−), and P(−) denote the area, delay, andpower decrements when compared with the CBMa
multiplier.
TABLE IV
EXPERIMENTAL RESULTS OF MBEMULTIPLIERS

TABLE V
6.2.EXPERIMENTAL RESULTS OF POSTTRUNCATED MULTIPLIERS
As can be seen in Table IV, the conventional multiplier CBMa typically has the
largest area, delay, and power consumption due to its irregular product array and complex
reduction tree. The CBMb and CBMc multipliers can really achieve improvement in area, delay,
and power consumption when compared with the CBMa multiplier. Moreover, the proposed
multiplier offers more area, delay, and power reduction overthe CBMb and CBMc multipliers.
For example, the proposed 8 × 8 multiplier gives 12.0%, 7.0%, and 23.5% improvement over the
CBMb multiplier in area, delay, and power, respectively. In addition, it offers 8.7%, 4.1%, and
17.4% savings over the CBMc multiplier. The achievable improvement in area, delay, and power
by the proposed 32 × 32 multiplier is also respectable. It gives 6.2%, 1.9%, and 9.7% and 3.1%,
0.6%, and 0.7% improvement over the CBMb and CBMc multipliers in area, delay, and power,
respectively. On the other hand, for comparison, we also implemented and synthesized the
conventional posttruncated multiplier with the partial product array shown in Fig. 5(a) and the
proposed posttruncated multiplier with the partial product array shown in Fig. 5(b). In these
posttruncated multipliers, the cells in the carry look-ahead adder for producing the least
significant n-bit product (i.e., the circuits for generating the sum) are removed to reduce the area
and power consumption. Table V shows the implementation results, and the proposed 8 × 8
posttruncated multiplier can offer 12.0%, 4.6%, and 18.5% decrement over the conventional
posttruncated multiplier in area, delay, and power, respectively. In addition, the proposed 32 ×
32 posttruncated multiplier gives 8.9%, 0.3%, and 14.6% improvement over the conventional
posttruncated multiplier in area, delay, and power, respectively. The results show that the
proposed approach can also efficiently reduce the area, delay, and power consumption of
posttruncated multipliers.

6.4 Simulation graph for 8 bit Multiplier:

7.PROGRAM CODE
module booth_multi_tb ;
wire [15:0] dout ;
reg [7:0] x ;
reg [7:0] y ;
booth_multi
DUT (
.dout (dout ) ,
.x (x ) ,
.y (y ) );
initial
fork
x=8'b00001010;
y=8'b00001010;
join
endmodule
module fulladd (carry,sum,a,b,c);
output carry;
output sum;
input a;
input b;
input c;
assign carry= (a&b)|(a&c)|(c|a);
assign sum = a^b^c;
endmodule
module halfadd (carry,sum,a,b);
output carry;
output sum;
input a;
input b;
assign carry= (a&b);
assign sum = a^b;
endmodule
module negout (b2i1,b2i,b2i_1,aj,aj_1,pij,negi);
input b2i1;
input b2i;
input b2i_1;
input aj;
input aj_1;

output pij;
output negi;
wire onebar;
wire twobar;
assign negi = b2i1 & ((~b2i) | (~b2i_1));
assign w1 = (~b2i1) & b2i & b2i_1;
assign w2 = b2i1 & (~b2i_1) & (~b2i);
assign twobar = ~(w1 | w2);
assign onebar= ~(b2i^b2i_1);
assign w3 = twobar | aj_1;
assign w4 = ~(aj ^b2i1);
assign w5 = w4|onebar;
assign pij = ~(w3 & w5);
endmodule
module neggen (x2i1,x2i,x2i_1,negi);
input x2i1;
input x2i;
input x2i_1;
output negi;
assign negi = x2i1 & ((~x2i) | (~x2i_1));
endmodule
module pij_out(x2i1,x2i,x2i_1,yi,yi_1,pij);
input x2i1;
input x2i;
input x2i_1;
input yi;
input yi_1;
output pij;
assign x1= ~(x2i_1^x2i);
assign z = ~(x2i1 ^ x2i);
assign x2 = x2i_1^x2i;
assign w1= ~(yi^x2i1);
assign w2= ~(yi_1^x2i1);
assign w3= w1 |x1;
assign w4= w2 |z|x2;
assign pij = ~(w3 & w4);
endmodule

module pij_out1 (x2i1,x2i,x2i_1,yi,yi_1,pij);
input x2i1;
input x2i;
input x2i_1;
input yi;
input yi_1;
output pij;
assign onebar = ~(x2i^ x2i_1);
assign w1= ((~x2i1)& x2i & x2i_1);
assign w2= (x2i1& (~x2i) &(~x2i_1));
assign twobar = ~(w1|w2);
assign w3 = twobar|yi_1;
assign w4 = ~(yi^x2i1);
assign w5 = onebar|w4;
assign pij = ~(w3&w4);
endmodule
module pij_out2 (x2i1,x2i,x2i_1,yi,yi_1,pij);
input x2i1;
input x2i;
input x2i_1;
input yi;
input yi_1;
output pij;
assign onebar = (x2i^ x2i_1);
assign w1= ((~x2i1)& x2i & x2i_1);
assign w2= (x2i1& (~x2i) &(~x2i_1));
assign twobar = (w1|w2);
assign w3 = onebar & yi;
assign w4 = yi_1 & twobar;
assign w5 = ~(w3|w4);
assign pij = ~(w5^negi);
endmodule
//------------------ Y x X -----------------------//
module booth_multi (x,y,dout);
input [7:0] y;
input [7:0] x;
output[15:0] dout;
wire [7:0]pp1;

wire [7:0]pp2;
wire [7:0]pp3;
wire [7:0]pp4;
wire [15:0] ppf1;
wire [15:0] ppf2;
wire [15:0] ppf3;
wire [15:0] ppf4;
wire [15:0] const;
wire [3:0]neg;
////////i=0; j=0;
pij_out2 p00(.x2i1(x[1]),
.x2i(x[0]),
.x2i_1(1'b0),
.yi(y[0]),
.yi_1(1'b0),
.pij(pp1[0])
);
////////i=0; j=1;
.x2i(x[0]),
.x2i_1(1'b0),
.yi(y[1]),
.yi_1(y[0]),
.pij(pp1[1])
);
////////i=0; j=2;
.x2i(x[0]),
.x2i_1(1'b0),
.yi(y[2]),
.yi_1(y[1]),
.pij(pp1[2])
);
////////i=0; j=3;
.x2i(x[0]),
.x2i_1(1'b0),
.yi(y[3]),
.yi_1(y[2]),
.pij(pp1[3])
);
.x2i(x[0]),
.x2i_1(1'b0),
.yi(y[4]),
.yi_1(y[3]),
.pij(pp1[4])
);
.x2i(x[0]),

.x2i_1(1'b0),
.yi(y[5]),
.yi_1(y[4]),
.pij(pp1[5])
);
.x2i(x[0]),
.x2i_1(1'b0),
.yi(y[6]),
.yi_1(y[5]),
.pij(pp1[6])
);
.x2i(x[0]),
.x2i_1(1'b0),
.yi(y[7]),
.yi_1(y[6]),
.pij(pp1[7])
);
//--------------------------pp2
////////i=1; j=0;
.x2i(x[2]),
.x2i_1(x[1]),
.yi(y[0]),
.yi_1(1'b0),
.pij(pp2[0])
);
////////i=1; j=1;
.x2i(x[2]),
.x2i_1(x[1]),
.yi(y[1]),
.yi_1(y[0]),
.pij(pp2[1])
);
////////i=1; j=2;
.x2i(x[2]),
.x2i_1(x[1]),
.yi(y[2]),
.yi_1(y[1]),
.pij(pp2[2])
);
.x2i(x[2]),
.x2i_1(x[1]),
.yi(y[3]),

.yi_1(y[2]),
.pij(pp2[3])
);
.x2i(x[2]),
.x2i_1(x[1]),
.yi(y[4]),
.yi_1(y[3]),
.pij(pp2[4])
);
.x2i(x[2]),
.x2i_1(x[1]),
.yi(y[5]),
.yi_1(y[4]),
.pij(pp2[5])
);
.x2i(x[2]),
.x2i_1(x[1]),
.yi(y[6]),
.yi_1(y[5]),
.pij(pp2[6])
);
.x2i(x[2]),
.x2i_1(x[1]),
.yi(y[7]),
.yi_1(y[6]),
.pij(pp2[7])
);
//--------------------pp3---------------------------------//
// i=2 j=0;
.x2i(x[4]),
.x2i_1(x[3]),
.yi(y[0]),
.yi_1(1'b0),
.pij(pp3[0])
);
.x2i(x[4]),
.x2i_1(x[3]),
.yi(y[1]),
.yi_1(y[0]),
.pij(pp3[1])
);
.x2i(x[4]),
.x2i_1(x[3]),
.yi(y[2]),

.yi_1(y[1]),
.pij(pp3[2])
);
.x2i(x[4]),
.x2i_1(x[3]),
.yi(y[3]),
.yi_1(y[2]),
.pij(pp3[3])
);
.x2i(x[4]),
.x2i_1(x[3]),
.yi(y[4]),
.yi_1(y[3]),
.pij(pp3[4])
);
.x2i(x[4]),
.x2i_1(x[3]),
.yi(y[5]),
.yi_1(y[4]),
.pij(pp3[5])
);
.x2i(x[4]),
.x2i_1(x[3]),
.yi(y[6]),
.yi_1(y[5]),
.pij(pp3[6])
);
.x2i(x[4]),
.x2i_1(x[3]),
.yi(y[7]),
.yi_1(y[6]),
.pij(pp3[7])
);
//--- i=3 j=0 ------//
.x2i(x[6]),
.x2i_1(x[5]),
.yi(y[0]),

.yi_1(1'b0),
.pij(pp4[0])
);
.x2i(x[6]),
.x2i_1(x[5]),
.yi(y[1]),
.yi_1(y[0]),
.pij(pp4[1])
);
.x2i(x[6]),
.x2i_1(x[5]),
.yi(y[2]),
.yi_1(y[1]),
.pij(pp4[2])
);
.x2i(x[6]),
.x2i_1(x[5]),
.yi(y[3]),
.yi_1(y[2]),
.pij(pp4[3])
);
.x2i(x[6]),
.x2i_1(x[5]),
.yi(y[4]),
.yi_1(y[3]),
.pij(pp4[4])
);
.x2i(x[6]),
.x2i_1(x[5]),
.yi(y[5]),
.yi_1(y[4]),
.pij(pp4[5])
);
.x2i(x[6]),
.x2i_1(x[5]),
.yi(y[6]),
.yi_1(y[5]),
.pij(pp4[6])
);

.x2i(x[6]),
.x2i_1(x[5]),
.yi(y[7]),
.yi_1(y[6]),
.pij(pp4[7])
);
neggen u1 (
.x2i1(x[1]),.x2i(x[0]),.x2i_1(1'b0),.negi(neg[0])
);
neggen u2 (
.x2i1(x[3]),.x2i(x[2]),.x2i_1(x[1]),.negi(neg[1])
);
neggen u3 (
);
neggen u4 (
);
assign ppf1 = {5'd0,(~pp1[7]),pp1[7],pp1[7] ,pp1};
assign ppf2 = {4'd0,1'b1,(~pp2[7]),pp2,1'b0,neg[0]};
assign ppf3 = {2'd0,1'b1,(~pp3[7]),pp3,1'b0,neg[1],2'd0};
assign ppf4 = {1'b1,(~pp4[7]),pp4,1'd0,neg[2],4'd0};
assign const = {9'd0,neg[3],6'd0};
assign dout = ppf1+ppf2+ppf3+ppf4+const;
endmodule

1. CONCLUSION
In this brief, a simple approach has been proposed to generate a regular partial product array
with fewer partial product rows, thereby reducing the area, delay, and power of MBE multipliers. The
proposed approach has also been extended to regularize the partial product array of post truncated
MBE multipliers. Experimental results have demonstrated that the proposed MBE and post truncated
MBE multipliers with regular partial product arrays can achieve significant improvement in area, delay,
and powerconsumptionwhencomparedwithconventional multipliers.

References
[1][Maf01] Mafla, E. Course Notes, CDA3101, at URL http://www.cise.ufl.edu/~emafla/ (as-of
11 Apr 2001).
[2][Pat98] Patterson, D.A. and J.L. Hennesey. Computer Organization and Design: The
Hardware/Software Interface, Second Edition, San Francisco, CA: Morgan Kaufman (1998).
[3]. S. Wallace, “A suggestion for parallel multipliers,” IEEE Trans. Electron.Comput., vol. EC-
13, no. 1, pp. 14–17, Feb. 1964.
[4] O. Hasan and S. Kort, “Automated formal synthesis of Wallace tree multipliers,”in Proc.
50th Midwest Symp. Circuits Syst., 2007, pp. 293–296.
[5] J. Fadavi-Ardekani, “M × N booth encoded multiplier generator using optimized Wallace
trees,” IEEE Trans. Very Large Scale Integr. (VLSI) Syst., vol. 1, no. 2, pp. 120–125, Jun. 1993.
[6] F. Elguibaly, “A fast parallel multiplier-accumulator using the modified Booth algorithm,”
IEEE Trans. Circuits Syst. II, Analog Digit. Signal Process., vol. 47, no. 9, pp. 902–908, Sep.
2000.
[7] K. Choi and M. Song, “Design of a high performance 32 × 32-bit multiplier with a novel sign
select Booth encoder,” in Proc. IEEE Int. Symp. Circuits Syst., 2001, vol. 2, pp. 701–704.
[8] Y. E. Kim, J. O. Yoon, K. J. Cho, J. G. Chung, S. I. Cho, and S. S. Choi, “Efficient design of
modified Booth multipliers for predetermined coefficients,” in Proc. IEEE Int. Symp. Circuits
Syst., 2006, pp. 2717–2720.
[9] W.-C. Yeh and C.-W. Jen, “High-speed booth encoded parallel multiplier design,” IEEE
Trans. Comput., vol. 49, no. 7, pp. 692–701, Jul. 2000.
[10] J.-Y. Kang and J.-L. Gaudiot, “A simple high-speed multiplier design,” IEEE Trans.
Comput., vol. 55, no. 10, pp. 1253–1258, Oct. 2006.

Modified booth

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Similar to Modified booth

Similar to Modified booth (20)

Recently uploaded

Recently uploaded (20)

Modified booth