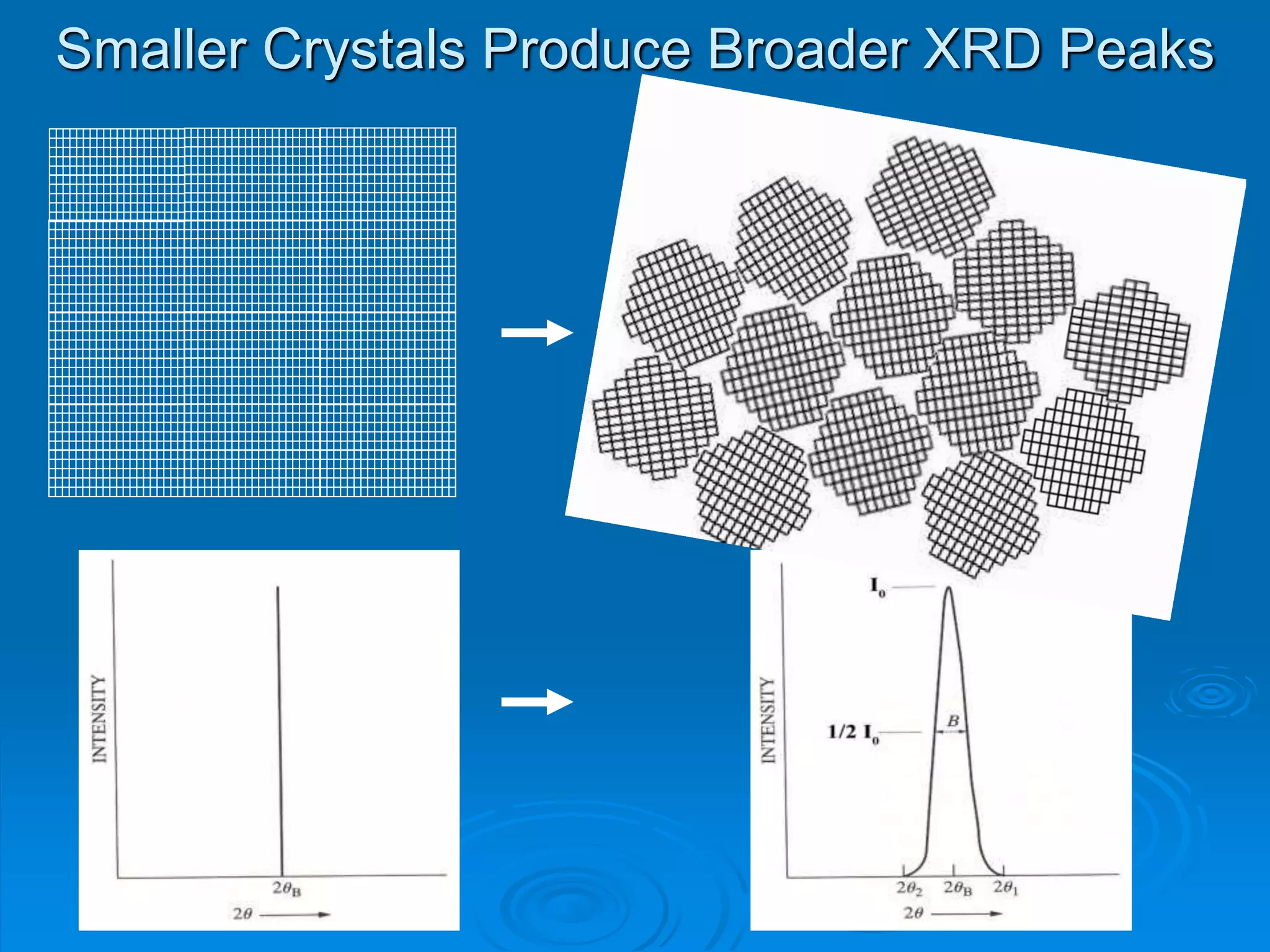
This document discusses the basics of X-ray diffraction, including Bragg's law, lattice constants, Laue conditions, and θ-2θ scans. It provides examples of using Bragg's law to calculate interplanar spacing and using Scherrer's formula to determine crystallite size from peak broadening in an XRD pattern of gold foil.

1. X-ray Diffraction
The Basics
Followed by a few examples of
Data Analysis
by
Wesley Tennyson
NanoLab/NSF NUE/Bumm

2. NanoLab/NSF NUE/Bumm
X-ray Diffraction
Bragg’s Law
Lattice Constants
Laue Conditions
θ - 2θ Scan
Scherrer’s Formula
Data Analysis Examples

3. Bragg’s Law
nλ = 2 d sin θ
• Constructive interference only occurs for certain θ’s
correlating to a (hkl) plane, specifically when the path
difference is equal to n wavelengths.

4. NanoLab/NSF NUE/Bumm
Bragg condition’s
The diffraction condition can be written in vector
form
2k∙G + G2 = 0
k - is the incident wave vector
k’ - is the reflected wave vector
G - is a reciprocal lattice vector such that where
G = ∆k = k - k’
the diffraction condition is met

5. NanoLab/NSF NUE/Bumm
Lattice Constants
The distance between planes of atoms is
d(hkl) = 2π / |G|
Since G can be written as
G = 2π/a (h*b1+ k*b2 +l*b3)
Substitute in G
d(hkl) = a / (h2 + k2 + l2)(1/2)
Or
a = d * (h2 + k2 + l2)(1/2)
a is the spacing between nearest neighbors

6. NanoLab/NSF NUE/Bumm
Laue Conditions
a1∙∆k = 2πυ1 a2∙∆k = 2πυ2
a3∙∆k = 2πυ3
Each of the above describes a cone in reciprocal
space about the lattice vectors a1, a2, and a3.
 the υi are integers
When a reciprocal lattice point intersects this cone the
diffraction condition is met, this is generally called
the Ewald sphere.

7. NanoLab/NSF NUE/Bumm
Summary of Bragg & Laue
When a diffraction
condition is met there can
be a reflected X-ray
 Extra atoms in the basis can
suppress reflections
Three variables λ, θ, and d
 λ is known
 θ is measured in the
experiment (2θ)
 d is calculated
From the planes (hkl)
 a is calculated


sin
2
n
d 
2
2
2
l
k
h
d
a 



8. NanoLab/NSF NUE/Bumm
θ - 2θ Scan
The θ - 2θ scan maintains these angles with the
sample, detector and X-ray source
Normal to surface
Only planes of atoms that share this normal will be seen in the θ - 2θ Scan

9. NanoLab/NSF NUE/Bumm
θ - 2θ Scan
The incident X-rays may reflect in many directions
but will only be measured at one location so we
will require that:
Angle of incidence (θi) = Angle of reflection (θr)
This is done by moving the detector twice as fast
in θ as the source. So, only where θi = θr is the
intensity of the reflect wave (counts of photons)
measured.

10. NanoLab/NSF NUE/Bumm
θ - 2θ Scan

11. Smaller Crystals Produce Broader XRD Peaks

12. t = thickness of crystallite
K = constant dependent on crystallite shape (0.89)
 = x-ray wavelength
B = FWHM (full width at half max) or integral breadth
B = Bragg Angle
Scherrer’s Formula
B
cos
B
K
t






13. Scherrer’s Formula
What is B?
B = (2θ High) – (2θ Low)
B is the difference in
angles at half max
2θ high
Noise
2θ low
Peak

14. When to Use Scherrer’s Formula
 Crystallite size <1000 Å
 Peak broadening by other factors
 Causes of broadening
• Size
• Strain
• Instrument
 If breadth consistent for each peak then assured
broadening due to crystallite size
 K depends on definition of t and B
 Within 20%-30% accuracy at best
Sherrer’s Formula References
Corman, D. Scherrer’s Formula: Using XRD to Determine Average Diameter of
Nanocrystals.

15. Data Analysis
 Plot the data (2θ vs. Counts)
 Determine the Bragg Angles for the peaks
 Calculate d and a for each peak
 Apply Scherrer’s Formula to the peaks

16. Bragg Example

17. Bragg Example
d = λ / (2 Sin θB) λ = 1.54 Ǻ
= 1.54 Ǻ / ( 2 * Sin ( 38.3 / 2 ) )
= 2.35 Ǻ
Simple Right!

18. Scherrer’s Example
Au Foil
98.25 (400)
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
95 95.5 96 96.5 97 97.5 98 98.5 99 99.5 100 100.5 101 101.5 102
2 Theta
Counts

19. Scherrer’s Example
B
B
t


cos
89
.
0



t = 0.89*λ / (B Cos θB) λ = 1.54 Ǻ
= 0.89*1.54 Ǻ / ( 0.00174 * Cos (98.25/ 2 ) )
= 1200 Ǻ
B = (98.3 - 98.2)*π/180 = 0.00174
Simple Right!