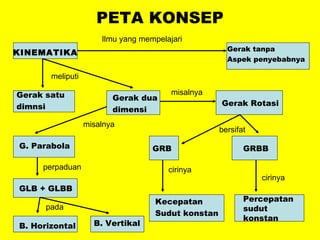
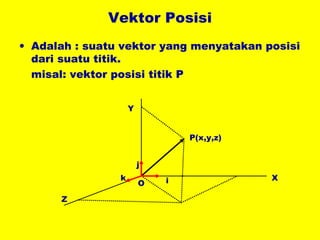
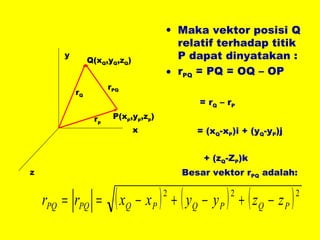
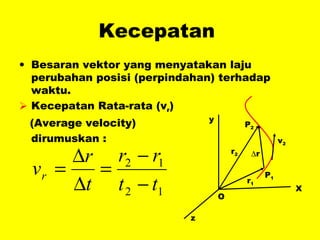
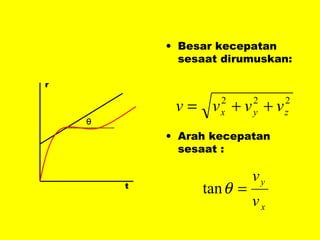
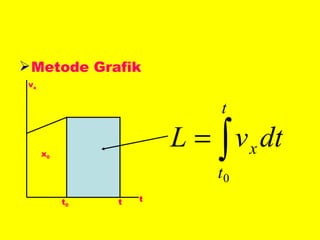
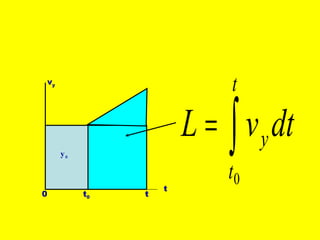
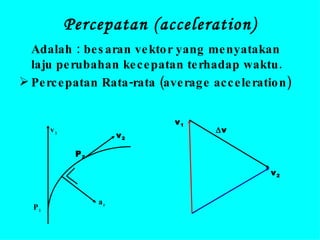
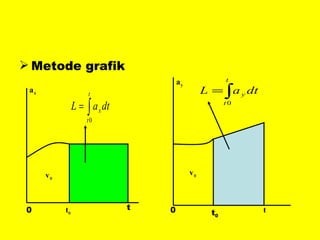
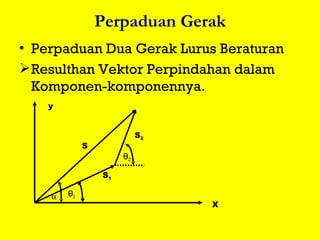
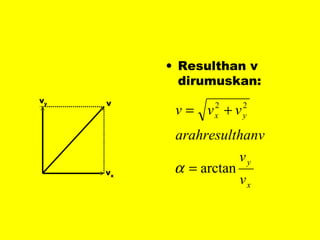
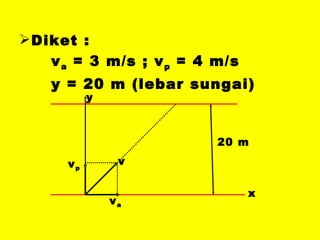
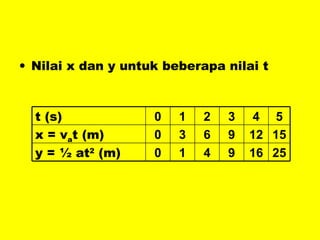
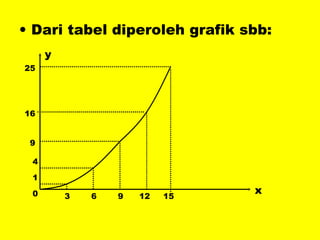
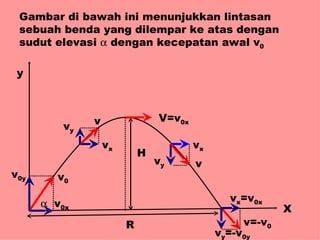
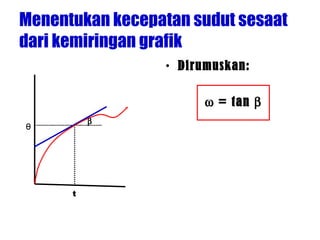
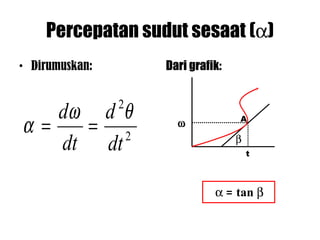
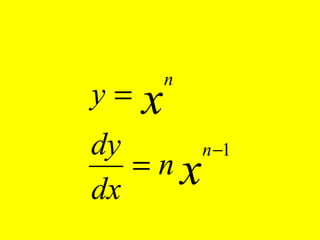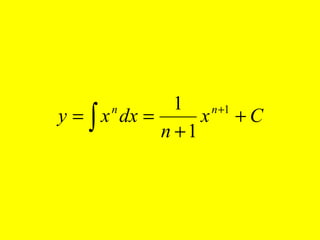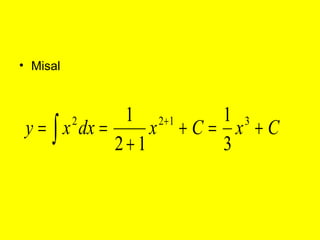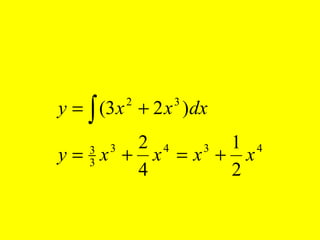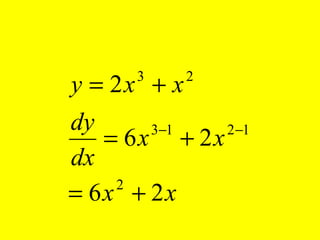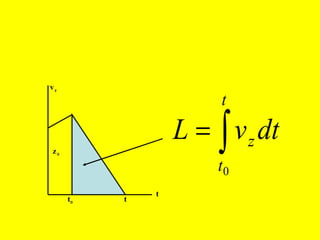Dokumen ini menguraikan standar kompetensi dan kompetensi dasar fisika kelas XI, termasuk analisis gerakan dan penerapan hukum fisika. Pembahasan mencakup kinematika, gerak lurus dan melingkar, serta hukum kekekalan energi mekanik. Siswa diharapkan mampu menganalisis berbagai jenis gerak dan menerapkan konsep vektor dalam permasalahan fisika sehari-hari.

1. STANDAR KOMPETENSI DAN KOMPETENSI DASAR FISIKA KELAS XI SEMESTER 1

2. STANDAR KOMPETENSI KOMPETENSI DASAR Menganalisis gejala alam dan keteraturannya dalam cakupan mekanik benda titik Menganalisis gerak lurus, gerak melingkar, gerak parabola dengan menggunakan vektor. Menganalisis keteraturan gerak planet dalam tatasurya berdasarkan hukum-hukum Newton. Menganalisis pengaruh gaya pada sifat elastisitas bahan. Menganalisis hubungan antara gaya dengan gerak getaran. Menganalisis hubungan antara usaha, perubahan energi dengan dengan hukum kekekala energi mekanik. Menerapkan hukum kekekalan energi mekanik untuk menganalisis gerak dalam kehidupan sehari-hari. Menunjukkan hubungan antara konsep impuls dan momentum untuk menyelesaikan masalah tumbukan.

3. Bab I Kinematika dengan Analisis Vektor Tujuan : Setelah mempelajari bab ini siswa diharapkan mampu: Menganalisis gerak tanpa dan gerak dengan percepatan tetap. Menentukan hubungan grafik x – t, v – t, dan a – t Menganalisis besaran perpindahan, kecepatan, dan percepatan pada perpaduan gerak lurus dengan menggunakan vektor. Menganalisis besaran perpindahan dan kecepatan pada gerak parabola dengan menggunakan vektor. Menganalisis besaran perpindahan dan kecepatan pada gerak melingkar dengan menggunakan vektor. Menentukan persamaan fungsi sudut, kecepatan sudut, dan percepatan sudut pada gerak melingkar. Menganalisis vektor percepatan tangensial dan percepatan sentripetal pada gerak melingkar.

4. PETA KONSEP KINEMATIKA Gerak tanpa Aspek penyebabnya Gerak satu dimnsi Gerak dua dimensi Gerak Rotasi GRB GRBB G. Parabola GLB + GLBB B. Horizontal B. Vertikal Kecepatan Sudut konstan Percepatan sudut konstan Ilmu yang mempelajari meliputi misalnya misalnya perpaduan pada bersifat cirinya cirinya

6. Misal :

8. Misal

11. Persamaan Gerak Vektor satuan adalah suatu vektor yang besarnya satu satuan. X Y Z i j k

12. Vektor Posisi Adalah : suatu vektor yang menyatakan posisi dari suatu titik. misal: vektor posisi titik P X Y Z i j k P(x,y,z) O

13. Maka vektor posisi titik P relatif terhadap pusat koordinat didefinisikan sebagai : r = OP =x i + y j +z k dan besarnya vektor r :

14. Maka vektor posisi Q relatif terhadap titik P dapat dinyatakan : r PQ = PQ = OQ – OP = r Q – r P = (x Q -x P )i + (y Q -y P )j + (z Q -Z P )k Besar vektor r PQ adalah: x y z r p r Q r PQ P(x p ,y p ,z p ) Q(x Q ,y Q ,z Q )

15. Contoh Vektor posisi suatu benda diberikan oleh r = (t 3 - 2t 2 )i + (3t 2 )j; t dalam sekon dan r dalam meter. Tentukan besar dan arah perpindahan benda dari t = 2 s sampai t = 3 s.

16. Penyelesaian untuk t 1 = 2 s r 1 = (2 3 – 2 x 2 2 ) i + (3 x 2 2 ) j = 12 j untuk t 2 = 3 s r 2 = (3 3 – 2 x 3 2 ) i + (3 x 3 2 ) j = 9i + 27j maka vektor perpindahannya adalah:  r = r 2 – r 1 = (9i + 27j) – (12j) = 9i + 15j sehingga besar perpindahannya:  r =  x 2 +  y 2 =  9 2 + 15 2 = 3  34 m arah perpindahan: tan θ =  y/  x = 15/9 = 5/3 θ = arc tan (5/3) = 59 o

17. Kecepatan Besaran vektor yang menyatakan laju perubahan posisi (perpindahan) terhadap waktu. Kecepatan Rata-rata (v r ) (Average velocity) dirumuskan : X y z O r 1 r 2 P 1 P 2 v 2  r

18. Apabila dinyatakan dalam vektor satuan :

19. Kecepatan Sesaat (Instantaneous velocity). yaitu : limit kecepatan rata-rata ketika interval waktunya mendekati nol.

20. Besar kecepatan sesaat dirumuskan: Arah kecepatan sesaat : r t θ

21. Uji kemampuan Posisi sebuah partikel diberikan oleh r(t) = x(t)i + y(t)j, dengan x(t) = 2t + 1 dan y(t) = 4t 2 + 2 untuk r, x, dan y dalam meter, t dalam sekon, dan konstanta dalam satuan yang sesuai. Tentukan vektor posisi dan jarak partikel dari titik asal pada saat t = 2 sekon. Tentukan perpindahan dan kecepatan rata-rata partikel dalam selang waktu t = 2 sekon hingga t = 5 sekon. Tentukan persamaan umum kecepatan partikel. Tentukan kelajuan partikel pada t = 2 sekon.

22. Menentukan posisi dari kecepatan: Metode Integral Atau :

23. Secara umum, posisi benda dalam lintasannya dapat dirumuskan:

24. Metode Grafik v x t x 0 t 0 t

25. v y t 0 t 0 t y 0

26. v z z 0 t t 0 t

27. Uji Kemampuan Persamaan kecepatan partikel sebagai fungsi waktu dinyatakan oleh v = 4t 2 i – 3tj +2k. Jika posisi partikel mula-mula berada pada pusat koordinat, tentukanlah posisi partikel sebagai fungsi waktu.

28. Percepatan (acceleration) Adalah : besaran vektor yang menyatakan laju perubahan kecepatan terhadap waktu. Percepatan Rata-rata (average acceleration) v 1 v 2 a r P 2 P 1 v 1 v 2  v

29. Secara metematis percepatan rata-rata dirumuskan :

30. Jika dinyatakan dalam vektor satuan:

31. Percepatan sesaat (instantaneous acceleration) Adalah limit percepatan rata-rata ketika interval waktunya mendekati nol.

32. Percepatan sebagai turunan ke dua dari vektor posisi: Dirumuskan : Sehingga vektor percepatan a menjadi :

33. Besar vektor percepatan dirumuskan : v t O P 

34. Menentukan Kecepatan dari fungsi Percepatan: Metode Integral

35. Dalam komponen-komponen x, y, dan z: Secara umum dirumuskan :

36. Metode grafik a x 0 t 0 t v 0 a y 0 v 0 t 0 t

37. Secara vektor S dapat dinyatakan: S = S 1 + S 2 Pada sumbu X : S x = S 1x + S 2x S x = S 1 cos θ 1 + S 2 cos θ 2 Pada sumbu y : S y = S 1y + S 2y S y = S 1 sin θ 1 + S 2 sin θ 2

38. Perpaduan Gerak Perpaduan Dua Gerak Lurus Beraturan Resulthan Vektor Perpindahan dalam Komponen-komponennya. S 1 S 2 S X y θ 1  θ 2

39. Sehingga besar vektor resulthan S dapat dirumuskan: Sedangka arah S terhadap sumbu X adalah :

40. Cara yang lebih sederhana :

41. Perpaduan Dua Gerak Lurus Beraturan yang Saling tagak Lurus Resulthan S dirumuskan : S S y S x 

42. Resulthan v dirumuskan: v v y v x

43. Ilustrasi Sebuah perahu akan menyeberangi sungai secara tegak lurus terhadap aliran sungai. Kapan dan dimana perahu tersebut sampai di seberang sungai, jika lebar sungai 20 m, kecepatan perahu terhadap aliran sungai 4 m/s, dan kecepatan aliran sungai 3 m/s relatif terhadap tepi sungai.

44. Diket : v a = 3 m/s ; v p = 4 m/s y = 20 m (lebar sungai) v v p v a x y 20 m

45. Ditanya : x dan t y Jawab : nilai x dan y untuk beberapa nilai t t (s) 0 1 2 3 4 5 X =v a t (m) 0 3 6 9 12 15 Y =v p t (m) 0 4 8 12 16 20

46. Grafik lintasan perpaduan dua GLB pada bidang xy. x y 0 3 6 9 12 15 4 8 12 16 20

47. Dari grafik dapat disimpulkan bahwa perpaduan antara GLB dengan GLB akan menghasilkan GLB juga. Waktu yang dibutuhkan perahu sampai seberang sungai:

48. Posisi perahu setelah di seberang sungai:

49. Uji Kemampuanmu Rek! Sebuah perahu bergerak dengan kecepatan 0,3 m/s arah ke Barat laut relatif terhadap tepi sungai. Perahu tersebut berada di sungai yang airnya mengalir dengan kecepatan 0,5 m/s arah ke Barat relatif terhadap tepi sungai. Tentukan besar dan arah kecepatan perahu relatif terhadap aliran sungai.

50. Seorang pilot berusaha menerbangkan pesawatnya ke Utara. Tiba-tiba ada angin berhembus dengan kecepatan 80 km/jam ke Barat. Jika kelajuan pesawat terbang di udara 240 km/jam, ke mana pesawat harus di arahkan?

51. Perpaduan GLB dengan GLBB Gerak dalam Bidang Horizontal Masih ingat dengan perahu yang menyeberangi sungai? Sekarang perahu menyeberangi sungai dengan GLBB tanpa kecepatan awal tetapi mempunyai percepatan 2 m/s 2 . Kalau begitu bagaimana bentuk grafiknya?

52. Nilai x dan y untuk beberapa nilai t t (s) 0 1 2 3 4 5 x = v a t (m) 0 3 6 9 12 15 y = ½ at 2 (m) 0 1 4 9 16 25

53. Dari tabel diperoleh grafik sbb: x y 0 3 6 9 12 15 1 4 9 16 25

54. Dari grafik dapat disimpulkan : “ Perpaduan antara GLB dengan GLBB akan menghasilkan gerak parabola”

55. Gerak dalam Bidang Vertikal. Perpaduan antara GLB arah Horizontal dengan GLBB arah vertikal dengan besar percepatan a = g yang secara umum disebut gerak peluru .

56. Gambar di bawah ini menunjukkan lintasan sebuah benda yang dilempar ke atas dengan sudut elevasi  dengan kecepatan awal v 0 X H R y  v 0 v 0x v 0y v v x v y V=v 0x v v x v y v x =v 0x v y =-v 0y v=-v 0

57. Komponen vektor kecepatan awal (v o ) Pada sumbu X : v ox = v o cos  Pada sumbu y : v oy = v o sin  Kecepatan benda setiap saat (v) Pada sumbu x (GLB) : v x = v ox = v o cos  Pada sumbu y (GLBB) : v y = v oy – gt = v o sin  - gt

58. maka : arah v terhadap sumbu x :

59. Posisi benda setiap saat Pada sumbu x (GLB): x = v ox t = (v o cos  )t Pada sumbu y (GLBB): y = v oy t -½gt 2 = (v o sin  )t - ½gt 2 Besar perpindahan:

60. Arah perpindahan terhadap sumbu x

61. Ketinggian maksimum (H) kecepatan di ketinggian maksimum pada sumbu y adalah: v y = 0 V o sin  - gt = 0 V o sin  = gt

62. Koordinat x dari titik tertinggi H

63. Jika t H di masukkan ke dalam persamaan: y = H =(v o sin  )t H - ½gt H didapat ketinggin maksimum H: Koordinat y dari titik tertinggi H

64. Jika t H di masukkan ke dalam persamaan: y = H =(v o sin  )t H - ½gt H didapat ketinggin maksimum H: Koordinat y dari titik tertinggi H

65. Jarak terjauh (R) Berdasar sifat sumbu simetri: waktu naik = waktu turun pada ketinggian yang sama maka besar kecepatan naik = besar kecepatan turun tetapi arah kecepatan berbeda. sehingga R dirumuskan :

66. PERSAMAAN FUNGSI POSISI SUDUT, KECEPATAN SUDUT, DAN PERCEPATAN SUDUT Posisi Sudut( θ ) Persamaan fungsi posisi sudut θ terhadap waktu t secara umum di rumuskan : θ (t) = a + bt + ct 2 +…+ zt n dimana: a,b,c,…z : konstanta 1,2,3,…n : eksponen

67. Perpindahan posisi sudut dirumuskan:  θ = θ 2 – θ 1 Kecepatan sudut rata-rata (  r ) dirumuskan: Kecepatan sudut sesaat (  ) dirumuskan:

68. Menentukan kecepatan sudut sesaat dari kemiringan grafik Dirumuskan:  = tan  t θ 

69. Menentukan Posisi sudut dari fungsi kecepatan sudut sesaat

70. Percepatan Sudut Percepatan sudut rata-rata (  r ) dirumuskan:

71. Percepatan sudut sesaat (  ) Dirumuskan: Dari grafik:  = tan  t  A 

72. Menentukan Kecepatan Sudut dari Fungsi percepatan sudut sesaat