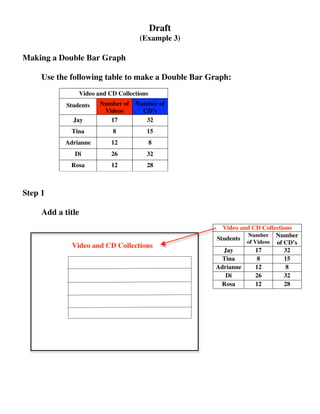
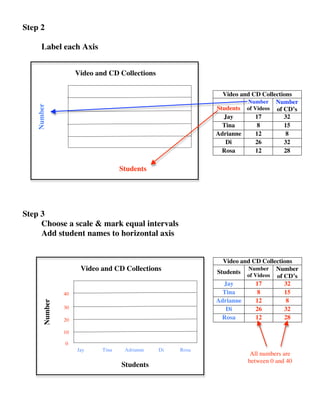
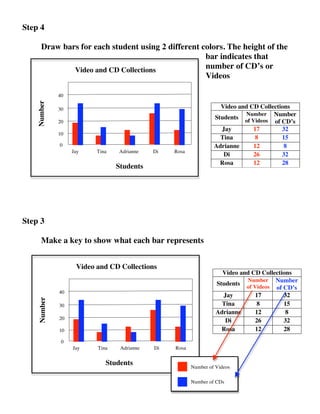
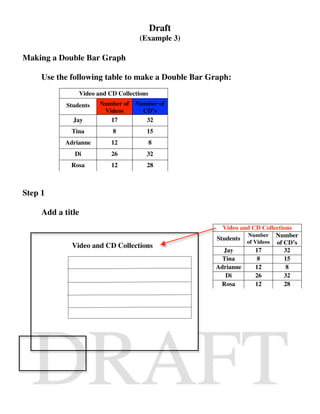
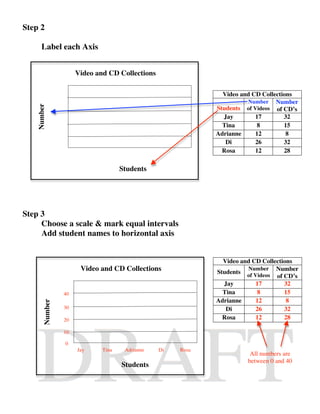
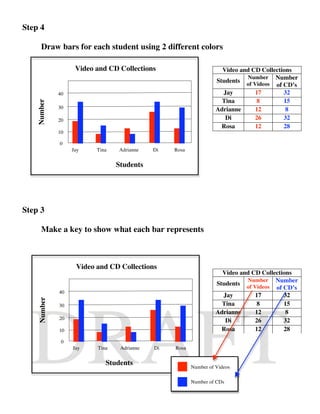
The document provides details about three worked examples that are intended to teach students various math and data skills. Worked Example 1 shows how to add mixed numbers with unlike denominators through step-by-step instructions. Worked Example 2 demonstrates solving basic equations with one variable using addition and subtraction. Worked Example 3 outlines the process for students to create a double bar graph from a provided data table. The examples are intended for students ages 8-13 and aim to address specific learning goals and gaps through interactive instructional modules.

1. Worked Examples Project
Jennifer Kaupke
October 7, 2012
EDT 503

2. Worked Example 1
Addition of Mixed Numbers
http://www.eduplace.com/
Scope of Worked Example 1
• Audience:
o Age: 10‐11
o Gender: male or female
o Reading level: beginning reading level
o Motivation: Knowing how to add mixed numbers with unlike denominators
• Prerequisites for Project: Student must have prior knowledge in finding equivalent fractions,
addition and subtraction of fractions, and finding multiples.
• Learning Module Goal:
o Objectives: Student will add mixed numbers with unlike denominators
o Givens: Mixed numbers with unlike denominators
o Type of task, transfer context, assessment: N/A
• How module addresses learner motivation: N/A
• Performance gap addressed by the module: N/A
Instructional Media Choices:
• Learning Module’s Content: This example provides mixed numbers that must be added. The
module also shows, at the end of the problem, that depending on the common denominator
chosen, the student may have to change their solution from a mixed number containing an
improper fraction to a proper mixed number.
• Instructional Context: N/A
• How the content is best delivered: N/A
• How the audience will interact with the module: N/A
• How the learning module is designed to manage cognitive load: In the original example there is a
presence of split‐attention because the student must split their attention between the paragraphs
of directions/explanations and the worked examples. In the draft example, I separated the addition
of mixed numbers into more basic steps and eliminated lengthy descriptions. This will provide a
clearer understanding by the student as they move through the example. I also chose to use the
LCM rather than another common multiple because it eliminates the need for simplifying the
fraction.

3. Original
(Example 1)

4. Draft
(Example 1)
Adding Mixed Numbers
Solve:
4
+ 2
Step 1
Find the Least Common Multiple of the two denominators
6: 6, 12, 18, 24, 30, 36, 42, 48
8: 8, 16, 24, 32, 40, 48, 56, 64
Step 2
Use the Least Common Multiple to find equivalent fractions:
4 x = 4
+ 2 x = 2
Step 3
Add the whole numbers
4 x = 4
+ 2 x = 2
6

5. Step 4
Add the Fractions
4 x = 4
+ 2 x = 2 If this fraction is improper
(larger numerator than
denominator), continue to
6 step 5
Step 5
Convert Improper Fraction to Mixed Number
Check to see how many times
4 x = 4 the denominator will go into the
numerator; this is your whole
+ 2 x = 2 number. The remainder is the
new numerator.
6 = 1
Step 6
Combine Whole Number with Mixed Number
4 x = 4
+ 2 x = 2
6 + 1
7 Final solution

6. Worked Example 2
Equations with One Variable
http://www.eduplace.com/
Scope of Worked Example 2
• Audience:
o Age: 8‐11
o Gender: male or female
o Reading level: beginning reading level
o Motivation: Knowing how solve basic equations with one variable
• Prerequisites for Project: Student must have prior knowledge in the addition and subtraction,
inverse operations and the zero property of addition.
• Learning Module Goal:
o Objectives: Student will solve basic equations with one variable for addition and subtraction
o Givens: Equations containing addition and subtraction with one variable
o Type of task: N/A
o Transfer context: N/A
o Assessment: N/A
• How module addresses learner motivation: N/A
• Performance gap addressed by the module: N/A
Instructional Media Choices:
• Learning Module’s Content: This example provides the student with two examples of simple
equations that could be solved through a “guess‐and‐check” strategy. There is a sample with
addition and one with subtraction. Definitions are also provided for: arithmetic expression,
algebraic expression and variable.
• Instructional Context: N/A
• How the content is best delivered: N/A
• How the audience will interact with the module: N/A
• How the learning module is designed to manage cognitive load: In the original example there is a
presence of split‐attention because the student must split their attention between the paragraphs
of definitions/explanations and the worked examples. The definitions presented are not particularly
relevant to the problems presented and would most likely add confusion. In the draft example, I
included the definitions with visuals, showed the equations being solved as a step‐by‐step process
and highlighted numbers where students would need to focus their attention.

7. Original
(Example 2)
Expressions and Equations
An arithmetic expression consists of numbers and operations using parentheses,
exponents, multiplication, division, addition, and subtraction. An algebraic expression is
like an arithmetic expression, but contains at least one variable. A variable is a letter that
represents a number. The equality of two expressions gives an equation. To solve an
equation means to find the value of the variable that will make the equation true.
Examples:
p + 4 = 11 x−3=9
p = 11 − 4 ← Use inverse operations. → x=9+3
p=7 x = 12

8. Draft
(Example 2)
Solving Simple Equations
Solve for p:
p + 4 = 11
Step 1
Identify the variable
p + 4 = 11
A variable is a letter or
symbol that stands for a
number
Step 2
Isolate the variable by using the inverse operation on both
sides of the equal sign
p + 4 = 11
- 4 -4
p + 0 = 7
Step 4
Applying the Zero Property of Addition, notice that the + 0
in the problem can be removed and you have solved for your variable.
p + 0 = 7
p = 7

9. Solving Simple Equations
Solve for x:
x - 3= 9
Step 1
Identify the variable
x - 3= 9
A variable is a letter or
symbol that stands for a
number
Step 2
Isolate the variable by using the inverse operation on both
sides of the equal sign
x - 3 = 9
+ 3 +3
x + 0 = 12
Step 4
Applying the Zero Property of Addition, notice that the + 0
in the problem can be removed and you have solved for your variable.
x + 0 = 12
x = 12

10. Worked Example 3
Making a Double Bar Graph
http://www.eduplace.com/
Scope of Worked Example 3
• Audience:
o Age: 9‐13
o Gender: male or female
o Reading level: beginning reading level
o Motivation: Knowing how to create a double bar graph
• Prerequisites for Project: Student must have prior knowledge in reading tables.
• Learning Module Goal:
o Objectives: Students will create a double bar graph using the provided table of data.
o Type of task: N/A
o Transfer context: N/A
o Assessment: N/A
• How module addresses learner motivation: N/A
• Performance gap addressed by the module: N/A
Instructional Media Choices:
• Learning Module’s Content: This example provides the student with the steps required to create a
double bar graph with a provided table of data. It also includes a finished double bar graph.
• Instructional Context: N/A
• How the content is best delivered: N/A
• How the audience will interact with the module: N/A
• How the learning module is designed to manage cognitive load: In the original example there is a
presence of split‐attention because the student must split their attention between table, the
introduction paragraphs, the steps listed, and the double bar graph provided. In the draft example, I
included the definitions with visuals, showed the equations being solved as a step‐by‐step process
and highlighted numbers where students would need to focus their attention. Presenting the
information in this manner will allow students to see each step as they move through the creation
of their double bar graph rather than only seeing the finished product and trying to decipher which
steps relates to each part of the finished product.

11. Original
(Example 3)

12. Draft
(Example 3)
Making a Double Bar Graph
Use the following table to make a Double Bar Graph:
Video and CD Collections
Students Number of Number of
Videos CD’s
Jay 17 32
Tina 8 15
Adrianne 12 8
Di 26 32
Rosa 12 28
Step 1
Add a title
Video and CD Collections
Number Number
Students
of Videos of CD’s
Video and CD Collections
Jay 17 32
Tina 8 15
Adrianne 12 8
Di 26 32
Rosa 12 28

13. Step 2
Label each Axis
Video and CD Collections
Video and CD Collections
Number Number
Number
Students of Videos of CD’s
Jay 17 32
Tina 8 15
Adrianne 12 8
Di 26 32
Rosa 12 28
Students
Step 3
Choose a scale & mark equal intervals
Add student names to horizontal axis
Video and CD Collections
Video and CD Collections Students of Videos Number
Number
of CD’s
Jay 17 32
40 Tina 8 15
Adrianne 12 8
Number
30 Di 26 32
20 Rosa 12 28
10
0
Jay Tina Adrianne Di Rosa
All numbers are
between 0 and 40
Students

14. Step 4
Draw bars for each student using 2 different colors. The height of the
bar indicates that
Video and CD Collections
number of CD’s or
Videos
40
Number
30 Video and CD Collections
Students of Videos Number
Number
20 of CD’s
Jay 17 32
10
Tina 8 15
0 Adrianne 12 8
Jay Tina Adrianne Di Rosa
Di 26 32
Rosa 12 28
Students
Step 3
Make a key to show what each bar represents
Video and CD Collections
Video and CD Collections
Students of Videos Number
Number
of CD’s
40
Jay 17 32
Number
30 Tina 8 15
Adrianne 12 8
20 Di 26 32
10 Rosa 12 28
0
Jay Tina Adrianne Di Rosa
Students Number of Videos
Number of CDs

15. Peer Review 1
EDT 503: Integrated Worked Examples Project
Student Name: Jennifer Kaupke, reviewed by Emily Schwartz
Requirements Final Submission:
Are the following items included with submission?
Yes No
Project Draft
Copy of peer comments
Final, revised version of project
A revised version of your design document
Scoring Rubric:
Points Points
Category Possible Awarded Comments
The examples are appropriate 5 5
Elements are properly aligned 5 5
Good use of contrast 5 5
Similar elements are in close proximity 5 5
Similar elements are repeated 5 5
Instructions are error free (spelling, grammar) 5 5
Design is well justified in the design document 5 5
and it adheres to the template provided in class
Limited or no extraneous/distracting content 5 5
Point Total 40 40
General Comment:
Hi Jennifer. This looks great! I’m wondering- in your first example, is there a way to further connect
step 1 back to the problem? In case a student didn’t understand where the 6 and the 8 came from?
Other than that I thought your examples were very clear and easy to follow.

16. Peer Review 2
EDT 503: Integrated Worked Examples Project
Student Name: Anna Lisa Bussell reviewing Jennifer Kaupke
Requirements Final Submission:
Are the following items included with submission?
Yes No
Project Draft
Copy of peer comments
Final, revised version of project
A revised version of your design document
Scoring Rubric:
Points Points
Category Possible Awarded Comments
The examples are appropriate 5 5 Very detailed and well explained
Elements are properly aligned 5 4 Example 3, Step 1 has an empty
text box.
Good use of contrast 5 5
Similar elements are in close proximity 5 5
Similar elements are repeated 5 5
Instructions are error free (spelling, grammar) 5 5
Design is well justified in the design document 5 5
and it adheres to the template provided in class
Limited or no extraneous/distracting content 5 4 Example 3, Step 2, maybe a
different use of the arrows?
Point Total 40 38
General Comment:

17. Peer Review 3
EDT 503: Integrated Worked Examples Project
Student Name: For Jennifer Kaupke (Reviewed by Amy Tregre)
Requirements Final Submission:
Are the following items included with submission?
Yes No
Project Draft
Copy of peer comments
Final, revised version of project
A revised version of your design document
Scoring Rubric:
Points Points
Category Possible Awarded Comments
The examples are appropriate 5 5
Elements are properly aligned 5 5
Good use of contrast 5 5
Similar elements are in close proximity 5 5
Similar elements are repeated 5 5
Instructions are error free (spelling, 5 5
grammar)
Design is well justified in the design 5 5
document and it adheres to the template
provided in class
Limited or no extraneous/distracting 5 5
content
Point Total 40 40 See notes below
General Comment:
Jennifer,
These were great examples with good use of color and sequencing!
#1:
Step 4: define “improper fraction”?
Step 5: show process?
Step 6: I like the circles ;) Maybe write “answer” or “solution” next to final fraction?
#2
Good consistency, color usage, and sequencing. Steps and solution are clear. Key
vocabulary enhances understanding.
#3
Very clear! Great use of color, arrows, and consistency in representing the chart in
relation to the bar graph. Clear progression; would be easy to follow!
Typos:
Objectives: Fragment
Learner Module’s Content: “This example provides the student with the steps
required…i ”

18. Worked Example 1
Addition of Mixed Numbers
http://www.eduplace.com/
Scope of Worked Example 1
• Audience:
o Age: 10‐11
o Gender: male or female
o Reading level: beginning reading level
o Motivation: Knowing how to add mixed numbers with unlike denominators
• Prerequisites for Project: Student must have prior knowledge in finding equivalent fractions,
addition and subtraction of fractions, and finding multiples.
• Learning Module Goal:
o Objectives: Student will add mixed numbers with unlike denominators
o Givens: Mixed numbers with unlike denominators
o Type of task, transfer context, assessment: N/A
• How module addresses learner motivation: N/A
• Performance gap addressed by the module: N/A
Instructional Media Choices:
• Learning Module’s Content: This example provides mixed numbers that must be added. The
module also shows, at the end of the problem, that depending on the common denominator
chosen, the student may have to change their solution from a mixed number containing an
improper fraction to a proper mixed number.
• Instructional Context: N/A
• How the content is best delivered: N/A
• How the audience will interact with the module: N/A
• How the learning module is designed to manage cognitive load: In the original example there is a
presence of split‐attention because the student must split their attention between the paragraphs
of directions/explanations and the worked examples. In the draft example, I separated the addition
of mixed numbers into more basic steps and eliminated lengthy descriptions. This will provide a
clearer understanding by the student as they move through the example. I also chose to use the
LCM rather than another common multiple because it eliminates the need for simplifying the
fraction.

19. Original
(Example 1)

20. Draft
(Example 1)
Adding Mixed Numbers
Solve:
4
+ 2
Step 1
Find the Least Common Multiple
6: 6, 12, 18, 24, 30, 36, 42, 48
8: 8, 16, 24, 32, 40, 48, 56, 64
Step 2
Use the Least Common Multiple to find equivalent fractions:
4 x = 4
+ 2 x = 2
Step 3
Add the whole numbers
4 x = 4
+ 2 x = 2
6

21. Step 4
Add the Fractions
4 x = 4
+ 2 x = 2
If this fraction is improper,
6 continue to step 5
Step 5
Convert Improper Fraction to Mixed Number
4 x = 4
+ 2 x = 2
6 = 1
Step 6
Combine Whole Number with Mixed Number
4 x = 4
+ 2 x = 2
6 + 1
7

22. Worked Example 2
Equations with One Variable
http://www.eduplace.com/
Scope of Worked Example 2
• Audience:
o Age: 8‐11
o Gender: male or female
o Reading level: beginning reading level
o Motivation: Knowing how solve basic equations with one variable
• Prerequisites for Project: Student must have prior knowledge in the addition and subtraction,
inverse operations and the zero property of addition.
• Learning Module Goal:
o Objectives: Student will solve basic equations with one variable for addition and subtraction
o Givens: Equations containing addition and subtraction with one variable
o Type of task: N/A
o Transfer context: N/A
o Assessment: N/A
• How module addresses learner motivation: N/A
• Performance gap addressed by the module: N/A
Instructional Media Choices:
• Learning Module’s Content: This example provides the student with two examples of simple
equations that could be solved through a “guess‐and‐check” strategy. There is a sample with
addition and one with subtraction. Definitions are also provided for: arithmetic expression,
algebraic expression and variable.
• Instructional Context: N/A
• How the content is best delivered: N/A
• How the audience will interact with the module: N/A
• How the learning module is designed to manage cognitive load: In the original example there is a
presence of split‐attention because the student must split their attention between the paragraphs
of definitions/explanations and the worked examples. The definitions presented are not particularly
relevant to the problems presented and would most likely add confusion. In the draft example, I
included the definitions with visuals, showed the equations being solved as a step‐by‐step process
and highlighted numbers where students would need to focus their attention.

23. Original
(Example 2)
Expressions and Equations
An arithmetic expression consists of numbers and operations using parentheses,
exponents, multiplication, division, addition, and subtraction. An algebraic expression is
like an arithmetic expression, but contains at least one variable. A variable is a letter that
represents a number. The equality of two expressions gives an equation. To solve an
equation means to find the value of the variable that will make the equation true.
Examples:
p + 4 = 11 x−3=9
p = 11 − 4 ← Use inverse operations. → x=9+3
p=7 x = 12

24. Draft
(Example 2)
Solving Simple Equations
Solve for p:
p + 4 = 11
Step 1
Identify the variable
p + 4 = 11
A variable is a letter or
symbol that stands for a
number
Step 2
Isolate the variable by using the inverse operation on both
sides of the equal sign
p + 4 = 11
- 4 -4
p + 0 = 7
Step 4
Applying the Zero Property of Addition, notice that the + 0
in the problem can be removed and you have solved for your variable.
p + 0 = 7
p = 7

25. Solving Simple Equations
Solve for x:
x - 3= 9
Step 1
Identify the variable
x - 3= 9
A variable is a letter or
symbol that stands for a
number
Step 2
Isolate the variable by using the inverse operation on both
sides of the equal sign
x - 3 = 9
+ 3 +3
x + 0 = 12
Step 4
Applying the Zero Property of Addition, notice that the + 0
in the problem can be removed and you have solved for your variable.
x + 0 = 12
x = 12

26. Worked Example 3
Making a Double Bar Graph
http://www.eduplace.com/
Scope of Worked Example 3
• Audience:
o Age: 9‐13
o Gender: male or female
o Reading level: beginning reading level
o Motivation: Knowing how to create a double bar graph
• Prerequisites for Project: Student must have prior knowledge in reading tables.
• Learning Module Goal:
o Objectives: Student will create a double bar graph using provided table of data.
o Type of task: N/A
o Transfer context: N/A
o Assessment: N/A
• How module addresses learner motivation: N/A
• Performance gap addressed by the module: N/A
Instructional Media Choices:
• Learning Module’s Content: This example provides the student the steps required to create a
double bar graph with a provided table of data. It also includes a finished double bar graph.
• Instructional Context: N/A
• How the content is best delivered: N/A
• How the audience will interact with the module: N/A
• How the learning module is designed to manage cognitive load: In the original example there is a
presence of split‐attention because the student must split their attention between table, the
introduction paragraphs, the steps listed, and the double bar graph provided. In the draft example, I
included the definitions with visuals, showed the equations being solved as a step‐by‐step process
and highlighted numbers where students would need to focus their attention. Presenting the
information in this manner will allow students to see each step as they move through the creation
of their double bar graph rather than only seeing the finished product and trying to decipher which
steps relates to each part of the finished product.

27. Original
(Example 3)

28. Draft
(Example 3)
Making a Double Bar Graph
Use the following table to make a Double Bar Graph:
Video and CD Collections
Students Number of Number of
Videos CD’s
Jay 17 32
Tina 8 15
Adrianne 12 8
Di 26 32
Rosa 12 28
Step 1
Add a title
Video and CD Collections
Number Number
Students
of Videos of CD’s
Video and CD Collections
Jay 17 32
Tina 8 15
Adrianne 12 8
Di 26 32
Rosa 12 28

29. Step 2
Label each Axis
Video and CD Collections
Video and CD Collections
Number Number
Number
Students of Videos of CD’s
Jay 17 32
Tina 8 15
Adrianne 12 8
Di 26 32
Rosa 12 28
Students
Step 3
Choose a scale & mark equal intervals
Add student names to horizontal axis
Video and CD Collections
Video and CD Collections Students of Videos Number
Number
of CD’s
Jay 17 32
40 Tina 8 15
Adrianne 12 8
Number
30 Di 26 32
20 Rosa 12 28
10
0
Jay Tina Adrianne Di Rosa
All numbers are
between 0 and 40
Students

30. Step 4
Draw bars for each student using 2 different colors
Video and CD Collections Video and CD Collections
Students of Videos Number
Number
of CD’s
40 Jay 17 32
Tina 8 15
Number
30 Adrianne 12 8
20 Di 26 32
Rosa 12 28
10
0
Jay Tina Adrianne Di Rosa
Students
Step 3
Make a key to show what each bar represents
Video and CD Collections
Video and CD Collections
Students of Videos Number
Number
of CD’s
40
Jay 17 32
Number
30 Tina 8 15
Adrianne 12 8
20 Di 26 32
10 Rosa 12 28
0
Jay Tina Adrianne Di Rosa
Students Number of Videos
Number of CDs