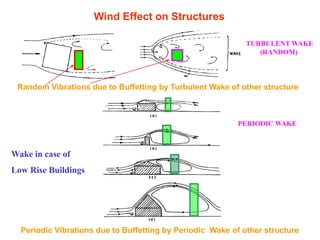
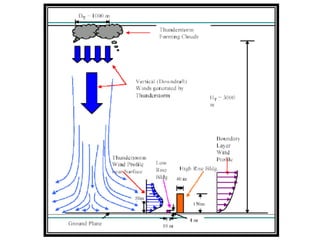
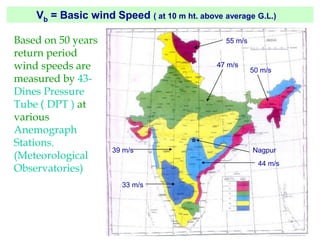
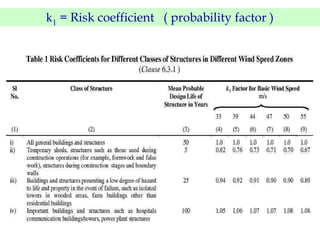
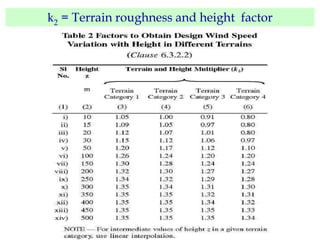
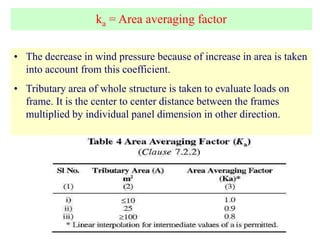
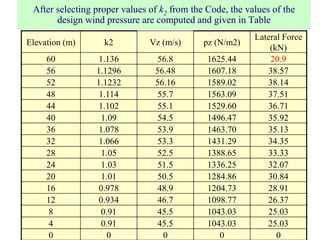
This document discusses wind load design for tall buildings. It states that wind load is the most important factor for buildings over 10 storeys tall. Wind loads are estimated using static and dynamic approaches. The document also provides guidance on instrumentation for monitoring wind data on tall structures, types of wind effects, dynamic wind analysis procedures, code provisions for wind speed and pressure calculations, and examples calculating wind loads using force coefficient and gust factor methods.

1. Wind load
• Most important factor that determines the design
of tall buildings over 10 storeys, where storey
height approximately lies between 2.7 – 3.0 m
• Appropriate design wind loads are estimated
based on:
– Static approach
– Dynamic approach

2. As per IS-875 (P3)2015
• All individuals and organizations responsible for putting-up
of tall structures ( transmission towers, chimneys, cooling
towers, buildings, etc ) to provide instrumentation in their
existing and new structures at different elevations ( at least at
two levels ) to continuously measure and monitor wind data.
• The instruments are required to collect data on wind
direction, wind speed and structural response of the structure
due to wind (with the help of accelerometer, strain gauges,etc)

3. Wind Effect on Structures

4. Wind Effect on Structures
Wake in case of
Low Rise Buildings
Wake
Wake
TURBULENT WAKE
(RANDOM)
PERIODIC WAKE
Random Vibrations due to Buffetting by Turbulent Wake of other structure
Periodic Vibrations due to Buffetting by Periodic Wake of other structure

6. Dynamic Wind Analysis
# For tall, long span and slender structures a ‘dynamic analysis’
of the structure is essential.
# Wind Gusts cause fluctuating forces on the structure
which induce large dynamic motions / oscillations.
# The severity of the wind-induced dynamic motions /
oscillations depends on - the natural frequency of vibration &
- the damping of the structure.
# Dynamic motions are induced in both directions -
- ‘along-wind’ direction as well as ‘across-wind’ direction.
# The ‘along-wind’ response of the structure is accounted for by
a magnification factor (‘gust factor’) applied to static forces.
# The ‘across-wind’ response requires a separate “dynamic -
analysis”.

7. Provisions of IS 875: 1987 (SP-64, 2001) can be broadly classified as:
• Computation of design wind speed based on wind zone, terrain
category, topography and wind direction.
• Computation of design wind pressure.
• Computation of wind load using pressure coefficients.
(Pressure coefficients are applicable to design of structural
elements like walls, roofs and cladding.)
• Computation of wind load using force coefficients.
(Force coefficients applicable to the building frame / structural
frameworks as a whole)
• Computation of along-wind forces using gust factor method to
account for dynamic effect of wind.
• Evaluation of across-wind forces using wind tunnel - model
analysis.
(Magnification factor applied to static forces)

8. Force Coefficient Method

9. A multistoried framed building
Length : 50 m
Width : 10 m
Height : 60 m
Height of each storey : 4 m
Spacing of frames : 5 m
along the length
5 m 5 m
4 m
15 @ 4 m
A MULTISTORY BUILDING
Example 1

10. Wind Data
Wind zone : 5 (Basic wind speed = 50 m/s)
Terrain category : 3
Topography : Flat (i.e. upwind slope < 3°)
Life of structure : 50 years.
Structure is present in non cyclonic region.

11. Terrain classification :
Category 1 - Open terrain with few or no obstructions. Average height of
object surrounding the structure is less than 1.5 m. (Open sea
coasts, flat plains without trees). Equivalent aerodynamic
roughness height (z0,1) for this terrain is 0.002 m.
Category 2- Open terrain with well scattered obstructions having height
between 1.5 to 10 m. (Airfields, open park lands, undeveloped
sparsely built-up outskirts of towns and suburbs). Equivalent
aerodynamic roughness height (z0,2) for this terrain is 0.02 m.
Category 3- Terrain with numerous closely spaced obstruction having
height upto 10 m with or without a few isolated tall structures.
(Well wooded areas and shrubs, town or industrial areas full or
partially developed). Equivalent aerodynamic roughness height
(z0,3) for this terrain is 0.2 m.
Category 4- Terrain with numerous large high closely spaced obstructions
generally with height above 25 m. (Large city centers, well
developed industrial complexes). Equivalent aerodynamic
roughness height (z0,4) for this terrain is 2 m.
As per IS 875 (part 3) 2015

12. Design Wind Speed (Vz)
Where,
VZ = Design wind speed at any height z (m/s)
Vb = Basic wind Speed
k1 = Risk coefficient (probability factor ) ( Cl. No. 6.3.1 )
k2 = Terrain roughness and height factor ( Cl. No. 6.3.2 )
k3 = Topography factor ( Cl. No. 6.3.3 )
k4 = Importance factor for cyclonic region ( Cl. No. 6.3.4 )
Vz = Vb . K1 . K2 . K3 .K4

13. Vb = Basic wind Speed ( at 10 m ht. above average G.L.)
55 m/s
50 m/s
47 m/s
44 m/s
33 m/s
39 m/s
*
Nagpur
Based on 50 years
return period
wind speeds are
measured by 43-
Dines Pressure
Tube ( DPT ) at
various
Anemograph
Stations.
(Meteorological
Observatories)

14. k1 = Risk coefficient ( probability factor )

15. k2 = Terrain roughness and height factor

16. k3 = Topography factor
CL.6.3.3.1 When upwind slope (θ ) greater than 3˚ then
k3 = 1.0 to 1.36
k3 = 1.0 for slopes less than 3˚.
( Refer Appendix C )
It may be noted that the value of k3 is maximum near the ground,
and reducing to 1.0 at higher levels.

17. k4 = Importance factor for cyclonic region
• This factor is added in the latest to consider the effect of severe cyclone
winds.
• East coast and west coast (Gujarat) are vulnerable for the occurrence of
cyclone storms.
• The effect of cyclonic storms is largely felt in a belt of 60 km width at
the coast.
• The following values of k4 are taken according to the importance of the
structure.

18. Therefore, Design Wind Speed is given by,
Vz = Vb.k1.k2.k3.k4
k1 = 1.00
k2 = varies with height
k3 = 1.00
k4 = 1.00
Vz = (50 x 1 x 1 x 1) k2
= 50 k2 m/s
Design Wind Speed (velocity)

19. Design Wind Pressure (pd)
pz = 0.6 Vz2
pd = kd.ka.kc.pz
Where,
pz = Wind pressure at height z in (N/m2)
Vz = Design wind speed at any height z (m/s)
pd = Design wind speed
kd = Wind directionality factor ( Cl. No. 7.2.1 )
ka = Area averaging factor ( Cl. No. 7.2.2 )
kc = Combination factor ( Cl. No. 7.3.3.13 )
However, the value of pd shall not be less than 0.7pz

20. kd = Wind directionality factor
• It is specified that for buildings, solid signs, open signs, lattice
frameworks and trussed towers (triangular, square, rectangular) a
factor of 0.9 may be used on the design wind speed.
• For circular or near-circular forms this factor may be taken as 1.
• For cyclone affected regions the factor shall be taken as 1.

21. ka = Area averaging factor
• The decrease in wind pressure because of increase in area is taken
into account from this coefficient.
• Tributary area of whole structure is taken to evaluate loads on
frame. It is the center to center distance between the frames
multiplied by individual panel dimension in other direction.

22. kc = Combination factor
• It is not necessary that on frames of clad building the internal and
external pressure/suctions are always correlated (i.e. when
direction of internal and external pressure is same).
• Code suggests that, when taking wind loads on frames of clad
buildings combination factor of 0.9 may be taken.

23. Design Wind Pressure (pd)
Now,
pz = 0.6 Vz
2 = 0.6 x (50 k2)2 = 1500 k2
2 N/m2
For intermediate frames, Design Wind Pressure is
given by,
pd = kd x ka x kc x pz
kd = 0.9
Now, effective area at every node = 5 x 4 = 20 m2.
From table 4,
ka = 0.933
kc = 1.00
pd = 0.9 x 0.933 x 1 x 1500 k2
2
= 1259.55 k2
2 > 0.7 pz (1050 k2
2) ..OK

24. Design Wind Pressure (pd)
For roof frame, Design Wind Pressure is given by,
pd = kd x ka x kc x pz
kd = 0.9
Now, effective area at every node = 5 x 2 = 10 m2.
From table 4,
ka = 1.00
kc = 1.00
pd = 0.9 x 1 x 1 x 1500 k2
2
= 1350 k2
2 > 0.7 pz (1050 k2
2) ..OK

25. Wind Load Calculations
F = Cf Ae pd (Force coefficient Method : for structure as whole)
F = (Cpe- Cpi) A pd (Pressure coefficient Method : for individual
members like wall, roof, etc. )
Where,
F = Wind load
Cf = Force Coefficient
Ae = Effective frontal area obstructing wind
pd = Design wind pressure
Cpe = External pressure coefficient
Cpi = Internal pressure coefficient
A = Surface area of structural element or cladding unit

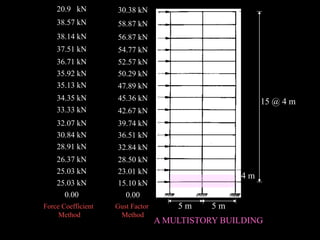
26. Wind Load Calculations
F= Cf Ae pd
a/b = 10/50= 0.2
h/b = 60/50= 1.2
Cf [refer Fig.4] = 1.2
Fig.4 : IS 875
a =10 m
b=50 m
Plan of building
a =10 m
h=60 m
Elevation
Frames @ 5m c/c
Frame
4m

27. Sample Calculation
Cf = 1.2
pd = 1259.55 k2
2
K2 = 1.136 (at ht. 60 m)
( refer Table 2, by interpolation between ht. 50-100 for terrain
category 3)
For top roof,
Ae = 5 x 2 = 10 m2 (Spacing of frames 5 m along the length &
half height of top storey = 2 m)
For intermediate floors,
Ae = 5 x 4 = 20 m2 (Taking height = 4 m)
10 m
50 m
Plan of Building
Frames @ 5m c/c
Wind
5m

28. F = Cf Ae pd
= 1.2 x 10 x 1742.17
= 20906 N
= 20.9 kN
Therefore, for top roof
pd = 1350 k2
2
= 1350 x (1.136)2
= 1742.17 N/m2
Therefore, for intermediate level
F = Cf Ae pd
= 1.2 x 10 x 1350 k2
2
= 16200 k2
2 kN

29. Elevation (m) k2 Vz (m/s) pz (N/m2)
Lateral Force
(kN)
60 1.136 56.8 1625.44 20.9
56 1.1296 56.48 1607.18 38.57
52 1.1232 56.16 1589.02 38.14
48 1.114 55.7 1563.09 37.51
44 1.102 55.1 1529.60 36.71
40 1.09 54.5 1496.47 35.92
36 1.078 53.9 1463.70 35.13
32 1.066 53.3 1431.29 34.35
28 1.05 52.5 1388.65 33.33
24 1.03 51.5 1336.25 32.07
20 1.01 50.5 1284.86 30.84
16 0.978 48.9 1204.73 28.91
12 0.934 46.7 1098.77 26.37
8 0.91 45.5 1043.03 25.03
4 0.91 45.5 1043.03 25.03
0 0 0 0 0
After selecting proper values of k2 from the Code, the values of the
design wind pressure are computed and given in Table

30. 5 m 5 m
4 m
15 @ 4 m
A MULTISTORY BUILDING
20.9 kN
38.57 kN
38.14 kN
37.51 kN
36.71 kN
35.92 kN
35.13 kN
34.35 kN
33.33 kN
32.07 kN
30.84 kN
28.91 kN
26.37 kN
25.03 kN
25.03 kN
0
Force Coefficient
Method

31. Gust Factor Method
Note that : Wind induced oscillations / excitation
may occur at wind speeds lower than
the static design wind speed for the location.
Along-wind Dynamic Analysis
For structures with high slenderness ratio
Tall-buildings, Chimneys, Latticed-towers, Cooling-towers, Transmission-
towers, Guyed-masts, Communication-towers, Long-span-bridges
* Magnitude of fluctuating component of wind velocity is called Gust.
* Gust causes increase in air pressure.

32. A muti-storeyed framed building
Given:
Physical Parameters:
Building : 50 m long,
10 m wide
60 m high
Life of structure : 50 years
Terrain category : 3
Topography : Flat
Location : Bhubneshwar
Example 2
5 m 5 m
4 m
15 @ 4 m
A MULTISTORY BUILDING

33. Ratio of height to least lateral dimension, H/d = 60/10 = 6 > 5
Dynamic analysis is required
d
H
T 09
.
0

Time period for multi-storeyed building is given by
Natural Frequency ( f ) = 1 / 1.7 = 0.58 Hz < 1.0 Hz
Dynamic analysis is required
= 1.7 Sec.
With shear wall or bracings
First Mode
Dynamic effect : Wind induced oscillations / excitation

34. Turbulence Intensity (Iz,i)
Turbulence intensity is different for different terrain category:
• Terrain category 1
• Terrain category 2
• Terrain category 3
• Terrain category 4
where, z0,i = Equivalent aerodynamic roughness height for terrain
category ‘i’










1
,
0
10
1
, log
0535
.
0
3507
.
0
z
z
Iz
 
1
,
4
,
1
,
2
,
7
1
z
z
z
z I
I
I
I 


 
1
,
4
,
1
,
3
,
7
3
z
z
z
z I
I
I
I 












4
,
0
10
4
, log
1358
.
0
466
.
0
z
z
Iz

35. Design Hourly Mean Wind Speed (Vz’)
Vz’= Vb . k1 . k2’. k3 . k4
Equivalent aerodynamic
roughness height for
terrain ‘i’

36. Therefore, Design Hourly Mean Wind Speed is given by,
Vz’ = Vb . k1 . k2,i’ . k3 . k4
k1 = 1.00
k2,i’ = varies with height
k3 = 1.00
k4 = 1.00
Vz’ = (50 x 1 x 1 x 1) k2’
= 50 k2,i’ m/s
Now, Design Wind Pressure at height z
pd’= pz’= 0.6 (Vz’)2 = 0.6 x (50 k2,i’)2 = 1500 (k2,i’)2 N/m2
    7245
.
0
2
.
0
2
.
0
60
ln
1423
.
0
ln
1423
.
0
0706
.
0
0706
.
0
3
,
0
3
,
0
3
,
2 

































 z
z
z
k

37. For z = 60,
V60’ = 50 k2,3’ = 50 x 0.724 = 36.2 m/s
Similarly solve for z = 0, 4, 8, 12, . . . .(to) 56 at each level
pd’= pz’=1500 x 0.72452 = 787.3 N/m2
Similarly solve for z = 4, 8, 12, . . . .(to) 56 at each level
    724
.
0
2
.
0
2
.
0
60
ln
1423
.
0
ln
1423
.
0
0706
.
0
0706
.
0
3
,
0
3
,
0
3
,
2 

































 z
z
z
k

38. Along Wind Load
Along wind load on a strip area (Az) at any height (z)
Fz’ = Cf,z . Az . pz
’ . G
Where,
Fz’ = Along wind load at any height z corresponding to
strip-area Ae
Cf,z = Drag force coefficient for the building,
Az = Effective frontal area at height z,
pz
’ = Design pressure at height z due to hourly mean wind
G = Gust Factor
Gust factor is dependent on overall height (h) and
the height of level (s) under consideration.

39. Force coefficient for building
a/b = 10/50= 0.2
h/b = 60/50= 1.2
Cf ,z [refer Fig.4] = 1.2
Fig.4 : IS 875-P3
a =10 m
b=50 m
Plan of building
a =10 m
h=60 m
Elevation
Frames @ 5m c/c
Frame
4m
Effective frontal area at intermediate
level (Az) = 5 x 4 = 20 m2
At roof level = 5 x 2 =10 m2

40. ]
)
1
(
[
1
2
2
2


SE
g
H
B
g
r
G R
s
s
v 



Where,
gv = Peak factor for upwind velocity fluctuation
= 3.0 for category 1 and 2 terrains and,
= 4.0 for category 3 and 4 terrains
r = Roughness factor
= 2 times longitudinal turbulence intensity, Ih,i (Cl.No. 6.5)
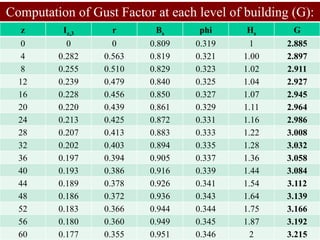
Computation of Gust Factor (G):

41. bsh = Average breadth of the building between height s and h.
Lh = Measure of effective turbulence length
…for terrain category 1 to 3
…for terrain category 4
h = Overall height of the building
s = Level at which action effects are calculated
z = Height of the frame considered from G.L.
Computation of Gust Factor (G):







 



h
sh
s
L
b
s
h
B
2
2
46
.
0
)
(
26
.
0
1
1
25
.
0
10
70 






h
Lh
25
.
0
10
85 






h
Lh

42. Lh = Measure of effective turbulence length
…for terrain category 1 to 3
= …for terrain category 4
= Factor to account for the second order turbulence intensity
Ih,i = Turbulence intensity at roof level and terrain category ‘i’
Hs = Height factor for resonance response
gR = Peak factor for resonant response
fa = First mode natural frequency of the building in Hz.
Computation of Gust Factor (G):
25
.
0
10
85 






h
Lh
25
.
0
10
70 






h
Lh

2
, s
i
h
v B
I
g


2
1 







h
s
H s
 
 
a
R f
g 3600
ln
2


43. S = Size reduction factor
b0h = average breadth of the building between 0 and h
E = Spectrum of turbulence in the approaching wind stream
N = Effective reduced frequency
= Design hourly mean wind speed at height h
β = Damping coefficient of the building ...Refer table below
Computation of Gust Factor (G):















d
h
h
a
d
h
a
V
b
f
V
h
f
S
,
0
,
4
1
5
.
3
1
1
  6
5
2
8
.
70
1 N
N
E



d
h
h
a
V
L
f
N
,

d
h
V ,

44. Solution:
By assuming s = z,
gv = 4 …for terrain category 3 …1
For z = 60 i.e at roof level,
r = 2 x I60,3 = 0.354 …2
Similarly solve for z = 0, 4, 8, 12, . . . .(to) 56 at each level
Computation of Gust Factor (G):
111
.
0
002
.
0
60
log
0535
.
0
3507
.
0 10
1
,
60 








I
265
.
0
2
60
log
1358
.
0
466
.
0 10
4
,
60 








I
  177
.
0
111
.
0
265
.
0
7
3
111
.
0
3
,
60 



I

45. bsh = 10 m
For s = 60,
…3
I60,3 = 0.177
…4
For s = 60,
…5
Similarly solve for s = 0, 4, 8, 12, . . . .(to) 56 at each level for
equation 3, 4 , and 5.
Computation of Gust Factor (G):
032
.
133
10
60
85
25
.
0








h
L
951
.
0
032
.
133
10
46
.
0
)
60
60
(
26
.
0
1
1
2
2








 




s
B
345
.
0
2
951
.
0
177
.
0
4





2
60
60
1
2









s
H

46. fa = 0.58 Hz
…6
V60’ = Hourly mean wind speed at top level = 36.2 m/s
b0,h = 10 m
…7
…8
Damping coefficient of building (β) = 0.02 …9
Computation of Gust Factor (G):
 
  909
.
3
58
.
0
3600
ln
2 


R
g
139
.
0
2
.
36
10
58
.
0
4
1
2
.
36
60
58
.
0
5
.
3
1
1






 







 



S
131
.
2
2
.
36
032
.
133
58
.
0



N
 
054
.
0
131
.
2
8
.
70
1
131
.
2
6
5
2






E

47. Gust factor for s = 60,
Similarly solve for s = 0, 4, 8, 12, . . . .(to) 56 at each level to find gust
factor for different floor levels.
Computation of Gust Factor (G):
21
.
3
]
02
.
0
054
.
0
139
.
0
909
.
3
2
)
3458
.
0
1
(
9515
.
0
4
[
3545
.
0
1
2
2
2










G
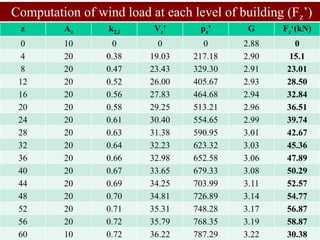
Along wind load (drag load) at roof top level
Fz’ = [ Cf,z . Az . pz
’ . G ] = 1.2 x 10 x 787.3 x 3.215 / 1000 = 30.37 kN
Similarly solve for s = 0, 4, 8, 12, . . . .(to) 56 at each level to find
lateral wind force for different floor levels.
Computation of Along Wind Load (Fz’):

48. z Iz,3 r Bs phi Hs G
0 0 0 0.809 0.319 1 2.885
4 0.282 0.563 0.819 0.321 1.00 2.897
8 0.255 0.510 0.829 0.323 1.02 2.911
12 0.239 0.479 0.840 0.325 1.04 2.927
16 0.228 0.456 0.850 0.327 1.07 2.945
20 0.220 0.439 0.861 0.329 1.11 2.964
24 0.213 0.425 0.872 0.331 1.16 2.986
28 0.207 0.413 0.883 0.333 1.22 3.008
32 0.202 0.403 0.894 0.335 1.28 3.032
36 0.197 0.394 0.905 0.337 1.36 3.058
40 0.193 0.386 0.916 0.339 1.44 3.084
44 0.189 0.378 0.926 0.341 1.54 3.112
48 0.186 0.372 0.936 0.343 1.64 3.139
52 0.183 0.366 0.944 0.344 1.75 3.166
56 0.180 0.360 0.949 0.345 1.87 3.192
60 0.177 0.355 0.951 0.346 2 3.215
Computation of Gust Factor at each level of building (G):

49. z Az k2,i Vz' pz' G Fz‘(kN)
0 10 0 0 0 2.88 0
4 20 0.38 19.03 217.18 2.90 15.1
8 20 0.47 23.43 329.30 2.91 23.01
12 20 0.52 26.00 405.67 2.93 28.50
16 20 0.56 27.83 464.68 2.94 32.84
20 20 0.58 29.25 513.21 2.96 36.51
24 20 0.61 30.40 554.65 2.99 39.74
28 20 0.63 31.38 590.95 3.01 42.67
32 20 0.64 32.23 623.32 3.03 45.36
36 20 0.66 32.98 652.58 3.06 47.89
40 20 0.67 33.65 679.33 3.08 50.29
44 20 0.69 34.25 703.99 3.11 52.57
48 20 0.70 34.81 726.89 3.14 54.77
52 20 0.71 35.31 748.28 3.17 56.87
56 20 0.72 35.79 768.35 3.19 58.87
60 10 0.72 36.22 787.29 3.22 30.38
Computation of wind load at each level of building (Fz’)

50. 5 m 5 m
4 m
15 @ 4 m
A MULTISTORY BUILDING
Force Coefficient
Method
30.38 kN
58.87 kN
56.87 kN
54.77 kN
52.57 kN
50.29 kN
47.89 kN
45.36 kN
42.67 kN
39.74 kN
36.51 kN
32.84 kN
28.50 kN
23.01 kN
15.10 kN
0.00
Gust Factor
Method
20.9 kN
38.57 kN
38.14 kN
37.51 kN
36.71 kN
35.92 kN
35.13 kN
34.35 kN
33.33 kN
32.07 kN
30.84 kN
28.91 kN
26.37 kN
25.03 kN
25.03 kN
0.00

51. The peak acceleration along wind direction at the top of
structure is given by the following formula :
a = ( 2 Π fa ) 2 δ gR . r (S E) / β
Where,
δ = Mean deflection at the point where the acceleration is
required.
Peak Acceleration at Top of Structure