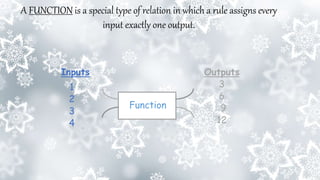
This document provides an overview of a math unit on functions. The unit will introduce students to the concept of functions, including defining functions, determining domain and range, evaluating functions, calculating slope, and representing functions in different ways. The unit consists of 4 lessons: defining functions, evaluating functions, comparing functions, and using functions to model linear relationships. Key learning objectives are outlined. Essential questions ask why functions are represented in multiple ways and how functional properties and operations are useful.

1. Housekeeping
Last week:
• Unit 1 Pretest – Functions
• MAP tests

2. Unit 1 Functions
Unit Summary: In this unit, students will be
introduced to the concept of
functions. Emphasis will be placed on the
definition of function, domain and range,
evaluating functions, calculating slope of a
linear function, identifying the rate of change of
a function and whether it is increasing or
decreasing, and representing functions in
different ways.

4. Learning Objectives:
Upon successful completion of this unit, students will be
able to:
• define function
• recognize a function and determine its domain and range
• evaluate a function using substitution
• calculate slope and compare rates of change for linear
functions
• construct an equation from a graph or table of values
• model real world situations with functions

5. Essential Questions/What is the Purpose for Learning
This?
Make sure you can answer these questions before
attempting the Unit Test.
Why are relations and functions represented in multiple
ways?
How are properties of functions and functional operations
useful?

6. Lesson Content
Lesson 1: Defining Functions--learn the definition of a function;
determine the domain and range; recognize when an equation is
not a function
Lesson 2: Evaluating Functions--use substitution to evaluate a
function; realize that for a function, every input has only one
output
Lesson 3: Comparing Functions--calculate slope; compare the rate
of change for various equations; represent functions in multiple
ways
Lesson 4: Using Functions to Model Linear Relationships--interpret
the rate of change from a model; identify if a function is increasing
or decreasing; construct and equation with information from a
graph or table

7. Lesson 1: Defining a Function
• learn the definition of a function
• determine the domain and range
• recognize when an equation is not a function

8. Why are functions important to me if I’m buying candy at the local
store?

11. In this lesson you will learn what a function is
by evaluating examples of relations.

12. A relation is any pairing of numbers.
Candy Bars to Price
Paul: (2 bars, $1.50)
You: (2 bars, $3.50)

13. Candy Palace
(2 bars, $1.50)
(2 bars, $3.50)
(3 bars, $5.00)
Sweet Factory
(1 bars, $0.75)
(2 bars, $1.50)
(3 bars, $2.25)
Two Kinds of
Relations

14. A FUNCTION is a special type of relation in which a rule assigns every
input exactly one output.
4
3
2
1
Inputs
12
9
6
3
Outputs
Function

15. Input (x) Output (y) Output (y)Input (x)
1
2
3
4
3
6
9
12
1
2
3
4
3
6
9
12
Function! Not a function!

16. A FUNCTION is a special type of relation in which a rule assigns every
input exactly one output.
Bars Price
1 $0.75
2 $1.50
3 $2.25
4 $3.00
Candy Bars to Price
Paul: (2 bars, $1.50)
You: (2 bars, $3.50)

17. Weeks Books
1 2
2 4
3 6
4 8
… …
Reading Two Books / Week
Is the Relation a Function???

18. Hours Problems Correct
1 34
1 65
2 42
2 32
3 53
4 67
Multiplication Facts
May
Cory
Barb
Susan
Silas
Lisa
If I tell you the
input, can you predict
the output?
Is the Relation a Function???

19. Input Output
1 3
2 6
3 9
4 12
Input Output
1 1
2 4
3 9
4 16
Input times 3 Input squared
Is the Relation a Function???

20. How do you figure out if a gumball machine models
a function relation?

21. Input (x) Output (y)

22. Input (x) Output (y)
1
2
3
2
4
6

23. Input (x) Output (y)
1
2
3
4
6
2

24. Input (x) Output (y)

25. Input (x) Output (y)
1
1
2
2
3
4

26. Input (x) Output (y)
1
2
2
3
4

27. A FUNCTION is a special type of relation in which a rule
assigns every input exactly one output.