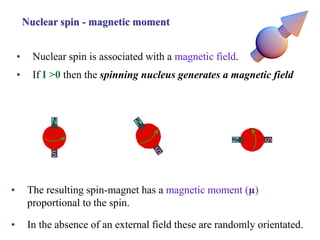
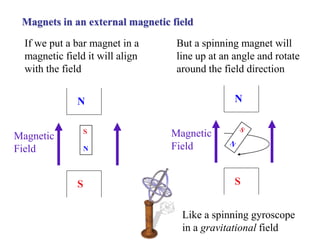
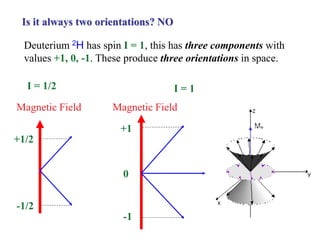
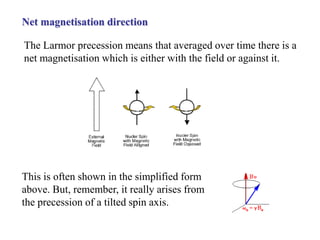
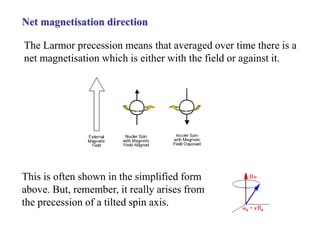
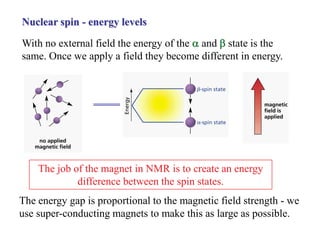
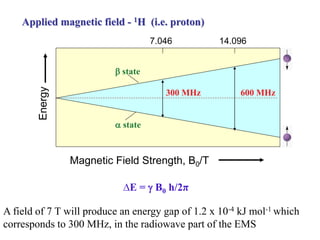
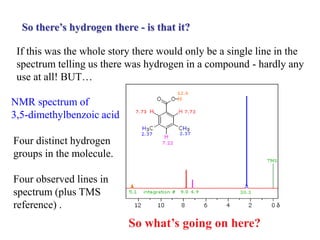
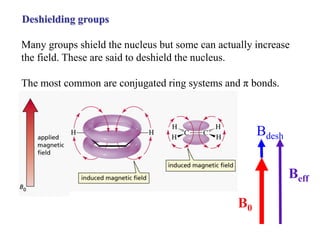
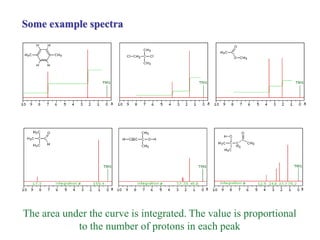
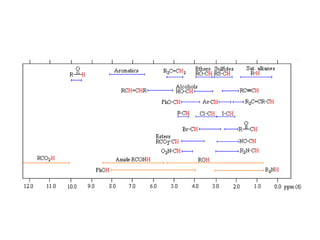
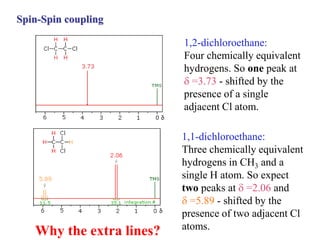
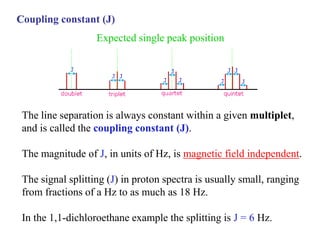
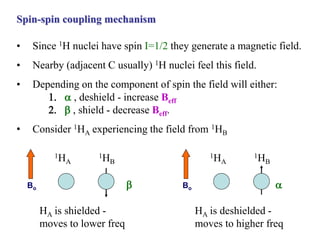
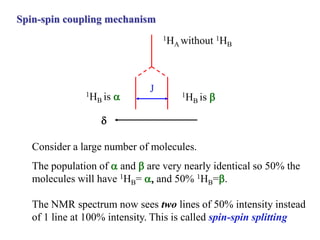
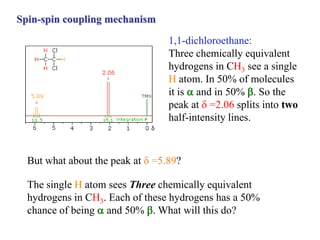
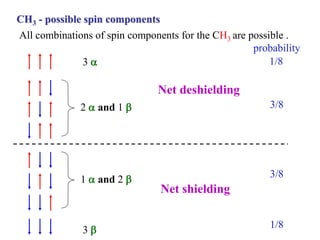
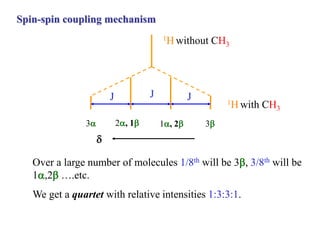
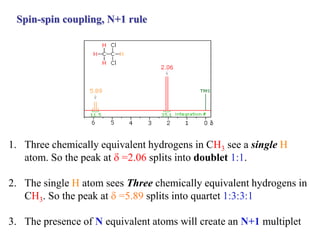
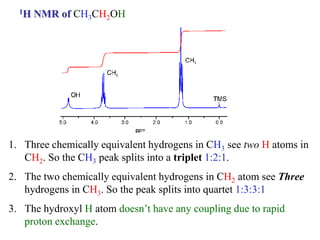
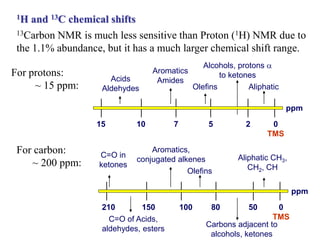
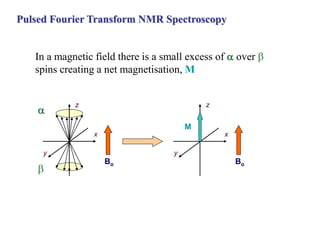
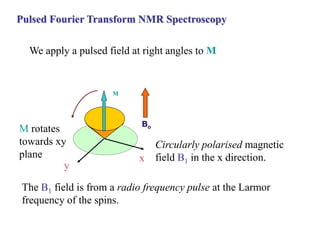
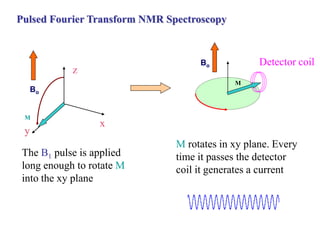
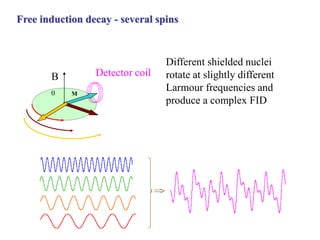
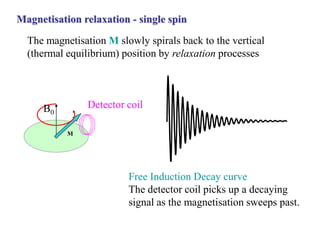
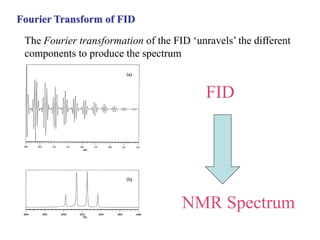
The document provides information on nuclear magnetic resonance (NMR) spectroscopy. It discusses key concepts such as nuclear spin, magnetic moments, energy levels of nuclei in magnetic fields, and spin-spin coupling. Nuclear spin gives rise to quantized magnetic moments and angular momentum. In an external magnetic field, these magnetic moments can align parallel or anti-parallel, splitting the energy levels. The energy difference between levels depends on the field strength and nucleus. NMR spectroscopy detects the absorption frequencies of nuclei as they transition between energy levels when irradiated with radio waves. Chemical shifts arise from electron shielding effects, allowing NMR to distinguish between similar nuclei. Spin-spin coupling further splits peaks into multiplets, providing detailed information about molecular structure.

1. Nuclear Magnetic Resonance (NMR) Spectroscopy
• The nuclei of many atoms have a property called nuclear spin (I)
• We can picture this as the nucleus ‘rotating’ - like the earth
• Any spinning object has angular momentum.
• In classical physics a body can have any value
of angular momentum.
This isn’t true at the atomic level.
This analogy should be treated with
caution. Nuclear spin is really a purely
quantum phenomenum

2. Nuclear spin is quantised
• The spin of subatomic particles (nuclei, electrons…) can only
have certain fixed values.
• We can think of this as ‘only particular rotation speeds are
possible’.
• We say that the angular momentum is quantised. This is the
basis of all of quantum theory used to describe motion at the
atomic level.

3. Nuclear spin - some common nuclei
• The spin is characterised by a quantum number, I
• Even mass nuclei composed of even numbers of protons
and neutrons have zero spin ( I = 0 ). So 12C, 16O have
ZERO spin.
• Nuclei with even number of protons and odd number of
neutrons have 1/2 integer spin
• Nuclei with odd numbers of protons and neutrons have
integer spin values.
Isotope % Abundance Spin (I)
1
H 99.98 1/2
2
H 0.016 1
11
B 81.17 3/2
13
C 1.11 1/2
19
F 100 1/2
31
P 100 1/2

4. Nuclear spin - magnetic moment
• The resulting spin-magnet has a magnetic moment (µ)
proportional to the spin.
• Nuclear spin is associated with a magnetic field.
• If I >0 then the spinning nucleus generates a magnetic field
• In the absence of an external field these are randomly orientated.

5. Magnets in an external magnetic field
If we put a bar magnet in a
magnetic field it will align
with the field
But a spinning magnet will
line up at an angle and rotate
around the field direction
Like a spinning gyroscope
in a gravitational field
N
S
S
N
Magnetic
Field
N
S
Magnetic
Field

6. A spinning nucleus in an external magnetic field can have only
certain orientations with respect to the field direction.
Nuclear spins in an external magnetic field
Spin I=1/2
N
S
Magnetic
Field
With the field direction.
Or against the field direction.

7. A particle with spin I=1/2 has two components +1/2 and -1/2.
We can picture this as being clockwise (+1/2) rotation or
anticlockwise (-1/2) rotation.
We refer to the two states as alpha, , and beta, , (just like
electrons which also have a spin of 1/2).
In an external field one lines up with the field and one against
I=1/2, Why two orientations?
Magnetic
Field


+1/2
-1/2

8. Deuterium 2H has spin I = 1, this has three components with
values +1, 0, -1. These produce three orientations in space.
Is it always two orientations? NO
Magnetic Field
+1/2
-1/2
I = 1/2
Magnetic Field
+1
-1
I = 1
0

9. Larmor precession
The spin axis will rotate around the direction of the field (like
the gyroscope under gravity). The angle is always the same.
Precession of the +1/2 component around
the field direction.
This is called Larmor precession.
The frequency of precession is given by 0 =  B0.
B0 is the field strength (in Tesla) and  is the magnetogyric ratio
(in T-1 s-1). This has a different value for every nucleus.

10. Net magnetisation direction
The Larmor precession means that averaged over time there is a
net magnetisation which is either with the field or against it.
This is often shown in the simplified form
above. But, remember, it really arises from
the precession of a tilted spin axis.

11. Net magnetisation direction
The Larmor precession means that averaged over time there is a
net magnetisation which is either with the field or against it.
This is often shown in the simplified form
above. But, remember, it really arises from
the precession of a tilted spin axis.

12. Nuclear spin - energy levels
With no external field the energy of the a and b state is the
same. Once we apply a field they become different in energy.
The energy gap is proportional to the magnetic field strength - we
use super-conducting magnets to make this as large as possible.
The job of the magnet in NMR is to create an energy
difference between the spin states.

13. Magnetic Field Strength, B0/T
Energy 7.046 14.096
300 MHz 600 MHz
a state
b state
Applied magnetic field - 1H (i.e. proton)
A field of 7 T will produce an energy gap of 1.2 x 10-4 kJ mol-1 which
corresponds to 300 MHz, in the radiowave part of the EMS
∆E =  B0 h/2π

14. Example
If the magnetogyric ratio for 1H is 26.7522 x 107 T-1 s-1
, calculate the magnetic field needed to
satisfy the resonance condition for protons
in a 550.0 MHz radiofrequency field.

15. Energy level populations, 1H
In most spectroscopy the lower state population is much greater
than the upper state. This is not the case in NMR.
• After a short time there will be a small population inbalance in
favour of the lower energy a state (thermal equilibrium).
Favour a state
• Only the population difference is responsible for a measurable
absorption. NMR signals are very weak.
Population difference
• Initially there are equal numbers in each a and b state.
Initially equal
a
b

16. NMR and organic compounds
1. Most organic molecules are made up of 12C, 1H, 16O, 14N.
2. Of these 12C and 16O have spin I=0 and hence no NMR
absorption.
3. 1H has spin I=1/2 and 14N has I=1 - so both have NMR
absorption (but in different spectral regions).
4. 2H with spin I=1 and 13C has I=1/2 are also used sometimes.
5. The vast majority of NMR is on the 1H nucleus.

17. NMR spectrometer - continuous wave
1. A sample is placed in a magnetic field and irradiated with radio
wave radiation at around 300MHz for a 7T field.
2. The radio frequency is scanned to measure a spectrum.
3. Alternatively the frequency is kept constant and the Magnetic
field scanned.
4. This approach is different to all other spectroscopy - here we use
a single photon frequency and adjust the energy level spacing to
match. This isn’t possible if the energy gap is already fixed.
Not to scale:
Magnets are large and
sample tube small

18. So there’s hydrogen there - is that it?
If this was the whole story there would only be a single line in the
spectrum telling us there was hydrogen in a compound - hardly any
use at all! BUT…
So what’s going on here?
NMR spectrum of
3,5-dimethylbenzoic acid
Four distinct hydrogen
groups in the molecule.
Four observed lines in
spectrum (plus TMS
reference) .

19. Shielding
1. Moving electrons generate a magnetic field (like electrons
flowing down a wire).
2. Electrons moving around a nucleus change the total field
experienced by the nucleus.
3. This electron circulation causes a small magnetic field,
Bsh = s B0 at the nucleus which opposes the external field B0.
Beff = B0 - Bsh = B0 (1-s)
Where s is a shielding constant .
B0
Beff
Bsh
4. The effective field at the nucleus is:

20. Shielding constants
1. Hydrogen nuclei will have different electron densities around
them depending on what chemical group they are attached to.
2. Hence different groups will have different shielding constants.
3. This means that hydrogen nuclei in different groups will have
slightly different absorption frequencies.

21. Deshielding groups
Many groups shield the nucleus but some can actually increase
the field. These are said to deshield the nucleus.
The most common are conjugated ring systems and π bonds.
B0
Beff
Bdesh

22. Chemical shift and the delta scale, d
The actual absorption frequencies depend on the magnet used in
the apparatus, making it difficult to compare spectra from
different machines. So the delta scale, is used instead.
The d scale uses a reference compound and records the
absorption of a peak, n, as a shift from the reference, nref. By
dividing by nref it becomes independent of the actual field - and
hence universal for all NMR machines.
The scale is normally given in parts per million, ppm, since the
shifts are very tiny.
d = n - nref
nref
 106 ppm

23. Because of molecular symmetry all
12 protons of TMS absorb at the same
frequency giving a strong single peak.
d scale reference - tetramethylsilane, TMS
• The silicon in TMS shifts the absorption peak far upfield.
• The vast majority of compounds have shifts downfield of TMS.
• The TMS peak is given d = 0 on the delta scale.

24. EXAMPLE
What is the shift of the resonance from TMS of
a group of protons with δ=6.33 ppm for a polypeptide
in a spectrometer operating at 420 MHz?

25. Some example spectra
The area under the curve is integrated. The value is proportional
to the number of protons in each peak

27. Spin-Spin coupling
1,2-dichloroethane:
Four chemically equivalent
hydrogens. So one peak at
d=3.73 - shifted by the
presence of a single
adjacent Cl atom.
1,1-dichloroethane:
Three chemically equivalent
hydrogens in CH3 and a
single H atom. So expect
two peaks at d=2.06 and
d=5.89 - shifted by the
presence of two adjacent Cl
atoms.
Why the extra lines?

28. Spin-Spin coupling
1. The patterns are symmetrically distributed on both sides of the
proton chemical shift position.
2. The central lines are always stronger than the outer lines.
3. The most commonly observed patterns are
• doublet (two equal intensity signals)
• triplet (three signals with an intensity ratio of 1:2:1)
• quartet (a set of four signals with intensities of 1:3:3:1)
• quintet (a set of five signals with intensities of 1:4:6:4:1).
The expected peaks have been split into a doublet at d=2.06 and a
quartet at d=5.89. Such spin-splittings are frequently observed at
high resolution.

29. Coupling constant (J)
The line separation is always constant within a given multiplet,
and is called the coupling constant (J).
The magnitude of J, in units of Hz, is magnetic field independent.
The signal splitting (J) in proton spectra is usually small, ranging
from fractions of a Hz to as much as 18 Hz.
In the 1,1-dichloroethane example the splitting is J = 6 Hz.
Expected single peak position

30. Spin-spin coupling mechanism
• Since 1H nuclei have spin I=1/2 they generate a magnetic field.
• Nearby (adjacent C usually) 1H nuclei feel this field.
• Depending on the component of spin the field will either:
1.  , deshield - increase Beff
2.  , shield - decrease Beff.
• Consider 1HA experiencing the field from 1HB
1HA
1HB
Bo
HA is deshielded -
moves to higher freq

1HA
1HB
Bo
HA is shielded -
moves to lower freq


31. Spin-spin coupling mechanism
1HA without 1HB
J
d
1HB is 
1HB is 
Consider a large number of molecules.
The population of  and  are very nearly identical so 50% the
molecules will have 1HB=  and 50% 1HB=.
The NMR spectrum now sees two lines of 50% intensity instead
of 1 line at 100% intensity. This is called spin-spin splitting

32. Spin-spin coupling mechanism
1,1-dichloroethane:
Three chemically equivalent
hydrogens in CH3 see a single
H atom. In 50% of molecules
it is  and in 50% . So the
peak at d =2.06 splits into two
half-intensity lines.
But what about the peak at d=5.89?
The single H atom sees Three chemically equivalent
hydrogens in CH3. Each of these hydrogens has a 50%
chance of being  and 50% . What will this do?

33. CH3 - possible spin components
All combinations of spin components for the CH3 are possible .
3 
2  and 1 
Net deshielding
1  and 2 
3 
Net shielding
1/8
3/8
3/8
1/8
probability

34. Spin-spin coupling mechanism
1H without CH3
J
d
3
Over a large number of molecules 1/8th will be 3, 3/8th will be
1,2 ….etc.
We get a quartet with relative intensities 1:3:3:1.
1, 2
2, 1
3
1H with CH3
J J

35. Spin-spin coupling, N+1 rule
1. Three chemically equivalent hydrogens in CH3 see a single H
atom. So the peak at d =2.06 splits into doublet 1:1.
2. The single H atom sees Three chemically equivalent hydrogens in
CH3. So the peak at d=5.89 splits into quartet 1:3:3:1
3. The presence of N equivalent atoms will create an N+1 multiplet

36. Pascal’s triangle
N
0
1
2
3
4
5
6
Multiplet Intensities
Pascal’s triangle is widely used in probability theory.
In it’s simplest use it gives the probability of getting the number
of heads/tails from tossing a coin N times. This is identical to
distributing  and  spins amongst N nuclei.

37. 1H NMR of CH3CH2OH
1. Three chemically equivalent hydrogens in CH3 see two H atoms in
CH2. So the CH3 peak splits into a triplet 1:2:1.
2. The two chemically equivalent hydrogens in CH2 atom see Three
hydrogens in CH3. So the peak splits into quartet 1:3:3:1
3. The hydroxyl H atom doesn’t have any coupling due to rapid
proton exchange.

38. 13C NMR
Has several uses:
1. Determining the number of different types of carbon atoms
present in the molecule. Hybridization has a strong affect:
sp3 carbons absorb at 0-100 ppm,
sp2 carbons at 100-220 ppm,
sp carbons at 70-100 ppm.
2. The electronic environment of the different types of carbons
(i.e. functional groups from the 13C chemical shifts).
3. The number of "neighbours" for a carbon (carbon-carbon
splittings are not observed: because 13C abundance is 1.1%, the
chance of 2 neighboring 13C atoms is about 0.01%.) - greatly
simplified compared to 1H spectrum.
CH3
H
C = C
C  CH
H

39. 1H and 13C chemical shifts
13Carbon NMR is much less sensitive than Proton (1H) NMR due to
the 1.1% abundance, but it has a much larger chemical shift range.
ppm
50
150 100 80
210
Aliphatic CH3,
CH2, CH
Carbons adjacent to
alcohols, ketones
Olefins
Aromatics,
conjugated alkenes
C=O of Acids,
aldehydes, esters
0
TMS
C=O in
ketones
For carbon:
~ 200 ppm:
0
TMS
ppm
2
10 7 5
15
Aliphatic
Alcohols, protons 
to ketones
Olefins
Aromatics
Amides
Acids
Aldehydes
For protons:
~ 15 ppm:

40. Pulsed Fourier Transform NMR Spectroscopy
Very much more efficient than the continuous method

41. Pulsed Fourier Transform NMR Spectroscopy
In a magnetic field there is a small excess of  over 
spins creating a net magnetisation, M
M
y
x
z
x
y
z
Bo Bo



42. Pulsed Fourier Transform NMR Spectroscopy
We apply a pulsed field at right angles to M
The B1 field is from a radio frequency pulse at the Larmor
frequency of the spins.
M
M rotates
towards xy
plane
Circularly polarised magnetic
field B1 in the x direction.
y
x
Bo

43. Pulsed Fourier Transform NMR Spectroscopy
The B1 pulse is applied
long enough to rotate M
into the xy plane
y
x
Bo
M
z
M rotates in xy plane. Every
time it passes the detector
coil it generates a current
M
Detector coil
Bo

44. Free induction decay - several spins
B
0 M
Detector coil
Different shielded nuclei
rotate at slightly different
Larmour frequencies and
produce a complex FID

45. Magnetisation relaxation - single spin
The magnetisation M slowly spirals back to the vertical
(thermal equilibrium) position by relaxation processes
M
Detector coil
B0
Free Induction Decay curve
The detector coil picks up a decaying
signal as the magnetisation sweeps past.

46. Fourier Transform of FID
The Fourier transformation of the FID ‘unravels’ the different
components to produce the spectrum
FID
NMR Spectrum

47. 2D NMR