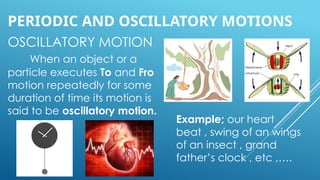
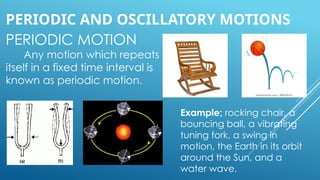
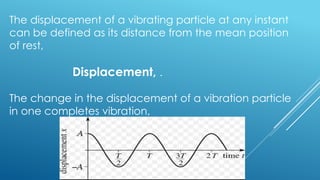
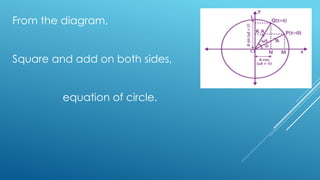
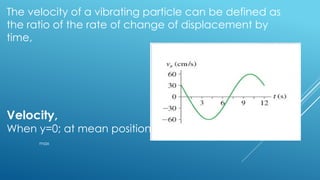
The document explains simple harmonic motion (SHM), describing its characteristics including displacement, velocity, and acceleration of a particle moving in a straight line towards a fixed point. It differentiates between oscillatory motion, which is repetitive to-and-fro movement, and periodic motion, which repeats over a fixed time interval. Various examples illustrate these concepts, including natural and mechanical oscillations.

1. WAVE AND OSCILLATION
SIMPLE HORMONIC MOTION
EXPRESSION FOR DISPLACEMENT , VELOCITY , ACCELERATION OF
A PARTICLE EXECUTING SHM

2. SIMPLE HARMONIC MOTION
If a particle moves in a straight
line , so that its acceleration is
always directed towards a fixed
point on the line , and is
proportional to its displacement
from the fixed point , the particle
is said to move with simple
harmonic motion .

3. PERIODIC AND OSCILLATORY MOTIONS
OSCILLATORY MOTION
When an object or a
particle executes To and Fro
motion repeatedly for some
duration of time its motion is
said to be oscillatory motion.
Example; our heart
beat , swing of an wings
of an insect , grand
father’s clock , etc ,….

4. PERIODIC MOTION
Any motion which repeats
itself in a fixed time interval is
known as periodic motion.
PERIODIC AND OSCILLATORY MOTIONS
Example; rocking chair, a
bouncing ball, a vibrating
tuning fork, a swing in
motion, the Earth in its orbit
around the Sun, and a
water wave.

5. EXPRESSION FOR DISPLACEMENT , VELOCITY ,
ACCELERATION OF A PARTICLE EXECUTING SHM
Let ‘P’ be a particle moving on the
circumference of a circle of ‘A’ with a uniform
angular velocity . ‘O’ is the center of the circle
. A perpendicular ‘PK’ is drawn from the
particle on the diameter ‘ YY’ ’ of the circle. As
the particle ‘P’ moves round the circle , the
foot of the perpendicular ‘K’ , vibrates along
the diameter ‘ YY’ ’. Since the motion of ‘P’ is
uniform , the motion of ‘K’ is periodic .As the
particle ‘P’ completes one revolution , the foot
of the perpendicular ‘K’ completes one
vertical oscillation. The distance ‘OK’ is called
the displacement and is denoted by ‘y’

6. The particle moves from ‘x’ to ‘P’ in time
‘t’.
Let,
From the
‘OK’ is called the displacement of the
vibrating particle.

7. The displacement of a vibrating particle at any instant
can be defined as its distance from the mean position
of rest,
Displacement, .
The change in the displacement of a vibration particle
in one completes vibration,

8. From the diagram,
Square and add on both sides,
equation of circle.

9. The velocity of a vibrating particle can be defined as
the ratio of the rate of change of displacement by
time,
Velocity,
When y=0; at mean position
max

10. The acceleration of a vibrating particle can be defined
as the ratio of the rate of change of velocity by time,
Thus, acceleration is directly proportional to
displacement and directed towards a fixed point. This
type of motion is called Simple Harmonic Motion.

11. THANK YOU
_RITHIKA.MP