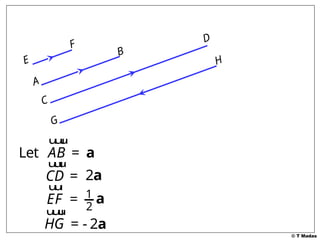
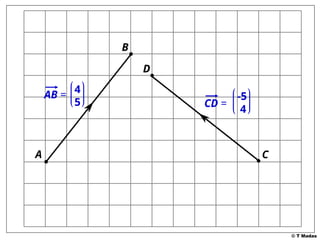
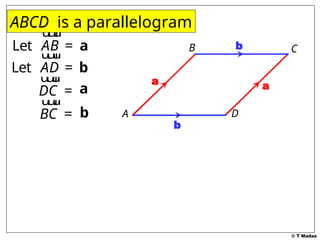
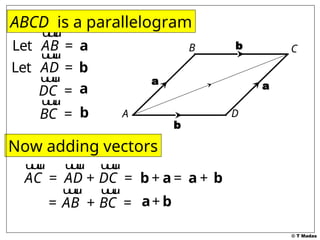
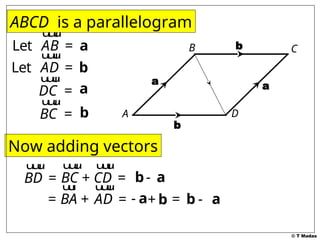
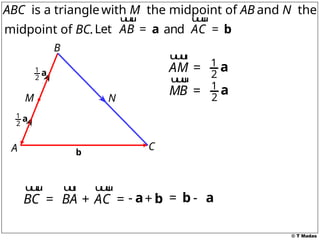
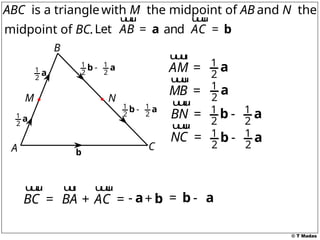
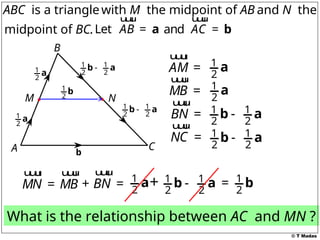
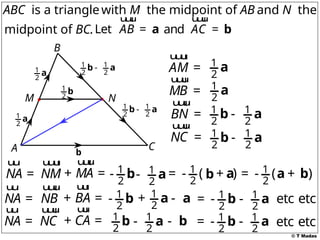
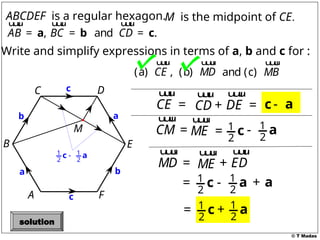
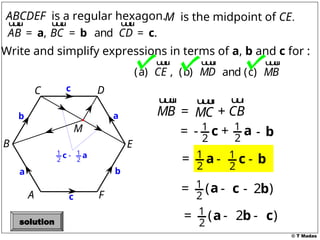
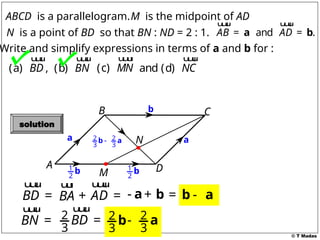
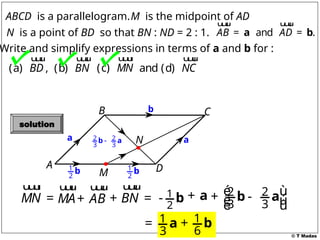
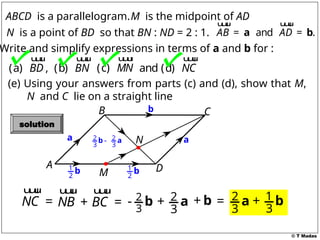
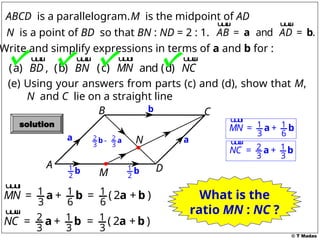
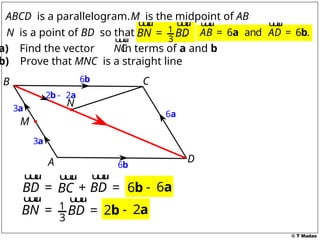
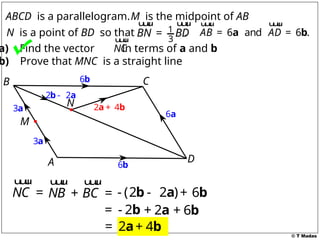
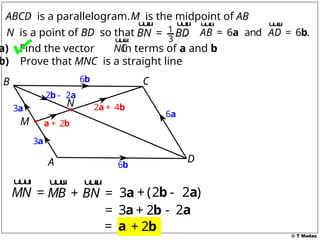
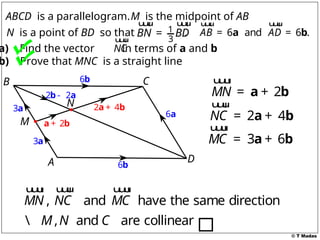
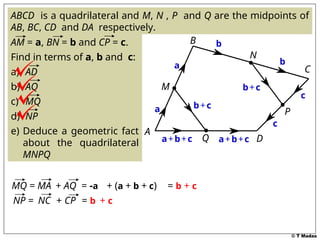
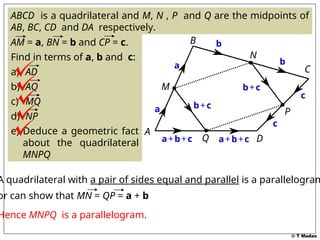
The document discusses vector concepts, focusing on their representation, addition, and the relationships between various geometric figures that can be formed with vectors. It covers specific cases such as parallelograms and triangles, emphasizing midpoints and vector notation in terms of components. Additionally, it presents exercises related to quadrilaterals and their properties, including conditions for parallelograms.

1. © T Madas
1
2
AB BC CD ( )
+ + = + + +
a b a b
u
u
r u
u
r u
u
r
2 3
+
i j

2. © T Madas
A vector is a line with a start and a finish.
It therefore has:
1. line of action
2. a direction
3. a given size (magnitude)
A B AB
u
u
u
r
= a
A B BA
u
u
r
-
= a

3. © T Madas
a
AB
u
u
u
r
a
we write vectors in the following ways:
By writing the starting point and the finishing point in
capitals with an arrow over them
With a lower case letter
which:
is printed in bold
or underlined when
handwritten
In component form if the vector is drawn on a
grid:
4
5

4. © T Madas
E
F
A
B
C
D
G
H
Let AB = a
u
u
u
r
CD =
u
u
u
r
2a
EF =
u
u
r
1
2
a
HG =
u
u
u
r
- 2a

5. © T Madas
4
5
A
B
-5
4
C
D
AB =
CD =

6. © T Madas

7. © T Madas
A
B C
D
Let AB = a
u
u
u
r
Let AD = b
u
u
u
r
a a
b
b
ABCD is a parallelogram
DC =
u
u
u
r
a
BC =
u
u
u
r
b

8. © T Madas
A
B C
D
Let AB = a
u
u
u
r
Let AD = b
u
u
u
r
a a
b
b
ABCD is a parallelogram
DC =
u
u
u
r
a
BC =
u
u
u
r
b
Now adding vectors
AC =
u
u
u
r
AD
u
u
u
r
DC
+ =
u
u
u
r
+ a
b = +
a b
AB
=
u
u
u
r
BC
+ =
u
u
u
r
+ b
a

9. © T Madas
A
B C
D
Let AB = a
u
u
u
r
Let AD = b
u
u
u
r
a a
b
b
ABCD is a parallelogram
DC =
u
u
u
r
a
BC =
u
u
u
r
b
Now adding vectors
BD =
u
u
u
r
BA
=
u
u
r
AD
+ =
u
u
u
r
+ b
- a = -
b a
BC
u
u
u
r
CD
+ =
u
u
u
r
- a
b

10. © T Madas

11. © T Madas
A
B
C
M
ABC is a triangle
N
with M the midpoint of AB and N the
midpoint of BC.Let AB = a
u
u
u
r
and AC = b
u
u
u
r
AM =
u
u
u
r
1
2
a
MB =
u
u
u
r
BC =
u
u
u
r
BA
u
u
r
AC
+ =
u
u
u
r
+ b
- a = -
b a
1
2
a
1
2
a
1
2
a
b

12. © T Madas
A
B
C
M
ABC is a triangle
N
with M the midpoint of AB and N the
midpoint of BC.Let AB = a
u
u
u
r
and AC = b
u
u
u
r
AM =
u
u
u
r
1
2
a
MB =
u
u
u
r
BN =
u
u
u
r
NC =
u
u
u
r
BC =
u
u
u
r
BA
u
u
r
AC
+ =
u
u
u
r
+ b
- a = -
b a
1
2
a
1 1
2 2
-
b a
1 1
2 2
-
b a
1
2
a
1
2
a
1 1
2 2
-
b a
1 1
2 2
-
b a
b

13. © T Madas
A
B
C
M
ABC is a triangle
N
with M the midpoint of AB and N the
midpoint of BC.Let AB = a
u
u
u
r
and AC = b
u
u
u
r
AM =
u
u
u
r
1
2
a
MB =
u
u
u
r
BN =
u
u
u
r
NC =
u
u
u
r
MN =
u
u
u
r
MB
u
u
u
r
BN
+ =
u
u
u
r
1 1
2 2
-
+ b a
1
2
a
1
2
a
1 1
2 2
-
b a
1 1
2 2
-
b a
1
2
a
1 1
2 2
-
b a
1 1
2 2
-
b a
1
2
= b
1
2
b
b
1
2
a
What is the relationship between AC and MN ?

14. © T Madas
1
2
- b
A
B
C
M
ABC is a triangle
N
with M the midpoint of AB and N the
midpoint of BC.Let AB = a
u
u
u
r
and AC = b
u
u
u
r
AM =
u
u
u
r
1
2
a
MB =
u
u
u
r
BN =
u
u
u
r
NC =
u
u
u
r
NA =
u
u
r
NM
u
u
u
r
MA
+ =
u
u
u
r
1
2
- b 1
2
- a
1
2
a
1 1
2 2
-
b a
1 1
2 2
-
b a
1
2
a
1 1
2 2
-
b a
1 1
2 2
-
b a
1
2
- ( )
=
1
2
b
b
1
2
a
b + a 1
2
- ( )
= +
a b
NA =
u
u
r
NB
u
u
u
r
BA
+ =
u
u
r
- a
1
2
+ a 1
2
-
= b 1
2
- a
1
2
b
NA =
u
u
r
NC
u
u
u
r
CA
+ =
u
u
r
- b
1
2
- a 1
2
-
= b 1
2
- a
etc etc
etc etc

15. © T Madas

16. © T Madas
ABCDEF is a regular hexagon.
, and .
AB BC CD
= = =
a b c
u
u
u
r u
u
u
r u
u
u
r
A
B
C D
M is the midpoint of CE.
E
F
M
a
b
c
Write and simplify expressions in terms of a, b and c for :
(a) ,
CE
u
u
u
r
(b) MD
u
u
u
r
and (c) MB
u
u
u
r
a
b
c
CE =
u
u
u
r
CD
u
u
u
r
DE
+ =
u
u
u
r
c- a
CM =
u
u
u
r
ME =
u
u
u
r
1
2
c 1
2
- a
1 1
2 2
-
c a
MD =
u
u
u
r
ME
u
u
u
r
ED
+
u
u
u
r
1
2
= c 1
2
- a + a
1
2
= c 1
2
+ a
solution

17. © T Madas
ABCDEF is a regular hexagon.
, and .
AB BC CD
= = =
a b c
u
u
u
r u
u
u
r u
u
u
r
A
B
C D
M is the midpoint of CE.
E
F
M
a
b
c
Write and simplify expressions in terms of a, b and c for :
(a) ,
CE
u
u
u
r
(b) MD
u
u
u
r
and (c) MB
u
u
u
r
a
b
c
1 1
2 2
-
c a
MB =
u
u
u
r
MC
u
u
u
r
CB
+
u
u
r
1
2
-
= c 1
2
+ a - b
1
2
- c
1
2
= a - b
1
2
( )
= a - c 2
- b
1
2
( 2 )
= - -
a b c
solution

18. © T Madas

19. © T Madas
M
A
B C
D
N
ABCD is a parallelogram.
and .
AB AD
= =
a b
u
u
u
r u
u
u
r
M is the midpoint of AD
Write and simplify expressions in terms of a and b for :
(a) ,
BD
u
u
u
r
(b) BN
u
u
u
r
and (d) NC
u
u
u
r
N is a point of BD so that BN : ND = 2 : 1.
(c) MN
u
u
u
r
a
1
2
b 1
2
b
a
b
2 2
3 3
-
b a
solution
BD =
u
u
u
r
BA
u
u
r
AD
+ =
u
u
u
r
- a+ b = -
b a
BN =
u
u
u
r
2
3
BD =
u
u
u
r
2
3
- a
2
3
b

20. © T Madas
M
A
B C
D
N
ABCD is a parallelogram.
and .
AB AD
= =
a b
u
u
u
r u
u
u
r
M is the midpoint of AD
Write and simplify expressions in terms of a and b for :
(a) ,
BD
u
u
u
r
(b) BN
u
u
u
r
and (d) NC
u
u
u
r
N is a point of BD so that BN : ND = 2 : 1.
(c) MN
u
u
u
r
a
1
2
b 1
2
b
a
b
MN =
u
u
u
r
MA
u
u
u
r
BN
+ =
u
u
u
r
1
2
- b + a
2 2
3 3
-
b a
AB
+
u
u
u
r 2 2
3 3
é ù
+ -
ê ú
ë û
b a
1
3
= a 1
6
+ b
solution

21. © T Madas
M
A
B C
D
N
ABCD is a parallelogram.
and .
AB AD
= =
a b
u
u
u
r u
u
u
r
M is the midpoint of AD
Write and simplify expressions in terms of a and b for :
(a) ,
BD
u
u
u
r
(b) BN
u
u
u
r
and (d) NC
u
u
u
r
N is a point of BD so that BN : ND = 2 : 1.
(c) MN
u
u
u
r
a
1
2
b 1
2
b
a
b
NC =
u
u
u
r
NB
u
u
u
r
2
3
- b 2
3
+ a
2 2
3 3
-
b a
BC
+ =
u
u
u
r
+ b 2
3
= a 1
3
+ b
(e) Using your answers from parts (c) and (d), show that M,
N and C lie on a straight line
solution

22. © T Madas
M
A
B C
D
N
ABCD is a parallelogram.
and .
AB AD
= =
a b
u
u
u
r u
u
u
r
M is the midpoint of AD
Write and simplify expressions in terms of a and b for :
(a) ,
BD
u
u
u
r
(b) BN
u
u
u
r
and (d) NC
u
u
u
r
N is a point of BD so that BN : ND = 2 : 1.
(c) MN
u
u
u
r
a
1
2
b 1
2
b
a
b
2 1
3 3
NC = +
a b
u
u
u
r
2 2
3 3
-
b a
(e) Using your answers from parts (c) and (d), show that M,
N and C lie on a straight line
1 1
3 6
MN = +
a b
u
u
u
r
2 1
3 3
NC = +
a b
u
u
u
r
1
3
( )
= 2a + b
1 1
3 6
MN = +
a b
u
u
u
r
1
6
( )
= 2a + b What is the
ratio MN : NC ?
solution

23. © T Madas

24. © T Madas
6 and 6 .
AB AD
= =
a b
u
u
u
r u
u
u
r
ABCD is a parallelogram.M is the midpoint of AB
a) Find the vector in terms of a and b
b) Prove that MNC is a straight line
1
3
BN BD
=
u
u
u
r u
u
u
r
N is a point of BD so that .
A
B C
D
M
NC
u
u
u
r
3a
3a
6b
6a
6b
BD =
u
u
u
r
BC
u
u
u
r
BD
+ =
u
u
u
r
6b 6
- a
BN =
u
u
u
r
1
3
BD =
u
u
u
r
2b 2
- a
2 2
-
b a
N

25. © T Madas
1
3
BN BD
=
u
u
u
r u
u
u
r
N is a point of BD so that . 6 and 6 .
AB AD
= =
a b
u
u
u
r u
u
u
r
ABCD is a parallelogram.M is the midpoint of AB
a) Find the vector in terms of a and b
b) Prove that MNC is a straight line
A
B C
D
M
NC
u
u
u
r
3a
3a
6b
6a
6b
2 2
-
b a
NC =
u
u
u
r
NB
u
u
u
r
- (2 2 )
-
b a
BC
+ =
u
u
u
r
6
+ b
- 2
= b 2
+ a 6
+ b
2
= a 4
+ b
2 4
+
a b
N

26. © T Madas
2
+
a b
1
3
BN BD
=
u
u
u
r u
u
u
r
N is a point of BD so that . 6 and 6 .
AB AD
= =
a b
u
u
u
r u
u
u
r
ABCD is a parallelogram.M is the midpoint of AB
a) Find the vector in terms of a and b
b) Prove that MNC is a straight line
A
B C
D
M
N
NC
u
u
u
r
3a
3a
6b
6a
6b
2 2
-
b a
2 4
+
a b
MN =
u
u
u
r
MB
u
u
u
r
(2 2 )
+ -
b a
BN
+ =
u
u
u
r
3a
2
- a
3
= a 2
+ b
= a 2
+ b

27. © T Madas
2
+
a b
1
3
BN BD
=
u
u
u
r u
u
u
r
N is a point of BD so that . 6 and 6 .
AB AD
= =
a b
u
u
u
r u
u
u
r
ABCD is a parallelogram.M is the midpoint of AB
a) Find the vector in terms of a and b
b) Prove that MNC is a straight line
A
B C
D
M
N
NC
u
u
u
r
3a
3a
6b
6a
6b
2 2
-
b a
2 4
+
a b
2
MN = +
a b
u
u
u
r
2 4
NC = +
a b
u
u
u
r
MC =
u
u
u
r
3 6
+
a b
, and have the same direction
MN NC MC
u
u
u
r u
u
u
r u
u
u
r
, and are collinear
M N C

28. © T Madas

29. © T Madas
ABCD is a quadrilateral and M, N , P and Q are the midpoints of
AB, BC, CD and DA respectively.
AM = a, BN = b and CP = c.
Find in terms of a, b and c:
a) AD
b) AQ
c) MQ
d) NP
e) Deduce a geometric fact
about the quadrilateral
MNPQ
A
B
C
D
M
N
P
Q
a
b
c
a b
c
AD = AB + BC + CD = 2a + 2b + 2c = 2(a + b + c)
AQ = a + b + c
a+b+c a+b+c

30. © T Madas
ABCD is a quadrilateral and M, N , P and Q are the midpoints of
AB, BC, CD and DA respectively.
AM = a, BN = b and CP = c.
Find in terms of a, b and c:
a) AD
b) AQ
c) MQ
d) NP
e) Deduce a geometric fact
about the quadrilateral
MNPQ
A
B
C
D
M
N
P
Q
a
b
c
a b
c
MQ = MA + AQ = -a + (a + b + c) = b + c
a+b+c a+b+c
b+c
NP = NC + CP = b + c
b+c

31. © T Madas
ABCD is a quadrilateral and M, N , P and Q are the midpoints of
AB, BC, CD and DA respectively.
AM = a, BN = b and CP = c.
Find in terms of a, b and c:
a) AD
b) AQ
c) MQ
d) NP
e) Deduce a geometric fact
about the quadrilateral
MNPQ
A
B
C
D
M
N
P
Q
a
b
c
a b
c
a+b+c a+b+c
b+c
b+c
A quadrilateral with a pair of sides equal and parallel is a parallelogram
or can show that MN = QP = a + b
Hence MNPQ is a parallelogram.

32. © T Madas