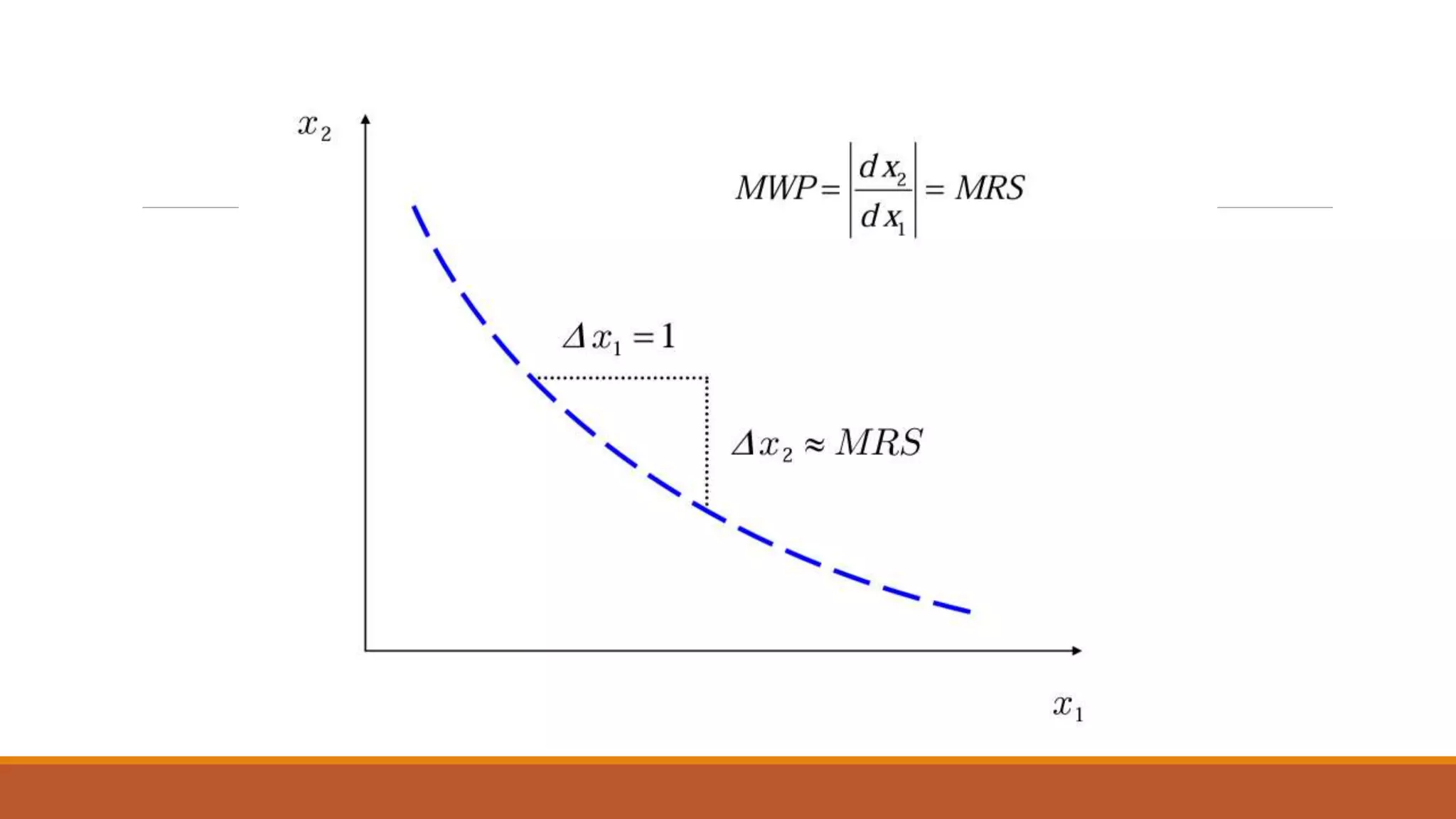
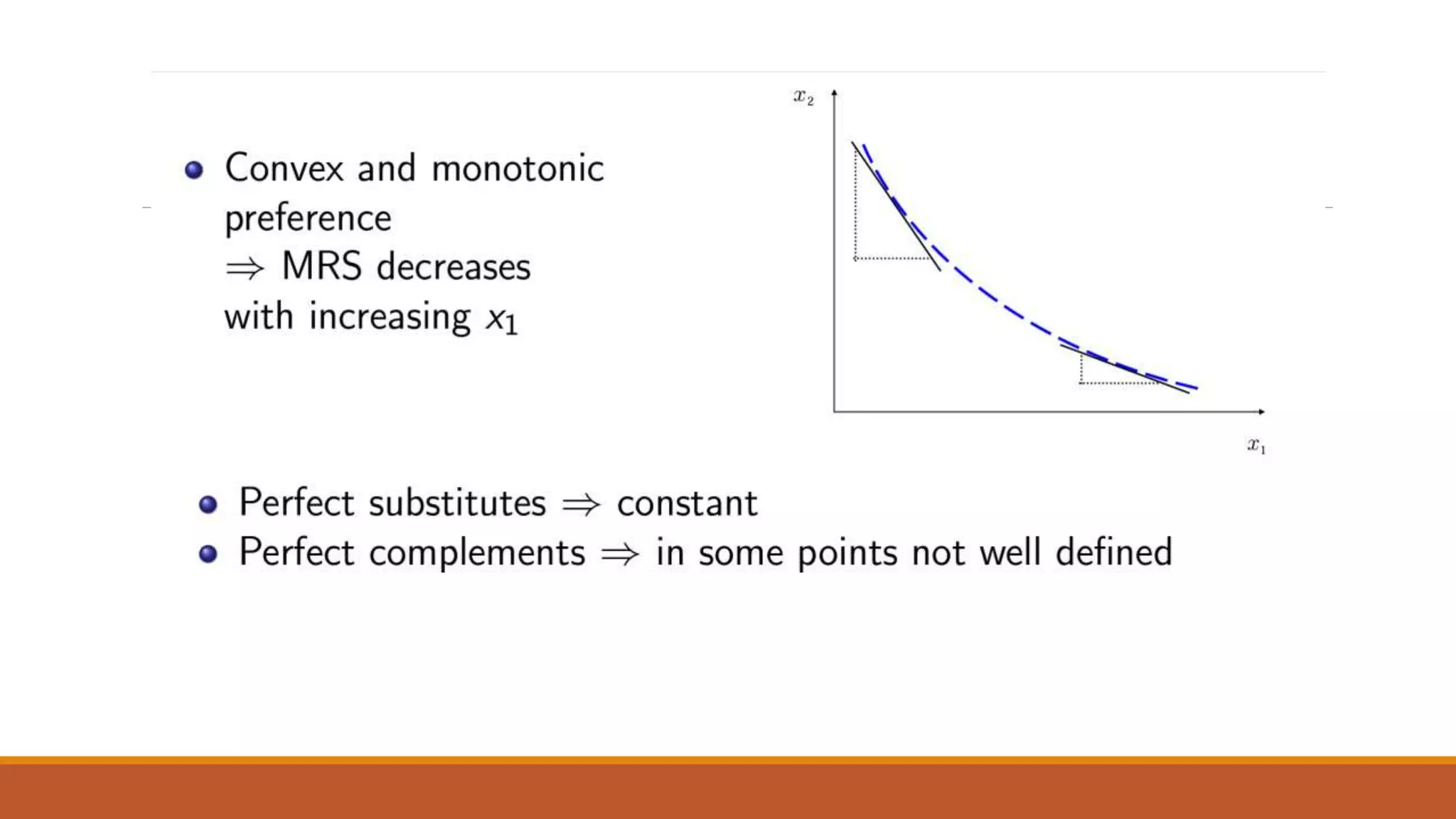
Utility and the Marginal Rate of Substitution are mathematically related through marginal utility. Marginal utility is defined as the increase in total utility from consuming one additional unit of a good, holding consumption of other goods constant. By fully differentiating the utility function U(X,Y), the relationship between marginal utility and the Marginal Rate of Substitution can be deduced. It is commonly assumed that marginal utility declines with additional consumption of a good due to decreasing marginal returns.

1. Utility and the Marginal
Rate of substitution

2. Utility and the Marginal Rate of Substitution are related through marginal Utility, which is defined as
follows:
Given a utility function U(X,Y), it is defines the Marginal Utility of X as the increase in utility generated by
the consumption of an additional unit of X, keeping the consumption of Y constant.
The magnitude of the UMgX is also arbitrary since it depends on how the original function U(X,Y) has been
defined. The relationship between UMgX is deduced as follows. Fully differentiating the function U(X,Y)
we have
solving we get the following relationship
It is also quite common to assume that the MU of the goods is decreasing

3. Decreasing marginal utility
To start, let us first suppose that an apple reported us a Total Utility of 4 utils when we ate it, later, with the second
apple we obtained a total Utility of 7 utils, and when we ate a third apple, we now get a utility of 8 and with a fourth
apple we have 9 utils just like with the fifth apple; but if we already eat a sixth our utility drops to 8 utils again. We can
put this in a table like the following:
Apples consumption Total U
0 0
1 4
2 7
3 8
4 9
5 9
6 8
This way of looking at utility, in terms of each unit of good (apples, for example), leads us to an important concept:
marginal utility.

4. Marginal utility
Marginal utility is the extra or additional utility obtained by consuming one more unit of a good or service
per unit of time. This marginal utility can be calculated by dividing the change in total utility by the change
in the number of units consumed.
𝑀𝑎𝑟𝑔𝑖𝑛𝑎𝑙 𝑢𝑡𝑖𝑙𝑖𝑡𝑦 =
∆𝑈𝑇
∆𝑈𝐶
Where
ΔUT= Increase of total utility
ΔUC= Increase of Units Consumed

5. Apples example
With the example of apples we have to calculate the Increase in Total Utility (UT) from 0 to 1, it would be as
follows:
Total Utility of 0 apples = 0
Total Utility of 1 apple = 4
ΔUT= 4
𝑀𝑎𝑟𝑔𝑖𝑛𝑎𝑙 𝑢𝑡𝑖𝑙𝑖𝑡𝑦 =
∆𝑈𝑇
∆𝑈𝐶
=
4
1
= 4

6. In the following cases, 3 and 4 apples consumed would be the same procedure. And nothing more would be to be careful in the
case of the 5th apple, where we would have the following: For the Increase of the Total Utility Total utility of 4 apples = 9
Total Utility of 5 apples = 9
ΔUT= 0
For the last case of the 6thapple, we have that the Marginal Utility would already be negative
For the Increase of the Total Utility
Total utility of 5 apples = 9
Total Utility of 6 apples = 8
ΔUT= - 1
The Increase of the Units consumed it would be 1, since from 5 to 6, the increase would be 1 extra or marginal unit.
𝑀𝑎𝑟𝑔𝑖𝑛𝑎𝑙 𝑢𝑡𝑖𝑙𝑖𝑡𝑦 =
∆𝑈𝑇
∆𝑈𝐶
=
−1
1
= −1