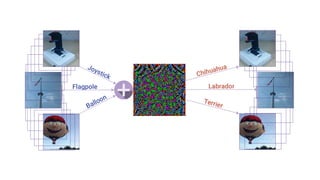
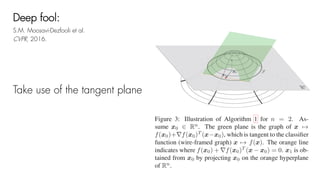
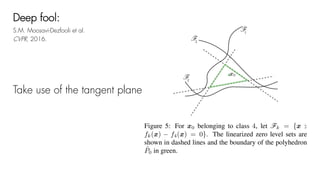
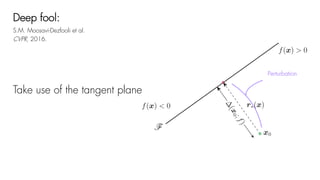
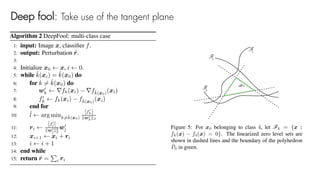
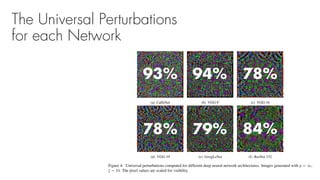
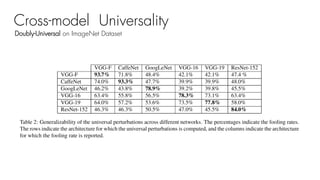
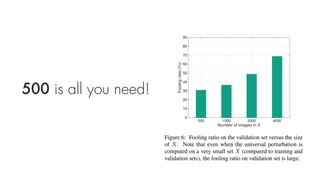
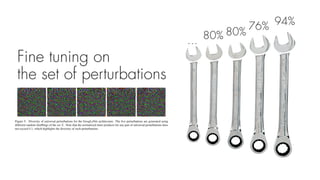
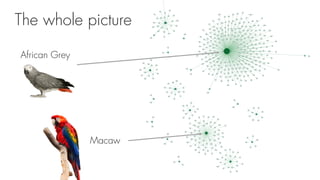
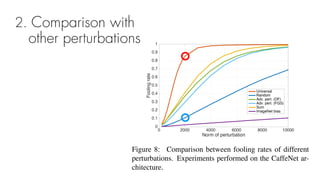
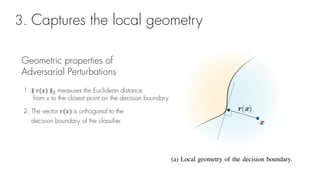
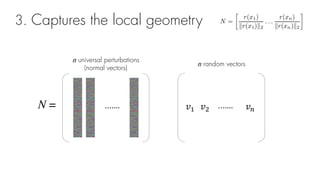
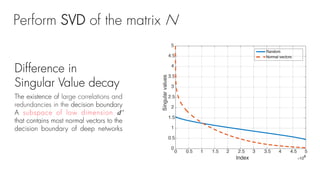
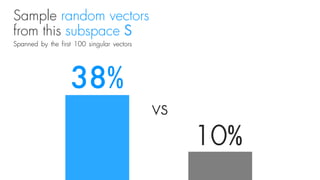
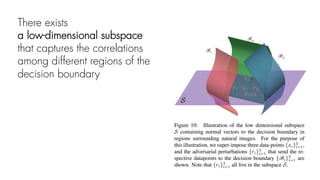
This document summarizes a seminar on universal adversarial perturbations. It begins with a quick introduction to adversarial attack methods like DeepFool. It then discusses the concept of universal adversarial perturbations - single perturbations that can fool neural networks into misclassifying most images. The document explains how universal perturbations are crafted to satisfy a fooling rate while being small. It shows that a single perturbation can achieve high fooling rates across different networks and models. It also discusses how universal perturbations capture the local geometry and correlations in the decision boundaries of neural networks.

1. U N I V E R S A L
A D V E R S A R I A L
2 0 1 8 S N U V L S E M I N A R
H Y U N W O O K I M
P E R T U R B A T I O N

2. C O N T E N T S
1. Quick Intro to Adversarial Attacks
- Deep fool: A simple and accurate method
to fool deep neural networks
- Explaining & Harnessing Adversarial Examples
2. Universal Adversarial Perturbation

3. Attacks ?

4. Through the
human eye
Anderson & Winawer, 2005

5. iPodBoat Perturbation
Through the
machine’s eye
Adversarial
Example or Attack

6. Intriguing Properties of Neural Networks
C. Szegedy et al. ICLR, 2014.

7. Intriguing Properties of Neural Networks
C. Szegedy et al. ICLR, 2014.

8. Explaining and Harnessing Adversarial Examples
I.J. Goodfellow et al. ICLR, 2015.

9. Explaining and Harnessing Adversarial Examples
I.J. Goodfellow et al. ICLR, 2015.
Fast Gradient Sign Method [FGSM]

10. !" = " + %
&
Fast Gradient Sign Method [FGSM]
Explaining and Harnessing Adversarial Examples
I.J. Goodfellow et al. ICLR, 2015.
Perturbation
Gradient of the
cost function

11. Fast Gradient Sign Method [FGSM]
Explaining and Harnessing Adversarial Examples
I.J. Goodfellow et al. ICLR, 2015.
RAW Images ATTACKED Images
With Maxout Network
Misclassification Rate
- MNIST : 89.4%

12. Fast Gradient Sign Method [FGSM]
Explaining and Harnessing Adversarial Examples
I.J. Goodfellow et al. ICLR, 2015.
RAW Images ATTACKED Images
With Conv Maxout Network
Misclassification Rate
- CIFAR-10 : 87.2%

13. Fast Gradient Sign Method [FGSM]
Explaining and Harnessing Adversarial Examples
I.J. Goodfellow et al. ICLR, 2015.
: Intensity of the Attack

14. Various methods of attacks

15. Ian Goodfellow

16. https://github.com/tensorflow/cleverhans
Python library for
Adversarial attacks

17. “They say that the best weapon
is the one you never have to fire.
I respectfully disagree.
I prefer the weapon
you only have to fire ONCE.”
-Tony Stark-

18. Universal
Adversarial
Perturbations
S.M. Moosavi-Dezfooli et al.
CVPR, 2017.

20. How to make one
• ! ∶ #$%&'$()&$*+ *, $-./0% $+ ℝ2
• 34 ∶ . 56.%%$,$5.&$*+ ,)+5&$*+ &ℎ.& *)&8)&% .+ 9:;<=>;9? @>A9@ 34 B
,*' 0.5ℎ $-./0 C ∈ ℝ2
E0 %00F . G05&*' H %)5ℎ &ℎ.&

21. How to make one:
constraints for the
!" #""$ % &"'()* + #,'ℎ (ℎ%(
+
2. Has to be small enough
1. Satisfies the fooling rate

22. ∆"#
∆"$
%
How to make one:
the algorithm

23. 2. Has to be small enough
1. Satisfies the fooling rate
Projection on the ℓ" ball of radius #

24. From another paper by the author

26. Take use of the tangent plane
Deep fool:
S.M. Moosavi-Dezfooli et al.
CVPR, 2016.

27. Take use of the tangent plane
Deep fool:
S.M. Moosavi-Dezfooli et al.
CVPR, 2016.

28. Take use of the tangent plane
Perturbation
Deep fool:
S.M. Moosavi-Dezfooli et al.
CVPR, 2016.

29. Deep fool: Take use of the tangent plane

30. 2. Has to be small enough
1. Satisfies the fooling rate

31. The one perturbation that
messes up with all the classes

32. The Universal Perturbations
for each Network
93% 94%
79%
78%
78% 84%

33. Doubly-Universal on ImageNet Dataset
Cross-model Universality

34. Cross-model Universality
Intriguing Properties of Neural Networks
C. Szegedy et al. ICLR, 2014.

35. Doubly-Universal on ImageNet Dataset
Cross-model Universality

36. Need many images for crafting ?

37. 500 is all you need!

38. How about fine tuning ?

39. Fine tuning on
the set of perturbations
94%76%
80%80%…

40. The real fun part

41. 1. The existence of
dominant labels

42. Been overlooked
Intriguing Properties of Neural Networks
C. Szegedy et al. ICLR, 2014.

43. The whole picture
African Grey
Macaw

44. Some examples

45. 2. Comparison with
other perturbations

46. 3. Captures the local geometry
Geometric properties of
Adversarial Perturbations
1. ∥ "($) ∥& measures the Euclidean distance
from x to the closest point on the decision boundary
2. The vector "($) is orthogonal to the
decision boundary of the classifier

47. …....
n universal perturbations
(normal vectors)
n random vectors
"# "$ ….... "%
3. Captures the local geometry
N =

48. Difference in
Singular Value decay
Perform SVD of the matrix N
The existence of large correlations and
redundancies in the decision boundary
A subspace of low dimension d’
that contains most normal vectors to the
decision boundary of deep networks

49. Sample random vectors
from this subspace S
Spanned by the first 100 singular vectors
10%
38%
vs

50. There exists
a low-dimensional subspace
that captures the correlations
among different regions of the
decision boundary

51. Generalization of
Universal perturbations

52. The Universal Adversarial Perturbation
A silver bullet1 single vector
Image-agnostic
Network-agnostic

53. I L L U S I O N S
Adversarial Attacks

54. Thank you
Hyunwoo Kim