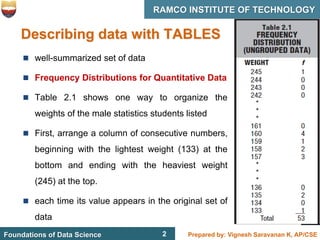
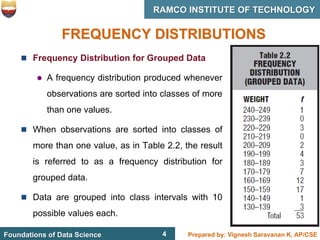
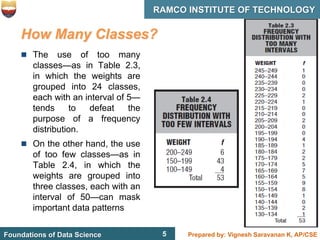
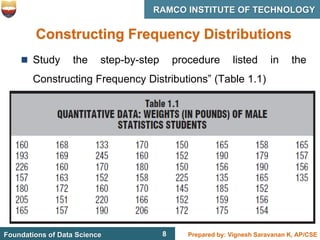
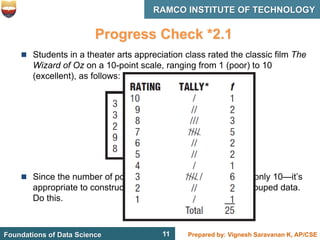
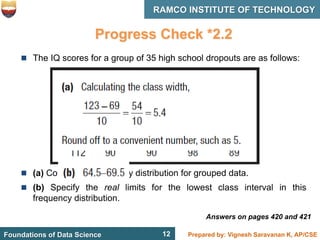
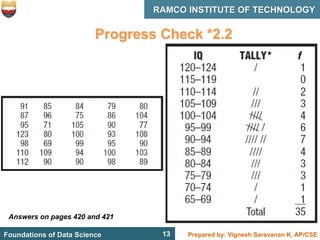
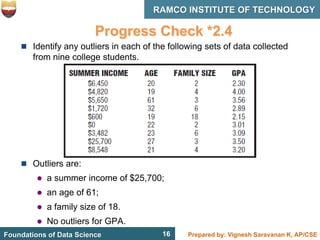
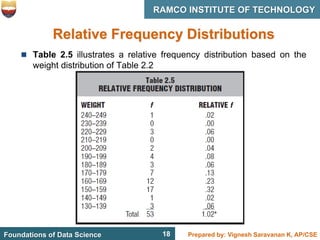
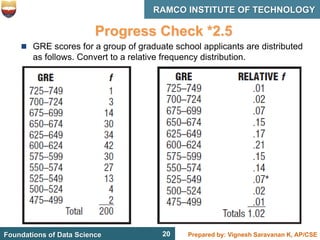
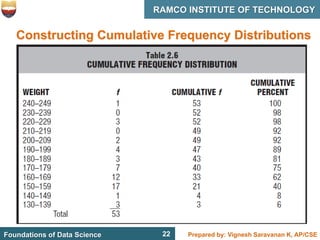
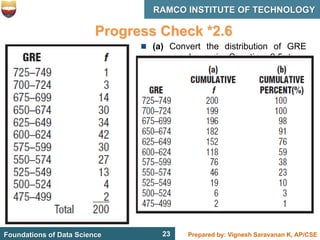
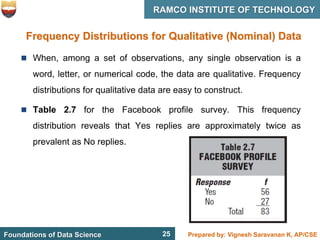
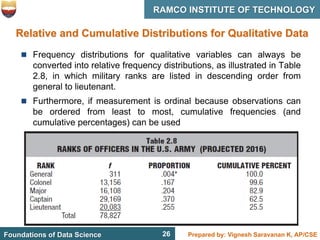
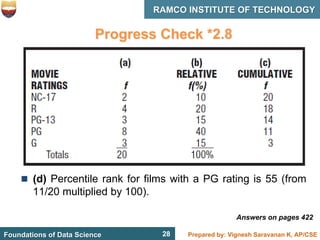
This document discusses describing data with tables and frequency distributions. It provides guidelines for constructing frequency distributions, including arranging the data into classes and calculating frequencies. Examples of constructing frequency distributions for quantitative and qualitative data are shown. Relative and cumulative frequency distributions are also discussed, along with calculating approximate percentile ranks. Progress checks with sample data are included to allow practice applying the concepts.