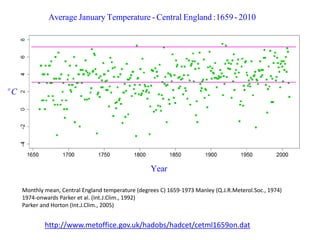
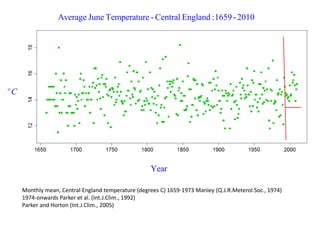
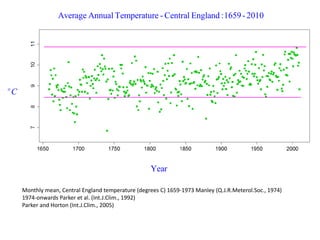
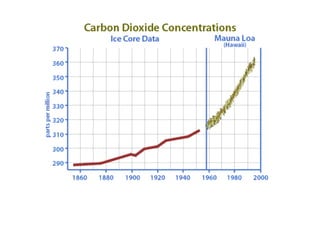
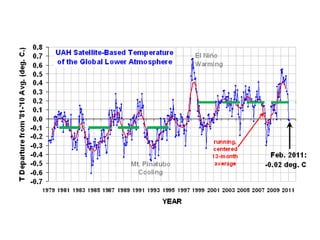
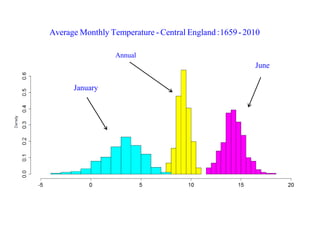
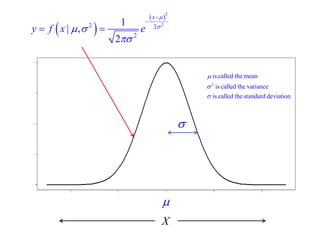
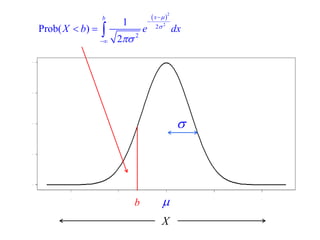
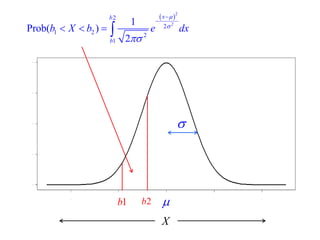
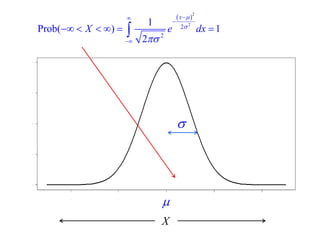
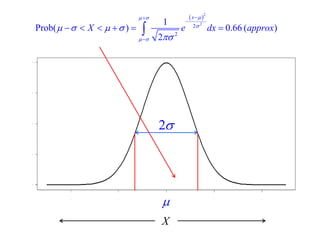
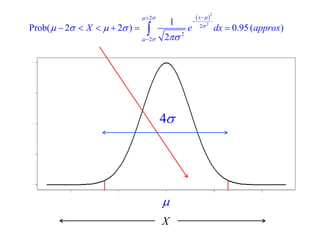
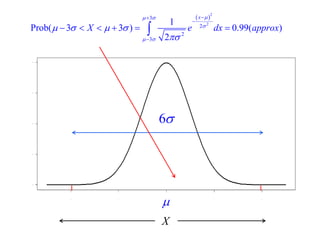
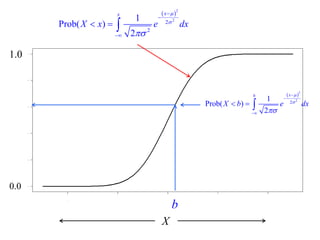
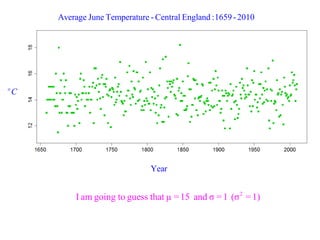
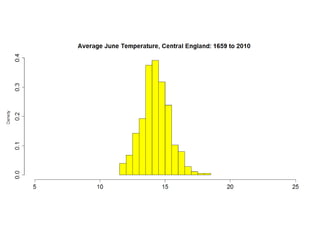
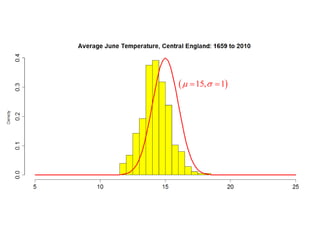
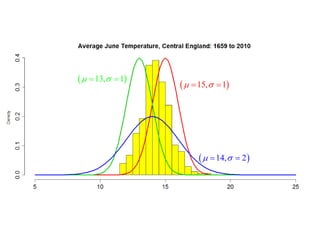
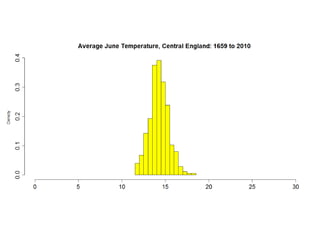
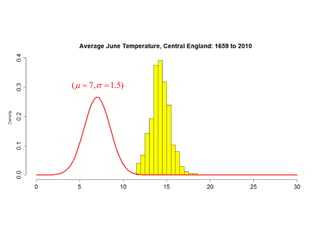
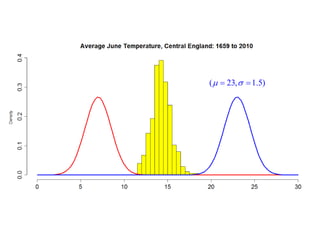
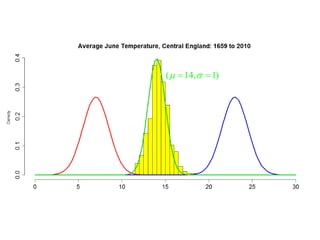
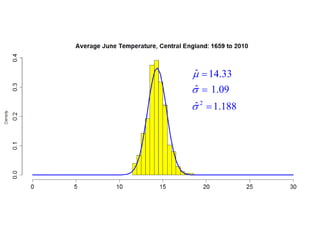
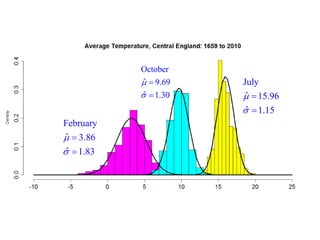
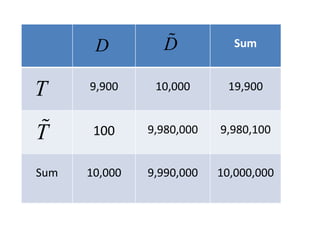
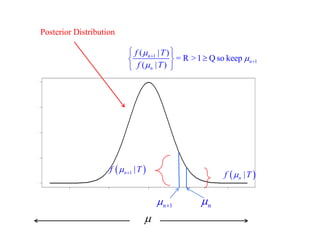
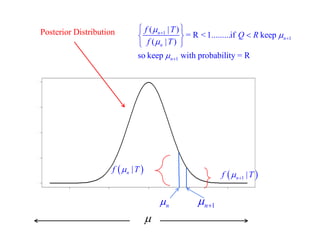
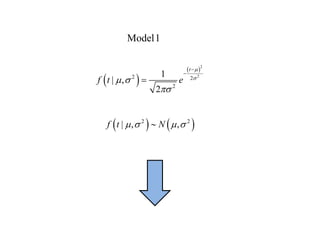
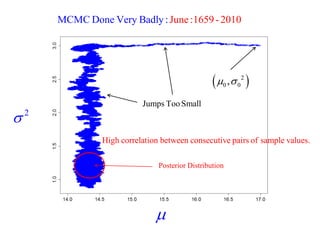
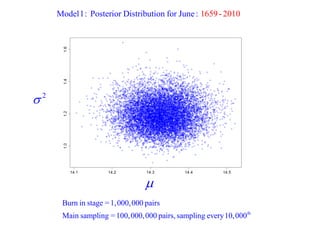
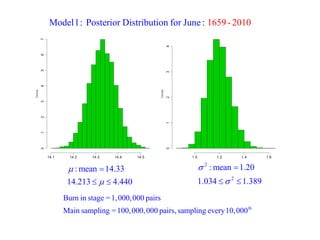
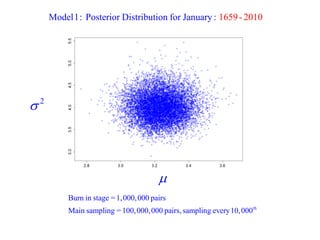
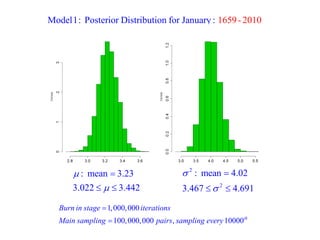
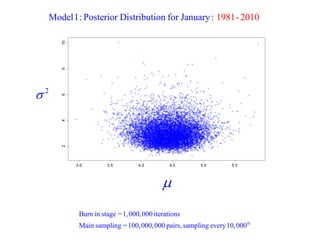
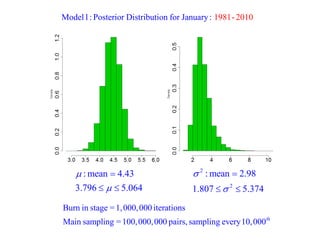
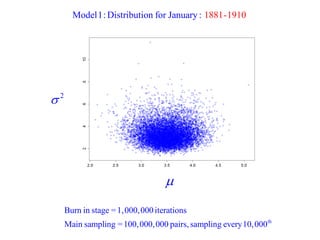
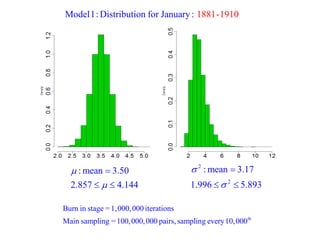
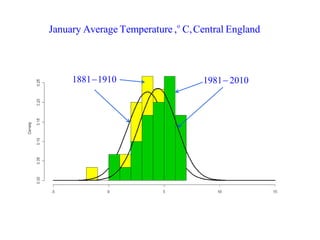
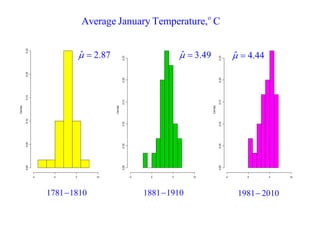
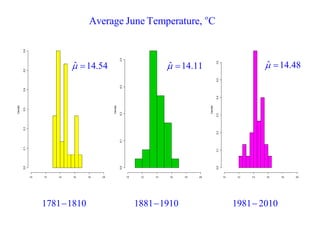
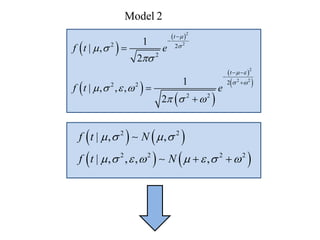
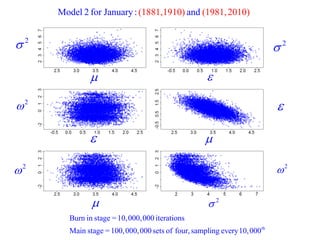
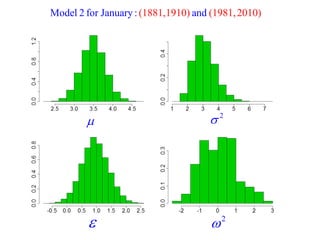
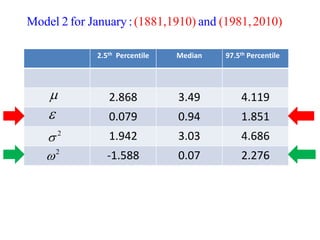
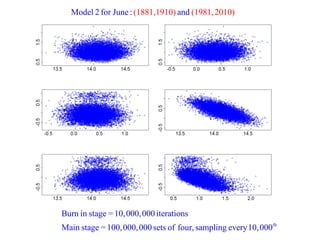
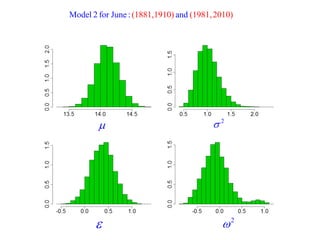
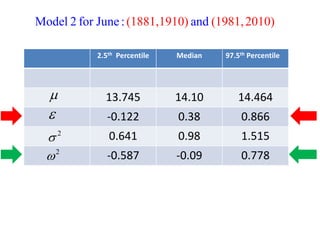
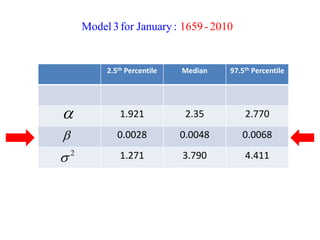
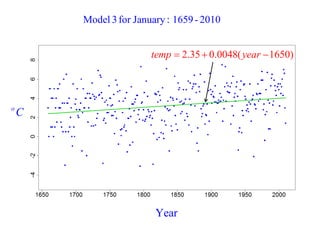
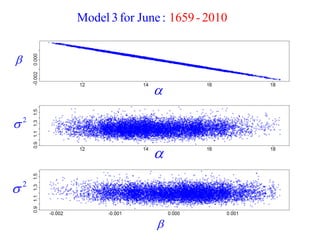
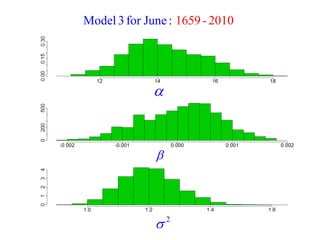
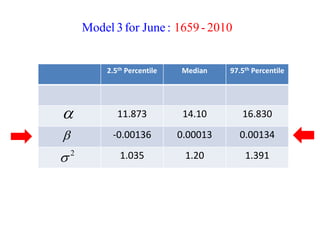
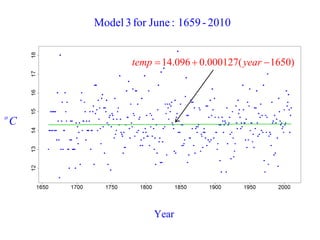
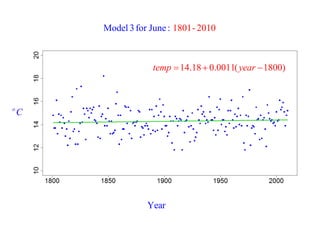
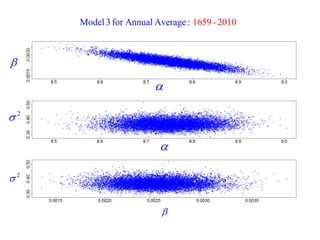
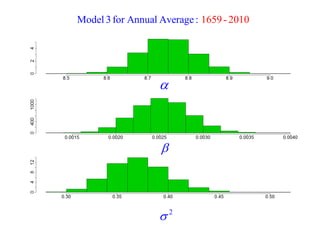
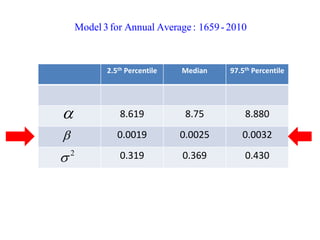
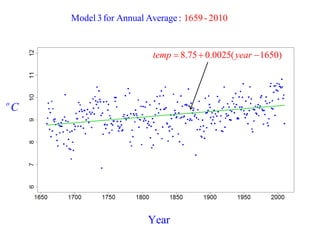
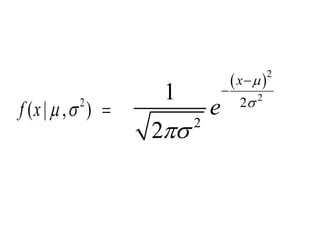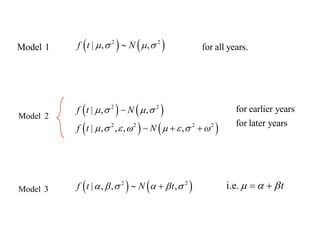This document summarizes Peter Chapman's presentation on Bayesian inference to the Wokingham U3A Maths Group. It provides biographical details on Peter Chapman, including his educational and professional background. It then explains that the motivation for the presentation was to share his new learning about Bayesian methods and the software R with the group, after taking on a contract requiring him to use these. The presentation uses temperature data from Central England between 1659-2010 to illustrate Bayesian methodology, but is not about climate change specifically.

1. My Adventures with Bayes
Peter Chapman
Wokingham U3A Maths Group
6 April 2011

2. Contents
•My background
•Motivation
•Some data
•The normal distribution
•Classical inference
•Bayes theorem
•Who was Thomas Bayes
•Bayesian inference
•Some examples of Bayesian inference

3. WHO AM I

4. CV
1962-1969: Ashford Grammar School (Middlesex/ Surrey).
A-level in Pure Maths, Applied Maths, Chemistry, Physics.
1969-1972: Manchester University - Pure and Applied Maths.
1973: Department of Education, London – Assistant Statistician.
1973-1977: Exeter University – PhD in Applied Statistics
1977-1982: Grassland Research Institute, Hurley – Statistician.
1982-2007: ICI/Zeneca/AstraZeneca/Syngenta, Bracknell - Statistician.
2007-2009: Unilever, Sharnbrook, Bedfordshire.
2009: Retired – joined Wokingham U3A – some consultancy

5. MOTIVATION

6. In September 2010 I was offered a contract by my former employer, Syngenta, of Bracknell.
The contract on offer required me to (a) carry out a Bayesian analysis, and (b) use the freeware software R. Both of these were new to me and required a significant amount of learning.
About the same time I was asked to make a presentation to the Wokingham U3A Maths Group. Since I was putting in a significant amount of time to learn new techniques, it seemed only appropriate to share this learning with them.

7. This is a presentation about Bayesian methods. Although I am using UK temperature records to illustrate methods, this is not a presentation about climate change.
A much more thorough analysis is necessary before we can say anything substantial about climate change.
This presentation is not about the normal distribution. Because the normal distribution is well known and easy to work with I have used it to demonstrate Bayesian methodology. The ideas presented here will translate to other, more complex, distributions.

8. SOME DATA

9. Monthly mean, Central England temperature (degrees C) 1659-1973 Manley (Q.J.R.Meterol.Soc., 1974)
1974-onwards Parker et al. (Int.J.Clim., 1992)
Parker and Horton (Int.J.Clim., 2005)
Year
oC
Average January Temperature - Central England :1659 - 2010
http://www.metoffice.gov.uk/hadobs/hadcet/cetml1659on.dat

10. Monthly mean, Central England temperature (degrees C) 1659-1973 Manley (Q.J.R.Meterol.Soc., 1974)
1974-onwards Parker et al. (Int.J.Clim., 1992)
Parker and Horton (Int.J.Clim., 2005)
Year
oC
Average June Temperature - Central England :1659 - 2010

11. Monthly mean, Central England temperature (degrees C) 1659-1973 Manley (Q.J.R.Meterol.Soc., 1974)
1974-onwards Parker et al. (Int.J.Clim., 1992)
Parker and Horton (Int.J.Clim., 2005)
Year
oC
Average Annual Temperature - Central England :1659 - 2010

14. Average Monthly Temperature - Central England :1659 - 2010
January
June
Annual

15. THE NORMAL DISTRIBUTION

16.  2
2 2
2
1
2
x
e





f (x | ,  2 ) 

17. 
 
 2
2 2 2
2
1
| ,
2
x
y f x e

  



 
X

2
is called the mean
is called the variance
is called the standard deviation




18. 
 2
2 2
2
1
Prob( )
2
b x
X b e dx






  
X
b


19. 

 2
2
2
2
1 2
2
1
1
Prob( )
2
b x
b
b X b e dx





   
X
b1 b2

20. 

 2
2 2
2
1
Prob( ) 1
2
x
X e dx



 


      
X

21. 2

 2
2 2
2
1
Prob( ) 0.66 ( )
2
x
X e dx approx
  

 
   

 


      
X

22. 4

 2
2
2
2
2
2
1
Prob( 2 2 ) 0.95 ( )
2
x
X e dx approx
  

 
   

 


      
X

23. 6

 2
2
3
2
2
3
1
Prob( 3 3 ) 0.99( )
2
x
X e dx approx
  

 
   

 


      
X

24.  2
2 2
2
1
Prob( )
2
x x
X x e dx






  
1.0
0.0
b
 2
2 2 1
Prob( )
2
b x
X b e dx






  
X

25.  
 2
2
x-μ
-
2 2σ
2
(Probability)
1
f x | μ,σ = e is called a Density F .
2πσ
unction (PDF)
 2
2 2 2
2
1
( | , ) is called a Cumulative Distribution Funcion ( .
2
CDF)
x x
F x e dx

  




 
2 Vertical line indicates a distribution of x conditional on the values of μ and σ

26. CLASSICAL INFERENCE

27. We have some data..............and we believe that the data derives from
a normal distribution.
Fundamental principle : the parameters, μ and σ in our case,
are fixed or constant.
.
Our objective is therefore to estimate μ and σ2............μˆ and2 σˆ .
We also want to know how precise the parameter estimates are........
.......... so we need to compute confidence intervals.
2
2 2
At this stage we can compute ( | , )for a variety of values
of μ and σ , but we do not know the correct values for μ and σ .
f x  

28. Year
oC
Average June Temperature - Central England :1659 - 2010
2 I am going to guess that μ = 15 and σ = 1 (σ = 1)

30. 15,1

31.  15, 1
 13, 1
 14,  2

32.  2
2
i
-
-
2 22
2
We have 352 values of temperature, t ,where i =1659 to 2010.
1
We can compute ( | , ) for any value of and we like.
2
ti
i f t e

    


2010
2
1659
2
i In the classical approach we compute ( | , ) for all t , i =1659 2010.
then multiply then together ( | , ) ( | , ). i
i
i
L
f t
t   f t 
 



 
This is called the likelihood.
2 We then find the values of  and  that maximise the likelihood.
2 We call these maximum- likelihood estimates : ˆ and ˆ .

34. (7,1.5)

35. (23,1.5)

36. (14,1)

37.  2
2
2010
2 2
2
1659
1
( , )
2
ti
i
L e

  




 
 
2010
* 2 2 2
2
1659
352 352 1
( , ) log (2 ) log ( ) ( )
2 2 2 e e e i
i
L Log L     t 
 
      
* 2010
2
2
1659
1
( - ) 0 i
i
L
t 
  

 
 
2010
1659
1
ˆ
352 i
i
 t t

  
* 2010
2
2 2 4
1659
352 1 1
( - ) 0
2 2 i
i
L
t 
   

   
 
2010
2 2
1659
1
ˆ ( - )
352 i
i
 t t

 

38. 2 ˆ14.33 ˆ 1.09 ˆ1.188      

39. July
ˆ 15.96
ˆ 1.15




February
ˆ 3.86
ˆ 1.83




October
ˆ 9.69
ˆ 1.30





40. Confidence Intervals
Beyond the scope of this talk

41. BAYES THEOREM

42. Q = set of people tested for disease
D = subset of people who have disease
D = subset of people who do not have disease
T = subset of people who test positive
T = set of people who do not test positive
D+D = T + T = Q
P(D) = probability that an individual has the disease
P(D| T) = probability that an individual has a disease given that they have tested positive
P(T) = probability that an individual tests positive
P(T | D) = probability that an individual tests positive given that they have the disease
( | ) ( )
( | )
( )
P T D P D
P D T
P T
Bayes Theorem: 

43. Sum
9,900
10,000
19,900
100
9,980,000
9,980,100
Sum
10,000
9,990,000
10,000,000
D D
T
T

44. 9,900 10000 19,900
100 9,980,000 9,980,100
10,000 9,990,000 10,000,000
D D
T
T
10000
( ) 0.001
10000000
P D  
19900
( ) 0.00199
10000000
P T  
( ) and ( P T P D) are marginal probabilities

45. 9,900 10000 19,900
100 9,980,000 9,980,100
10,000 9,990,000 10,000,000
D D
T
T
9900
( | ) 0.99
10000
P T D  
P(D| T) are P(T | D) are
conditional probabilities
( | ) ( )
( | )
( )
P T D P D
P D T
P T

0.99*0.001
0.00199

0.00099
0.00199

9900
19900
  0.497487
9900
( | ) 0.497487
19900
P D T  

46. BAYESIAN INFERENCE

47. A fundamental assumption of Bayesian inference is that the unknown parameters are variables.
2 For the normal distribution this means that μ and σ are variables, not constants.
2 2
2 2 2
If we apply Bayes theorem to the normal density function we get :
( | , ) ( , )
( , | ) ( | , ) ( , )
( )
L t f
f t L t f
f t
   
       
Posterior
Distribution
Likelihood Prior
Distribution
Data

48. For many years Bayesian analysis was a theoretical academic pastime.
This was because the mathematics was very difficult.
Analytic solutions for the posterior often involved complex multiple integrals.
One of the few that can be solved is the normal distribution with uniform priors.
2010
,
1659
1
352 i
i
t t

 
 
 
2010
2 2
1659
1
, - .
352 -1) i
i
and s t t

 
In what follows :

49. If μ and logσ follow independent uniform prior distributions, then :
2
2
1
f (, ) , so


     2
2 2
2
352
1 1
exp 352 1 352 ,
2
1
s t
  

           
 
 
 

   
2010
2
3 2 2
1 59
5 2
6
1 1
e
2
p ,
1
x i
i
t 
   
   
   

 
   


 
 

 
2010
2
2
16
2
59
1 1
ex ,
2
1
p i
i
t 
   
   
   
   

 
 
 

2 2 2 f (, |T)  L(T |, ) f (, )
      2
352 2
2
2 2
1
exp 35
1 1
exp 352 2
1
2
,
2
1 s t
 

 
    
 
     
 



 

 
   
 
    2
352 2
2
2
1 1
exp 352 1 ,
2 352
1
s N t ,


 
 
   

  


 






50.     2 2 2
:
( , | ) | , | ,
We need to factorise the posterior as follows
f   T  f   T  f  T
and it can be shown that that :
2
2 | , , ,
352
T N t

 
 
 
 
2 2 2  |T Inv (352 1, s ), and
2
1 | , .
352 n
s
 T t t 
 
 
 
Marginal posterior for μ
2 Marginal posterior for σ
Conditional posterior for 
2 2 f ( |T) f ( , |T)d

     
2
2 2 f ( |T) f ( , |T)d

     

51. MARKOV CHAIN MONTE-CARLO AND THE METROPOLIS METHOD

52. 2 2
2 2 2
Set up the Bayesian posterior :
( | , ) ( , )
( , | ) ( | , )
(
( , )
)
L
L T f
f T
f
T f
y
  
  

    
  2
2010
2
2
1659
In our case it takes the following form:
1 1
exp
2
1
, i
i
t 
   
   
   
 
 

 



53. 2 2
0 0 Select initial values,  and  , for  and  .
2 2
0 1 0 1 Introduce jump functions :  and  
2
1 1
2
0 0
( , | )
Compute = R.
( , | )
f T
f T
 
 
 
 
 
Sample a single random value Q from a UnifoUrm distribution (0,1)
2 2 2
1 1 1 1 0 0 If Q  min(1, R) keep ( , ) else ............( , ) ( , )
2 2 2
0 0 1 1 2 2
2 2 2
1 1
Continue doing this ( , ) ( , ) ( , )
( , ) ( , ) ( , ) n n n n big big
     
       
  
  
This results in a random joint sample from the posterior distribution.

54. 
Posterior Distribution
n 1 n  
  1 | n f  T   |  n f  T
1
1
( | )
= R >1 Q so keep
( | )
n
n
n
f T
f T





 
  
 

55. 
Posterior Distribution
n 1  n  
 |  n f  T
  1 | n f  T 
1
1
1
( | )
= R <1.........if keep
( | )
so keep with probability = R
n
n
n
n
f T
Q R
f T







 
  
 

56.   2 , n n  
  2
1 1 , n n     Jump Function
2
n 1 n rnorm(0, Z )   
2 2 2
1 (0, ) n n W   rnorm    

57. A COMPARISON OF THREE MODELS

58.  
 
 
 
 
 
2
2
2
2 2
2 2
2
2 2 2
2 2
1
| ,
2
1
| , , ,
2
t
t
f t e
f t e


 
 
 

   
  


 





 
 2
2 2 2
2
1
| ,
2
t
f t e

  



Model 1  for all years.
Model 2
for earlier years
for later years
Model 3  
  2
2 2 2
2
1
| , ,
2
t t
f t e
 
   

 


i.e.    t

59.    
   
2 2
2 2 2 2
| , ,
| , , , ,
f t N
f t N
   
       
    2 2 Model 1 f t |,  N , for all years.
Model 2
for earlier years
for later years
Model 3     2 2 f t | , ,  N   t, i.e.    t

60. for earlier years
for later years
   
   
2 2
2 2 2 2
| , ,
| , , , ,
f t N
f t N
   
       
Model 2
for earlier years
for later years
   
   
2 2
2 2
| , ,
| , ,
early early early early
late late late late
f t N
f t N
   
   
Model 2
Is the same as
2 2 2 where and late early late early       

61. Model 1
 
 2
2 2 2
2
1
| ,
2
t
f t e

  




    2 2 f t |,  N ,

62. 
2 
MCMC Done Very Badly : June : 1659 - 2010
  2
0 0  ,
Jumps Too Small
High correlation between consecutive pairs of sample values.
Posterior Distribution

63. Solution
    2 2
Better starting values 0 , 0  maximum likelihood estimates ˆ ,ˆ
Burn in sampling phase that is discarded
Main phase with infrequent sampling - e.g. every 10,000 pair th

64. 2 
th
Burn in stage =1,000,000 pairs
Main sampling =100,000,000 pairs, sampling every 10,000

Model 1: Posterior Distribution for June : 1659 - 2010

65. th
Burn in stage =1,000,000 pairs
Main sampling =100,000,000 pairs, sampling every 10,000
Model 1: Posterior Distribution for June : 1659 - 2010
:mean 14.33
14.213 4.440



 
2
2
:mean 1.20
1.034 1.389



 

66. 2 
th
Burn in stage =1,000,000 pairs
Main sampling =100,000,000 pairs, sampling every 10,000
Model 1: Posterior Distribution for January : 1659 - 2010


67. Model 1: Posterior Distribution for January : 1659 - 2010
1,000,000
100,000,000 , 10000th
Burn in stage iterations
Main sampling pairs sampling every


2
2
: mean 4.02
3.467 4.691



 
: mean 3.23
3.022 3.442



 

68. Model 1: Posterior Distribution for January : 1981- 2010
th
Burn in stage =1,000,000 iterations
Main sampling =100,000,000 pairs, sampling every 10,000

2 

69. th
Burn in stage =1,000,000 iterations
Main sampling =100,000,000 pairs, sampling every 10,000
Model 1: Posterior Distribution for January : 1981- 2010
:mean 4.43
3.796 5.064



 
2
2
:mean 2.98
1.807 5.374



 

70. Model 1:Distribution for January : 1881-1910
th
Burn in stage =1,000,000 iterations
Main sampling =100,000,000 pairs, sampling every 10,000

2 

71. th
Burn in stage =1,000,000 iterations
Main sampling =100,000,000 pairs, sampling every 10,000
Model 1:Distribution for January : 1881-1910
:mean 3.50
2.857 4.144



 
2
2
:mean 3.17
1.996 5.893



 

72. o January Average Temperature , C,Central England
18811910 1981 2010

73. o Average January Temperature, C
17811810 18811910 1981 2010
ˆ  2.87 ˆ  3.49 ˆ  4.44

74. o Average June Temperature, C
17811810 18811910 1981 2010
ˆ 14.54 ˆ 14.11 ˆ 14.48

75. Model 2
   
   
2 2
2 2 2 2
| , ,
| , , , ,
f t N
f t N
   
       
 
 
 
 
 
 
2
2
2
2 2
2 2
2
2 2 2
2 2
1
| ,
2
1
| , , ,
2
t
t
f t e
f t e


 
 
 

   
  


 






76. th
Burn in stage =10,000,000 iterations
Main stage =100,000,000 sets of four, sampling every 10,000
Model 2 for January : (1881,1910) and (1981,2010)



2 
2 
2 


 2 
2  2 

77. Model 2 for January : (1881,1910) and (1981,2010)
 2 
2  

78. 2.5th Percentile Median 97.5th Percentile
2.868 3.49 4.119
0.079 0.94 1.851
1.942 3.03 4.686
-1.588 0.07 2.276


2 
2 
Model 2 for January : (1881,1910) and (1981,2010)

79. th
Burn in stage =10,000,000 iterations
Main stage =100,000,000 sets of four, sampling every 10,000
Model 2 for June : (1881,1910) and (1981,2010)

80. Model 2 for June : (1881,1910) and (1981,2010)
 2 
 2 

81. 2.5th Percentile Median 97.5th Percentile
13.745 14.10 14.464
-0.122 0.38 0.866
0.641 0.98 1.515
-0.587 -0.09 0.778


2 
2 
Model 2 for June : (1881,1910) and (1981,2010)

82. Model 3
 
  2
2 2 2
2
1
| , ,
2
t t
f t e
 
   

 


    2 2 f t | , ,  N   t,

83. Model 3 for January : 1659 - 2010


2 

2 


84. Model 3 for January : 1659 - 2010


2 

85. 2.5th Percentile Median 97.5th Percentile
1.921 2.35 2.770
0.0028 0.0048 0.0068
1.271 3.790 4.411
Model 3 for January : 1659 - 2010


2 

86. Model 3 for January : 1659 - 2010
oC
Year
temp  2.35  0.0048( year 1650)

87. Model 3 for June : 1659 - 2010




2 
2 

88. Model 3 for June : 1659 - 2010


2 

89. 2.5th Percentile Median 97.5th Percentile
11.873 14.10 16.830
-0.00136 0.00013 0.00134
1.035 1.20 1.391
Model 3 for June : 1659 - 2010


2 

90. Year
Model 3 for June : 1659 - 2010
oC
temp 14.096  0.000127( year 1650)

91. Model 3 for June : 1801- 2010
Year
oC
temp 14.18  0.0011( year 1800)

92. Model 3 for Annual Average : 1659 - 2010




2 
2 

93. 2 


Model 3 for Annual Average : 1659 - 2010

94. 2.5th Percentile Median 97.5th Percentile
8.619 8.75 8.880
0.0019 0.0025 0.0032
0.319 0.369 0.430


2 
Model 3 for Annual Average : 1659 - 2010

95. Model 3 for Annual Average : 1659 - 2010
oC
Year
temp  8.75  0.0025( year 1650)

96. THOMAS BAYES

97. Rev. Thomas Bayes (1702-1761)
His friend Richard Price edited and presented his work in 1763, after Bayes' death, as An Essay towards solving a Problem in the Doctrine of Chances.
The French mathematician Pierre-Simon Laplace reproduced and extended Bayes' results in 1774, apparently quite unaware of Bayes' work.
It is speculated that Bayes was elected as a Fellow of the Royal Society in 1742 on the strength of the Introduction to the Doctrine of Fluxions, as he is not known to have published any other mathematical works during his lifetime.
It has been suggested that Bayes' theorem, as we now call it, was discovered by Nicholas Saunderson some time before Bayes. This is disputed.

98. Comments in place of Conclusions: Bayesian Inference
•This presentation was not about the Normal distribution.
•The Normal distribution was used to illustrate the methods.
•For the problems discussed here Bayesian inference offers few advantages over classical.
•For more complex problems, Bayesian inference offers big advantages.
•Prior to 1990 or so, Bayesian inference was a partially academic subject.
•The advent of MCMC and fast computers has made Bayesian inference a significant player in the world of data analysis.
•The numbers of PhDs in statistics is small and getting smaller but most of them are absorbed in Bayesian issues.
•Bayesian approaches are now commonplace.

99. Comments: Climate Change
•This presentation was not about climate change.
•A more thorough analysis is required before we can say anything substantial about climate change.
•The results of a limited analysis so far indicate, for Central England, that summers are not getting warmer. The range of average summer temperatures that we see today is similar to that seen in the past.
•The range of average winter temperatures seems to be narrower than in the past with an absence of very cold months in recent years.
•This effect could, of course, be a result of thermometers being placed in urban areas.
•The statistically significant increase in annual average temperature may be caused may be caused by increasing average winter temperatures.