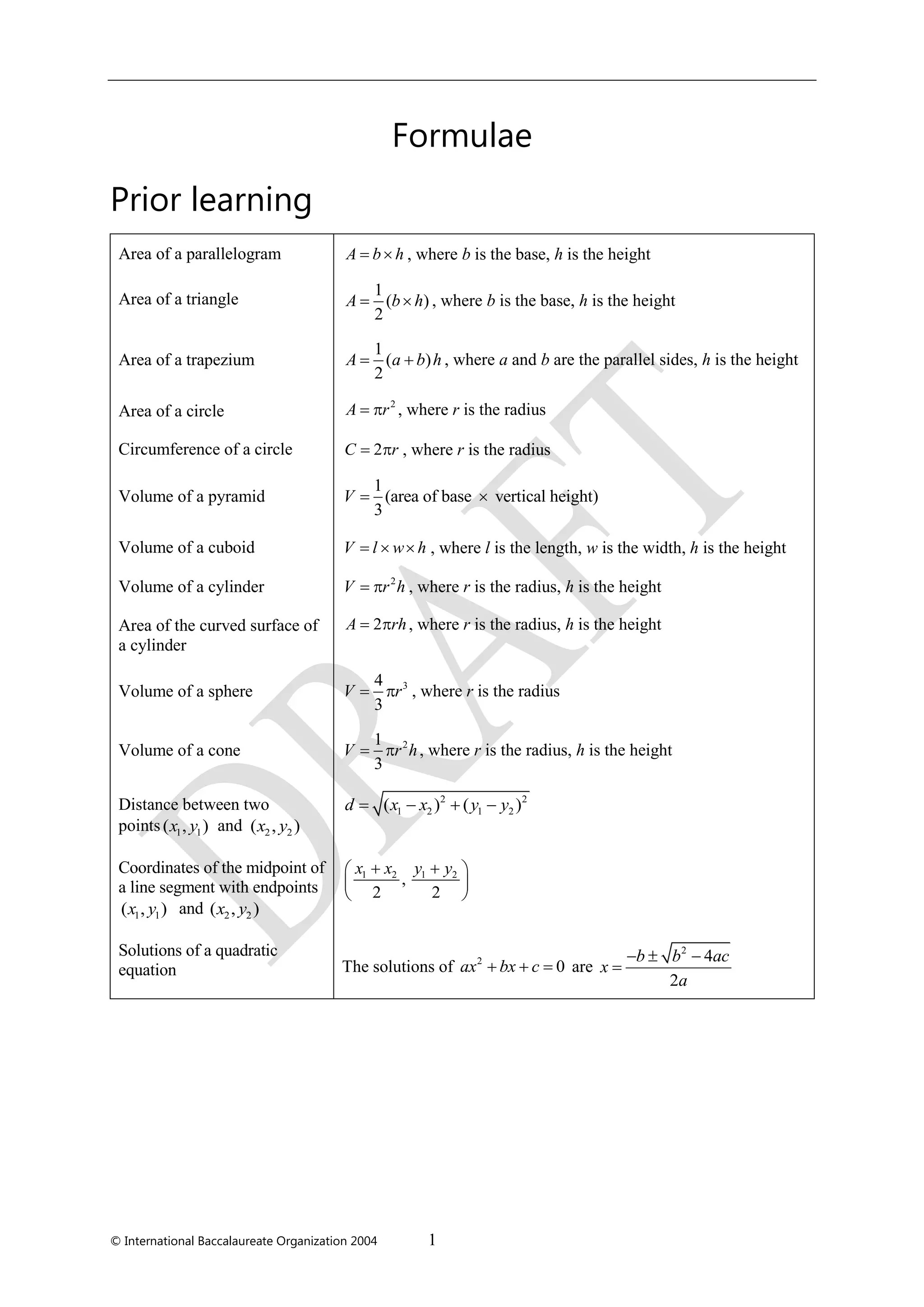
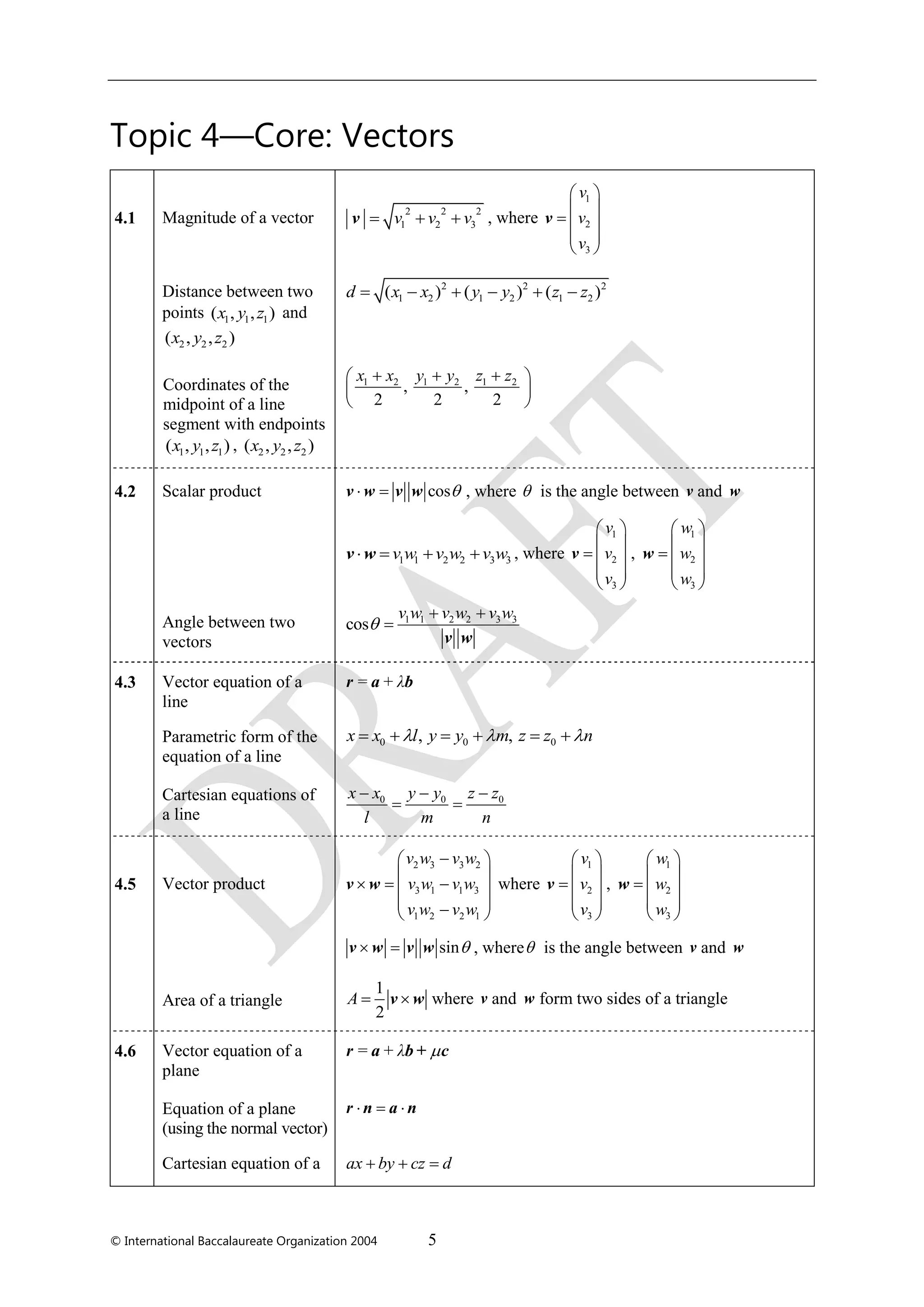
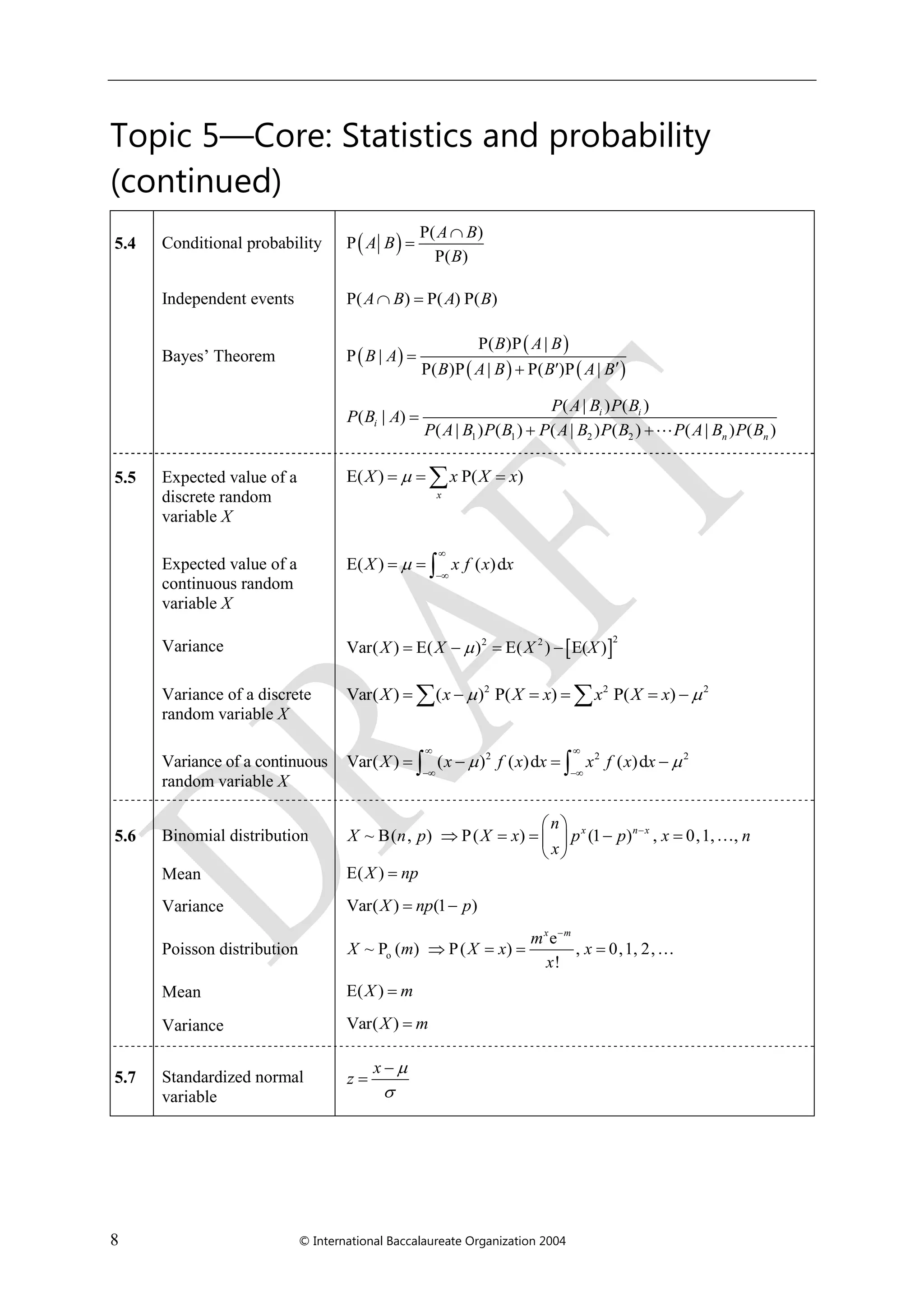
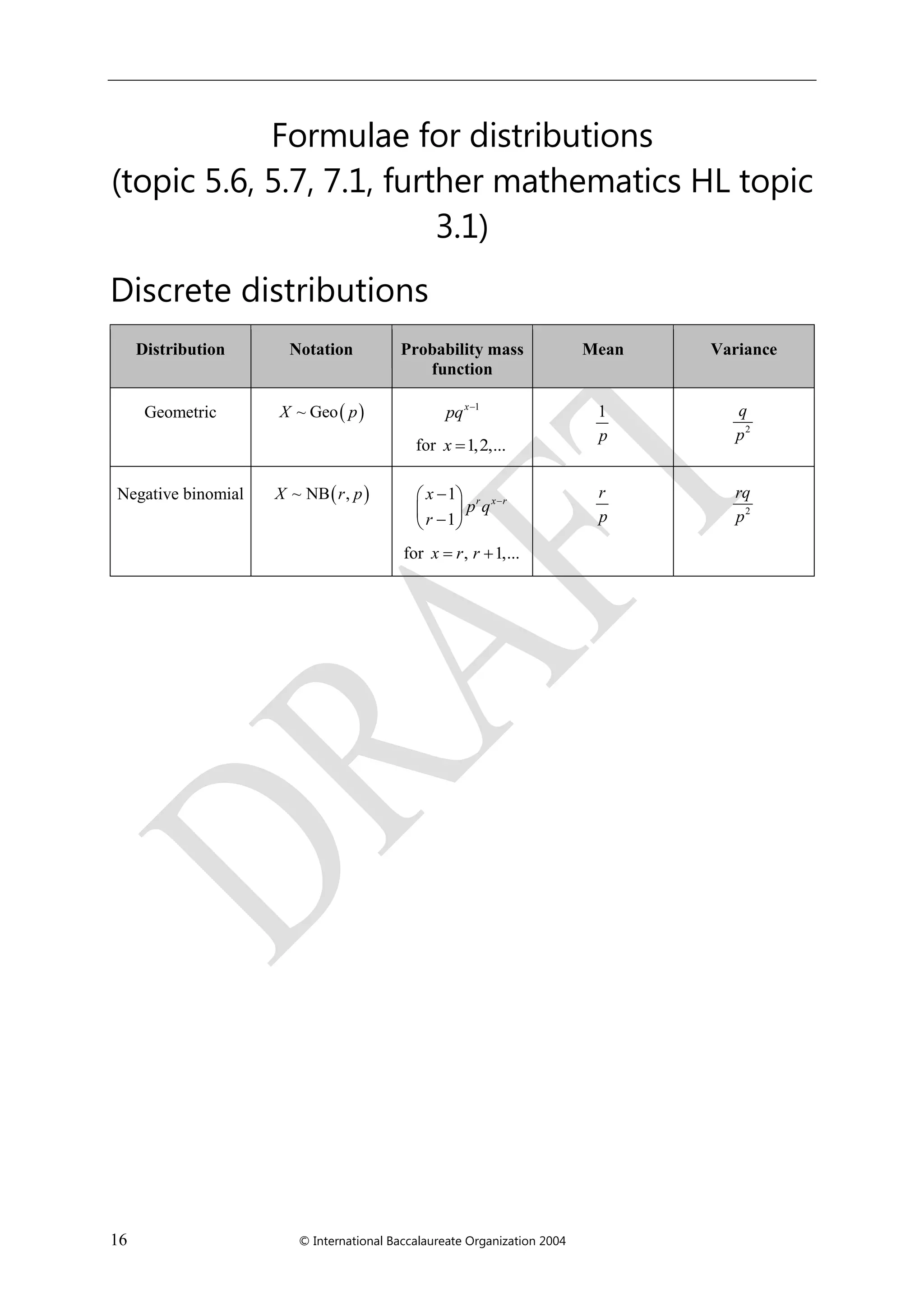
The document is a formula booklet for the International Baccalaureate's Mathematics HL and Further Mathematics HL courses. It includes essential mathematical formulas across various topics such as algebra, functions, trigonometry, statistics, probability, and calculus, intended for students during their coursework and examinations. This resource is structured into sections covering different mathematical concepts and their key formulas.