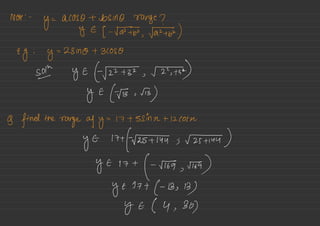Trigonometry concepts such as fundamental trigonometric ratios, important trigonometric identities, and the concept of reciprocal trigonometric ratios are discussed. Examples of solving trigonometric equations involving inverse trigonometric functions are also provided. Conversions between different angle measurement units are demonstrated along with the use of trigonometric reduction formulas.

1. Trigonometry
Abhijeet Adhikary
Notebook no :~ 2

2. Trigonometry A
fundamental Ratio
perpendicular hypotenuse
since
-_¥%%n
=
-1nsec• =
¥
=
since 01
a
B Bare
cos • =
nByp%ˢ,enme= 71 / Seco =
Irs
=
%
tano =
perpendicular
-
I /Coto =
=
#no
Base
B
important identities
① sin 20 1- COS 20 =
I [5in
'
0=2 -
COSZO
,
COP@ =
I -
sin 20 ]
② sect0 -
tanto =
1
③ correct@ -
cot 20 =
I
[
1h20 TCOPO = 1
SIMO + cosh @ = I -
25m20 .
cos 20
]
51h60 + cos 60 = 9- -
3. sin 20 .
COP@

3. concept of reciprocal
?⃝
sell 0 -
tame = 1
1sec -0 -
tano) (Seco -1 Lang ) = 2
{ 92 -
b
≥
= Ca -
b) cats )}
-
g- (Seco -1 land ) = 5
I
then
Seco -
land =
115
② cosec 20 -
co -120--1
(cosec 0 -
Coto) .
/Coleco + Coto ) =
9-
( g-
eoseeo -1*01-0--2
]
then Coleco -
Coto =
I
/z

4. g.
(seeA- 1) •
COVA =
?
[
da -
Ean ' a- = 9-
= tan 2A .
Cot
?
A
Sera -
a- =
cannot }
=
tent" ✗
¥ñA
= a- { ""
A=¥n* }
Q prove that (secotcoseco) (since + coso ) =
see 0 .
Coleco +2 .
=
#
+
¥no) ( smo + coso )
=
%÷÷•am•+|•¥mo+%%%%→
Seco .
coseco +2
=
%%%n%I
=
cone-ismy.gg?;ggso.s#ffF-so--sec0nEno=coscco]

5. B 3(Sino -
coso)
"
-161 no -10505 + 4 (sink -110560 )
⑨ 13
⑨ 10 ⑨ 5 ⑨ none
of
there
✓
AE
ut
put 0=0
310 -
1)
"
+ 6
(0+15+410+1)
= 3 + 6 + 4
= 13
Note : -
sina.am@ cold are at then put 0--00 or 90°
Y keno or to (f) nt then put 0=450
SECO >
and cosec 0--35

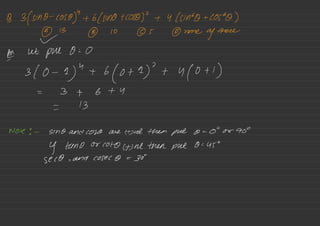
6. g find the value
of [%.tt?qanyg-
" ' n' •
] =
←put 0--480
-4¥, -1¥,
-12
:]
=
9=2--1-3-2 + I
=
¥2-1 I
=
3- ← En
ˢt
72
Q Y tano -1 Seco = 1.5.
040<90
-
the Sino =
?
Ahh , tano -1sec@ =
1.5--3/2 - ①
Ago =
1413
Seco -
tan
0=2/3 - ②
• * ""• " " • i÷%
adding both
Sino =
5)↳
AE
-2sec 0 =
%

7. 11T jam -19
⑧
snmpitysif.A-o.n.tt??I-n(A)2SecACBz2cosecA② SECA ② cose.CA
M-EE-sa-i-Y.in?---sinn-iEiEE#--
=
ˢ'ñA+;n¥%?%¥ʳ°#
=
T.IN?i::-osn--i--:..:i::;:'--s2g-A--2cosecA

8. 8kt
falu) =
# CSINKNTCOSKN),
where NER and he ≥ 9- then
f-yen ) -
f-•
In )= ?
④
ty ④1-2 ② to ⑧ 43
Ant fuln> =
1-ylsinhn-c.us"u) T
eluk
b- (sink + cos %)
=
4- ( 1- 2SMZr.com) -
% ( c- 351PM .
coin
=
ty ( 1- 2h1mn . 10PM) -1-611
-
3. sink .
core
)
=
ty
-
tfn
-
↳ +ts2n
=
4--1-6
=
¥ = ✗
try
=
II

9. 9 g- ✗ + B. =
Ia and Pty =
✗ then tana =
?
⑧ 216in B. + teeny) ⑨ tan B +
teeny ② Ian Btztany
⑧ ztanp -1
teeny
✓
let assume ✗ =p = 43° ,
y = O
'
SOI ✗ =
Is
-
B
then tana = tanui
=
2
NOW let Chellethe option which outcome will be 1
in
option ⑨ Ian Bttuny
=
tan WE + land
= I +0
=
9-

10. # Angle units
conversion
f) %
=
¥
degree f) Radian 17
2° 2
'
1
'
= 57°

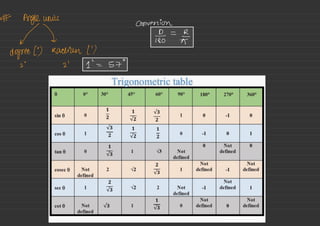
11. [90+0]>[180-0]
90°
I quadrant
-
quadrant
[ao
-0]
sin,
coseco are all ☒ ne
trice :P
ve
180
'
o
AU student take coffee
☒ quadrant ☒ quadrant I ¥ Fps ¥
(2701-07,1360-0) 9- St
tano >
101-0 -_ W Coto ,secO= ue
↓
[180+03,1270-0]
270
Reduction =
formula

12. gsinl.RO)
sin (90+30)
COS ( 1509
COS (90+60)
& tan CBS)
Lancao -145
)
=
COS 30
'
=) -
51h60 = -
Lotus
"
=
B12 -53/2 = -
9-
glanciso) 9 tonnes
=
tncao -160 ) =
ten / 180+307 (4^+1)^72
=
-
C. 0€60 = + teen 30
'
= -
Fg
=
£3
Cn
-11 )Ñ 2nA
Ossining
)
A sin /7AM
;) M -
"
%
=
-
Smitty
= -5312

13. since-03 =
-
Sino ¥
Sin C- 30) =
-
81h30
COS C-D) = COSO
= -
I / 2
tan to > = -
tano
see C- A) = Seco
cosec c- 0 ) =
-
cosec @
cot C- 03 = -
Coto
formula
sin IATB) = sina.COSB-COSA.sn B
sin /A- B) = sin A. COSB -
sin B- COSA
COSIATB
) = COSA . COSB -
SINA.SI NB
cos CA -
B) = COSA .
COSB -151nA .
Sin B
tan /ATB) =
tan A.+ tan B lancet
-
B) =
tana -
tan B
_ÑaB Élan B.

14. B Sinti ? 9 costs ?
=
Sin (450-30)
= SIN 45° .
10535 -
bin300 ,
COS 45
'
= cos 45 . cos 307 sin 45 :S /Bo
=
+
¥ :
-
fz✗Bz -
¥ ✗
±
=
En
-
Es
=
Era -1¥
=
v⇐ =%÷
2 V2
g. tank ?
= Lan / 45-30 )
←¥
=
¥÷:::::÷;÷/-¥
=
9=-1-1
:÷
.

15. § COS C- 300] •
COS 60 -1 Since -3007 . 81h60
COS 300° • COS 60° -
81hrs00 .
sin 60
'
= cos
(300+00)
= COS 360°
= 9-
Q
if A- + B. = 45°
,
then Cittern A) • Litton B) =
?
④ =0 ⑧ I
⑧2 ⑨ noneafthere
5°F
A+B=UF ,
A-
-45:B
=
[ I + tan 145-
B) ] . [ I 1- KMB] =
¥B-11 -
tomb
"
÷::::÷÷::::÷
:/
=
+1-+1%13,3×4 _i→n• ]

16. formic
1. sin ( Atb) •
Sin CA -
B) = SINZA -
SinZB
2. COS CAT B) .
COS /A -
B) =
COPA -
SIN B
3. SIN AT SMB =
2. sin
AIZB .
Cos
AIB
4. 51nA -
SMB =
2 .
Cos
A¥ .
Sin
A
5. COSA + COS B =
2. COS
A B
◦
COS
A
6- COSA -
COS B = -
25in
c¥
.
sin
¥0

17. B.
917*5%1%-4 0=+13 029-0--7.5 >
then final
ˢ%?%_%¥→= ?
SOI 2 COS
(70%500) ◦
sm(7÷s•)
=
2 cos /
700¥00
)
.
$0s
¥4
5ᵗʰ
2%7%-30
• Sin
(70-2-30)
2 cos
30-12-70 .
Cos
70-2-30
=
:::%ˢ
.ie?--:::#::e:::--Lan0
= tan 20
= tan 15°
-
.
tartly =
tan (45-30)
=
V3 =
ff÷,

18. formula
since =
25in 012.0592
SM20-2EfYnz@sin2O-2SlnQ.C0SOS1n4O-2S1n20.c
0520 COS 20 =
9--1*2-0
COS 20 = COSZO - SIRO
,
or 1- 25m20
2ttan20tan-O-2tY7a-n2@N0IAsinO.s
in /60-0) .
Sin /60+0) =
lysin 30
Eg . Sin 20 ✗ 51h40
'
✗ sin so
=
Lysin
3×20
=
tysln 60
'
-
-
EAT

19. 2
COS 0 .
Cos (60-0) . Cos (60-10) =
l-y.CO530
3 tan 0 .
tan (60-0) . tan (60+0) = tan 30
g find teen 6° . tank? tan 66° . Ian 78° =
?
SOI teen 6° ✗ tan 66
.
✗ tank
.
✗ Ianto
'
✗
t¥¥y.
✗
¥4,4.
am
term
internat of
tan "
i±aneÉ✗.iq#::IixIeg-I;:IIeinIiIEn
" "°
=
;÷::✗÷÷:
=
¥%:✗T%%→
=
9- ✓

20. " "
±
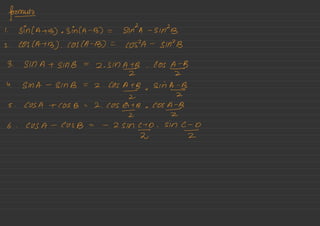
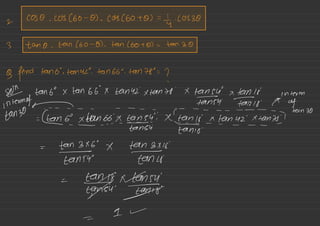
.g%E%EEn
:-
-
111050<-2
coseco> 1 or coseco≤ -2 [coseco ≠ -4-1,17]
Seco ≥ a- or Seco ≤ -2
[ see @ ≠ ¢-7,17]
-
Okano ! -10
-
0
Ufo < •
9 find the
orange af y :(Sinn -1232+1
501 =
(1-9,1)+212+9
=([ +1,379+2
=
(9- > 9) +2
=
12 ,
10)

21. Note : -
y=
acosotibsino range ?
Y C-
1- tart , Ftw)
Eg
i
g-
-281nA -13080
SOI YE (-7+32,55+32)
y c-
(FB >
Fs
)
g find the
range of y=
17 -15s inn -112 can
ye 171TEur ; Ft )
yc-i-t-f-ra.ro)
Yt 171-(-1%13)
YE ( 4,307