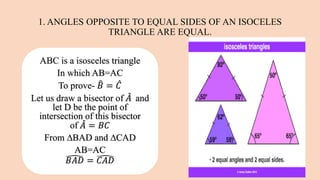
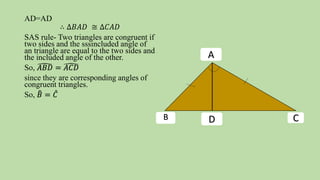
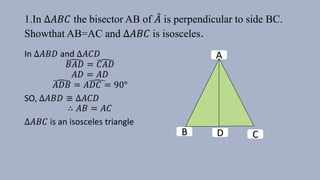
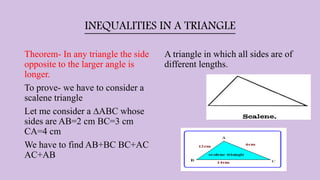
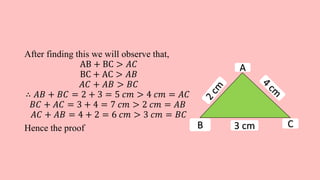
This document discusses two properties of triangles: 1. The theorem that in an isosceles triangle, the angles opposite the equal sides are also equal. This is proven using congruent triangles and corresponding angles. 2. The inequality that in any triangle, the side opposite the greater angle is longer. This is proven by considering a scalene triangle and showing the side lengths satisfy the inequality.

1. PROPERTIES OF TRIANGLE
presented by,
JYOTI S SORATUR
Roll no:60
kle’s college of education, hubli

2. CONTENTS
1.Theorem- Angles opposite to equal sides of an isoceles
triangles are equal.
2. Inequalities of a triangle
Statement- In any triangle the side of opposite to the
greater angle is longer.

4. J:Triangles _ Educational Video for
Kids - YouTube (360p).mp4

5. 1. ANGLES OPPOSITE TO EQUAL SIDES OF AN ISOCELES
TRIANGLE ARE EQUAL.
ABC is a isosceles triangle
In which AB=AC
To prove- 𝐵 = 𝐶
Let us draw a bisector of 𝐴 and
let D be the point of
intersection of this bisector
of 𝐴 = 𝐵𝐶
From ∆BAD and ∆CAD
AB=AC
𝐵𝐴𝐷 = 𝐶𝐴𝐷

6. AD=AD
∴ ∆𝐵𝐴𝐷 ≅ ∆𝐶𝐴𝐷
SAS rule- Two triangles are congruent if
two sides and the sssincluded angle of
an triangle are equal to the two sides and
the included angle of the other.
So, 𝐴𝐵𝐷 = 𝐴𝐶𝐷
since they are corresponding angles of
congruent triangles.
So, 𝐵 = 𝐶
B C
A
D

7. INEQUALITIES IN A TRIANGLE
Theorem- In any triangle the side
opposite to the larger angle is
longer.
To prove- we have to consider a
scalene triangle
Let me consider a ∆ABC whose
sides are AB=2 cm BC=3 cm
CA=4 cm
We have to find AB+BC BC+AC
AC+AB
A triangle in which all sides are of
different lengths.

8. After finding this we will observe that,
AB + BC > 𝐴𝐶
BC + AC > 𝐴𝐵
𝐴𝐶 + 𝐴𝐵 > 𝐵𝐶
∴ 𝐴𝐵 + 𝐵𝐶 = 2 + 3 = 5 𝑐𝑚 > 4 𝑐𝑚 = 𝐴𝐶
𝐵𝐶 + 𝐴𝐶 = 3 + 4 = 7 𝑐𝑚 > 2 𝑐𝑚 = 𝐴𝐵
𝐴𝐶 + 𝐴𝐵 = 4 + 2 = 6 𝑐𝑚 > 3 𝑐𝑚 = 𝐵𝐶
Hence the proof 3 cm CB
A

9. J:Triangle Inequality Theorem - Example -
YouTube (360p).mp4
J:Side opposite to greater angle is longer in
a triangle (Theorem and Proof) - YouTube
(360p).mp4

10. 1.In ∆𝐴𝐵𝐶 the bisector AB of 𝐴 is perpendicular to side BC.
Showthat AB=AC and ∆𝐴𝐵𝐶 is isosceles.
In ∆𝐴𝐵𝐷 and ∆𝐴𝐶𝐷
𝐵𝐴𝐷 = 𝐶𝐴𝐷
𝐴𝐷 = 𝐴𝐷
𝐴𝐷𝐵 = 𝐴𝐷𝐶 = 90°
SO, ∆𝐴𝐵𝐷 ≅ ∆𝐴𝐶𝐷
∴ 𝐴𝐵 = 𝐴𝐶
∆𝐴𝐵𝐶 is an isosceles triangle
A
D CB