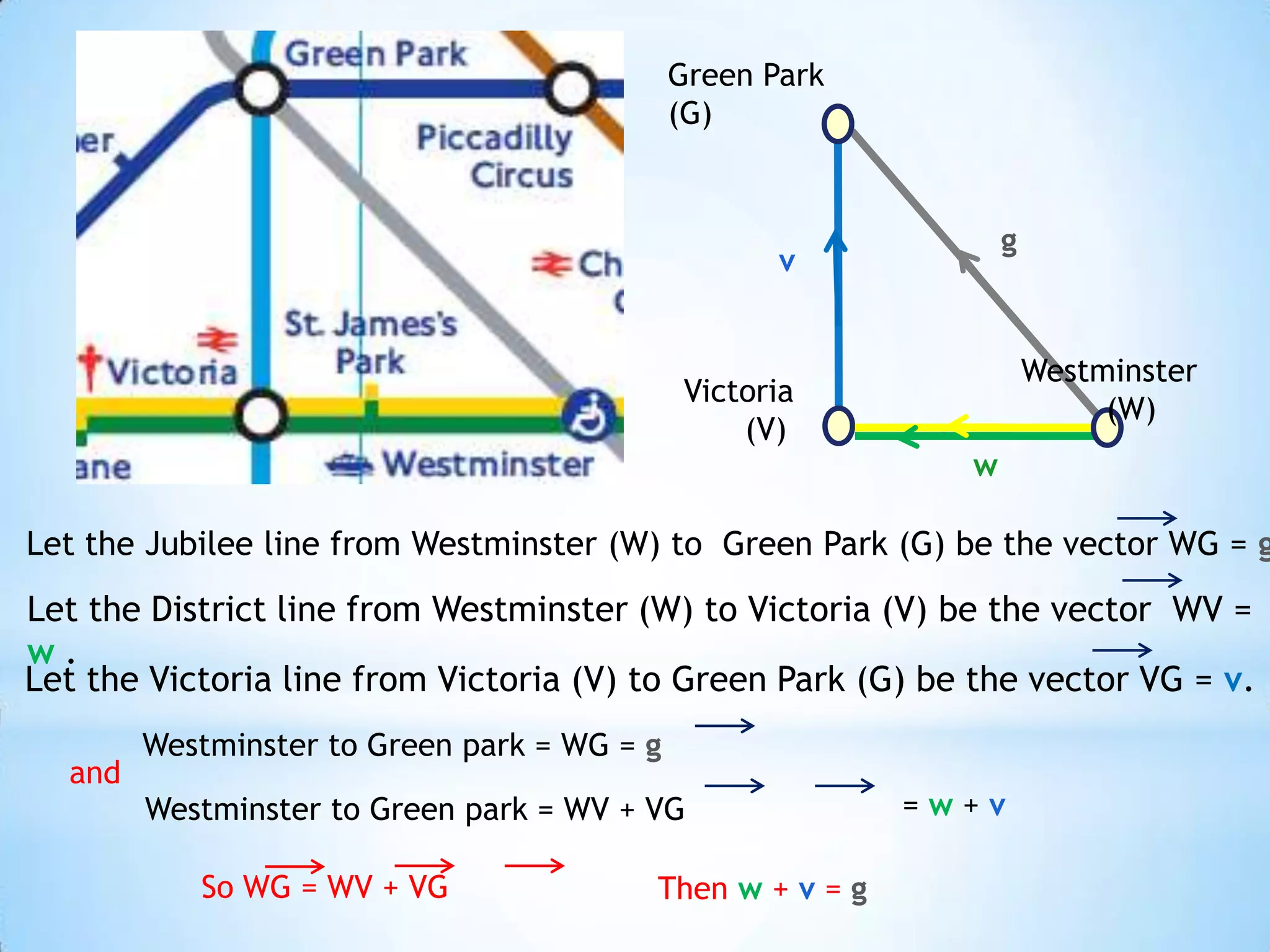
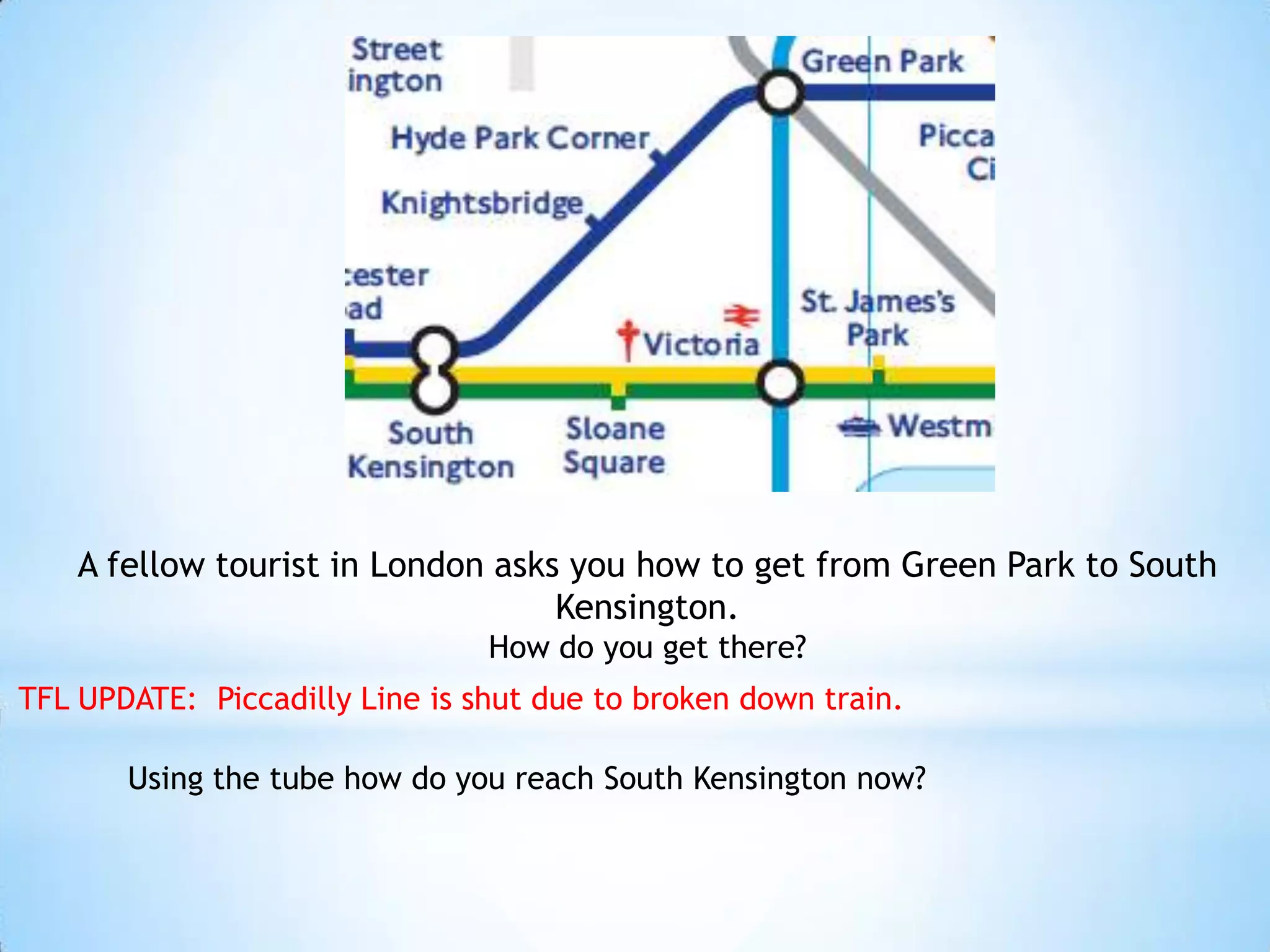
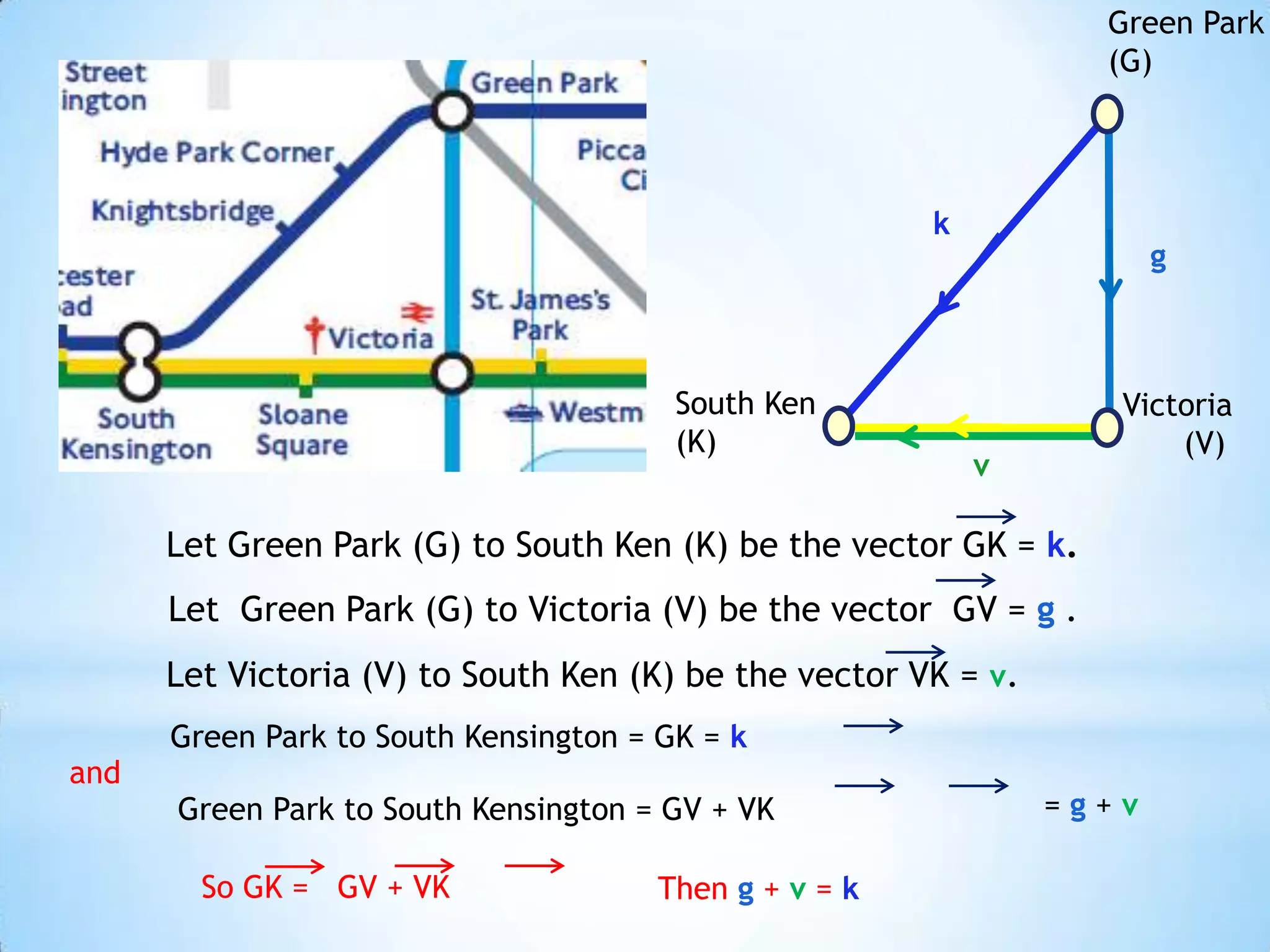
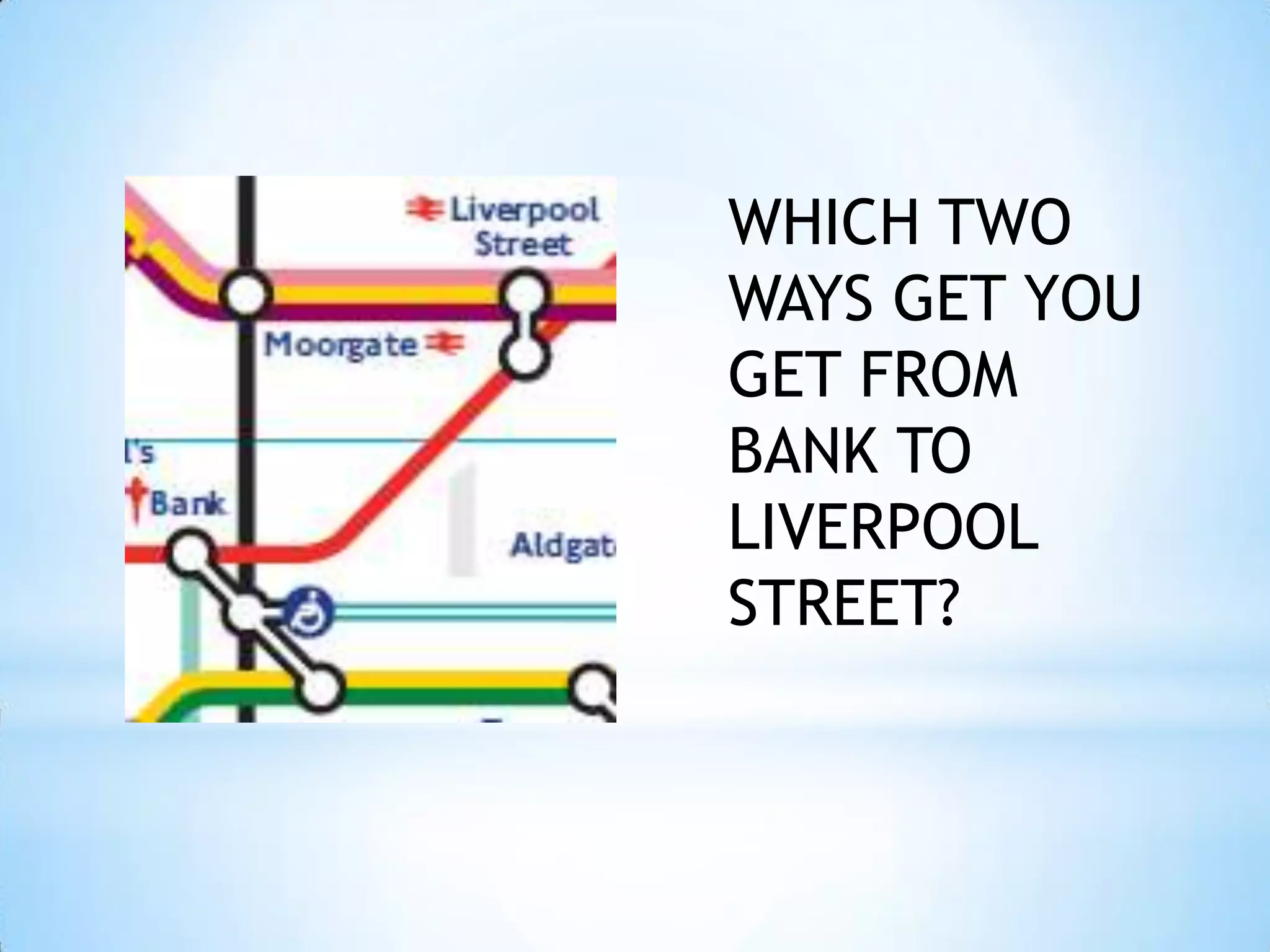
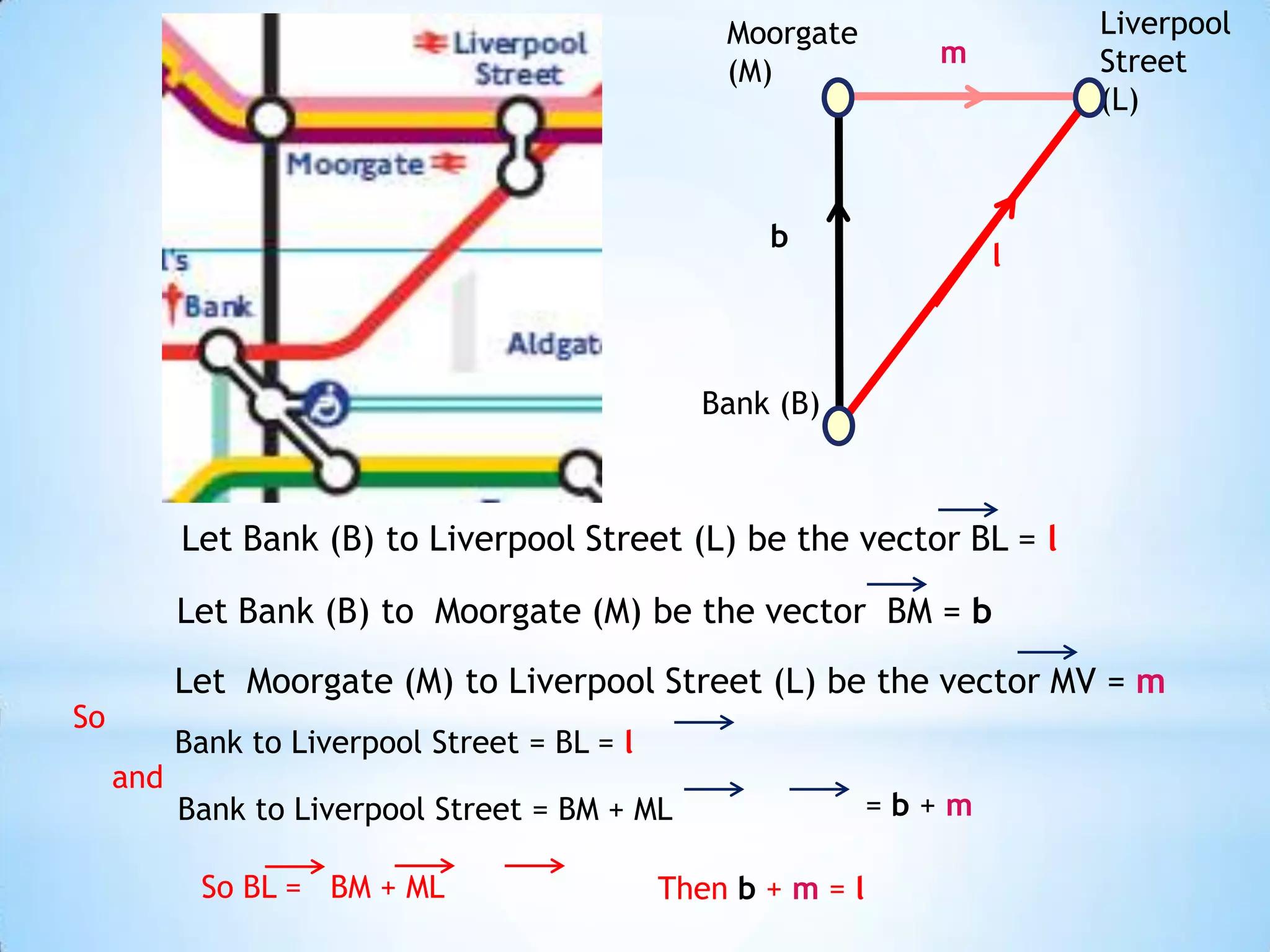
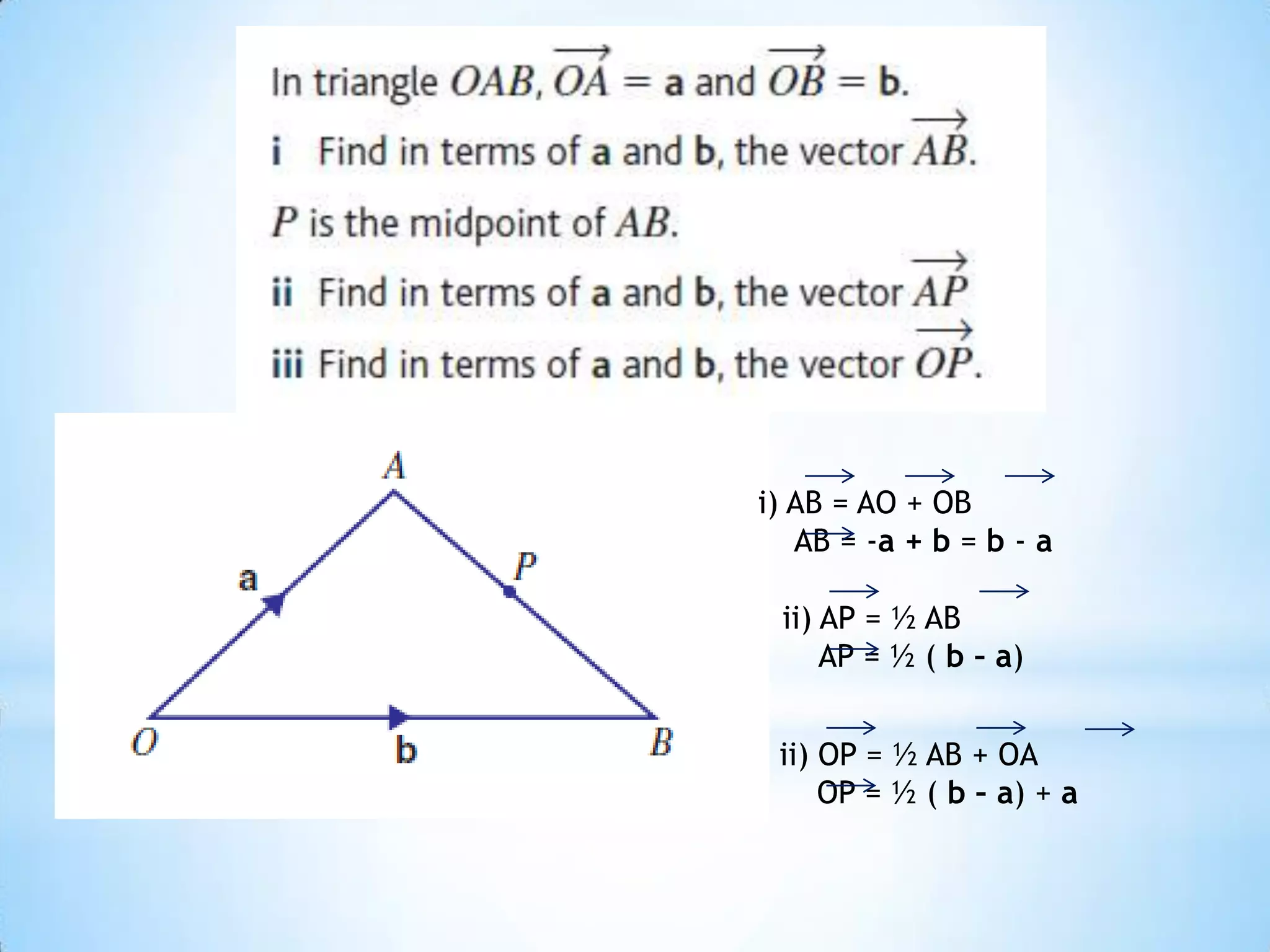
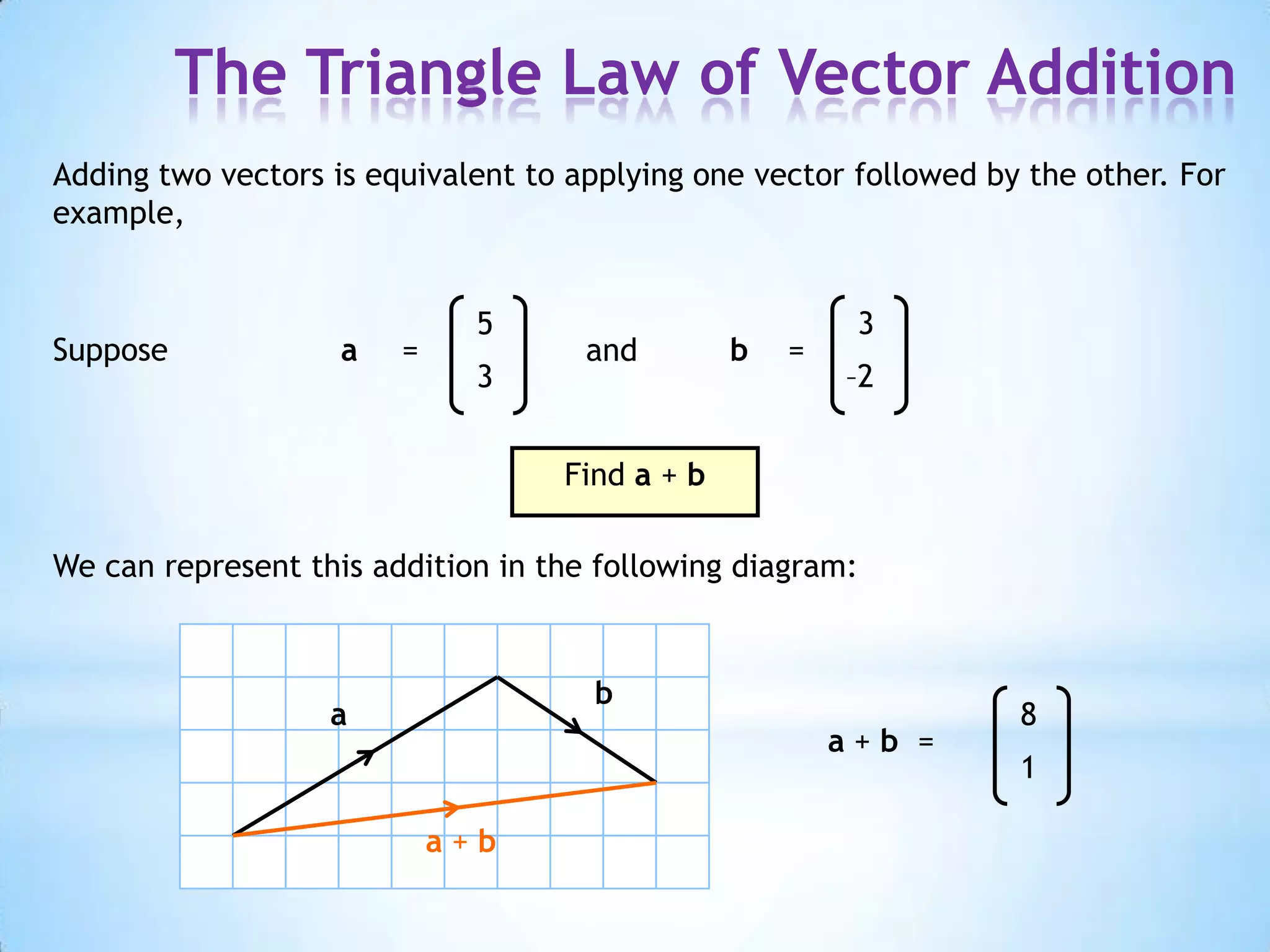
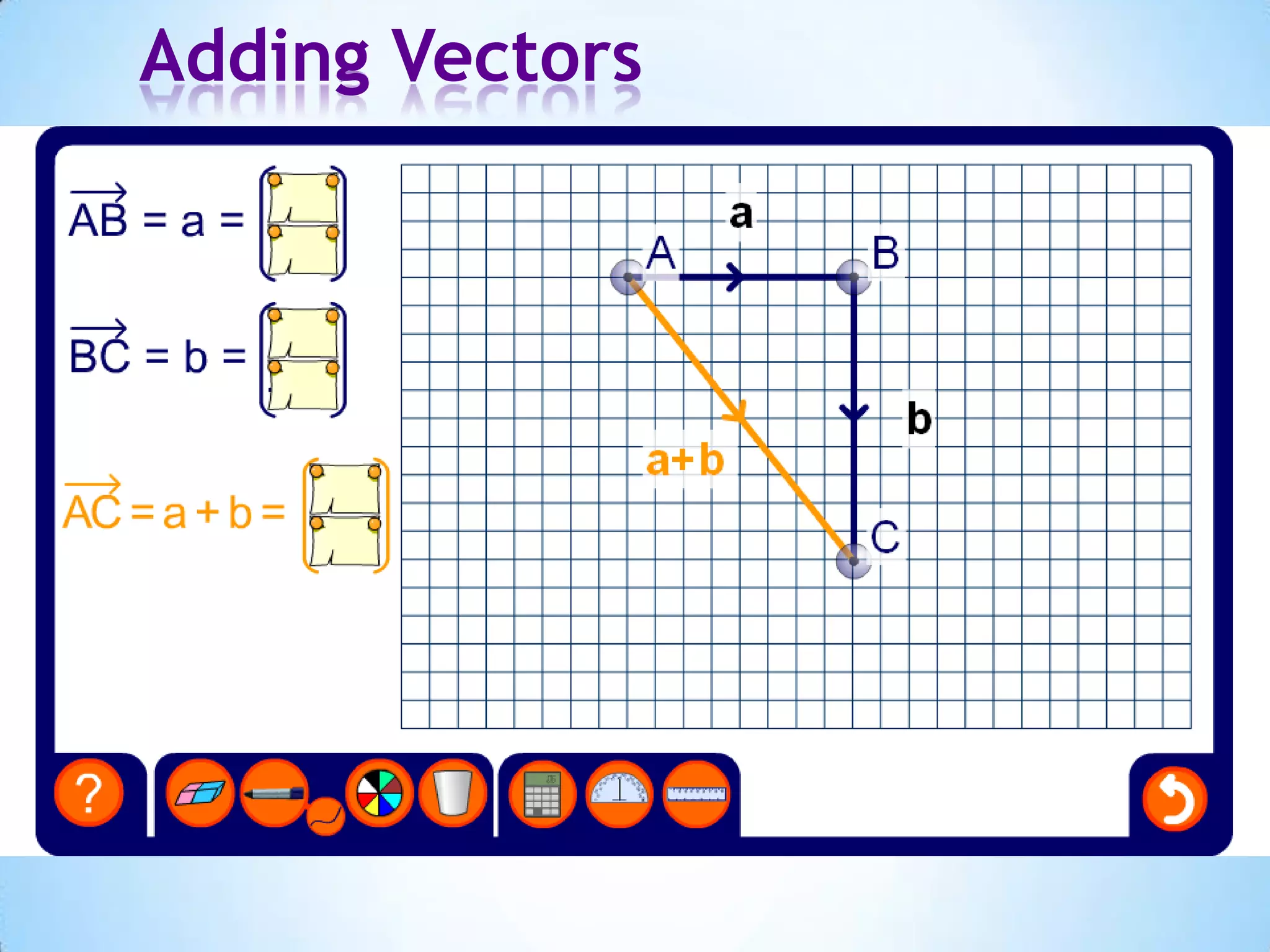
The document provides instructions for navigating the London Underground when certain lines are closed for maintenance. It explains how to get from Westminster to Green Park by taking the District Line from Westminster to Victoria and then the Victoria Line from Victoria to Green Park. Similarly, it explains how to get from Green Park to South Kensington by taking the Victoria Line from Green Park to Victoria and then the District Line from Victoria to South Kensington. Finally, it notes that there are two ways to get from Bank to Liverpool Street: taking the Central Line from Bank to Moorgate and then the Circle/Hammersmith & City lines from Moorgate to Liverpool Street, or taking the Northern Line directly from Bank to Liverpool Street.

1. You’re a tourist in London and want to travel Westminster to Green Park.How do you get there?TFL UPDATE: Jubilee Line is Down due to engineering works.Using the tube how do you reach Green Park now?

2. Green Park (G) gvWestminster (W)Victoria(V)wLet the Jubilee line from Westminster (W) to Green Park (G) be the vector WG = g.Let the District line from Westminster (W) to Victoria (V) be the vector WV = w .Let the Victoria line from Victoria (V) to Green Park (G) be the vector VG = v.Westminster to Green park = WG = gand= w+ vWestminster to Green park = WV + VGSo WG = WV + VG Then w+ v= g

3. Triangle Law of Vector AdditionBy the Triangle Law of Vector Addition: AB + BC = AC a + b = cWhenc = a + bthe vector c is said to be the RESULTANT of the two vectors a and b.

4. A fellow tourist in London asks you how to get from Green Park to South Kensington.How do you get there?TFL UPDATE: Piccadilly Line is shut due to broken down train.Using the tube how do you reach South Kensington now?

5. Green Park (G) kgSouth Ken (K)Victoria(V)vLet Green Park (G) to South Ken (K) be the vector GK = k.Let Green Park (G) to Victoria (V) be the vector GV = g .Let Victoria (V) to South Ken (K) be the vector VK = v.Green Park to South Kensington = GK = kand= g + v Green Park to South Kensington = GV + VKSo GK = GV + VK Theng+ v = k

6. WHICH TWO WAYS GET YOU GET FROM BANK TO LIVERPOOL STREET?

7. Liverpool Street (L) Moorgate (M)mblBank (B)Let Bank (B) to Liverpool Street (L) be the vector BL = lLet Bank (B) to Moorgate (M) be the vector BM = bLet Moorgate (M) to Liverpool Street (L) be the vector MV = mSo Bank to Liverpool Street = BL = land= b+ mBank to Liverpool Street = BM + MLSo BL = BM + ML Then b+ m= l

8. AD = AC + CDAD = a + b + cAC = AB + BCAC = a + b

9. i) AB = AO + OB AB = -a + b = b - aii) AP = ½ AB AP = ½ ( b – a) ii) OP = ½ AB + OA OP = ½ ( b – a) + a

10. 358Suppose a=b=and–231baa + b =a + bThe Triangle Law of Vector AdditionAdding two vectors is equivalent to applying one vector followed by the other. For example,Find a + bWe can represent this addition in the following diagram:

11. caIn general, if a=b=anddba + ca + b=b + dAdding VectorsWhen two or more vectors are added together the result is called the resultant vector.We can add two column vectors by adding the horizontal components together and adding the vertical components together.

12. Adding Vectors

13. –24Suppose andb=a=34–2644 – –2–==3144 – 3Subtracting VectorsWe can subtract two column vectors by subtracting the horizontal components and subtracting the vertical components. For example,Find a – ba – b =

14. –24andb=a=34b–b–baaa – b6a – b =1Subtracting VectorsTo show this subtraction in a diagram, we can think of a – b as a + (–b).

15. Adding and Subtracting Vectors